A HYBRID CLASSIFIER WITH GENETIC WEIGHTING

Benjam

ın Moreno-Montiel and Ren

e MacKinney-Romero

Departamento de Ingenier

ıa El

ectrica, Universidad Auton

oma Metropolitana, Iztapalapa, M

exico D.F., Mexico

Keywords:

Classiﬁcation, Data Mining, Ensemble Based System, Knowledge Discovery in Databases (KDD), Machine

Learning.

Abstract:

This paper presents the results obtained when classifying a group of artiﬁcial and real world data, using a

Hybrid Classiﬁer with Genetic Weighting (HCGW). The algorithm proposed is an ensemble based system, it

combines several types of classiﬁers: Naive Bayes, K-Means, k-Nearest Neighbours, C4.5, Decision Tables

and ADTree, using a voting criterion for weighted majority to combine the individual classiﬁcations of each

classiﬁer, assigning the weights for each classiﬁer using a genetic algorithm. We performed tests on data with

different tools for Data Mining, like SIPINA, TANAGRA and WEKA, to have a good comparison with the

proposed algorithm. Using standard measures such as accuracy, HCGW obtained better performance against

different implementations, from those tools, including traditional Ensemble Algorithms.

1 INTRODUCTION

One of the areas with a lot of interest in the last ten

years, is Data Mining, mainly due to the increase in

size of Data Bases (DB), with a resulting increase in

the potential of knowledge that lies within them. Data

Mining is an important phase in the process of Know-

ledge Discovery in Databases (KDD), performing ex-

ploration and analysis to identify nontrivial patterns

(knowledge) which are novel, potentially useful and

understandable in large DB. One of the main task

in Data Mining, is classiﬁcation, used to predict the

class of an example within the data, and performed

by means of diverse types of classiﬁers.

When performing classiﬁcation of data, we should

consider a model that allows us to classify each exam-

ple. Normally we have a data set used to build the

classiﬁcation model, this is called the training set.

In which for each example its classiﬁcation is given,

allowing us to obtain a trained model, thus enabling

us to classify new examples. These classiﬁcation mo-

dels are called classiﬁers and can be found in the lit-

erature as decision trees, decision rules, classiﬁers

based in cases, neural networks, support vector ma-

chines, among many others.

In this work we propose to perform classiﬁcation

of data using an ensemble based system. The objec-

tive of the ensemble based classiﬁers is to use several

types of classiﬁers to improve accuracy, using some

criterion to combine individual classiﬁcations. Bauer

et al.(Bauer and Kohavi, 1999), Schapire(Schapire,

2001), Quinlan(Quinlan et al., 2008) and others, con-

sider the construction of an ensemble, using weak

learners of only one kind of classiﬁers, usually deci-

sion trees, later a criterion to combine classiﬁcations

is applied, combining the individual classiﬁcations of

each weak learner, obtaining a model of classiﬁcation

with better accuracy. Kelly et. al.(Kelly and Davis,

1991), consider the construction of an ensemble, us-

ing a classiﬁer based on cases called k-nearest neigh-

bours, in which each one of the near neighbours is

weighted, using a genetic algorithm.

The algorithm we propose is called Hybrid Clas-

siﬁer with Genetic Weighting (HCGW). The HCGW

uses an ensemble based system of type Mixture of Ex-

perts and a weighted majority voting criterion to com-

bine the individual classiﬁcations of each classiﬁer,

that is to say, each classiﬁer has a different weight

according to the results of a genetic algorithm. This

algorithm provides a novel form to classiﬁcation, be-

cause it actually considers several type of classiﬁers,

and not only decision trees, as it is normally found

in the literature. It also uses a new form to assign

weights to each classiﬁer, unlike mixture of experts

neural network, using a genetic algorithm to assign

weights to each classiﬁer. The main DB used for

this paper is a real world DB, used in the discovery

challenge for the European Conference on Machine

359

Moreno-Montiel B. and MacKinney-Romero R..

A HYBRID CLASSIFIER WITH GENETIC WEIGHTING.

DOI: 10.5220/0003460003590364

In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 359-364

ISBN: 978-989-8425-77-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Learning and Principles and Practice of Knowledge

Discovery.

This paper is organised as follows. In Section 2

we will discuss previous work on ensemble based sys-

tems. In Section 3 we describe how we build the

HCGW. In Section 4 we will show the DB that was

used, so that in Section 5 the tests that were performed

to this DB and some standard data sets from the UC

Irvine repository(Frank and Asuncion, 2010), can be

discussed along with results obtained using several

tools of Data Mining. We will compare our results

with those from other tools used. We will perform a

statistical analysis to see the level of signiﬁcance of

these tests using t-Test. Finally we will present some

Conclusions and Future Work.

2 PREVIOUS WORK

There are several methods for classiﬁcation in Ma-

chine Learning, we will focus on ensemble based sys-

tems which we will review in this section:

• Bagging: Method introduced by

Breiman(Breiman, 1996), short for bootstrap

aggregating, is one of the earliest ensemble based

algorithms. This method is easy to implement,

the ensemble consists in taking a single type

of classiﬁer (usually decision trees), generating

different models of the same classiﬁer. A training

data subset is used to train a different classiﬁer

of the same type, using 75% to 100% of the size

of DB. Finally individual classiﬁcations are then

combined by taking a majority vote.

• Boosting: In the 90’s this type of ensemble

based system was developed, by work made by

Schapire(Schapire, 2001), he proved that if a

weak learner is selected, and used with diffe-

rent sets, combining their individual classiﬁca-

tions, it can be turned into a strong learner,

resulting in the Boosting Algorithm, considered

one of the seminal algorithms for Machine Lear-

ning(Polikar, 2006). The construction of the al-

gorithm is similar to the one of Bagging, a diffe-

rence being that it introduces the notion of sam-

ples with replacement for the phase of training

of weak learners. It also considers only decision

trees classiﬁers.

• Stacked Generalisation: This method was intro-

duced by Wolpert(Wolpert, 1992), using a set of

classiﬁers denoted by C

, C

, ..., C

which

are trained ﬁrst, so that an individual classiﬁcation

for each of them is obtained, which are called the

First Level Base Classiﬁers. After obtaining these

individual classiﬁcations, a majority voting crite-

rion is selected, thus constructing the ﬁnal classi-

ﬁer, this phase is called Second Level Meta Clas-

siﬁer.

• Mixture of Experts: This method is similar to

Stacked Generalisation, it considers a set of clas-

siﬁers denoted by C

, C

, ..., C

, to per-

form ﬁrst level base classiﬁers, later a classiﬁer

T +1

combines the individual classiﬁcations of

each one considered, ﬁnding the ﬁnal classiﬁca-

tion. This model considers a phase in which the

weights are assigned to each classiﬁer C

, i =

1,2,...,T , to ﬁnally apply a criterion of weighted

majority voting. Usually this part of the model is

performed by a neural network, called the gating

network(Polikar, 2006).

These are some approaches of how classiﬁcation

can be performed in Data Mining using ensemble

based algorithms, they have been shown to be very

successful in improving the accuracy of classiﬁers for

artiﬁcial and real world DB, in this work we focused

on stacked generalisation using a weighted majority

voting criterion to combine class labels, in the next

Section our proposed algorithm is given in detail.

3 HYBRID CLASSIFIER WITH

GENETIC WEIGHTED (HCGW)

To construct any type of ensemble based systems,

three points are due to consider:

1. The ﬁst point is to establish the number of clas-

siﬁers that we will use, as well as the type of each

of them. This is seldomly done generally using

only one classiﬁer such as decision trees.

2. The second point is the structure of the ensemble,

by means of which we will be able to group each

one of the classiﬁers, in the last section we saw

four different approaches for this.

3. Finally a criterion for combining the indivi-

dual classiﬁcations is chosen, majority voting or

weighted majority voting.

In this section we will describe how to construct

the HCGW, taking as reference the three points men-

tioned earlier. This is discussed in the following sub-

sections.

3.1 Number and Type of Classiﬁers

For this element of the HCGW we had to decide the

type, quantity and selection criterion of the different

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

360

classiﬁers. In the literature we have a large number of

these, however we can not test every one of them, so

we took as an starting point the paper entitled ’Top 10

algorithms in data mining’ of J. Ross Quinlan (Quin-

lan et al., 2008), which presents the top ten algorithms

of classiﬁcation.

Once we decided on which could be possible can-

didates, we had to use a selection criteria based on the

problematic we have, these criteria are listed below:

1. The implementation of a classiﬁer should be sim-

ple.

2. Low running time.

3. Since it is an ensemble based system it is not

required to have a high percentage of accuracy,

since our objective is to gather various types of

classiﬁers to improve accuracy.

4. Finally, the classiﬁers selected, must support large

amounts of data.

After experimenting with classiﬁers from Quin-

lan’s paper and some others, we found that some clas-

siﬁers do not meet the criteria that we set earlier, for

instance Support Vector Machine meet criteria one

and three, but two and four not fulﬁlled as it does not

support large amounts of data and the running time

is very high. We ﬁnally selected six classiﬁers that

meet the criteria. We have ﬁve supervised learning

(Naive Bayes, k-NN, Decision Tables, ADTree, C4.5)

and one unsupervised learning (K-Means) algorithms.

3.2 Structure of Ensemble

Having these six classiﬁers, we must establish the

structure for our ensemble based algorithm, we chose

mixture of experts, putting in one stack all the classi-

ﬁers. The selection of Mixture of Experts was due to

the fact that this type of ensemble based systems gives

us the chance to take the opportunity to use many dif-

ferent classiﬁers, which in Baggin and Boosting is not

used. This combined with a weighted voting approach

is a novel approach and the results showed that it is

good one.

3.3 Criterion of Combination of the

Individual Classiﬁcations

Each classiﬁer considered, has different degrees of

accuracy, one of the characteristics of the models of

mixture of experts ensemble, and therefore we must

determine which criterion for combining the individ-

ual classiﬁcations to use, for constructing the classi-

ﬁer C

T +1

As seen in the previous section for the mixture of

experts it is common to use neural networks, however,

neural networks have some issues, as the problem of

generalisation, in which the neural network learns the

training data correctly, but is not able to deal with to

new data. Another problem arises when using gra-

dient descent method to minimize the error, which

runs the risk of being trapped on local minimal and

not ﬁnding the best way to assign weights of classi-

ﬁers. To ﬁnd the best form to weigh each classiﬁer,

considering these problems, we use a different way

to assign them, which is genetic algorithm. To solve

the problem of being trapped in local minimum and

maximum, genetic algorithms have the genetic opera-

tor called mutation, which reduces the probability that

this occurs.

Since different weights give a different accuracy,

how can we know what is the best conﬁguration? the

answer that we use was applying a simple genetic al-

gorithm, in which each population represents weights

for each of the classiﬁers. We chose six different

classiﬁers, thus the size of each chromosome in our

genetic algorithm was six. The codiﬁcation of each

chromosome, has a speciﬁc weight in the range of [0,

0.5, 1, 1.5, 2, . . . , 4], deﬁned arbitrarily.

In order to ﬁnd the best combination of weights

assigned to each classiﬁer, we must set the size of

the training and test set, for obtaining the individual

accuracy of each classiﬁers. Since we used a large

DB with a total of 379,485 records, a 10% random

sample is selected of the DB in order to avoid a long

runtime. This was selected since it was a good trade-

off between accuracy and runtime. It also falls in line

with statistical sampling. To do a simple random sam-

pling, as in our case, we have the following analysis

to obtain the sample size. Considering a conﬁdence

level of 0.95, with a maximum error of 0.1 and a pi-

lot study gives a variance of 154.5, according to the

sample random simple calculation we have:

′

α/2

· σ

where:

• n

′

possible sample size,

• z

α/2

is the conﬁdence level chosen,

• σ

population variance,

• e: maximum error,

If it is true that N > n

′

−1), where N is the total

size of the data, it takes the value of n

′

as the sample

size, otherwise it will calculate a new sample size n,

as shown below:

A HYBRID CLASSIFIER WITH GENETIC WEIGHTING

361

n =

′

1 +

′

In this particular instance once we have the per-

formed the calculations we obtain a sample size of

51325. The value of the sample obtained represents

13.5% of the DB, we used 10% for practical reasons

and think is appropriate because it is near the value

obtained by statistical analysis.

Once the phase of training for each classiﬁer is

ﬁnished, we obtain the individuals classiﬁcations, ha-

ving these we generate a population for the genetic

algorithm, where each chromosome represents a di-

fferent combination of weights. The genetic algo-

rithm is then executed a ﬁxed number of iterations

using as the objective function to maximise accuracy,

using the weighted majority voting criterion to com-

bine class labels. The best combination of weights

found for this DB is in Table 1.

Table 1: Weights assigned to classiﬁers.

Case Name Weighted

1 Naive Bayes 3

2 ADTree 2.5

3 Decision Tables 1.5

4 C4.5 2

5 k-Nearest Neighbours 2

6 K-Means 2.5

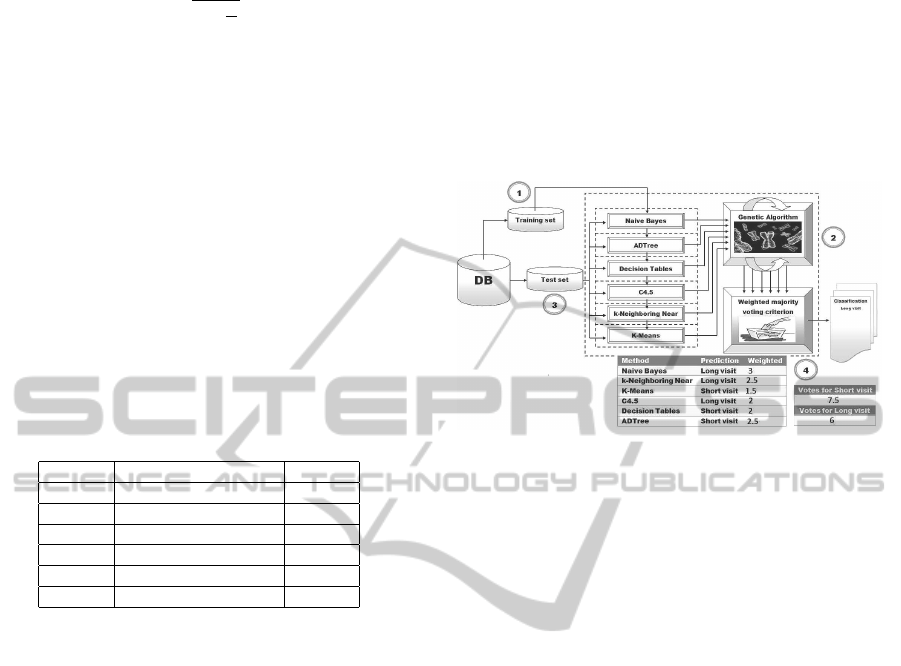
3.4 Operation of HCGW

The operation of HCGW consists of the following

stages:

1. Training of the HCGW: First a random subset

of the DB is generated, to be able to begin with

the phase of training of each classiﬁer considered.

Each of the classiﬁers is trained by a different

training set, selected randomly from the data base.

We use different training sets because they are tai-

lored for each classiﬁer which is executed.

2. Conﬁguration of Weights: A 10% test set is se-

lected (this percentage was used for the DB of

ECML PKDD, however this percentage can be

adjusted depending on the DB using). Once the

classiﬁcation data is obtained, it is given to the ge-

netic algorithm which is executed for a ﬁxed num-

ber of generations. This procedure is performed

only once.

3. Individual Classiﬁcations: The individual clas-

siﬁcations for each classiﬁer are obtained, consi-

dering the test set.

4. Combination of the Individual Classiﬁcations:

A weighted majority voting criterion is used to

combine class labels, so that for each of the exam-

ples in the test set we get its classiﬁcation. In Fi-

gure 1 we can observe the scheme of operation of

the HCGW with an example of how such classiﬁ-

cation is performed.

Using our test DB we performed some experi-

ments with HCGW which are discussed in the Section

of Tests and Results.

Figure 1: Operation of the HCGW.

4 DB AND LEARNING TASK

As was mentioned before we use a DB which is from

ECML PKDD, this data was provided by the Gemius

Company, which is dedicated to the monitoring of In-

ternet on central and Eastern Europe. Within the DB

there were different problems to solve, but for this

work we only focus on one of them, which consists

in the following:

• The Length of the Visit. A visit is a sequence of

Page Views by one user. As web pages are identi-

ﬁed by their categories, during one visit user may

view pages of one or more categories. Therefore

we deﬁne:

– Short visit: is a visit with page views of only

one category.

– Long visit: is a visit with pages views of two or

more categories.

The learning task is to answer the question

whether a given visit is short or long. The following

section will be dedicated to describe the experiments.

5 EXPERIMENTS

In this section we will review different experiments

performed on the DB. First, we will discuss the se-

lection of the test and training sets, the percentage

of the DB that we used to ﬁnd the weights of the

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

362

HCGW and the performance measures to consider.

Regarding the division of the data, in each experi-

ment we selected thirteen subgroups of random ele-

ments of the DB, where the distribution of the whole

DB was conserved, roughly 75% are short visits and

25% are long, having a size of 5,000, 10,000, 20,000,

40,000, 80,000, and so on in multiples of 40,000 until

360,000, the last set is the full DB (379,485 records)

These thirteen subgroups conformed our test and

training set, that is to say, for the training set, the class

of each one of the examples is conserved, which is the

type of visit. For the test set, we eliminated the class

of each example, conserving the other attributes.

In the experiments carried out with the DB of

EMCL PKDD, there are only on two classes due to

the structure of the DB, but since implementations of

each component are our own, data can be classiﬁed

with more than two classes.

Once we had these sets, we selected the data for

the genetic algorithm, in order to ﬁnd the weights of

each one of the classiﬁers. We must take into account

the great number of iterations due to the size of the

population, for example, if we have 10,000 examples

that were classiﬁed of individual way by the six clas-

siﬁers, we will have a matrix 6 X 10,000. For this

matrix we must test each chromosome, to see what

which is the ﬁnal classiﬁcation with that combination,

and thus repeat until obtaining the function of aptitude

of each chromosome.

Within machine learning there are different per-

formance measures, in this paper we only show the

results of Accuracy. Accuracy is the percentage of

examples classiﬁed correctly in the test set.

In the following section we will present the re-

sults found when performing these experiments with

the thirteen sets, comparing different tools against the

HCGW, showing the accuracy results obtained.

6 RESULTS

The following tools for Data Mining(Witten and

Frank, 2005): SIPINA(Witten and Frank, 2005),

TANAGRA(Witten and Frank, 2005), WEKA (Wit-

ten and Frank, 2005) and our own implementations in

Matlab R2008b (7.7), were employed, and they were

used in the classiﬁcation of the Gemius DB.

We selected different sizes of training set and the

thirteen subgroups, to be able to perform classiﬁca-

tion with the four previous tools. Were tested with

a set of classiﬁers for each tool consideration, how-

ever for this paper those which showed the best results

are Ensemble Based Systems so we focused on them.

First we will show the results for ensemble based sys-

tems of tool WEKA and then we will select the best

tools to compare against HCGW.

For ensemble based systems we selected the tool

WEKA, since it has a large number of algorithms

implementing this type of classiﬁer, and its imple-

mentations gave the best accuracy, the results with

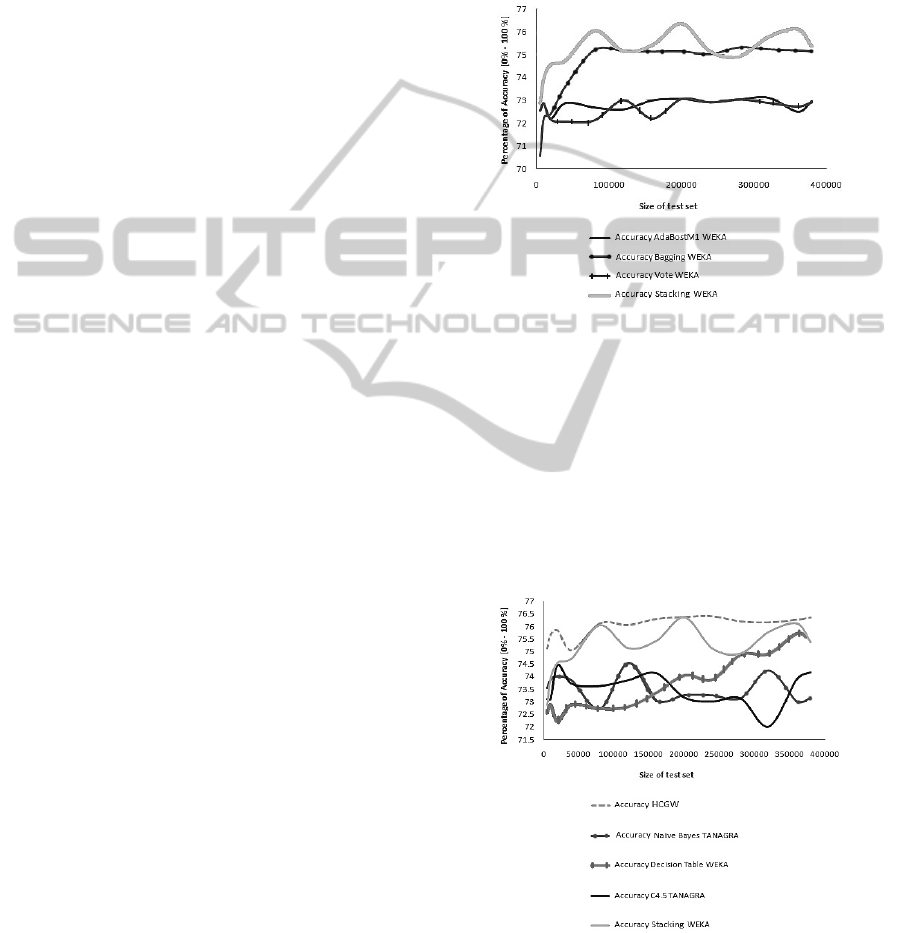
Ensemble Methods are shown in Figure 2.

Figure 2: Comparison of accuracy of Ensemble Methods.

In Figure 2 the Stacking method shows the most ac-

curacy, this method is similar to our HCGW, it is a en-

semble methods of type Stacked Generalisation (vot-

ing by majority), but it only considers decision trees

to classify, and not several different methods as we

do. The tool achieves a 75.19% in accuracy. Finally

we calculated the accuracy for our HCGW, and com-

pared the results for each one of the thirteen sets, with

the best results previously obtained, Figure 3 shows

these results.

Figure 3: Comparison of accuracy with HCGW.

As we can see in Figure 3 the accuracy grew

2.26% with respect to the other methods considered

for the tests, this gives us the result that the HCGW

performs better than traditional techniques.

A HYBRID CLASSIFIER WITH GENETIC WEIGHTING

363

Once these results with this DB were obtained, we

did a t-Test, taking accuracy from the HCGW and

the one from Stacking of WEKA, obtaining a level

of signiﬁcance high since we are conﬁdent with a

99.9995% that the results of our model are signiﬁ-

cantly different and better than those than we obtained

with Stacking of WEKA.

Figure 4: Comparison of times.

In Figure 4 we can see the runtimes of the tools

we used, we can observe that Stacking of WEKA and

HCGW are those that take more time. This is ex-

pected as they use several classiﬁers, the complexity

of our algorithm is approximately equal to the sum

of the individual complexities of the classiﬁers used.

The results obtained with this DB and some results

with the UC Irvine repository(Frank and Asuncion,

2010), are shown in Table 2:

Table 2: Final comparison of results.

Name Records HCGW Stacking (WEKA)

Gemius complete 379485 76.03 75.19

Credit (German) 1000 72.33 71.75

Mushroom 8124 92.46 95.63

Australian 690 84.12 82.75

In the Table 2 we can observe that for DB

Gemius complete, Credit and Australian, the accu-

racy of the HCGW is better than the methods of tool

WEKA, which were chosen because they have bet-

ter accuracy than other tools. For Mushroom, Stack-

ing obtains a better accuracy which can be explained

since is best ﬁtted to a decision tree method as done

by WEKA classiﬁer has better results than us and this

was adjusted in a better way to this DB has a small

size, the No free lunch(Wolpert and Macready, 1997)

theorem applies here, since there is no classiﬁer that

is the best for all the problems.

7 CONCLUSIONS AND FUTURE

WORK

This paper presents an ensemble based algorithm of

type stacked generalisation, taking several types of

classiﬁers and implements a weighted majority vot-

ing criterion to combine class labels, using a genetic

algorithm to assign the weights each classiﬁer. This

model of classiﬁcation we called it a Hybrid Classi-

ﬁer with Genetic Weighting, which is a novel algo-

rithm, because it actually considers several type of

classiﬁers, and not only decision trees like normally

found in the literature. It uses as well a genetic algo-

rithm for the allocation of weights. With this model of

classiﬁcation, we obtained a better accuracy for each

one of the tests we made to the DB gemius complete,

comparing it with different methods from other tools.

Since running time is a major issue as future work we

will look into parallel computing as means to solve it.

There would be parallel versions of each classiﬁer, the

genetic algorithm as well as the HCGW component

that handles the combination of individual classiﬁca-

tions. This, we believe, would lower the total running

time allowing larger data sets to be handled as well as

being able to consider some other classiﬁcation algo-

rithms which were too costly for this work.

REFERENCES

Bauer, E. and Kohavi, R. (1999). An Empirical Comparison

of Voting Classiﬁcation Algorithms: Bagging, Boost-

ing, and Variants., volume 36. Kluwer Academic Pub-

lishers.

Breiman, L. (1996). Bagging Predictors., vol. 25. Kluwer

Academic Publisher.

Frank, A. and Asuncion, A. (2010). UCI machine learning

repository.

Kelly, J. D., J. and Davis, L. (1991). A hybrid genetic

algorithm for classiﬁcation. In Proceedings of the

Twelfth International Joint Conﬁrence on Artiﬁcial In-

telligence., pages 645–650.

Polikar, R. (2006). Ensemble based systems in decision ma-

king. IEEE Circuits and Systems Magazine 6:21-45

Quinlan, J. et al. (2008). Top 10 algorithms in data mining.

Knowledge and Information Systems., 14:1–37.

Schapire, R. (2001). The boosting approach to machine

learning: An overview. AT&T Labs Research Shan-

non Laboratory.

Witten, I. and Frank, E. (2005). Data Mining: Practi-

cal Machine Learning Tools and Techniques. Morgan

Kaufmann Publishers. 2nd edition.

Wolpert, D. (1992). Stacked generalization. Neural Net-

works., 5:241–259.

Wolpert, D. and Macready, W. (1997). No free lunch the-

orems for optimization. Evolutionary Computation,

IEEE Transactions on, 1:67–82.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

364