PLICAS
A Texas Hold’em Poker Bot
Christian Friedrich
Business Information Systems and Operations Research, Technical University Kaiserslautern
Erwin-Schr¨odinger-Str. Geb. 42, D-67663 Kaiserslautern, Germany
Michael Schwind
Institute for Information Systems, Gr¨uneburgplatz 1, 60323 Frankfurt Main, Germany
Keywords:
Multiagent-system, Intelligent agents, Case-based reasoning, Game theory applications.
Abstract:
Since two decades, poker is a very popular game and in the last decade poker became also an interesting topic
in game theory (GT), artificial intelligence (AI) and multi-agent systems (MAS). This paper describes the
development and evaluation of the poker bot PLICAS designed for the variant ‘Texas Hold’em Fixed Limit
Heads-up’. In the development process, approaches such as opponent modeling, abstraction techniques, and
case-based reasoning were studied and implemented. PLICAS also introduces simulation-based methods for
the exploitation of the opponent’s play. In the experimental part of this paper, we analyze the strengths and
weaknesses of PLICAS, which participated in the 2010 AAAI Computer Poker Competition (ACPC).
1 INTRODUCTION
Poker is a game with imperfect information in con-
trast to games with perfect information such as chess
(Hamilton and Garber, 1997) or checkers (Schaeffer,
1997). For perfect information games there are so-
lution approaches that can compete with the world’s
best human players, while games with imperfect in-
formation did not enter the research focus until the
end of the nineties (Koller and Pfeffer, 1997). In the
recent years many poker bots have been developed for
the ‘Texas Hold’em Fixed Limit’ variant
1
. This has
resulted in a significant improvement in the quality
of playing poker bots driven by the AAAI Computer
Poker Competition (ACPC)
2
. Recent bots use ab-
straction methods to handle the complexity of poker
(Davidson et al., 2000) or employ classical AI ap-
proaches for opponent modeling and decision making
(Billings et al., 2003). While these approaches mostly
specialize on a single particular aspect or phase of the
poker game and the implementation of suitable solu-
tion methods derived from GT, AI, and MAS, such
as learning and reasoning techniques, we follow a ho-
1
Poker rules & variants: www.pagat.com/poker/rules/.
2
www.computerpokercompetition.org
listic hybrid approach. For that reason, this paper
presents the concept, architecture, and evaluation of
the poker bot PLICAS
3
, which uses a combination
of case and rule-based reasoning together with sim-
ulation, abstraction, learning, and opponent modeling
techniques to create a decision making process for the
relevant phases of the poker game. Additionally, PLI-
CAS uses preflop ranges for determining the optimal
bluffing frequency, which is a new approach. After an
overview of the literature on automated poker play,
we present the architecture, methods, and algorithms
of PLICAS followed by the presentation of some ex-
periments in order to initially evaluate the bot and the
results of 2010 ACPC which PLICAS participated in.
2 A SHORT OVERVIEW OF
AUTOMATED POKER PLAY
The seminal scientific work on poker is mainly based
on GT. The pioneers of GT, such as (Neumann and
Morgenstern, 1944), (Kuhn, 1950) and (Nash and
Shapley, 1950) present some game theoretic analysis
3
The word ‘fold’ (lat. plicare) describes the action of
laying down cards and quitting the game.
63
Friedrich C. and Schwind M..
PLICAS - A Texas Hold’em Poker Bot.
DOI: 10.5220/0003465300630072
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 63-72
ISBN: 978-989-8425-54-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

for simplified versions of poker in their early work.
Due to the complexity of poker it was merely im-
possible to think about using their work for building
automated poker players until the last decade. (Koller
and Pfeffer, 1997) are the first to analyze poker and
imperfect information games from a game theoretical
point of view with respect to automated play. They
present the design for the theory-based GALA system
which is able to deal with the imperfect information
problem in poker. However, this system remains
purely theoretical and has not been implemented yet.
(Billings et al., 1998) published the first article
about a poker bot implementation called LOKI. This
bot introduces opponent modeling which allows an
adaptive playing style trying to exploit the weak-
nesses of the opponent. The decision making process
of LOKI is mainly rule-based. A revised version
of LOKI is the poker bot POKI which uses neural
net-based opponent modeling (Davidson, 1999),
efficient hand strength simulation and probability
triples for probabilistic decision making (Billings
et al., 1999; Davidson et al., 2000).
Opponent modeling is often coupled with bluffing
which is essential in real-world poker. (Southey
et al., 2005) present a opponent modeling poker
bot which uses bluffing strategies. (Neumann and
Morgenstern, 1944, p. 189) characterize bluffing as
follows: ‘Of the two motives for bluffing, the first
is the desire to give a (false) impression of strength
in (real) weakness; the second is the desire to give a
(false) impression of weakness in (real) strength.
Another technique used to enhance poker play in
connection with opponent modeling is abstraction.
The poker bot PsOpti uses an abstraction technique
named bucketing where hands are classified into
‘buckets’ in accordance with their strength. Addition-
ally a betting round reduction is realized by merging
pre- and postflop behavior. These techniques are
combined with a pseudo-optimal playing strategy
which tries to approximate a Nash equilibrium for
poker games (Billings et al., 2003).
Approximating the Nash equilibrium (ε-
equilibrium) strategy is a very common technique in
automated poker play. A Nash equilibrium strategy is
designed to avoid losing for the poker bot in contrast
to the opponent modeling strategy which aims at
winning a game by exploiting weaknesses. This is
because no matter what playing strategy the opponent
adopts, the ε-equilibrium strategy ensures that the
opponent can not win more than the equilibrium
solution allows for. The approximation is needed
because extreme large size of the poker game tree
(Billings et al., 2003).
After having substantial success with PsOpti
while playing against human poker players of even
world-class level, (Billings et al., 2003) present
a further bot called BRPlayer. This bot employs
heuristic search and uses the ‘expectimax’ algorithm
to exploit the opponents’ strategies (Schauenberg,
2006). The ‘expectimax’ strategy is a subtype of the
min-max strategy. In a min-max strategy each player
tries to minimize the maximum payoff possible for
the opponent. If the game is a zero-sum game,
this strategy also maximizes minimum payoff of
the player. Expectimax is a min-max strategy that
works with expected values due to the stochasticity
of poker. Another type of min-max strategy is the
min-regret approach that minimizes the worst-case
regret. Regret is defined as the difference between
the actual payoff and the payoff that could have been
obtained if the player would have chosen another
action. Min-max strategies are usually employed to
find the ε-equilibrium strategy in a Nash game.
Latest poker bots with successful playing strate-
gies use case-based reasoning to make playing
decisions. In (Watson and Rubin, 2008), published
CASPER, a bot which introduces case-based rea-
soning in multi-player poker. A heads-up version of
CASPER, called SARTRE, was fairly successful in
the 2010 ACPC (Rubin and Watson, 2009; Rubin and
Watson, 2010).
3 ESSENTIAL TECHNIQUES FOR
AUTOMATED POKER PLAY
Summarizing the models for playing automated poker
that have been presented in the previous section, we
give a short overview of standard techniques, that are
currently used to design poker bots:
• Case-based Reasoning is used to find suitable ac-
tion in the playing process. Without bucketing
large databases are needed to cover all situations.
• ε-equilibrium is an approximation to the Nash
equilibrium strategy. The strategy is designed to
avoid losing the game. ε-equilibrium strategy is
often used together with min-max optimization.
• Min-max Strategy minimize the maximum pay-
off possible for the opponent. The min-regret and
the expectimax strategy are variants of the min-
max approach.
• Opponent Modeling is an adaptive playing style
that tries to exploit the weaknesses of the oppo-
nent. In contrast to the ε-equilibrium strategy,
opponent modeling is designed to win the game
while increasing the risk of losing it.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
64

Table 1: Ranking of starting hands into buckets (numbers denote classes).
suited
A K Q J T 9 8 7 6 5 4 3 2
off suite
A 1 1 2 2 3 4 4 5 5 5 5 5 5
K 2 1 2 3 3 5 6 6 6 6 6 6 6
Q 3 4 1 3 4 5 6
J 4 5 5 1 4 5 6 7
T 4 5 5 5 2 5 6
9 7 7 6 6 3 6 6 7
8 7 7 7 6 4 6 7 7
7 7 5 7 6 7
6 7 6 7 6
5 7 6 7 7
4 7 6 6 7
3 6 7
2 6
• Learning refers to all memory-based techniques
which are designed to exploit former experience
for finding better future playing strategies.
• Bluffing has the goal to cause at least one oppo-
nent who holds a better hand to quit the game.
• Simulation produces pre-play results which are
stored in a memory and can be exploited for better
strategy selection in the course of a poker game.
• Bucketing is an abstraction technique that re-
duces the complexity of the game. Several deci-
sion situations in the game are treated in the same
way. They are put into the same bucket.
Because bucketing is an essential technique for
PLICAS, we will give an example how it works to-
gether with the ranking of starting hands. Table 1
shows an example using eight equivalence classes.
The term ‘suited’ and ‘off suit’ means that a hand has
the same color (e.g. 8♦,9♦) respectively different
colors (e.g. 8♥,9♠). Class one includes the strongest
starting hands: A♦A♠,K♦K♠, Q♦Q♠, J♦J♠ and
A♦K♦. These hands can bet handled with the same
strategies in the first round. The higher the number
in Table 1 is, the weaker is the starting hand class. A
hand such as J♥, 8♠ is considered as just playable.
Hands marked in gray are falling into class eight and
are considered as not playable.
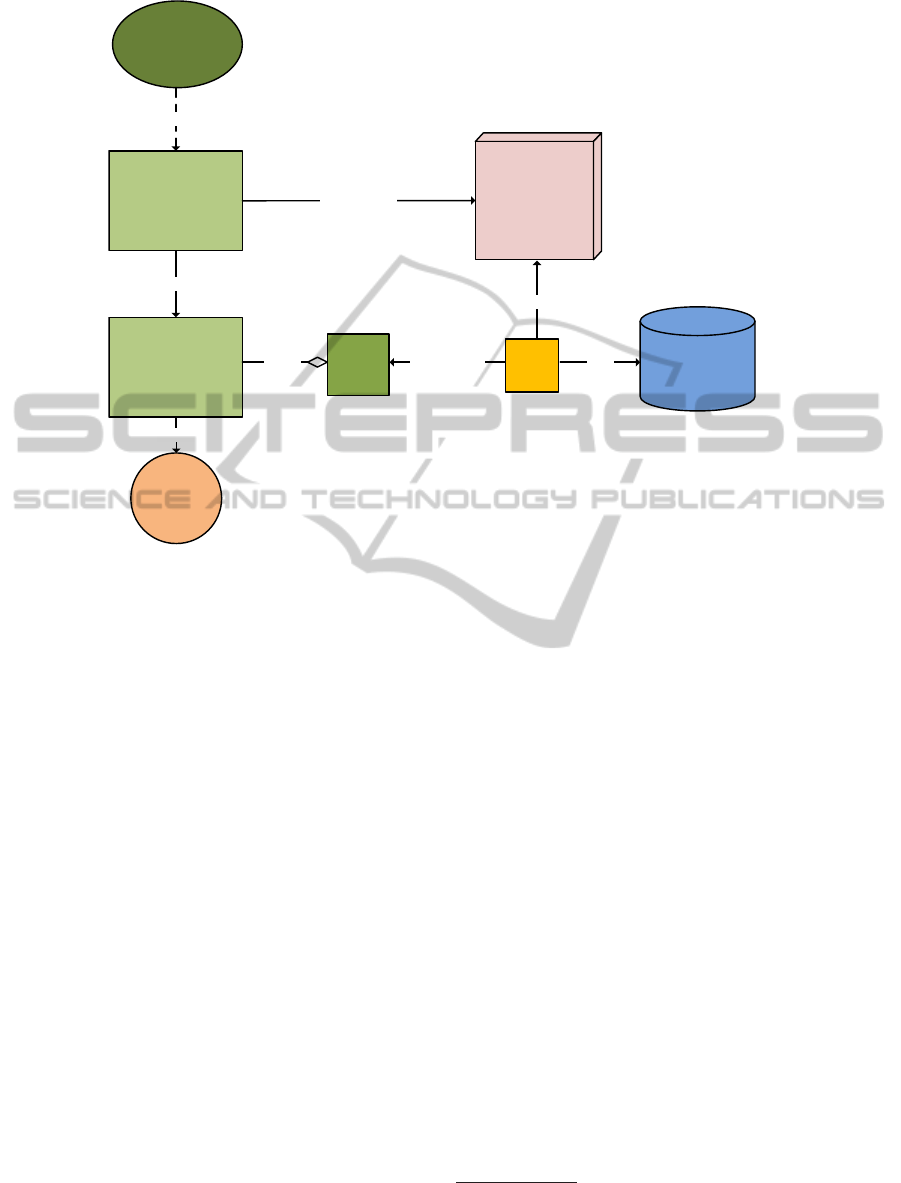
4 SYSTEM ARCHITECTURE
AND PLAYING ALGORITHMS
The general system architecture of PLICAS is de-
picted in Fig. 1. Several decision units have influence
on the global decision process that can end in a ‘fold’,
‘call’, or ‘raise’ action during the game. A rule-based
based unit contains the logic for these decisions. PLI-
CAS uses basically rules that are generically derived
Opponent
Model
Rule-
based
Decision
Unit
Decision
Unit 2
Table
Perceive
Situation
Decision
Unit 3
Decision
Decide
Decision Process
Additional Units
Figure 1: System architecture of the PLICAS poker bot.
from classical expert rules for poker play, like those
published by (Sklansky, 1997). These decisions also
depend on the data collected by the opponent model
unit in the course of the game. Poker play in gen-
eral has four phases: the flop, the turn, the river
and the showdown. These can be grouped into two
main phases: the preflop phase before the flop cards
are dealt and the postflop phase afterwards (including
turn, river, and showdown). For this reason the PLI-
CAS bot uses two decision units, one for the preflop
phase and another for the postflop phase (including
turn, river, and showdown). The dichotomy of the de-
cision units producesinterdependencies: observations
made in the preflop phase (opponent’s played hand
ranges
4
) influence decisions in the postflop phase and
vice versa (opponents postflop aggression influences
preflop play).
4
A hand range is a subset of all possible starting hands.
PLICAS - A Texas Hold'em Poker Bot
65







 


 

!





"

#$$ %
&

'
(
(
)*

(+
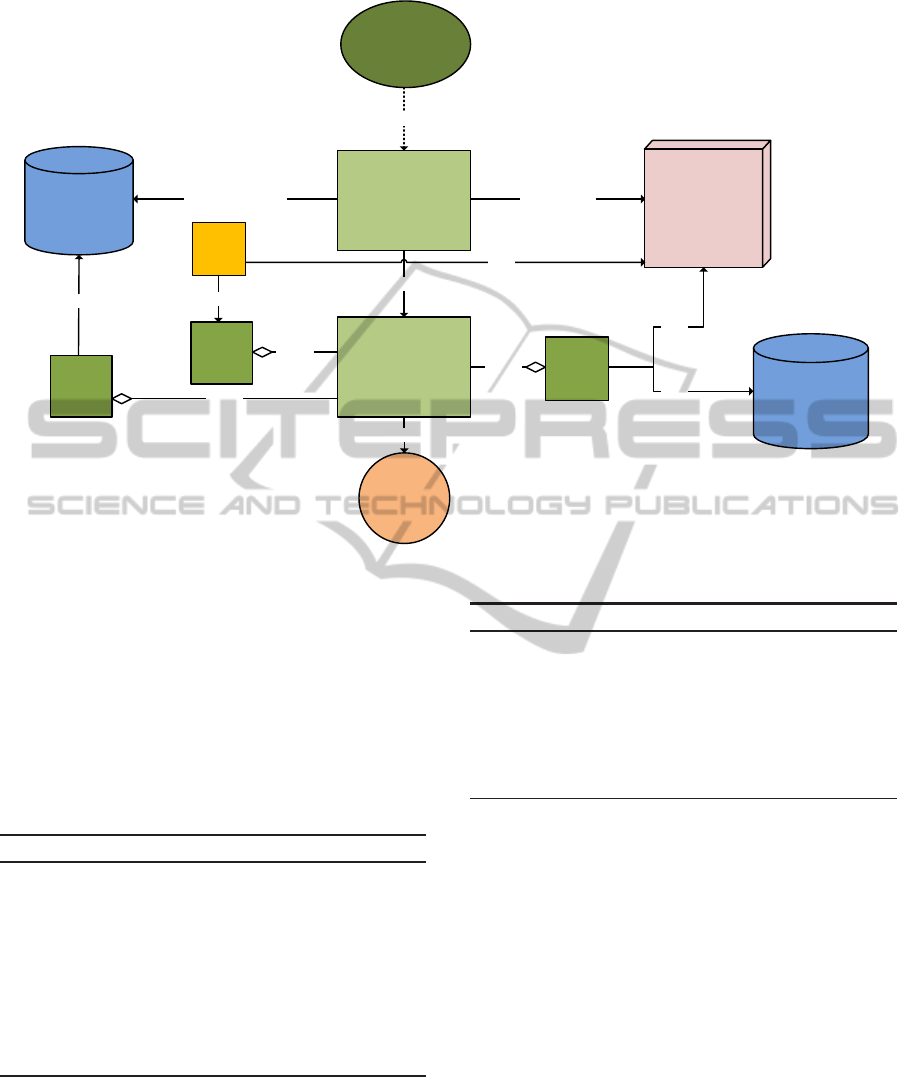
Figure 2: System architecture of the PLICAS preflop decision model.
4.1 The Preflop Model
PLICAS’ decision model for the preflop phase is de-
picted in Fig. 2. Information gathered in the preflop
phase is very important for getting an idea of how the
opponent plays. For this purpose, PLICAS has been
given an opponent model, which registers how often
the opponent raises and calls before the flop. The op-
ponent’s aggression, the proportion of raises and calls
during the game, is also measured. The information
about the percentage of hands (range) the opponent
does not fold before the flop is the most essential for
adapting play. The output of the preflop phase de-
cision process is a probability triple pt(r,c, f). This
triple helps PLICAS to decide when to fold, call, or
raise during the game. PLICAS’ preflop system is
endowed with the simulation-based dynamic preflop
range control (DPRC) and a rule-based decision unit.
4.1.1 Rule-based Decision Unit (Preflop)
This unit provides the basic rules for decision making
process of PLICAS. The preflop decisions are ratio-
nal decisions based on the opponent’s actions and an
hand ranking according to expected values (EV). The
EV is the probability that a starting hand will win the
game (pot) against another starting hand at the show-
down, without knowing any postflop cards. Decisions
whether to call, fold or raise are made on base of
expert-knowledge for Texas Hold’em Poker, which is
represented as a set of rules.
PLICAS classifies 169 starting hands according
to their approximated EV against a large number of
other starting hands. The calculation of the EV is
done by using the ‘Pokerstove’
5
tool and the result
is comparable to the starting hand ranking presented
in Table 1. There are other popular hand ranking ap-
proaches like the (Sklansky, 1997) hand ranking for
multi-player matches which does not use the EV as a
main attribute. We decided to use an EV-based hand
ranking mechanism because the EV is important in
heads-up matches. Due to the fact that there are only
two players involved in heads-up matches, the EV can
be easily used to assess whether run a bet, call, or raise
has a positive or negative return in the long.
4.1.2 Dynamic Preflop Range Control
The DPRC unit automatically adapts the opponent’s
preflop hand ranges by balancing the cost of preflop
folding and the increase in the EV at the flop deriving
from a tighter preflop range.
6
The following func-
tion is used for the calculation of the adapted preflop
5
www.pokerstove.com
6
Range is called tight if the number of starting hands is
small and loose if it is high.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
66

range:
f(r
p
,r
o
, p
avg
) = EV(r
p
,r
o
)(p
avg
/2)
+(1− EV(r
p
,r
o
))(−p
avg
/2)
+(r
o
− r
p
)(−1)
r
p
: one’s own preflop range
r
o
: the opponents’ preflop range
p
avg
: the average pot size
In this formula EV(r
p
,r
o
) gives the percentage of
how often range r
p
defeats range r
o
at the showdown
without knowing any postflop cards. For example a
range of 0.1 (10%) has an EV of 55% against a range
of 0.15 (15%). A range of 0.1 represents the set
of hands: {88+,A9s+,KTs+,QTs+,AJo+,KQo},
whereas the range 0.15 represents the set of hands:
{77+, A7s+, K9s+, QTs+,JTs,ATo+,KTo+, QJo}
7
The rest of the formula can be explained as follows:
The first addend EV(r
p
,r
o
)(p
avg
/2) represents the
chance of winning the pot postflop multiplied by
the possible winnings, which is half the pot size.
By contrast, the second addend (1 − EV(r
p
,r
o
))
(−p
avg
/2) is the chance of loosing the pot postflop
multiplied by the possible loss, which is also half
the pot size. The third addend (r
o
− r
p
)(−1) is
the amount PLICAS looses by folding more often
than the opponent in the preflop betting round. For
example, PLICAS’ range r
p
is 0.5 and the opponents
range r
o
is broader with 0.6. So PLICAS folds in
10% (r
o
− r
p
= 0.1) of the cases when the opponent
would not. In these cases he looses 1 SB
8
, which is
an average loss of −0.1 · SB per hand. The function
represents a trade-off between gaining - by having
an EV-advantage postflop based on a tighter preflop
range - and loosing - by having a higher folding rate
in the preflop phase. For performance reasons, the
simulation for determining the EV is not performed
at runtime. A lookup table holds the precalculated
simulation results for 169 preflop ranges playing
against each other in a 169× 169 matrix. The starting
hands categories are abstracted to 169 following
the position equivalency isomorphism and the suit
equivalency isomorphism described by (Billings
et al., 2003). Algorithm 1 describes the DPRC
7
The nomenclature is as follows: ’s’ means that the
cards’ suits are the same, ’o’ means that the suits are dif-
ferent. ’+’ means that hands that dominate the stated hand
are also included in the range. A pocket pair is dominated
by other pocket pairs with a higher rank. A non-pair hand is
dominated by a hand with the same high-card and a higher
kicker.
8
A ‘small blind’ (SB) is the smallest money unit that can
be bet with, a ‘big blind’ (BB) has the double value of a SB.
process. A relation is defined on the set of ranges. It
specifies the dominance relationship of two ranges
r
p
and r
o
based on the function f(r
p
,r
o
, p
avg
) intro-
duced above. If a specified number of hands n ∈ N
was processed by the opponent model, the DPRC
maximizes f(r
p
,r
o
, p
avg
) using fixed values for r
o
and p
avg
. The adapted level of one’s own hand range
r
p
is the local maximum of f(r
p
,r
o
, p
avg
).
Algorithm 1: Dynamic Preflop Range Control.
∀r
o
∈ [0,1] : ∃r
p
∈ [0, 1] : r
p
≥ r
o
r
p
≥ r
o
⇔ r
p
dominates r
o
⇔ f(r
p
,r
o
, p
avg
) ≥ 0
if OpponentModel.numHands > n then
r
o
= OpponentModel.range
p
avg
= OpponentModel.avgPot
r
p
∈ [0,1] with r
p
≥ r
o
f(r
p
,r
o
, p
avg
) → max!
end if
4.2 The Postflop Model
The function the postflop decision model is shown in
Fig. 3. After the three flop cards are dealt the size of
the decision tree of the game increases significantly
and decision making becomes more difficult. PLICAS
uses the abstraction technique bucketing to keep the
complexity at a level which can still be handled. The
postflop decision process also involves a rule-based
decision unit. Additionally, a case-based decision
unit, a simulation-based unit for bluffing, and a unit
for adapting the opponents aggression affect the post-
flop decision process. These units enable PLICAS to
pursue a flexible return maximizing strategy (Billings
et al., 2003) by exploiting the opponents style of play.
As for preflop, the postflop decision model generates
a value triple pt(r,c, f) that contains the probabilities
for PLICAS’s actions fold, call, or raise.
4.2.1 Rule-based Decision Unit (Postflop)
The rule-base contains rules that form a basic playing
strategy. On the one hand, these rules enable the bot
to avoid unprofitable play in order to minimize losses,
on the other hand, the rules produce static playing be-
havior which is not capable of exploiting the oppo-
nents weaknesses to maximize PLICAS’s profit. To
do this, Algorithm 2 periodically perceives the situa-
tion s during the game and checks, whether the situ-
ation is suitable for bluffing. This is the case, if the
opponent did not yet actively invest in the ‘pot’ (is-
FirstAction) and the own hand is classified as ‘isNot-
PlayableHand’. If the situation allows bluffing, PLI-
CAS performs a bluff with a probability that depends
PLICAS - A Texas Hold'em Poker Bot
67







 




















!

"##$
%
&

'
'
()
'

'*'

Figure 3: Postflop decision model of the PLICAS poker bot.
on the opponent’s preflop range (see Section 4.2.3).
In the ‘not bluffing’ case, the rule base computes the
appropriate probability triple pt(r,c, f) for the situa-
tion s according to a set of rules based on (Sklansky,
1997). Additionally, if the case-based decision unit
(see Section 4.2.2) contains more than n previously
recorded playing cases (threshold of operation) a sec-
ond probability triple is generated. Both probability
triples are then merged and used for decision making.
Algorithm 2: Postflop Decision Process.
Perceive situation s
if isFirstAction ∧ isNotPlayableHand then
bluff(opponentModel.range)
else pt(r,c, f) = ruleBase.getTriple(s)
end if
if |CaseBase| > n then
pt = merge(pt(r,c, f),CaseBase.getTriple(s))
decide(pt(r, c,f))
end if
4.2.2 Case-based Decision Unit
Hands going to the showdown are evaluated and
stored in the case base. A case contains one’s own
and one’s opponent’s betting pattern for a hand and
the opponent’s hand strength shown at the showdown.
Algorithm 3: Case-based Decision with Bucketing.
Perceive situation s
c
s
= createCase(s)
if ∃C ⊂ CB with |C| > n : ∀c ∈ C : c ≈ c
s
then
∀c ∈ C : checkOpponentBucket(c)
return pt(r,c, f)(ownBucket,opponentBuckets)
else return null
end if
This hand strength is represented by a correspond-
ing bucket. In addition to the heuristic decision mak-
ing process for playing a hand, the case base can be
checked for similar cases corresponding to the hand
that is currently being played. Based on the oppo-
nent’s hand strength at the showdown in similar cases,
the case-based decision unit influences the probability
distribution of the resulting probability triple. This
helps to exploit and to adapt similar patterns of the
opponent’s play. A more complex case-based reason-
ing is used by the bot CASPER (Watson and Rubin,
2008) and SARTRE (Rubin and Watson, 2009).
Algorithm 3 shows the procedure of the case-
based decision process with bucketing. First, a case
c is created for a playing situation s that is perceived
by PLICAS. If there are more than n ∈ N cases stored
in the case base that are similar to c, the algorithm
checks each of these cases with respect to the behav-
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
68

          














  
    
 
! "
# 
$!%
$
Figure 4: Range model of the PLICAS poker bot.
ior that is stored in the opponent modeling buckets. In
order to do this, a similarity relation c
i
≈ c
j
is defined
for the cases c
i
,c
j
∈ C. A similarity for a case (situ-
ation) is given if the opponent takes the same action
pattern like for another situation. For all current states
of the game the opponent’s buckets in the correspond-
ing situation are checked. A better average bucket of
the opponent leads to a higher probability of folding
for PLICAS. A new case is put into the case-base if
it was played and recorded until showdown. A proba-
bility triple is generated based on the opponent’s hand
strength observed for playing situations with similar
hands (which have been recorded in previous games)
and the own hand strength in the current situation.
4.2.3 Bluff Unit
Although bluffing is not a part of a loss minimizing
pseudo-optimal strategy it can be integrated into the
player’s strategy to maximize the profit. An opponent
with a pseudo-optimal strategy plays an ε-Nash equi-
librium strategy where ε is an approximation factor
to the theoretical Nash equilibrium. As this opponent
can never reach a real Nash equilibrium PLICAS can
adapt to this strategy and take advantage of the insta-
bility factor ε.
The bluff unit provides the ability to determine
whether and how probable PLICAS should play a
bluff
9
. A situation where this can be used profitably
is the first action on the flop. In correspondence with
9
Our case: getting the opponent to fold the better hand.
the opponent model, PLICAS knowsthe preflop range
of the opponent and is able to derive the probability
that the opponent is holding a hand he is willing to
continue playing with. As the counter-probability ex-
presses how probable it is that the opponent will fold
to a bet, PLICAS can use this probability to determine
its own optimal bluffing frequency. These probabili-
ties are calculated by simulating all possible preflop
hand ranges at a big number of random flops. This
simulation approximates the probability that a start-
ing hand and the flop form a playable hand. Fig. 4
shows these probabilities as a function of the preflop
hand range. The blue curve represents the probability
of a playable hand. The probability is the disjunction
of the probabilities for holding a pair or better
10
(red
curve), two overcards (light blue curve), a flush draw
(green curve) or a straight draw (purple curve).
11
The
number of outs
12
determines how probable it is that
these hands will improve at the turncard. As the def-
inition of a playable hand can vary amongst different
players the probabilities are not always precise. PLI-
CAS accesses these previously simulated probabilities
in the form of a lookup table.
10
Including three of a kind, flush, straight or a better
hand.
11
A draw is a situation where a card is missing for flush /
straight. 2 overcards have a higher rank than all board cards.
12
A card which is still in the deck and can improve the
player’s hand is called an ‘out’.
PLICAS - A Texas Hold'em Poker Bot
69

-5000
0
5000
10000
15000
20000
25000
30000
35000
40000
Plicas (static) Match 1
Hands played
Small Blinds won















-5000
0
5000
10000
15000
20000
25000
30000
35000
40000
Plicas (static) Match 2
Hands played
Small Blinds won












-5000
0
5000
10000
15000
20000
25000
30000
35000
40000
Plicas (dynamic) Match 1
Hands played
Small Blinds won
















-5000
0
5000
10000
15000
20000
25000
30000
35000
40000
Plicas (dynamic) Match 2
Hands played
Small Blinds won












Figure 5: Simulation results of PLICAS (static (up) and dynamic (down)) vs. dpp.
4.2.4 Dynamic Postflop Aggression Control
As aggression describes the proportion of raises and
calls of a player, one’s own aggression should vary
between different opponent types. Against very ag-
gressive opponents (maniacs) a more passive play is
useful whereas being aggressive should be preferred
against very passive players (calling stations). In
addition to the opponent’s aggression, the dynamic
postflop aggression control (DPAC) also considers the
preflop range of the opponent. A tight range yields a
higher probability of the opponent holding a playable
hand after the flop and thus a higher aggression. The
DPAC adjusts PLICAS’ aggression in order to maxi-
mize profit against the opponent’s strategy. PLICAS’
strategy is modified by an intentional variation of the
original strategy based on observations of the oppo-
nent’s aggression and preflop ranges. This variation
is realized by a modification of the bucket mapping.
If PLICAS’s aggression is increased, hands can be put
into buckets representing a higher strength. If PLI-
CAS is supposed to play less aggressive, hands can
be put into a bucket representing a lower strength.
Bucket mapping is probabilistic to avoid exploitation.
5 EXPERIMENTS
The evaluation of PLICAS took place in two phases:
In a first step we used a bot called ‘dpp’, developed
by the University of Darmstadt, Germany
13
to per-
form pretests and in a second step PLICAS partici-
pated in the 2010 ACPC.
5.1 Pretests with the ‘dpp’ Poker Bot
Unfortunately the availability of poker bots outside
the ACPC is very limited. Due to this fact, we used
the freely available poker bot dpp for a first evalua-
tion of PLICAS. Dpp is a ‘mathematically fair’ poker
bot without opponent modeling which is specialized
on 3-Player Texas Hold’em Limit (it made the third
place in the 2009 ACPC). Despite the fact that dpp
is playing an ε-equilibrium strategy and has no op-
ponent modeling module, it can be considered as a
good initial benchmark to investigate the impact of
PLICAS’ dynamic units on its performance.
The framework used for the simulations is the
poker server of the ACPC. A poker match comprises
100, 000 hands including a rematch of the same size.
In a rematch exactly the same hands are played but
with switched positions.
Fig. 5 shows PLICAS’ performance against dpp
in the original match (left) and the rematch (right).
PLICAS has a winning rate of 0.302 SB per hand in
the first match and 0.377 SB per hand in the rematch.
The average winning rate in both matches is 0.340
SB per hand. Another run is performed while DPRC
and DPAC units of PLICAS are switched off. This
13
http://www.ke.tu-darmstadt.de/resources/poker
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
70

Table 2: Total bankroll results in BB per hand.
Rank Poker Bot Bankroll
1 PULPO 0.225± 0.003
1 Hyperborean.tbr 0.207± 0.002
2 Sartre 0.203± 0.002
3 Rockhopper 0.200± 0.002
4 Slumbot 0.199± 0.002
5 GGValuta 0.193± 0.003
6 Jester 0.164± 0.003
7 Arnold2 0.160± 0.003
8 GS6.tbr 0.139± 0.004
9 LittleRock 0.118± 0.003
10 PLICAS −0.46± 0.005
11 ASVP −0.320± 0.006
12 longhorn −0.144± 0.005
leads to a static playing style without adaptation to
the opponent’s strategy. In this case the winning rate
dropped to 0.179 SB per hand (Fig. 5, top) and to
0.250 SB per hand (Fig. 5, bottom) resulting in an
average winning rate of 0.215 SB per hand. Com-
paring the dynamic and the static version of PLICAS
the average winning rate drops by 37% from 0.34 to
0.215 SB per hand. The results show that PLICAS’
dynamic adaptive systems have a positive influence
on the winning rate. Even in a static standard play-
ing mode PLICAS is able to frequently win against an
average playing bot. After this initial evaluation of
PLICAS, we decided to participate in the ‘Heads-up
Limit Texas Hold’em’ category of the 2010 ACPC.
5.2 2010 Computer Poker Competition
The results of PLICAS in the 2010 ACPC are de-
picted in Tab. 2 and Tab. 3. Tab. 2 shows the total
bankroll results in big blinds (BB) per hand including
their variance.
14
All results are significant within a
95% confidence interval. Tab. 3 shows the ranking of
the poker bots after the runoff phase. Additionally,
literature related to the poker bots is given in Tab.
3, if available. While making the tenth place out of
twelve, PLICAS was not as successful as we initially
expected. However, one should consider that the most
poker bots in the 2010 competition have participated
in previous ACPC tournaments and therefore presum-
ably have an advantage in development.
In order to analyze the performance of PLICAS
we categorized the bots participating in the 2010
ACPC ‘Heads-up Fixed Limit’ competition accord-
ing to the decision methods used in the playing pro-
cess. The classification of the poker bots is given
in Tab. 4. The decision methods are discussed in
14
The rules and the results of the 2010 ACPC can also be
seen on: www.computerpokercompetition.org
Table 3: Ranking limit heads up runoff.
Poker Bot Literature
Rockhopper not available
GGValuta not available
Hyperborean (Johanson, 2007; Zinkevich et al., 2008)
Slumbot not available
PULPO not available
Sartre (Rubin and Watson, 2010; Rubin and Watson, 2009)
GS6.tbr (Gilpin et al., 2007)
Arnold2 not available
Jester not available
LittleRock not available
PLICAS this paper
ASVP not available
longhorn (Lockett and Miikkulainen, 2008)
Table 4: Decision methods of the poker bots.
Poker Bot Decision Method
PULPO learning, ε-equilibrium
Hyperborean min-regret, ε-equilibrium
Sartre case-based reason., opponent model
Rockhopper not available
Slumbot fictitious play, ε-equilibrium
GGValuta not available
Jester min-max , bucketing, ε-equilibrium
Arnold2 min-regret, simulation, ε-equilibrium
GS6.tbr bucketing ε-equilibrium
LittleRock regret-min., bucketing, ε-equilibrium
PLICAS case-based reason., bucketing,
learning, simulation, opponent model
ASVP learning, simulation, opponent model
longhorn learning, opponent model
Section 3. It is interesting to see that with the ex-
ception of SARTRE, the top ranking poker bots em-
ploy ε-equilibrium strategies (bots with unknown de-
cision methods are not considered here). Poker bots
using the ε-equilibrium strategy seem to have an ad-
vantage over opponent modeling bots unless the op-
ponent modeling bot is able to significantly exploit
the ε-deviations from the perfect equilibrium. From
this perspective PLICAS is the second best perform-
ing opponent modeling poker bot in the 2010 ACPC
‘Heads-up Fixed Limit’ competition. We believe that
the success of opponent modeling poker bots is di-
rectly related to the adaptivity of their playing strate-
gies and the quality of the case base. The SARTRE bot
used in the 2010 ACPC is a opponent modeling poker
bot in the third generation of development that might
be reason for a high adaptivity to the ACPC competi-
tors and can be seen as a source for its success.
PLICAS - A Texas Hold'em Poker Bot
71

6 CONCLUSIONS
We introduced the ‘Heads-up Texas Hold’em Fixed
Limit Bot’ PLICAS based on the computer poker
competition framework. Approaches such as case-
based reasoning, simulation-based bluffing, dynamic
range control, and automated aggression adaption
are integrated into PLICAS. Our research focuses on
the typical advantages of dynamic exploitative ap-
proaches aided by information gathering. The par-
ticipation in the 2010 AAAI Computer Poker Com-
petition (ACPC) showed that the overall performance
PLICAS has a lot of room for improvement. However,
in a differentiated analysis of the 2010 ACPC results,
we find that the performance of poker bots that oper-
ate by using a ε-equilibrium strategy is mostly supe-
rior to poker bots that use opponent modeling strate-
gies. From this point of view, PLICAS, is the sec-
ond best performing participant in the group of op-
ponent modeling poker bots. One way to improve
PLICAS’ performance is to evaluate and optimize
the direct impact of the functional components (bluff
unit, preflop range control, etc.) on the overall play-
ing strength of the poker bot, by switching them on
and off, while avoiding functional interferences of the
modules. With a lot of training and improvement of
the components PLICAS should be a real successful
poker bot in the 2011 ACPC competition.
REFERENCES
Billings, D., Burch, N., Davidson, A., Holte, R., Schauen-
berg, T., Schaeffer, J., and Szafron, D. (2003).
Approximating game-theoretic optimal strategies for
full-scale poker. In Proceedings of the International
Joint Conference on Artificial Intelligence (ICAI’03),
Las Vegas, Nevada, pages 661–668.
Billings, D., Papp, D., Schaeffer, J., and Szafron, D. (1998).
Opponent modeling in poker. In Proceedings of
the Fifteenth National Conference on Artificial In-
telligence (AAAI’98), Madison, WI, pages 493–499.
AAAI Press.
Billings, D., Pena, L., Schaeffer, J., and Szafron, D. (1999).
Using probabilistic knowledge and simulation to play
poker. In Proceedings of the Sixteenth National Con-
ference on Artificial Intelligence (AAAI’99), Orlando,
Florida, pages 697–703.
Davidson, A. (1999). Using artificial neural networks to
model opponents in texas hold’em. Res. Project Re-
view CMPUT 499, Poker Res. Group, Univ. of Al-
berta, CA.
Davidson, A., Billings, D., Schaeffer, J., and Szafron, D.
(2000). Improved opponent modeling in poker. In
Proceedings of the International Conference on Artifi-
cial Intelligence (ICAI’00), Las Vegas, Nevada, pages
493–499.
Gilpin, A., Sorensen, T. B., and Sandholm, T. (2007).
Potential-aware automated abstraction of sequential
games, and holistic equilibrium analysis of texas
hold’em poker. In Proceedings of the National Con-
ference on Artificial Intelligence (AAAI 2007) Vancou-
ver, Canada.
Hamilton, S. and Garber, L. (1997). Deep blue’s hardware-
software synergy. Computer, 30:29–35.
Johanson, M. (2007). Robust strategies and counter-
strategies: Building a champion level computer poker
player. Master’s thesis, University of Alberta.
Koller, D. and Pfeffer, A. (1997). Representations and so-
lutions for game-theoretic problems. Artificial Intelli-
gence, 94:167–215.
Kuhn, H. W. (1950). Simplified two-person poker. In Kuhn,
H. W. and Tucker, A. W., editors, Contributions to the
Theory of Games, volume 1, pages 97–103. Princeton
University Press.
Lockett, A. and Miikkulainen, R. (2008). Evolving oppo-
nent models for texas hold’em. In Proceedings of the
2008 IEEE Conference on Computational Intelligence
in Games. Perth, 2008. IEEE.
Nash, J. F. and Shapley, L. S. (1950). A simple 3-person
poker game. In Kuhn, H. W. and Tucker, A. W., edi-
tors, Contributions to the Theory of Games, volume 1,
pages 105–116. Princeton University Press.
Neumann, J. V. and Morgenstern, O. (1944). Theory of
Games and Economic Behavior. John Wiley.
Rubin, J. and Watson, I. (2009). A memory-based ap-
proach to two-player texas hold’em. In Proceedings of
the 22nd Australasian Joint Conference on Advances
in Artificial Intelligence AI’09, Melbourne, Australia,
pages 465–474. Springer.
Rubin, J. and Watson, I. (2010). Similarity-based re-
trieval and solution re-use policies in the game of
texas hold’em. In Proc. of the 18th Int. Conference
on Case-based Reasoning, ICCBR 2010, Alessandria,
Italy, pages 465–479.
Schaeffer, J. (1997). One jump ahead: challenging human
supremacy in checkers. Springer, NY, USA.
Schauenberg, T. (2006). Opponent modeling and search in
poker. Master’s thesis, University of Alberta, Depart-
ment of Computing Science, Edmonton, Alberta.
Sklansky, D. (1997). Hold’em Poker: A Complete Guide to
Playing the Game. Two Plus Two Publishing, Hen-
derson, NV, USA.
Southey, F., Bowling, M., Larson, B., Piccione, C., Burch,
N., Billings, D., and Rayner, C. (2005). Bayes’ bluff:
Opponent modelling in poker. In Proceedings of the
Twenty-First Conference on Uncertaintyin Artificial
Intelligence (UAI), pages 550–558.
Watson, I. and Rubin, J. (2008). Casper: a case-based
poker-bot. In Proceedings of the 21st Australasian
Joint Conference on Artificial Intelligence AI’08,
Auckland, New Zealand, volume 5360 of Lecture
Notes in Computer Science, pages 594–600. Springer.
Zinkevich, M., Johanson, M., Bowling, M., and Piccione,
C. (2008). Regret minimization in games with incom-
plete information. In Advances in Neural Information
Processing Systems 20 (NIPS), pages 1729–1736.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
72