INTER-MODEL CONSISTENCY BETWEEN UML STATE MACHINE

AND SEQUENCE MODELS

Yoshiyuki Shinkawa

Department of Media Informatics, Ryukoku University, 1-5 Seta Oe-cho Yokotani, Otsu, Shiga, Japan

Keywords:

UML, Model Consistency, Colored Petri Nets.

Abstract:

UML state machine diagram and sequence diagram represent a system or software from contrastive two view-

points, namely part and whole. If these diagrams depict the same system, they must be consistent with each

other. However, UML does not provide us with an appropriate way to evaluate the consistency between the

models drawn by these different diagrams. This paper reveals the interrelationships between state machine

and sequence diagrams based on the ordering of method invocations, which determine the behavior of them.

Focusing on these relationships, two criteria are introduced to evaluate the consistency. The evaluation is per-

formed using Coloured Petri Nets (CPN) so that both diagrams are expressed and compared in the same form,

with the same syntax and semantics.

1 INTRODUCTION

UML state machine diagram and sequence diagram

are two of the most used diagrams in modeling the be-

havioral aspects of a system to be developed. While

the former mainly expresses the behavior of individ-

ual object participating in the system, the latter deals

with the behavior of the system in the form of inter-

actions between these objects. These two kinds of di-

agrams can be regarded to have a part-whole relation-

ship, and therefore they must be consistent with each

other.

However, if these diagrams are used indepen-

dently to model the objects and the system, it is difﬁ-

cult to maintain consistency between the models writ-

ten using these different diagrams

. If there are in-

consistencies between the above models, the resultant

system would include various problems, e.g. unex-

pected malfunctions.

One of the reasons for this difﬁculty is that no ap-

propriate ways are provided by UML to evaluate the

consistency between these models (Egyed, 2006), and

it seems to be caused by expressive diversity and in-

sufﬁcient formalization of UML.

Various efforts have been made to formalize UML

In this paper, we call a model written using a speciﬁc

UML diagram as diagram-name + models, e.g. a sequence

model means a model written by UML sequence diagram.

for more rigorous speciﬁcation and veriﬁcation us-

ing diverse formal techniques, which include process

algebra (Fischer et al., 2001), formal speciﬁcation

languages like Z (Amalio and Polack, 2003), VDM,

(Lausdahl et al., 2009) or B (Snook and Butler, 2008),

model checking (Knapp and Wuttke, 2006), and Petri-

Nets (Garrido and Gea, 2002). These formal tech-

niques examine the structure, functionality, and be-

havior of the models written by UML diagrams pre-

cisely, and express the model semantics in their own

syntaxes.

On the other hand, much fewer efforts have been

made for inter-model relationships written by differ-

ent UML diagrams, such as the relationship between

UML state-machine models and sequence models. In

order to evaluate the inter-model consistency between

different UML models, we have to formalize not only

the internal structure of each model, but also the in-

terrelationships between them.

This paper presents a formal and systematic

way to evaluate inter-model consistency between the

above two kinds of UML models using Colored Petri

Nets (CPN) as a formalization technique. The paper

is organized as follows. In section 2, interrelation-

ships between the models are examined and revealed.

Section 3 discusses the transformation of UML state

machine and sequence models into CPN models. Sec-

tion 4 presents how the transformed CPN models are

evaluated to determine whether they are consistent.

135

Shinkawa Y..

INTER-MODEL CONSISTENCY BETWEEN UML STATE MACHINE AND SEQUENCE MODELS.

DOI: 10.5220/0003474001350142

In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 135-142

ISBN: 978-989-8425-77-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 INTERRELATIONSHIPS

BETWEEN THE MODELS

State machine and sequence models represent the be-

havior of a system from different viewpoints, based

on different model components. Therefore, we ﬁrst

have to identify the commonality between these mod-

els. We focus on the states of objects for this com-

monality.

In object oriented approaches, each object can

have states which are externally observable. At high

abstraction levels, these states are recognized as the

observable transitory properties of an object such as

appearances, dimensions, or activities currently per-

formed by the object. On the other hand, at more con-

crete levels, they are expressed as a value or a set of

values of the variable or variables in the object.

In order to make the discussion precise, we adopt

the latter interpretation of the states, and deﬁne them

as follows.

1. Let Ω be an object, including the variables

X = {x

,··· ,x

} for its attributes, each of which

is associated with the value space X

= dom(x

2. For a sub-domain S ⊆ X

× · · · × X

, if the two

tuples of values

,··· ,a

) ∈ S ⊆ X

× ···× X

,··· ,b

) 6∈ S ⊆ X

× ···× X

are externally distinguishable, and the distinction

is meaningful from an application viewpoint, S

forms a state S of the Ω.

3. The collection of such sub-domains deﬁnes a set

of the states Σ = {S

,··· ,S

}, where S

is a sub-

domain that is recognized as a state.

This deﬁnition relates a state of an object with a sub-

domain of the variables in the object. Such a sub-

domain can be deﬁned by a logic formula with pred-

icates. For example, if the temperature and humidity

of an object Room are represented by the variables x

and y respectively, and the state uncomfortable is de-

ﬁned by the sub-domain

S = {(x, y)|x > 30, y > 60} ∪ { (x, y)|x ≤ 10}

the state is represented as a logic formula

P(x,y) =



G(x,30) ∧ G(y, 60)



∨ ¬G(x,10)

where G(u,v) is the predicate, meaning u is greater

than v. Even though there could be many different

forms of a logic formula, there can be a unique prenex

conjunction normal form (PCNF), that is, the formula

written as a string of quantiﬁers (∀ and ∃), followed

by a conjunction of clauses.

Assuming each state in a state machine model rep-

resents such a state, a state transition

ε [ γ ] / α

−−−−−→ S

means the update of the variables by the action α,

when the guard γ holds. The symbol ε represents an

event triggering the transition. The above action α is

implemented as a method of the object, if the state

variables are fully encapsulated. Therefore, in such a

situation, a series of state transitions correspond to a

series of method invocations, each of which updates

the values of the state variables.

On the other hand, a sequence model represents

the interactions between lifelines in the form of mes-

sage passing. These lifelines can represent various

concepts and entities, e.g. classes, objects, actors, or-

ganizations, or other participants to the system to be

modeled.

In order to identify the interrelationships between

state machine and sequence models, both models

must have the common components, therefore we re-

gard the lifelines as objects. In this interpretation, a

receiving event occurrence represents a method invo-

cation in a sequence model.

One of the ways to express the behavior of a se-

quence model is to show the series of messages ex-

changed between lifelines. Regarding the lifelines

as objects, this series also represents the series of

method invocations. This series can be deﬁned for

the whole system or for a speciﬁc object, by extract-

ing the method invocations along the lifeline.

From the discussion so far, two series of method

invocations can be obtained for the same object, one

from a state machine model, and the other from a

sequence model. Therefore, by reﬁning these mod-

els appropriately to make these two series consist of

the same set of the methods, they can be a measure

to deﬁne the interrelationships between the two mod-

els. One of the differences between these two series

is that the sequence model might include the mes-

sages not affecting the states of the object. A typi-

cal such a message is an inquiry message, which only

returns some information without updating the state

variables.

Taking the above difference into account, the

inter-model consistency between state machine and

sequence models from a method invocation viewpoint

is deﬁned as follows.

1. Let A = a

···a

and B = b

···b

be the ob-

tained series of method invocations from state ma-

chine and sequence models respectively for the

same object.

2. Remove such methods from B that do not occur in

A , and let C = c

···c

be the remainder series

of B .

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

136

3. C must occur in A as a partial series of method in-

vocations, since C represents the series of method

invocations updating the states of the belonging

object.

The above series are not so easily obtained be-

cause of complicated structures of state machine and

sequence models. In order to identify and examine

these series automatically, we use Colored Petri Nets

(CPN) and CPN Tools (Jensen and Kristensen, 2009).

Before discussing the usage of them, we introduce an-

other consistency criterion based on the states of ob-

jects.

Unlike state machine models, sequence models

are scarcely founded on the concept of states. How-

ever, there are several points in a sequence model

where we can recognize the states. One is a state in-

variant located on a lifeline, and the other is a guard

that is occurred in some combined fragments like alt

and loop.

While the guards only control the sequence of

message passing, and might be true or false, the state

invariants represent the conditions that have to be sat-

isﬁed at speciﬁc points in the sequence model, and

must be true. Therefore, state invariants are eligible

to evaluate the consistency.

Since the method invocation sequence in a se-

quence model is matched with that of the correspond-

ing state machine model, the states in the state ma-

chine model can be injected into the sequence model,

so that we can identify the states at the receiving event

occurrences where the corresponded messages arrive

at.

By this injection, each lifeline is partitioned into

zones associated with the states as shown in Figure 1.

As stated above, the states can be expressed in

the form of logical formulae with state variables, and

therefore we can assign these logical formulae to the

above zones. On the other hand, state invariants are

the assertions on the states, either object or system

states, and can be expressed in the form of logical for-

mulae.

Since each state invariant is located at a particular

point on a lifeline, it belongs to one of these zones as-

sociated with a logical formulae. Therefore, the state

invariant must not conﬂict with the logical formula of

the zone it belongs. Let the state invariantbe S(~u), and

the logical formula of the associated zone be P(~x),

P(~u) → P(~x)

must hold, where~u and~x represent the state variables.

These state injection and state invariant consis-

tency are also implemented by CPN.

3 MODEL COMMONIZATION

WITH CPN

Colored Petri Nets (CPNs) are one of the extensions

of regular Petri nets, which can express the structure,

behavior, and functionality simultaneously for vari-

ous systems. CPN is formally deﬁned as a nine-tuple

CPN=(P, T, A, Σ, V, C, G, E, I) , where

P : a ﬁnite set of places.

T : a ﬁnite set of transitions.

(a transition represents an event)

A : a ﬁnite set of arcs P∩ T = P∩ A = T ∩ A =

Σ : a ﬁnite set of non-empty color sets.

(a color represents a data type)

V : a ﬁnite set of typed variables.

C : a color function P → Σ.

G : a guard function T → expression.

(a guard controls the execution of a transition)

E : an arc expression function A → expression.

I : an initialization function : P → closed expression.

3.1 Transforming State Machine

Models into CPN

State machine models and CPN models show similar

properties, since both originated from ﬁnite automata.

The structural relationships between these two mod-

els are as follows.

1. Each state in a state machine model corresponds

to a place in a CPN model. The color associated

with the place is composed of the types of the state

variables.

2. A state transition corresponds to a transition put

between two places that reﬂect the source and des-

tination states of the state machine

For a label on the state transition, which is de-

noted as ”event[guard]/action”, the event and guard

are transformed into a guard function of the associ-

ated CPN transition, while the action is transformed

into the outgoing arc function that updates the token

value.

Based on the above structural correspondences, it

is required to build a behaviorally equivalent CPN

model to a given state machine model, in order to

commonize state machine and sequence models.

Unlike simple ﬁnite automata, UML state ma-

chine models can include complicated control struc-

tures and functionality, and they must be embedded

in the CPN models. These can be expressed in the

form of CPN as follows.

INTER-MODEL CONSISTENCY BETWEEN UML STATE MACHINE AND SEQUENCE MODELS

137

State Machine Model

for the Object L1

Sequence Model Including

the Object L1 as a Lifeline

e1[g1]/a1

e2[g2]/a2 e3[g3]/a3

Injected State

Figure 1: State Injection into Sequence Model.

[Initial State]

An initial state is expressed in CPN as a place with

initial marking, and with no incoming arcs.

[Final State]

A ﬁnal state is expressed as a place with no outgo-

ing arcs.

[Composite State]

A composite state includes another state machine

model inside, and expressed as a substitution transi-

tion in a CPN model, since this state itself can be re-

garded as a process or behavior.

[Submachine State]

A submachine state is an inserted state ma-

chine, and simply expressed using a hierarchical CPN

model.

[Entry Point]

An entry point is an alternative initial state, and

expressed in the same way as an initial state in

CPN. The initial marking of the CPN model controls

whether it becomes initial state.

[Exit Point]

An exit point is an alternative ﬁnal state, and ex-

pressed in the same way as a ﬁnal state. If entry or an

exit point is a submachine state, they are expressed as

a port-socket pair in CPN.

[Fork and Join Pseudo State]

A fork pseudo state initiates a parallel state tran-

sitions, whereas a join pseudo state merges them into

a single one. These pseudo states can be expressed as

splitting and merging transitions with multiple places

in CPN.

[Choice and Junction Pseudo States]

These pseudo states express control branches.

While the former realizes a dynamic branch, and

only one state transition is allowed, the latter real-

izes a static branch, and multiple state transitions

are possible. A choice pseudo state is simply im-

plemented by CPN using competing transitions with

guards. On the other hand, a junction pseudo state

is rather tricky, which is implemented using a inter-

mediate place and arc functions that provide empty

tokens if the guards fail. Figure 2 shows the junction

pseudo state with two incoming and three outgoing

state transitions, which is transformed into the CPN

model with the intermediate place “P”. The arc func-

tion “a

(i = 3,4,5)” are the CPN/ML functions

if g

then x else empty

where g

is the guard for the transition “Ti” and x is

the variable for the token.

S1 S2

S3 S4

P1 P2

T1 T2

T3 T4 T5

P3 P4 P5

a3 a4 a5

[g3]

[g4]

[g5]

[g3] [g4] [g5]

Figure 2: Junction Pseudo State.

[Shallow and Deep History Pseudo States]

These pseudo states provide restart capability for

composite states. In CPN models, a substitution tran-

sition that is equivalent to the composite state must

also be restartable. This restart mechanism is realized

by appending three places, each of which represents

exit, checkpoint, and re-entry respectively, along with

an escape transition for each place that represents the

state.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

138

Shallow and deep are distinguished from each

other whether the above mechanism is nested or not.

3.2 Transforming Sequence Models into

CPN

There are two possible implementations of sequence

models by CPN.

One is a structure based implementation, which

assigns a place for each lifeline, and assigns a transi-

tion with an incoming arc to it for each incoming mes-

sage to the lifeline. We can easily transform a given

sequence model into CPN model using these simple

rules, however the resultant CPN model is not com-

patible with state machine models, since no concepts

of states are included.

The other is a state based implementation, which

takes the states of objects into account. As discussed

in Section 2, an injected state is deﬁned for each

incoming message to a lifeline, of which operation

name occurs as an action name in the state machine

model for the object that the life line represents.

Therefore, a CPN model consisting of the places

for these injected states, and of the incoming arc with

a transition to the above each place, reﬂects this im-

plementation. Such a CPN model can basically be

transformed in the same way as state machines. How-

ever, sequence models could form more complicated

structure than state machine models using combined

fragments. The treatment of these combined frag-

ments is as follows (Shinkawa, 2006).

[Alternative and Option Fragments]

An alternative and option fragments, designated

by alt and opt tag, represent case and if - then struc-

tures respectively, and implemented by CPN using as

many transitions as the number of regions in the frag-

ment. Each transition is assigned a guard equivalent

to the guard of corresponded region.

[Loop Fragment]

A loop fragment, designated by loop tag, repre-

sents an iterative process, and is implemented using

two conﬂicting transitions for iteration and exit re-

spectively.

[Parallel Fragment]

A parallel fragment, designated by par tag, rep-

resents concurrent message passing between the life-

lines, and is interpreted as concurrent state transitions

in the state based implementation. This fragment is

expressed in CPN using a transition splitting one in-

coming arc into multiple outgoing arcs.

[Break Fragment]

A break fragment, designated by break tag, is used

to terminate the message passing in the outer frag-

ment, to which the break fragment belongs. Since

the fragment is controlled by a guard, it can be im-

plemented as a transition with the equivalent guard,

which puts a token into the place outside the fragment.

[Critical Fragment]

A critical fragment, designated by critical tag,

represents a message passing process that must be

performed exclusively, and usually used within a par-

allel fragment. This fragment is expressed in CPN us-

ing a place with a lock token. The locking mechanism

works as follows.

1. The ﬁrst transition in the fragment gets the lock

in the above place, and the transition immediately

after the fragment return the lock.

2. Each transition that conﬂicts with the critical frag-

ment refers to this place, that is, bidirectional arcs

are drawn between the transition and the place.

[Weak Sequencing Fragment]

A weak sequencing fragment, designated by seq

tag, deﬁnes the ordering of messages as follows

(OMG, 2010).

1. The ordering of OccurrenceSpeciﬁcations within

each of the operands are maintained in the result.

2. OccurrenceSpeciﬁcations on different lifelines

from different operands may come in any order.

3. OccurrenceSpeciﬁcations on the same lifeline

from different operands are ordered such that

an OccurrenceSpeciﬁcation of the ﬁrst operand

comes before that of the second operand.

This fragment reduces to a par fragment if all the

operands include disjunct sets of lifelines interacting

together. Therefore, when tranforming it into CPN,

we ﬁrst regard it as par fragment, then add the order-

ing restrictions to it. The detailed implementation is

as follows.

1. Build the CPN model for the seq fragment as par

fragment.

2. Derive all the ordering constraints ( ˆm

i, j

≺ ˆm

i+1,k

)

between (i)th and (i + 1)th operands or regions

and P

i+1

, where ˆm

i, j

and ˆm

i+1,k

represent the

receiving event occurrences for the message m

i, j

and m

i+1,k

in the operand P

and P

i+1

respectively.

3. Draw an additional arc between P ( ˆm

i, j

) to

T ( ˆm

i+1,k

), and modify the incoming arc function

of the P ( ˆm

i, j

) so that an extra token for the tran-

sition T ( ˆm

i+1,k

) is provided. In addition, modify

the guard of T ( ˆm

i+1,k

) for this extra token. P ( ˆm)

and T ( ˆm) represent the place and transition asso-

ciated with the receiving event occurrence ˆm.

For example, in Figure 3, the order of the re-

ceiving event occurrences, which are denoted by the

names of messages, must satisfy m

≺ m

and m

≺

INTER-MODEL CONSISTENCY BETWEEN UML STATE MACHINE AND SEQUENCE MODELS

139

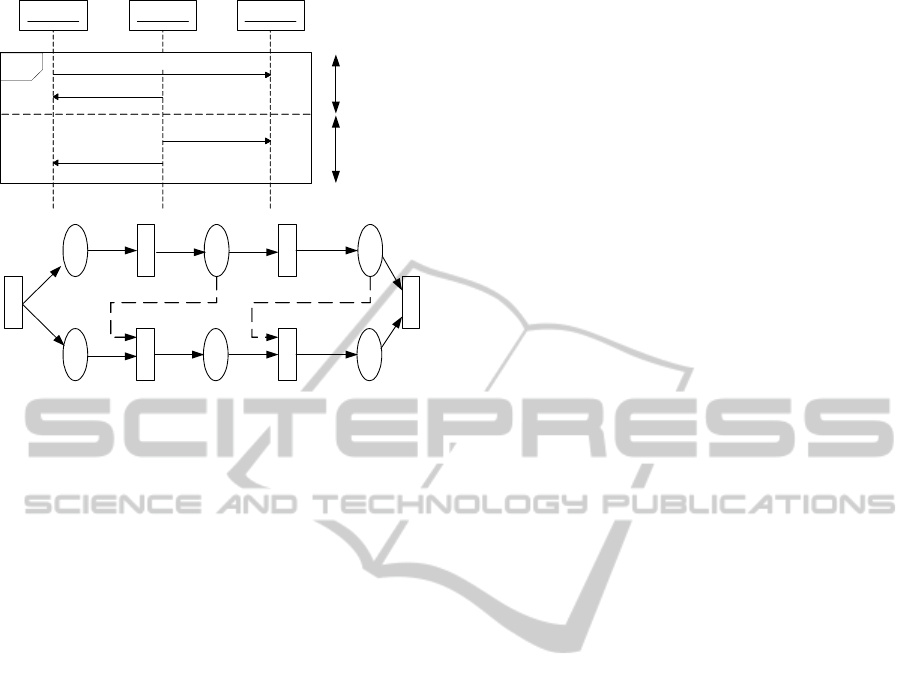
Object 1 Object 2

seq

Object 3

Operand 1

Operand 2

Figure 3: Weak Sequencing Fragment.

, and these constraints can be embedded into the

CPN model for par fragment using the additional arcs

shown by the dashed arrows. In addition, the place m

and m

must include the additional tokens for this se-

quence control, which can be implemented by the arc

functions toward them.

[Other Combined Fragments]

There are other supplementary combined frag-

ments like strict, assertion, ignore, consider, and

negation deﬁned in a UML sequence model, however

they do not affect the essential behavior of the model,

and therefore we do not take them into account.

By applying the above process to a sequence

model, we can obtain a behaviorally equivalent CPN

model from the method invocation viewpoint. In ad-

dition, a CPN model for a speciﬁc lifeline or an object

can be obtained by extracting the places representing

the receiving event occurrences for the object, with

the incoming arcs. To make the complete CPN model

from these elements, a dummy initial place and tran-

sitions are added with the appropriate arcs.

4 EVALUATING THE

CONSISTENCY

For discussing the inter-model consistency between

models, we posit the following assumptions, which

seem reasonable for practical applications.

• A state machine model is built for each object to

represent its behavior under all situations.

• A sequence model is built for a system using the

above objects as lifelines. The model represents a

speciﬁc individual application.

The CPN models obtainable through the proposed

transformation process are

• CPN model for each object from a state machine

model. The model is referred to as a state machine

CPN model.

• CPN model for a system including the above ob-

jects from a sequence model. The model is re-

ferred to as a sequence CPN model.

• CPN model for a object from a sequence model,

which occurs as a lifeline. The model is referred

to as a lifeline CPN model.

As discussed in section 2, the inter-model consistency

is deﬁned in the two ways. One is based on the or-

dering of method invocations, and the other is based

on the state injection. We refer the former as method

based consistency and the latter as state based consis-

tency.

[Method Based Consistency]

This consistency requires the series of method in-

vocations occurring in a sequence model along a spe-

ciﬁc lifeline must occur in the corresponding state

machine model. Formally, the consistency is deﬁned

as follows.

1. Let P and Q be a state machine CPN model

and the corresponding lifeline CPN model respec-

tively.

2. Let trace(P) and trace(Q) be the series of arc

functions obtained through the execution of the

model P and Q.

3. The model P and Q are consistent if trace(P) in-

cludes trace(Q) as a substring.

The above trace(P) and trace(Q) can be expressed in

the form of integer lists by assigning a unique posi-

tive number to each outbound arc from a transition.

We refer to such lists as trace lists and the evaluation

seems simple. However, if the models include con-

current method invocations using the fork/join pseudo

states in the state machine model, or the par com-

bined fragments in the sequence model, the ordering

of the method invocations does not uniquely deter-

mined, and therefore the above criterion is not always

adequate. In order to deal with such a situation, we

use a separate trace list for each process performed

parallelly, along with a unique negative number as-

sociated with each parallel processing. The detailed

procedure is as follows.

1. Until the ﬁrst parallel processing occurs, use a sin-

gle trace list [−1,a

,···], where −1 is the neg-

ative number assigned to this single processing,

and a

is a positive number that represents an arc

or a method invocation.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

140

2. Each time a transition splits the process into n par-

allel processes, the currently used trace list ends

with a unique negative number q less than the cur-

rent one p, and an independentlist is used for each

parallel process, which begins with the above neg-

ative number q.

3. When m parallel processes are merged into a

single process, the m independent trace lists are

switched to the one for the previous common pro-

cess, from which these m processes are split.

The above procedure suggests that each trace list is

composed in the form of

,··· , p

,···]

where p

is the unique negative number assigned to

the process that uses the list, and is referred to as a

“split ID”. This ID is propagated as a part of a token.

However, it is rather complicated to identify the

above common process in the step 3, as depicted be-

low.

1. Let Q = { q

,··· ,q

} be a set of the split IDs as-

signed to the n processes to be merged (s ≤ m).

2. Compose a set of split IDs P

= {p

} for each q

where p

is the ﬁrst element of a trace list in the

form of [p

,··· , p

ij− 1

] that satisﬁes (p

= q

These lists must be identiﬁed until p

becomes

−1 from the deﬁnition of a trace list.

3. Let R = {r

,··· ,r

} be a set of the split IDs

which satisfy r

< r

··· < r

= −1 and

∀(1 ≤ i ≤ m)∀(1 ≤ j ≤ v)[r

∈ P

]

4. The above r

is the split ID assigned to the origi-

nal common process that splits the n parallel pro-

cesses to be merged, since when the original com-

mon process split it into processes, they are as-

signed the same negative number.

In order to make the comparison possible between

trace lists, we modify the original CPN models by

adding a special place to hold them, which is referred

to as trace holder. Each transition in the original CPN

model is connected to the trace holder with a new arc

to append the information of the arc functions that the

transition performed. The color set assigned to the

trace holder is a list of the trace lists so that we can ac-

cess all the trace lists by a single arc. Figure 4 shows

simpliﬁed structure of a CPN model with the place

holder.

Since the method based consistency is deﬁned for

an object that occurs in both the state machine and

sequence CPN models, the CPN models to be com-

pared is a state machine CPN model and a lifeline

CPN model for the same object. The detailed com-

parison algorithm is as follows.

CPN-post

CPN-pre

Trace Holder

Figure 4: Trace Holder Place.

1. Let L = [λ

,λ

,··· ,λ

] and M = [µ

,µ

,··· , µ

]

be the lists of trace lists to be compared.

2. Identify the set of the trace lists in L

A = {

| ∀ j [hd

≤ hd λ

]}

which means the set of the trace lists that are as-

signed the least negative number.

3. Identify the set of the trace lists in M

B = {˜µ

| ∃

∈ A [butNeg

= butNeg ˜µ

]}

where “butNeg” is a ML function that is applica-

ble to an integer list to remove the negative ele-

ments in it. If there is no such B, the two models

are inconsistent.

4. For the sets of trace lists

L = L− A and

M = M −

B, repeat the steps until

L becoms the empty set.

To make this consistency evaluation semi-automated,

several additional model componentsare needed. One

is a transition that marks the initial tokens to the given

CPN models. The second is a transition that receives

the lists of trace lists as the tokens from the CPN mod-

els to be evaluated. This transition examines these

lists of the trace lists whether they satisfy the consis-

tency criteria discussed above. The third is a place to

hold the evaluation results.

[State Based Consistency]

This consistency requires each state invariant lo-

cated on a lifeline must not conﬂict with the injected

state from the state machine model. Formally, the

consistency is deﬁned as follows.

1. Let S(~u) be the logic formula representing the in-

jected state of a zone where a state invariant I(~v) is

located, which is expressed in the form of a logic

formla.

2. S(~u) and I(~v) are consistent if S(~u) → I(~v) holds.

For the state based consistency evaluation, we

have to identify the state at the point where a state

INTER-MODEL CONSISTENCY BETWEEN UML STATE MACHINE AND SEQUENCE MODELS

141

invariant is located in the sequence CPN model. As

discussed above, each lifeline is divided into zones,

each of which is associated with a predicate logic for-

mula.

A place in a sequence CPN model represents a

receiving event occurrence in the original sequence

model, and this event occurrence belongs to one of the

above zones. Therefore, each place in a CPN model is

related to the state and its logic formula. In addition,

a place is also related to the state invariants reside in

the same zone.

Assuming a place in a sequence CPN model is re-

lated to a state S and a set of state invariants {T

L (S) → L (T

) must hold in our consistency deﬁni-

tion, where L (S) and L (T

) represent the logic for-

mulae associated with S and T

In order to examine the formula L (S) → L (T

we introduce two new transitions for the place associ-

ated with the T

. The guards for these transitions are



L (S) → L (T

)



and ¬



L (S) → L (T

)



respec-

tively. And a bidirectional arc is drawn between the

place and each of the transitions.

In addition, the transition with the guard



L (S) → L (T

)



is connected to an place for error

messages. In the case L (T

) requires extra variables

that the associated place does not provide, the addi-

tional bidirectionalarcs are drawn from the places that

can provide the required variables.

5 CONCLUSIONS

The inter-model consistency between UML state ma-

chine and sequence models was discussed in this pa-

per. Method invocations were used as the basic com-

mon elements of those both models, which deﬁne

the consistency criteria. We introduced two kinds of

inter-model consistency. The ﬁrst is the method based

consistency which assures the ordering of method in-

vocations is identical for the same object between

these two models. The second is the state based con-

sistency which conﬁrms the adequacy of the state in-

variants located in a sequence model, against the cor-

responding state machine models. The consistency

is evaluated using Colored Petri Nets (CPN) so that

the behavior of the both models is expressed and ob-

served in the same form, and is compared more rigor-

ously and precisely than UML.

This approach would be applied to other combina-

tions of UML diagrams, e.g. state machine and activ-

ity diagrams, to evaluate inter-model consistency.

REFERENCES

Amalio, N. and Polack, F. (2003). Comparison of formal-

isation approaches of UML class constructs in z and

object-z. In 3rd international conference on Formal

speciﬁcation and development in Z and B, pages 339–

358. Springer-Verlag.

Egyed, A. (2006). Instant consistency checking for the

UML. In 28th International Conference on Software

Engineering, pages 381–390. ACM.

Fischer, C., Olderog, E., and Wehrheim, H. (2001). A CSP

view on UML-RT structure diagrams. In 4th Inter-

national Conference on Fundamental Approaches to

Software Engineering, pages 91–108. Springer-Verla.

Garrido, J. and Gea, M. (2002). A coloured petri net for-

malisation for a UML-based notation applied to co-

operative system modelling. In the 9th International

Workshop on Interactive Systems. Design, Speciﬁca-

tion, and Veriﬁcation, pages 16–28. Springer-Verlag.

Jensen, K. and Kristensen, L. (2009). Coloured Petri

Nets: Modeling and Validation of Concurrent Sys-

tems. Springer-Verlag.

Knapp, A. and Wuttke, J. (2006). Model checking of UML

2.0 interactions. In Workshops and Symposia at MoD-

ELS 2006, pages 45–51.

Lausdahl, K., Lintrup, H., and Larsen, P. G. (2009). Con-

necting UML and VDM++ with open tool support. In

the 2nd World Congress on Formal Methods, pages

563–578. Springer-Verlag.

OMG (2010). Uniﬁed Modeling Language Superstructure.

http://www.omg.org/spec/UML/2.3/Superstructure/PDF.

Shinkawa, Y. (2006). Inter-model consistency in UML

based on CPN formalism. In 13th Asia Paciﬁc Soft-

ware Engineering Conference, pages 411–418. IEEE.

Snook, C. and Butler, M. (2008). UML-B and Event-B: an

integration of language. In the IASTED International

Conference on Software Engineering, pages 336–341.

ACTA Press.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

142