MODELING AND ANALYSIS OF A POWER LINE

COMMUNICATION NETWORK SUBJECT TO CHANNEL

FAILURE

Shensheng Tang

Dept. of Engineering Technology, Missouri Western State University, St. Joseph, MO 64507, U.S.A.

Yi Xie

Dept. of Elec. and Comm. Engineering, Sun Yat-Sen University, Guangzhou, 510006, China

Keywords: Power line communication (PLC), Performance modeling, Markov Process, Channel failure.

Abstract: Power line communication (PLC) is a promising technique for information transmission using existing

power lines. We analytically model a finite-source PLC network subject to noise/disturbance and evaluate

its call-level performance through a queuing theoretic framework. The proposed PLC network model

consists of a base station (BS), which is located at a transformer station and connected to the backbone

communication networks, and a number of subscriber stations that are interconnected with each other and

with the BS via the power line transmission medium. An orthogonal frequency division multiplexing

(OFDM) based transmission technique is assumed to be used for providing the transmission channels in a

frequency spectrum. The channels are subject to failure during service due to noise/disturbance. When a

channel is in failure, its associated call will wait at the channel until the channel is recovered. We model this

process and determine the steady-state solution and derive several performance metrics of interest.

Numerical and simulation results are presented for the purpose of performance evaluation. The proposed

modeling method can be used for evaluation and design of future PLC networks.

1 INTRODUCTION

Power line communication (PLC) is a promising

technique for information transmission using

existing power lines. PLC technologies can be used

in an inside-building low voltage environment, a

short-distance medium voltage environment, or a

long-distance high voltage environment. Mixed

high-voltage, medium-voltage, and low-voltage

power supply networks could be bridged to form

very large networks for communications, as

alternative telecommunication networks.

The great advantage of PLC is that the power

lines exist in every home and every room. For

example, a computer would need only to plug a BPL

“modem” into any outlet in an equipped building to

have high-speed Internet access. Therefore, huge

cost of running wires such as Ethernet in many

buildings can be saved. However, there are still lots

of challenges for implementation in reality. Since

the power line network has originally been designed

for electricity distribution, rather than for data

transfer, the power line as communication channel

has various noise and disturbance characteristics,

resulting in an unreliable channel. Many factors,

such as channel attenuation, white noise, RF noise

from nearby radio transmitters, impulse noise from

electrical machines and relays, may cause the

channel unreliability.

In practice the impact of RF noise on a channel

can be reduced significantly with OFDM.

(Stantcheva, Begain, Hrasnica, and Lehnert, 2000).

Based on the measurements reported in

(Zimmerman and Dostert, 2002), the noise in the

power line communication channels is categorized

in five types, where the last type (i.e., asynchronous

impulsive noise) is the most unfavorable one and

makes more difficulties to the power line channels.

184

Tang S. and Xie Y..

MODELING AND ANALYSIS OF A POWER LINE COMMUNICATION NETWORK SUBJECT TO CHANNEL FAILURE.

DOI: 10.5220/0003475101840189

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 184-189

ISBN: 978-989-8425-55-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

The power spectral density of this type of noise can

reach values of more than 50dB above the

background noise.

Much research PLC has been developed in the

past a few years. The focused topics include MAC

(medium access control) protocols (Hrasnica and

Haidine, 2000), noise and channel modeling

(Zimmerman and Dostert, 2002), (Katayama,

Yamazato, and Okada, 2006), modulation and

multiple access techniques (Haring and Vinck,

2000), (Amirshahi, Navidpour, and Kavehrad,

2006), or modem design (Yu, Yu, and Lee, 2003). In

(Hrasnica and Haidine, 2000), some reservation

MAC protocols were proposed for the PLC network

which provides collision free data transmission. A

simulation model was developed for the study of the

PLC MAC layer that includes different disturbance

scenarios. In (Zimmerman and Dostert, 2002), it was

examined that the impulsive noise introduces

significant time variance into the powerline channel.

Spectral analysis and time-domain analysis of

impulsive noise were presented in details. In

(Katayama, Yamazato, and Okada, 2006), a

mathematically tractable model of narrowband

power line noise was introduced based on

experimental measurements. With the assumption of

Gaussian noise with instantaneous variance of a

periodic time function, the cyclostationary features

of power line noise can be described in close form.

The performance of the OFDM transmission

scheme corrupted by impulsive noise was analyzed

in (Haring and Vinck, 2000). It showed that the

Gaussian noise OFDM receiver in an impulsive

noise environment causes strong performance

degradation, and proposed an iterative algorithm to

mitigate the influence of the impulsive noise. In

(Amirshahi, Navidpour, and Kavehrad, 2006), the

bit error rate performance of the OFDM system

under impulsive noise and frequency selective

fading was analyzed and closed form formulas were

derived. In (Yu, Yu, and Lee, 2003), a PLC modem

applicable to central monitoring and control systems

was designed by using a multicarrier CPFSK

modulation with adaptive impedance matching.

All the above research was done at the link level

or component level. Very little research studied the

performance at the system level. In this paper, we

study the call-level performance of PLC networks at

the system level through through a queuing theoretic

framework. The proposed PLC network model

consists of a base station (BS), which is located at a

transformer station and connected to the backbone

communication networks, and a number of

subscriber stations (SSs) that are interconnected with

each other and with the BS via the power lines. An

OFDM based transmission technique is assumed to

be used for providing the transmission channels in a

frequency spectrum, which is divided into a set of

narrowband subcarriers (or subchannels). The

subchannels are subject to failure during service due

to the noise/disturbance on the power lines.

When a channel is in failure, its associated call

will wait at the channel until the channel is

recovered (i.e., the noise/disturbance is gone), then

the call continues its service. The failure events in

different subchannels are independent due to the flat

fading characteristic in each divided subchannel.

The remainder of the paper is organized as

follows. Section 2 presents the system description.

Section 3 develops a two-dimensional Markovian

model for performance analysis. Section 4 derives

several performance metrics of interest. Section 5

presents numerical and simulation results. Finally,

the paper is concluded in Section 6.

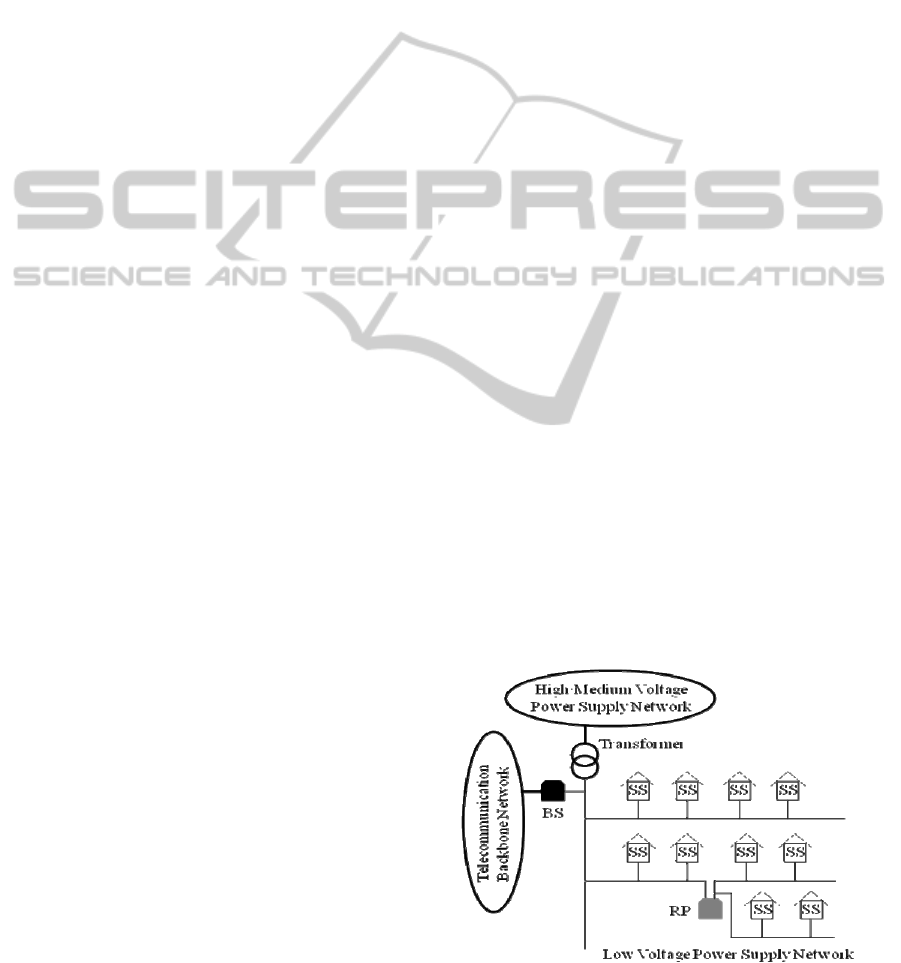
2 SYSTEM DESCRIPTION

Consider a PLC access network in the range of a

low-voltage power supply network, as shown in Fig.

1. It consists of a BS that is connected to a backbone

telecommunication network and a number of SSs

that are interconnected with each other and with the

BS via the power lines. The transformer station

distributes power to the covered low-voltage power

supply network and receives power from a medium-

voltage or high-voltage power supply network.

When an SS is located near the BS, the

communication can be organized directly between

the SS and the BS. Otherwise, one or more repeaters

(RPs) may be required inside the network to

compensate for signal attenuation.

Figure 1: A PLC network architecture.

MODELING AND ANALYSIS OF A POWER LINE COMMUNICATION NETWORK SUBJECT TO CHANNEL

FAILURE

185

The BS is an access point for communications

between an SS of the PLC network and a user of an

external network, and for communications between

the SSs inside the PLC network. The signal

transmission directions in a PLC network include

downlink — from the BS to the SSs and uplink —

from an SS to the BS. In the downlink, the BS sends

a transmission signal to all the SSs in the PLC

network. In the uplink, a signal sent by an SS can

not only be received by the BS, but also be received

by all other SSs. Hence, the PLC access network

holds a logical bus topology, where a set of SSs are

connected via a shared communication media —

power line, called bus. This type of network may

have problems when two or more SSs want to

transmit at the same time on the same bus. Hence,

some scheme of collision handling or collision

avoidance is required for communications, such as

carrier sense multiple access (CSMA) or an access

control by the BS. The latter is assumed here.

The OFDM is recommended by ITU-T G.hn as

the modulation scheme for PLC networks due to the

fact that it can cope with frequency selectivity (or

time dispersion) — the most distinct property of

power line channel, without complex equalization

filters. Moreover, OFDM can perform better than

single carrier modulation in the presence of

impulsive noise, because it spreads the effect of

impulsive noise over multiple subcarriers. The

available spectrum is divided into a set of

narrowband subcarriers (or subchannels), which are

overlapping in frequency and orthogonal in time.

We assume that these channels are all traffic

channels, without including any control channels.

The signalling control is assumed to be ideal and is

not discussed here.

As mentioned in Section 1, the impulsive noise

introduces significant time variance into the power

line channel, which indicates a high likelihood of bit

or even burst errors for digital communications over

power lines. The statistics of the measured

interarrival times of impulsive noise above 200ms

follows an exponential distribution. For this sake, in

(Hrasnica and Haidine, 2000), the channel was

modelled by a Markovian chain with two states, T

and T

off

, represented by two exponentially

distributed random variables, where T

denotes the

absence of impulses and the channel is available for

utilization, and T

off

denotes the duration that the

channel is disturbed by an impulse and no

information transmission is possible.

The BS knows about the occupancy status of the

channels. The BS allocates the available channels to

the requested calls from the SSs. When a requested

call arrives, it will enter the system if there is a

channel available; otherwise, it will be rejected.

Note that the channels are subject to failure

during service due to the noise/disturbance. The

failure events in different channels are independent

and identically-distributed (i.i.d.). When a channel is

in failure, the associated call will wait at the channel

until the channel is recovered. Once the failed

channel is recovered, the waiting call will continue

its service immediately.

3 PERFORMANCE ANALYSIS

For the above PLC network with N SSs and m traffic

channels, we assume that the arrival process of an

individual idle SS is a Poisson process with rate λ.

The channel holding time of a call is exponentially

distributed with mean 1/μ. We further assume that

each call occupies one channel for simplicity.

Due to noise/disturbance, the channel may be

subject to failure. We assume that the occurrence of

channel failures follows a Poisson process with rate

α, i.e., the interarrival time of the failure events

follows exponentially distributed with mean 1/α. In

each failure event, it is assumed that the remaining

duration (i.e., the recovery time) is exponentially

distributed with mean 1/β.

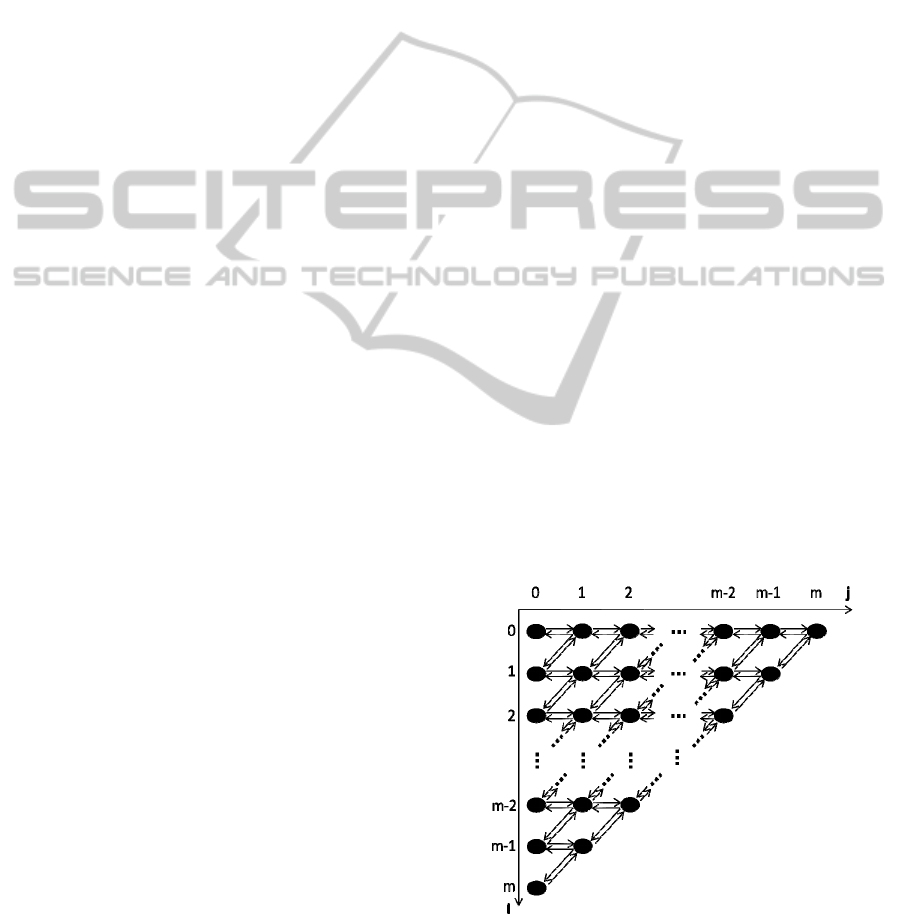
Let X(t) denote the number of failed channels at

time t. Similarly, let Y(t) be the number of calls

being served at time t. The process (X(t),Y(t)) is a

two-dimensional Markov process with state diagram

shown in Fig. 2 and state space

S = { (i, j) | 0 ≤ i ≤ m, 0 ≤ j ≤ m-i }.

Figure 2: The state diagram of the PLC network.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

186

We denote the transition rate from state

),( ji

)','( ji

','

and specify the different transition

rates as follows.

⎩

⎨

⎧

−<≤−≤≤−−

.,0

,0,10,)(

otherwise

imjmijiN

(1)

⎩

⎨

⎧

−≤≤−≤≤

−

.,0

,1,10,

otherwise

imjmij

(2)

⎩

⎨

⎧

−≤≤−≤≤

−+

.,0

,1,10,

1,1

otherwise

imjmij

(3)

⎩

⎨

⎧

−≤≤≤≤

+−

.,0

,0,1,

1,1

otherwise

imjmii

(4)

Let π(i, j) denote the steady-state probability that

the PLC network is at state (i, j). The global balance

equations of the system are given as follows:

,0,0

,)1)(1,1()1)(1,(

)1)(1,1()1)(1,(

])())[(,(

imjmi

jjijji

ijijiNji

ijjiNji

−<≤<≤

++−++++

+−+++−−−=

+++−−

απμπ

βπλπ

(5)

,,0

,)1)(1,1()1)(1,1(

)1)(1,(])()[,(

imjmi

ijijji

jiNjiijji

−=≤≤

+−++++−+

+−−

−

=++

βπαπ

(6)

where

)1,( =−i

),1( =− j

, and

),(

i >+

The above equations contain (m+1)(m+2)/2

unknowns, i.e., the probabilities

),( ji

with

mi ≤≤0

and

imj

−

≤≤0

. But there are only

m(m+1)/2 independent equations in the above

equations. Thus, (m+1) more equations are required

to solve the problem.

Observing the structure of Fig. 2, it is found that

only the first row exists if α = 0 and β = 0.

Therefore, we can determine a set of particular

solutions, π(0, j), j = 1, 2, …, m, as follows.

.,,2,1),0,0(),0( mj

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

(7)

The final equation is provided by the

normalization condition:

.1),(

∑∑

−

(8)

Equations (5), (6), (7), and (8) are sufficient to

evaluate the state probabilities π(i, j), 0 ≤ i ≤ m, 0 ≤ j

≤ m - i.

4 PERFORMANCE METRICS

4.1 The Probability That All Channels

Are Not Available

The probability that all channels are not available

(either in service or in failure), denoted by P

, is the

sum of the state probabilities with i + j = m, 0 ≤ i ≤

m. This event is seen by an external observer.

.),(

∑

−=

imiP

(9)

4.2 The Probability That an Arriving

Call Sees All Channels Not

Available

The probability that an arriving call sees all channels

not available (either in service or in failure), denoted

by P

, is the probability that the initiating SS finds

all channels not available when placing a call

request. This metric is similar to P

except that the

observer is an internal source. Note that the

proposed model is a finite source system, the

PASTA property does not hold. By using the arrival

theorem (Kobayashi and Mark, 2009), the P

obtained by replacing N with N -1 in (9).

,),(

]1[

∑

−

−=

Nin

imiP

(10)

where

),(

]1[

N −

means the steady state probability

at (i, j) when the total number of SSs in the network

is N-1. Following this notation, the equation (9) can

be re-written as

.),(

][

∑

−=

Nex

imiP

4.3 The Mean System Throughput

The mean system throughput, denoted by T

sys

, is

defined as the mean number of calls being served

per unit time. Thus, we have

.),(

][

∑∑

−

sys

jijT

πμ

(11)

4.4 The Mean Number of Channels in

Failure

The mean number of channels in failure, denoted by

, is defined as the mean number of failed channels

in steady state. Thus, we have

MODELING AND ANALYSIS OF A POWER LINE COMMUNICATION NETWORK SUBJECT TO CHANNEL

FAILURE

187

.),(

][

∑∑

−

jiiN

(12)

4.5 The Mean Number of Calls Being

Served

The mean number of calls being served, denoted by

, is defined as the mean number of calls in service

in steady state. Thus, we have

.),(

][

∑∑

−

jijN

(13)

5 NUMERICAL RESULTS

In this section, we present the numerical results in

the following configuration: N = 40 or 60, m = 10.

The arrival rate λ changes from 1 to 8. The other

parameters μ, α, and β are set separately with

variable values in each figure. Note that all

parameters are given in dimensionless units, which

can be mapped to specific units of measurement.

To validate our analysis, we also developed a

discrete-event simulator for the proposed model. The

simulation was implemented in MATLAB. For

convenient illustration, we only show one group of

simulation results as a comparison. In the illustrated

figures, an excellent match between the analysis and

simulation can be observed. Each simulated data

point was averaged over 5,000 trials and the

associated 95% confidence intervals were computed.

Fig. 3 shows how the probability P

changes

with respect to various parameters. We observe that

increases with the increase of call arrival rate λ

or the service time 1/μ. As λ increases, the system is

easier to get full channel occupancy. As the service

time increases, the system becomes more difficult to

release a channel. In our parameter configuration,

we also observe that P

displays different trends

with respect to α and β. The increase of the channel

failure rate or the required recovery time delays the

channel availability to the initiating call requests.

In Fig. 3, we also observe that P

increases with

the increase of the network population N. When N

increases, the total call arrivals to the system per unit

time will increase and the system will be easier to

get full channel occupancy. The performance of P

is similar to that of P

. Due to space limitation, we

omit the figures here.

Fig. 4 shows how the mean system throughput

sys

changes with respect to various parameters. We

observe that T

sys

increases with the increase of λ, μ,

or N. As λ, μ, or N increases, the mean number of

Figure 3: The probability that all channels are not

available.

Figure 4: The mean system throughput.

calls entering the system or the mean number of

calls processed per unit time will be increased. We

also observe that T

sys

decreases with the increase of

channel failure rate or the required recovery time. A

more frequent channel failure event or a longer

required recovery time will negatively affect the

performance of the system throughput.

Fig. 5 shows how the mean number of failed

channels N

changes with various parameters. We

observe that N

increases with the increase of λ or N,

and decreases with the increase of μ. As λ or N

increases, more calls occupy the channels per unit

time, leading to more channels subject to failure.

Note that in our model, it is assumed that the

channels are subject to failure during service. We do

not consider the failure events for idle channels due

to no calls being served (although there is a little

impact to an initiating call that happens to access an

idle channel being in failure). As μ increases, a call

completes its service in shorter duration, reducing

the chance for a call to encounter a channel failure

event. We also observe that N

increases with the

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

188

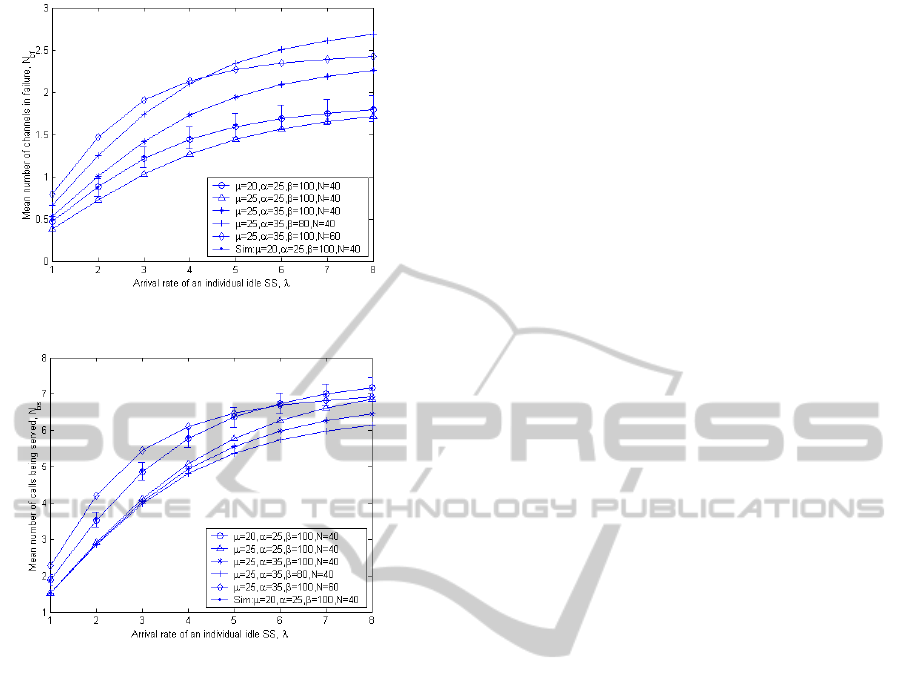
Figure 5: The mean number of channels in failure.

Figure 6: The mean number of calls being served.

increase of channel failure rate or the required

recovery time. The reason is obvious.

Fig. 6 shows how the mean number of calls being

served N

changes with various parameters. We

observe that N

increases with the increase of λ or

N, and decreases with the increase of μ. This agrees

with our intuition. As λ or N increases, a snapshot in

steady state will capture more calls being served. On

the other hand, the larger μ means the faster

processing rate, leading to less calls in service

captured by a snapshot. We also observe that N

decreases with the increase of channel failure rate α

or the required recovery time 1/β. As α is increased

or β is decreased, a snapshot in steady state will

capture less calls being served.

6 CONCLUSIONS

We analytically modeled a PLC network with finite

population and evaluate its performance at the call-

level through a queuing theoretic framework. The

call subject to channel failure holds at the channel

until the channel is recovered. The channels

obtained from an OFDM based transmission

technique are subject to failure during service due to

noise/disturbance. We determined the steady-state

solution of the proposed model and derived several

performance metrics of interest. Numerical and

simulation results are presented to show the impact

of system parameters on the performance metrics.

The proposed modeling method and the derived

metrics can be used for evaluation and design of

future PLC networks.

REFERENCES

Stantcheva, M., Begain, K., Hrasnica, H., Lehnert, R.,

2000. Suitable MAC protocols for an OFDM based

PLC network. 4

Int’l Symposium on Power-Line

Communications and its Applications.

Zimmerman, M., Dostert, K., 2002. Analysis and

modeling of impulsive noise in broad-band powerline

communications. IEEE Trans. on Electromagnetic

Compatibility, vol. 44, pp. 249–258.

Hrasnica, H., Haidine, A., 2000. Modeling MAC layer for

powerline communications networks. 4th Int’l

Symposium on Power-Line Communications and its

Applications.

Katayama, K., Yamazato, T., Okada, H., 2006. A

mathematical model of noise in narrowband power

line communication systems. IEEE J. Selected Areas

in Comm., vol. 24, pp. 1267–1276.

Haring, J., Vinck, H., 2000. OFDM transmission corrupted

by impulsive noise. 4th Int’l Symposium on Power-

Line Communications and its Applications.

Amirshahi, P., Navidpour, S., Kavehrad, M., 2006.

Performance analysis of OFDM broadband

communications system over low voltage powerline

with impulsive noise. IEEE ICC’06, pp. 367–372.

Yu, J., Yu, H., Lee, Y.-H., 2003. Design of a power-line

modem for monitoring and control systems. 7th Int’l

Symposium on Power-Line Communications and its

Applications.

Kobayashi, H., Mark, B.L., 2009. System modeling and

analysis: foundations of system performance

evaluation. Upper Saddle River, NJ: Pearson.

MODELING AND ANALYSIS OF A POWER LINE COMMUNICATION NETWORK SUBJECT TO CHANNEL

FAILURE

189