COMPARISON OF SURFACE DATA

Exploring Real Samples Similarity for the Modelling of Engraving

Jana Hájková and Jakub Kotásek

Department of Computer Science and Engineering, University of West Bohemia, Univerzitní 8, Pilsen, Czech Republic

Keywords: Ablation, Laser engraving, Comparison, Real data, Confocal microscope, Similarity, MSE, PSNR.

Abstract: The paper deals with the topic of real samples comparison. The whole research is processed as a part of the

laser engraving modelling and simulation, for which real engraved and scanned samples are used as the

input and which are further processed before their usage. All samples are represented as height maps, so we

try to use MSE or PSNR computation for the comparison of samples. However, because of a special

character of the samples, several problems have to be solved. Finally, the results for the whole set of data

engraved into steel surface is presented and some interesting results are shown.

1 INTRODUCTION

This work is a part of larger project dealing with

development of a special laser device with precise

control and its modelling and simulation, which

should assure exact results usable for physical

research. All methods and results described in this

paper solve only a small but very important part of

the whole research of data pre-processing, more

concretely, the mutual comparison of processed real

samples.

Methods for sample comparison can be used for

example for the verification of the modelling and

simulation or, as shown in this paper, for exploring

real data. Real data comparison is important for

discovering the similarities among real samples and

the interaction between the laser beam and the

material surface. Because all the used methods are

already described in detail in (Hájková, 2008), only

some basics are outlined in Section 4, the main aim

of the paper is to show similarities and divergences

of real samples in dependence on the engraved

experiment (described in Section 5).

2 LASER ABLATION

Because we want to explore real samples and

compare them, we should first understand the

process of laser engraving and especially the

material ablation in detail. A laser beam is an

electromagnetic radiation. When this radiation

strikes a surface of a material, some radiation is

reflected, some absorbed and some transmitted. The

irradiated material is most affected by the absorbed

part of the radiation, which causes heating of the

surface. The heat generated in the surface directly

affected by the laser beam is conducted into the

material. If the laser intensity is high enough, the

material heats, melts, and if it reaches the boiling

point, it starts to vaporize. A part of vaporized

particles interacts with the laser beam and creates

plasma, the other particles, which are not affected by

the laser beam, approximately 18% of them as

mentioned in (Anisimov, 1968), condense back to

the surface of the material.

The previous description relates to the situation

when the laser irradiates the sample continuously

and the material is heated constantly during the

whole engraving. If we engrave more laser beam

pulses into one place on the surface, the temperature

of the material increases during each laser pulse.

Between each two consecutive pulses, the material

surface cools down in part, but not fully. That is why

the initial temperature is always higher and higher

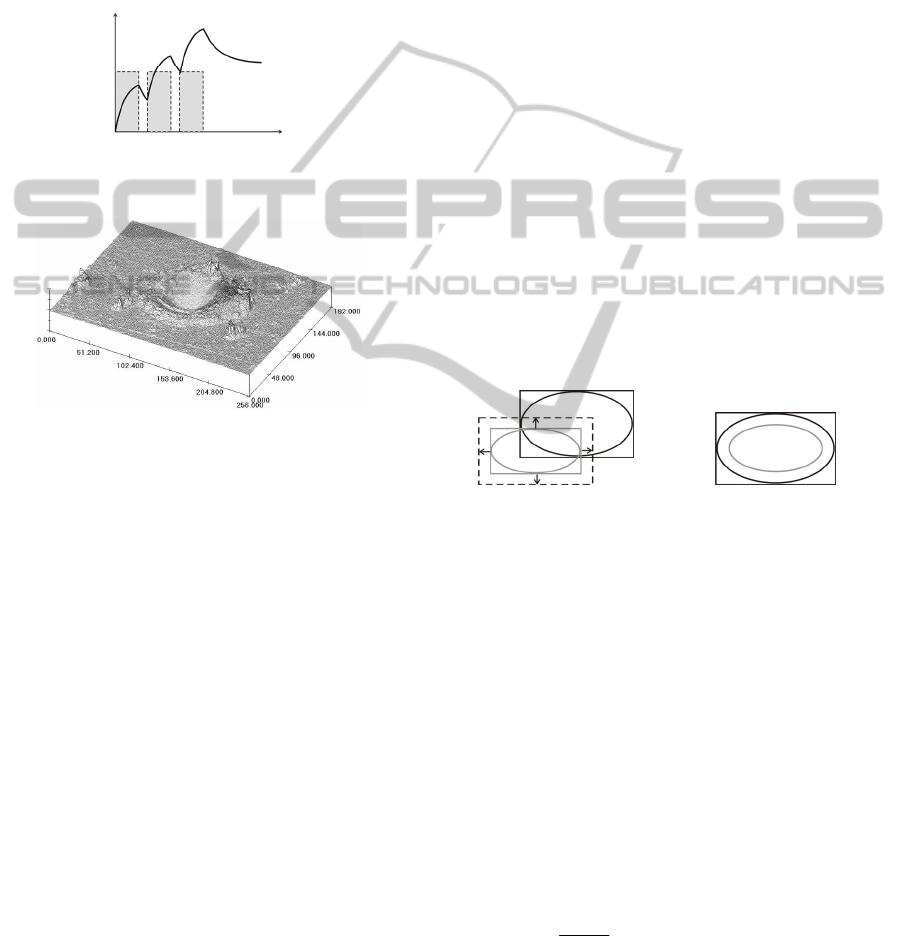
with each subsequent pulse. The evolution of

temperature of such sample is shown in Figure 1.

To sum up the whole engraving process: if the

surface of the material is exposed to an intense

pulsed laser beam it creates a rapid rise in local

temperature. The surface warms up and the material

starts to ablate. The ablated material then redeposites

around the irradiated area and together with various

273

Hájková J. and Kotásek J..

COMPARISON OF SURFACE DATA - Exploring Real Samples Similarity for the Modelling of Engraving.

DOI: 10.5220/0003485802730276

In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 273-276

ISBN: 978-989-8425-77-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

local defects and original roughness of the material

causes many problems in samples processing.

Finally, at the exposure site, a pit with a transition

ring around it is left behind (an example can be seen

in Figure 2). The result of the engraving process

depends on the used material, its roughness, and

parameters of the laser. The whole process is

described in detail in (Dahotre and Harimkar, 2008)

or (Steen, 1991).

Figure 1: Evolution of surface temperature during

engraving multiple laser beam pulses into the same point.

Figure 2: Sample 3D view from the conf. microscope.

3 REAL DATA DESCRIPTION

As already mentioned, we use real data as the input

for the modelling of laser engraving. Samples

originate from real samples engraved by a laser into

a material surface. All samples are engraved into the

specified material (we use steel) with the given laser

(BLS-100 Nd:YAG solid-material, lamp-pumped

laser with the wavelength of 1064nm), each sample

is separately measured by a confocal microscope

(Olympus LEXT OLS3100) and saved in the form

of a height map. This height map is formed by a

matrix of real numbers, which express the heights in

a uniform rectangular grid. The dimensions of the

samples reach approximately several hundreds of

micrometers.

3.1 Experiment Description

We use the special testing data set consisting of

samples engraved by the laser into a single point of

the material. Such testing data should prevent

potential faults caused by the external influences in a

maximum possible way. The number of pulses goes

in sequence: 1, 2, 5, 10, 20, 30, ..., 100. Because

each sample is unique, samples differ from each

others even if the same experiment description has

been engraved repeatedly under the same conditions

and with the same laser settings. That is why each

experiment is repeated five times in order to get

sufficiently representative data set.

4 METHODS FOR COMPARISON

If we compare two height maps, we should make

sure that both the surfaces are aligned properly. That

is why it is very important to regularize all the

samples before the comparison itself. Moreover, we

need to compare only those areas which were

modified by the laser beam. For this purpose, we use

methods designed for the automatic detection of the

heat-affected area described, e.g. in (Hájková, 2011).

As can be seen in Figure 3a, the size of both

areas can differ and so we have to unify (enlarge)

the detected areas so that they both have the same

dimension and the heat-affected areas lie exactly in

the middle (as shown in Figure 3b).

a) b)

Figure 3: a) Two heat-affected areas of different sizes;

b) unifying expansion of selection dimensions.

Finally, the level of material in both the samples

is recomputed to have the same height. Then, we can

compute the similarity of both samples. For our test,

we have used two approaches: MSE and PSNR

computation described in following sections.

4.1 MSE (Mean Square Error)

This method computes the mean square error (MSE)

of two height maps. It is defined by the equation 1,

where W×H represent the dimensions of the height

maps and A(i, j) and B(i, j) indicate single points in

the given position [i,j] in the height map grid. The

resulting value expresses the average error for each

point.

() ()()

∑∑

−

jiBjiA

MSE

(1)

It is not difficult to see that the more identical the

samples are, the lower the MSE is computed. So, if

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

274

we want to find a pair of height maps that are the

most similar, we look for the minimal value of MSE.

4.2 PSNR (Peak Signal-to-Noise Ratio)

The PSNR method uses MSE as a semi result. The

PSNR value is computed according to the equation

2, where the MAX value represents the highest point

in the height map.

⎟

⎠

⎞

⎜

⎝

⎛

MSE

MAX

PSNR

log.10

(2)

PSNR works in an inverse way, so if we are

looking for the most similar height maps, their

PSNR has to be the highest one.

5 RESULTS

We have used the approaches and methods described

above to explore a real data set to discover the

similarities and differences of samples. For our

testing, we have used an experiment described in

Section 3.1 that is a sequence of 1 to 100 laser beam

pulses engraved into a single point on a steel

surface. This sequence was engraved five times,

scanned and the heat-affected area was detected for

each sample.

In the next step, all samples were mutually

compared (each with each other) and the results of

MSE and PSNR were collected in (Kotásek, 2010).

Then we have selected different combinations of

comparisons and we were searching for variations

within them. Although there were some small

differences, the global trend was the same for all of

them and is discussed as follows. All values are

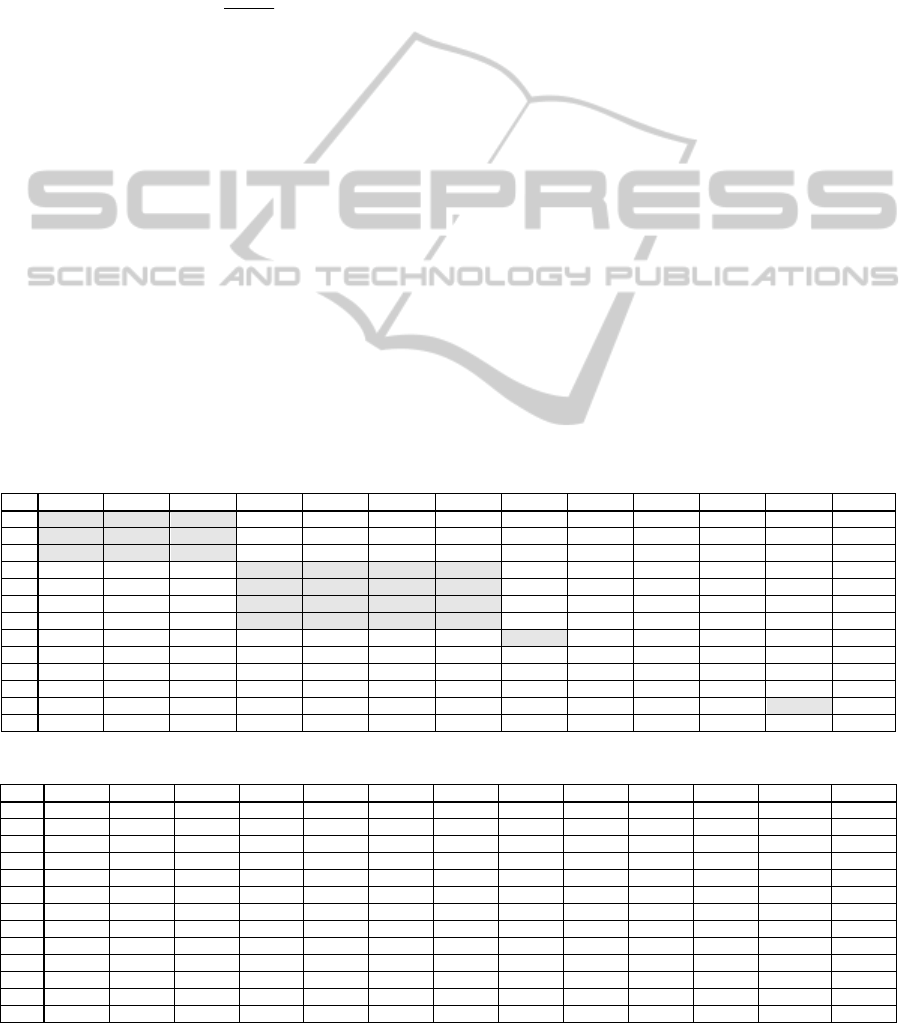
summarized in Table 1 (MSE) and Table 2 (PSNR).

5.1 Measured Values

Let us have a look on Table 1 first, where MSE

values are summarized. The more similar both tested

samples are, the smaller the MSE is computed. That

is why the smallest values are expected on the

diagonal of the table, where samples with the same

number of laser beam pulses are compared. In each

column of the table, the smallest value is highlighted

in bold. Although in some cases the minimal value

does not lie exactly on the diagonal, it is always very

close, most usually the neighbouring one. These

imperfections are typically caused by the local

defects that can be found in the samples. In Table 2

with PSNR results, the highest values are computed

for the most similar samples and are also highlighted

in bold. Also in this case similar problems with the

position of the maximal values can be found.

Besides exploring the real samples discussed in

Table 1: Results of the MSE computation.

1 2 5 10 20 30 40 50 60 70 80 90 100

00 1

55 11

89 12

51 10

90 9

66 27

27 29

13 41

58 44

87 23

80 44

2 2,00

1,35

3,26 10,81 11,55 10,37 8,98 24,55 26,41 37,52 40,83 21,41 40,33

5 1,55 3,26

0,81

10,73 11,59 9,91 9,70 27,24 29,40 42,41 45,73 24,91 45,27

10 11,89 10,81 10,73

1,16 2,10 2,50

2,34 7,04 9,41 16,04 18,69 8,04 17,67

20 12,51 11,55 11,59 2,10 2,37 3,01 2,56 7,27 9,53 16,43 18,82 8,37 18,40

30 10,90 10,37 9,91 2,50 3,01 2,83 2,75 8,65 10,80 18,30 20,68 9,19 20,34

40 9,66 8,98 9,70 2,34 2,34 2,75

1,15

6,99 8,78 16,00 18,22 6,70 19,15

50 27,27 24,55 27,24 7,04 7,27 8,65 6,99

2,40 4,23

6,23 8,04 3,79 7,70

60 29,13 26,41 29,40 9,41 9,53 10,80 8,78 4,23 5,07 7,06 8,69 4,33 8,73

70 41,58 37,52 42,41 16,04 16,43 18,30 16,00 6,23 7,06

5,04 6,85

6,12 6,23

80 44,87 40,83 45,73 18,69 18,82 20,68 18,22 8,04 8,69 6,85 7,19 7,67 7,85

90 23,80 21,41 24,91 8,04 8,37 9,19 6,70 3,79 4,33 6,12 7,67

1,03

7,72

100 44,38 40,33 45,27 17,67 18,40 20,34 19,15 7,70 8,73 6,23 7,85 7,72

3,45

Table 2: Results of the PSNR computation.

1 2 5 10 20 30 40 50 60 70 80 90 100

25 36

62 25

85 23

75 26

39 25

55 22

05 21

40 20

87 19

33 20

88 18

2 35,25

37,91

31,37 26,60 24,2 26,55 26,05 23,01 22,20 21,83 20,18 21,83 19,53

5 36,62 31,37

41,25

26,66 24,42 27,09 25,27 21,93 21,30 20,60 19,04 20,37 18,43

10 25,85 26,60 26,66

44,97 41,76 41,01

40,03 34,14 31,27 29,78 27,35 30,49 26,92

20 23,75 24,20 24,42 41,76 38,59 39,96 38,64 34,46 31,64 29,90 27,46 30,21 26,92

30 26,39 26,55 27,09 41,01 39,96 40,07 39,75 32,53 30,45 28,74 26,71 29,76 25,95

40 25,55 26,05 25,27 40,03 38,64 39,75

43,19

34,37 31,97 30,04 28,22 32,10s 26,18

50 22,05 23,01 21,93 34,14 34,46 32,53 34,37

42,51 40,61

39,07 35,60 39,62 34,78

60 21,40 22,20 21,30 31,27 31,64 30,45 31,97 40,61 39,18 39,55 36,54 38,88 34,51

70 20,87 21,83 20,60 29,78 29,90 28,74 30,04 39,07 39,55

40,86 39,21

40,20 38,25

80 19,33 20,18 19,04 27,35 27,46 26,71 28,22 35,60 36,54 39,21 37,09 36,86 35,93

90 20,88 21,83 20,37 30,49 30,21 29,76 32,10 39,62 38,88 40,20 36,86

47,32

34,44

100 18,66 19,53 18,43 26,92 26,92 25,95 26,18 34,78 34,51 38,25 35,93 34,44

40,71

COMPARISON OF SURFACE DATA - Exploring Real Samples Similarity for the Modelling of Engraving

275

this paper, we also wanted to discover, which

computational method is better to use for the

automatic determining of the most similar samples.

It is noticeable that the MSE and the PSNR give

analogous results for determining the similarity

(extremes in both tables are bold at the same

positions), but the MSE seems to give better results

for the automatic comparison, because the values

representing the most similar samples can be well

distinguished from the others (e.g. by thresholding).

The most similar samples are in Table 1 highlighted

with gray colour.

5.2 Results Visualization Discussion

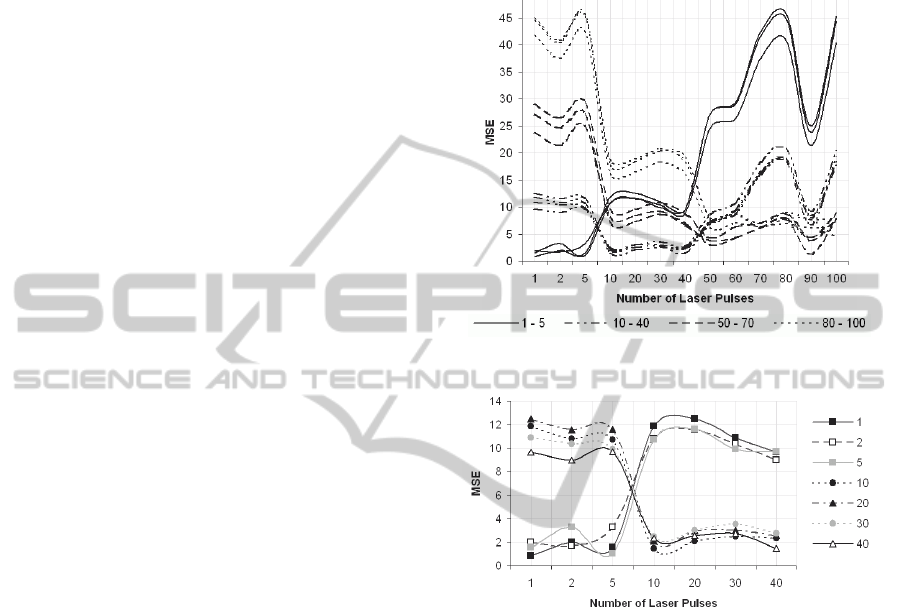
Visualization of Table 1 brings some more

interesting facts. The MSE results can be seen in

Figure 4. In the plot, the horizontal axis shows the

sequence of samples and the curves express the

similarity of the individual samples. The distance

between the samples determined as similar and not-

similar is noticeable. An interesting characteristic

can be seen in the plot the cumulating of the curves

representing the similarity of a sample to each other.

If we take a look more closely, we can see that

curves representing the samples with small number

of pulses (1, 2 and 5) are placed close to each other

in the plot. Also, the values in Table 1 do not differ a

lot. The same situation can be discovered for

samples with 10 to 40 pulses and then for samples

with 50 to 100 pulses. So, samples can be divided

into groups, in which they are similar to each other,

but are very different from samples in the other

groups. This is also the reason, why the curves are

not labelled separately, but only in sets. The

situation between two groups is more closely shown

in Figure 5.

6 CONCLUSIONS

As can be seen from the described results and plots,

the number of laser pulses engraved into one point

of the material influences the ablation process a lot.

What is the reason of the described relations?

Accumulating temperature during the ablation

process and so changing nature of the irradiated

material. The heated material behaves differently if

it is heated for a while or for a longer time.

So far, we have studied mainly samples engraved

into steel, where all the laser pulses were engraved

into a single point on the material surface. Our

further plan is to explore the results when the laser is

moving above the material surface with a constant or

even a variable speed. In our future work, we would

also like to conduct more experiments with different

laser settings and/or engraved into different

materials and search for the next dependencies, how

the engraved experiments influence the ablation

process and the final shape of the material surface.

Figure 4: MSE results visualization.

Figure 5: MSE computation results – detail of sweeping

change of samples similarity.

REFERENCES

Anisimov, S. I., 1968: Vaporization of metal absorbing

laser radiation. Soviet Physics JETP, Vol. 27, pp. 182.

Dahotre, N. B., Harimkar, S. P., 2008: Laser Fabrication

and Machining of Materials, Springer, New York,

USA.

Hájková, J., 2008: Approaches for Automatic Comparison

of Laser Burned Samples, Proceedings of the 9

International PhD Workshop on Systems and Control.

Izola, Slovenia.

Hájková, J., 2011: Laser Engraving Modelling: Compari-

son of Methods for the Heat-Affected Area Detection,

Proceedings of the 10

International Conference

APLIMAT 2011. STU Bratislava, Slovakia.

Kotásek, J.: Metody porovnávání výškových map (Methods

for Height Maps Comparison), Bachelor Thesis,

University of West Bohemia, 2010.

Steen, W. M., 1991: Laser Material Processing.

Springer-Verlag, New York Berlin Heidelberg.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

276