
FINANCIAL TIME SERIES FORECAST USING SIMULATED
ANNEALING AND THRESHOLD ACCEPTANCE GENETIC
BPA NEURAL NETWORK
Anupam Tarsauliya, Ritu Tiwari and Anupam Shukla
Soft Computing and Expert System Laboratory, ABV-IIITM, Gwalior, 474010, India
Keywords: Simulated annealing, Threshold acceptance, Genetic, ANN, Time series, Financial forecast.
Abstract: Financial time series forecast has been eyed as key standard job because of its high non-linearity and high
volatility in data. Various statistical methods, machine learning and optimization algorithms has been
widely used for forecasting time series of various fields. To overcome the problem of solution trapping in
local minima, here in this paper, we propose novel approach of financial time series forecasting using
simulated annealing and threshold acceptance genetic back propagation network to obtain the global minima
and better accuracy. Time series dataset is normalized and bifurcated into training and test datasets, which is
used as supervised learning in BPA artificial neural network and optimized with genetic algorithm. Results
thus obtained are used as seed for start point of simulated annealing and threshold acceptance. Empirical
results obtained from proposed approach confirm the outperformance of forecast results than conventional
BPA artificial neural networks.
1 INTRODUCTION
Forecasting is generally referred as the process of
making statements about events whose actual
outcomes have not yet been observed. Forecasting
has got various applications in many situations such
as weather forecasting, financial forecasting, flood
forecasting, technology forecasting etc. Of these
financial forecasting has been challenging problem
due to its non-linearity and high volatility (Yixin and
Zhang, 2010). Forecasting assumes that some
aspects of past patterns will continue in future. Past
relationship of it can be discovered through study
and observation of data. Main idea behind
forecasting has been to devise a system that could
map a set of inputs to set of desired outputs (Marzi,
Turnbull and Marzi, 2008). ANNs have widely been
used for the forecasting purpose because of their
ability to learn non-linear and complex data (Eng et
al., 2008). ANNs is trained such as a set of inputs
maps a set of desired output. These networks can
hence automatically assume any shape that carries
forward the task of determination of the outputs to
the presented input. Any problem has predefined
inputs and outputs. The relation between the inputs
and the outputs is done by a set of rules, formulae or
known patterns. These networks do the task of
predicting these rules such that the overall system
performs better when any of the data from the
historical database is again presented.
The ANNs by their basic architecture represent
the human brain (Kumar et al., 2008). They consist
of a set of artificial neurons. The various artificial
neurons are joined or connected to each other by
connections. These connections aid the flow of
information or data between the neurons. Artificial
neurons behave similar in concept to their biological
counterparts. The task of any fundamental artificial
neuron may be divided into two parts. The first part
does the weighted addition of the inputs presented to
it. Here each connection has a weight associated
with it. As the input arrives through the connection,
it is multiplied by the corresponding weight. The
addition of all such inputs is performed. The second
part of the neuron consists of an activation function.
The weighted addition of the first part is passed
through the activation function. This is the final
output of the system (Zhao et al., 2010). The
activation function is usually non-linear to enable
the ANNs solve nonlinear problems.
GAs can be used to optimize various parameters
and to solve many problems in real time; these
solutions may otherwise not be possible in finite
time. GA’s are also used for various search-related
172
Tarsauliya A., Tiwari R. and Shukla A..
FINANCIAL TIME SERIES FORECAST USING SIMULATED ANNEALING AND THRESHOLD ACCEPTANCE GENETIC BPA NEURAL NETWORK.
DOI: 10.5220/0003492101720177
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 172-177
ISBN: 978-989-8425-54-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
operations (Etemadi et al., 2009). Genetic algorithm
is used for further optimization of the neural
network. These algorithms model complex problems
and return the optimal solution in an iterative
manner. Genetic Algorithm as a solution for
optimization problems based on natural selection
keeps an initial population of solution candidates
and evaluates the quality of each solution candidate
according to a specific cost function. GA repeatedly
modifies the population of individual solutions. At
each step, the genetic algorithm selects individuals
at random from the current population to be parents
and uses them produce the children for the next
generation. Over successive generations, the
population evolves toward an optimal solution
(Yang and Zhu, 2010).
Simulated Annealing is a Monte Carlo technique
that can be used for seeking out the global
minimum. The effectiveness of SA is attributed to
the nature that it can explore the design space by
means of neighbourhood structure and escape from
local minima by probabilistically allowing uphill
moves (Khosravi et al., 2010). Compared with
traditional mathematical optimization techniques,
SA offers a number of advantages: first, it is not
derivative based, which means that it can be used for
optimization of any cost function, regardless of its
complexity or dimensionality, and secondly, it can
explore and exploit the parameter space without
being trapped in local minima (Suman and Kumar,
2006). Threshold acceptance uses a similar approach
alike simulated annealing, but instead of accepting
new points that raise the objective with a certain
probability, it accepts all new points below a fixed
threshold (Pepper, Golden and Wasil, 2002).
2 ALGORITHMS AND METHODS
2.1 Artificial Neural Network
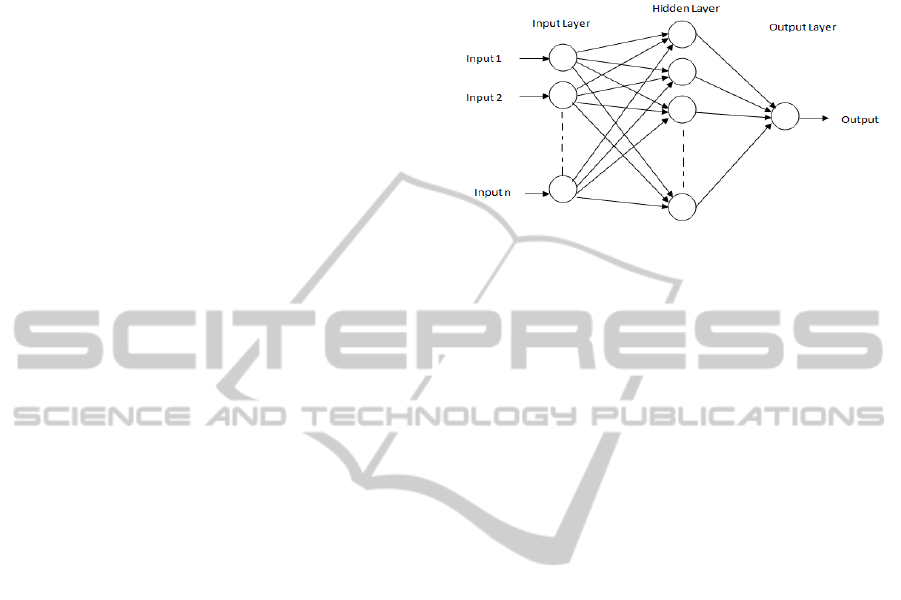
The General BPA Neural Network architecture as
shown in Fig. 1 includes input layer, hidden layer
and output layer. Each neuron in input layers are
interconnected with neurons in hidden layers with
appropriate weights assigned to them (Shukla,
Tiwari and Kala, 2010). Similarly each neuron of
hidden layer in interconnected with output layer
neuron with weights assigned to the connection. On
providing learning data to the network, the learning
values are passed through input to hidden and finally
to output layer where response for input data is
obtained. For optimizing the error obtained, the error
values are back propagated to make changes in
weights of input to hidden layer and hidden to output
layer. With error back propagation input response
are made converged to desired response.
Figure 1: General Architecture of an ANN.
BPA uses supervised learning in which trainer
submits the input-output exemplary patterns and the
learner has to adjust the parameters of the system
autonomously, so that it can yield the correct output
pattern when excited with one of the given input
patterns (Lee, 2008).
2.2 Genetic Algorithm
Genetic algorithms (GA) function by optimizing an
objective function. They exploit the structure of the
error surface. GAs does not assume that the error
surface is unimodal, or even that its derivative exists
(Shopova et al., 2006). Such assumptions are
required for efficient use of traditional optimization
strategies. Since many practical design problems
involve nonlinear and multimodal problem spaces,
the GA approach is attractive.
Genetic Algorithm evolves ANNs by fixing the
values and the weights and biases of the various
nodes i.e. the GA optimizes the network parameters
for better performance. Steps followed for evolution
of ANN are problem encoding, creation of random
initial state, fitness evaluation, and genetic operator
including selection, crossover, mutation and elite,
generate next generation, testing and verification
(Altunkaynak, 2009) as shown in Fig. 2.
The fitness function is derived from two
categories of errors: (1) the error of pattern k, which
is the difference between the actual and the forecast
values at any current pattern k, and (2) the total error
of all patterns.
Fitness = error [k] +error [total]
FINANCIAL TIME SERIES FORECAST USING SIMULATED ANNEALING AND THRESHOLD ACCEPTANCE
GENETIC BPA NEURAL NETWORK
173

Figure 2: Flow Chart for working of Genetic Algorithm.
Once the GA reaches its optimal state and terminates
as per the stopping criterion, we get the final values
of the weights and biases. We then create the ANN
with these weights and bias values; which is then
regarded as the most optimal ANN to result from the
ANN training. We can then use the evolved ANN
for testing.
2.3 Simulated Annealing & Threshold
Acceptance
Simulated annealing (Kirkpatrick, Gelatt and
Vecchi, 1983) is a method for solving unconstrained
and bound-constrained optimization problems. The
method models the physical process of heating a
material and then slowly lowering the temperature to
decrease defects, thus minimizing the system
energy.
At each iteration of the simulated annealing
algorithm (Zain, Haron and Sharif, 2011), a new
point is randomly generated. The distance of the new
point from the current point, or the extent of the
search, is based on a probability distribution with a
scale proportional to the temperature. The algorithm
accepts all new points that lower the objective, but
also, with a certain probability, points that raise the
objective. By accepting points that raise the
objective, the algorithm avoids being trapped in
local minima, and is able to explore globally for
more possible solutions. The annealing schedule is
the rate by which the temperature is decreased as the
algorithm proceeds. The slower the rate of decrease,
the better the chances are of finding an optimal
solution, but the longer the run time (Liu and Zhu,
2010). An annealing schedule is selected to
systematically decrease the temperature as the
algorithm proceeds. As the temperature decreases,
the algorithm reduces the extent of its search to
converge to a minimum.
Threshold acceptance uses a similar approach
alike simulated annealing, but instead of accepting
new points that raise the objective with a certain
probability, it accepts all new points below a fixed
threshold (Pepper, Golden and Wasil, 2002). The
threshold is then systematically lowered, just as the
temperature is lowered in an annealing schedule.
Because threshold acceptance avoids the
probabilistic acceptance calculations of simulated
annealing, it may locate an optimizer faster than
simulated annealing (Lidia and Carr, 1985).
The following is an outline of the steps
performed (Liu and Zhu, 2010) for both the
simulated annealing and threshold acceptance
algorithms as shown in Fig. 3:
Figure 3: Flow Chart for working of Simulated Annealing
and Threshold Acceptance.
3 EXPERIMENT AND RESULTS
3.1 Research Data
We have used two different data sets for our
research. The data (un-normalized) have been
collected from Prof. Rob J Hyndman’s website
http://robjhyndman.com/TSDL/ . Data sets analyzed
are as:
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
174
Daily closing price of IBM stock, Jan. 01 1980 -
Oct. 08 1992. Daily S & P 500 index of stocks, Jan.
01 1980 - Oct. 08 1992. (Hipel and McLeod, 1994)
Table 1: Time Series Data Sets Description.
Time
Series
Standard
Deviation
Mean Count
Daily IBM 28.76493 105.6183 3333
Daily S&P 97.01113 236.1225 3333
3.2 Methodology
We adopted and performed the following steps for
training and testing the data series as shown in Fig.
4. The brief description of each step is as follows:
Figure 4: Flow Chart for Adopted Methodology.
We first load the given time series data set,
which is divided into training and testing dataset. A
random dataset division is followed to result 70% of
dataset as training dataset and remaining 30% as
testing dataset. Training dataset outcome of random
data set division followed is used for defining and
building the architecture of artificial neural network.
Training dataset is used for learning of the neural
network using supervising learning. Testing dataset
is used for validation and testing of the learned
neural network. Simulated output of the neural
network for testing dataset is compared against the
target output. Thus it is used in formulating accuracy
of the neural network.
After the network defined is optimized using
genetic algorithm. Process of genetic algorithm as
described before is followed. First an initial random
population is generated. Various genetic operation
selection, crossover and mutation are followed.
Population is then evaluated using fitness function.
If stopping criteria is met or goal is met, the
algorithm is stopped else next generation process is
followed.
Thus obtained optimized artificial neural
network is further optimized using Simulated
Annealing/ Threshold Acceptance algorithm.
Optimized parameters value obtained from genetic
optimization is used as start initial point for the
algorithms. Process as described in section 2.3 is
followed. Optimized parameter values after
simulated annealing/ threshold acceptance is used
for formulating final artificial neural network. This
neural network is thus used for final simulation of
results and formulating the accuracy of the system.
3.3 Empirical Results
ANN Parameters used:
Neurons (Input, Hidden, Output) = (10, 05, 01)
Learning Rate: 0.3
Momentum: 0.7
Table 2: Mean RMSE for different algorithms and data.
Algorithm Used
Mean RMSE
Daily IBM
Mean RMSE
Daily S&P
BPA 3.7106 6.0846
Simulated
Annealing
Genetic BPA
2.5426 5.4519
Threshold
Acceptance
Genetic BPA
2.5321 5.6382
It can be seen from the table 2 that estimation are
better for simulated annealing and threshold
acceptance algorithms approach than BPA
algorithm. It can also be drawn that from above
results that performance of simulated annealing and
threshold acceptance is financial time series specific,
as simulated annealing estimates better for Daily
S&P while threshold acceptance for Daily IBM.
3.4 Graphical Analysis
Below described graphs are drawn for actual vs.
Predicted values with Index Value on Y-Axis and
Days on X-Axis.
FINANCIAL TIME SERIES FORECAST USING SIMULATED ANNEALING AND THRESHOLD ACCEPTANCE
GENETIC BPA NEURAL NETWORK
175
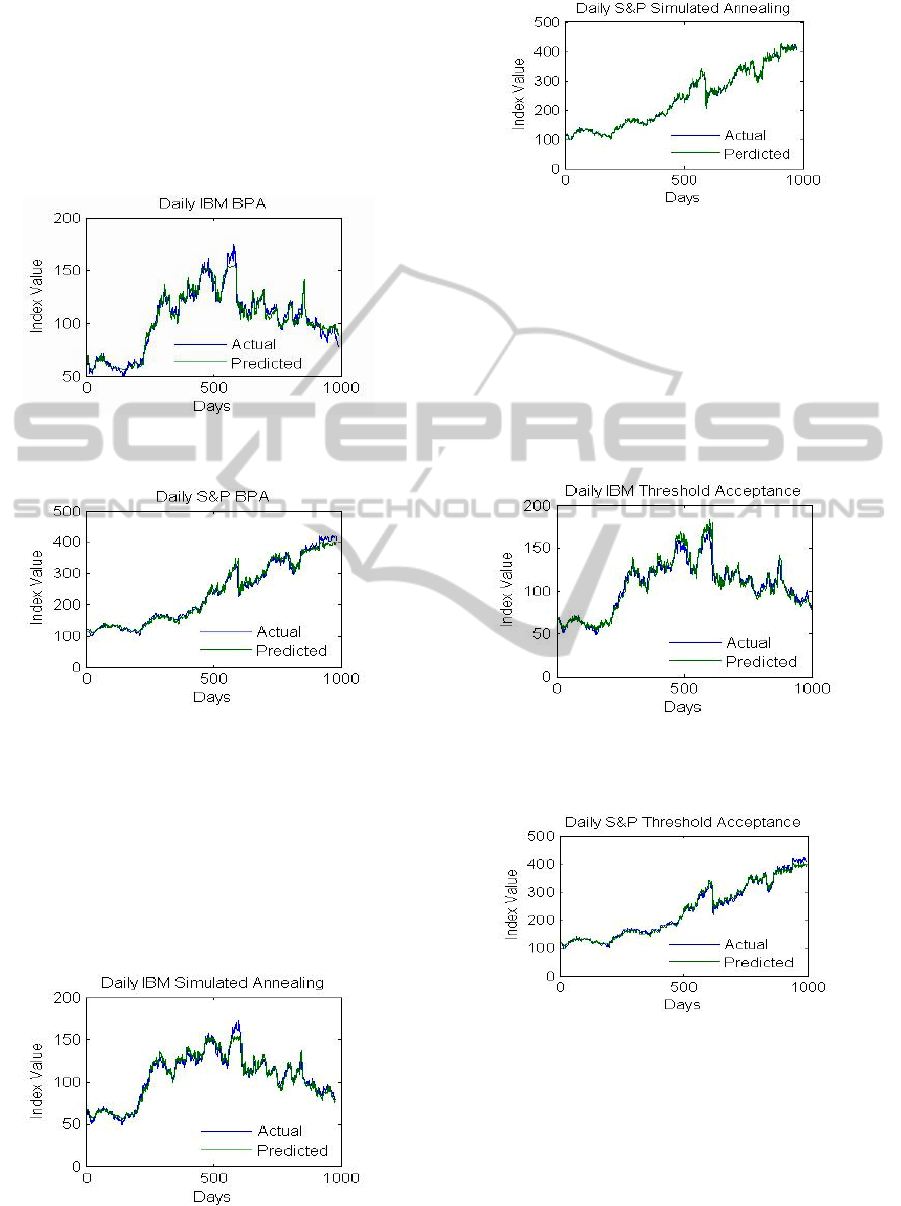
Fig. 5 and Fig. 6 shown below are comparison
graph plotted between desired output and simulated
output using conventional BPA for dataset of Daily
IBM and Daily S&P respectively. It is observed that
trends are well learned by network but volatilities
in data are not well predicted with some vertical and
horizontal lags present. It can also be observed that
network lacks generalization ability.
Figure 5: Graph for Daily IBM using traditional BPA
Algorithm. Daily IBM Mean RMSE = 3.7106.
Figure 6: Graph for Daily S&P using traditional BPA
Algorithm. Daily S&P Mean RMSE = 6.0846.
Fig. 7 and Fig. 8 shown below are comparison graph
plotted between desired output and simulated output
using simulated annealing genetic BPA neural
network for dataset of Daily IBM and Daily S&P
respectively. It can be observed from the graphs
when compared to graphs drawn for conventional
BPA in Fig. 5 and Fig. 6 that trend in the series are
better learned and approximated.
Figure 7: Graph for Daily IBM using Simulated Annealing
Genetic BPA network. Daily IBM Mean RMSE = 2.5426.
Figure 8: Graph for Daily S&P using Simulated Annealing
Genetic BPA network. Daily S&P = 5.4519.
Fig. 9 and Fig. 10 shown below are comparison
graph plotted between desired output and simulated
output using threshold acceptance genetic BPA
neural network for dataset of Daily IBM and Daily
S&P respectively. It can be observed from the
graphs when compared to graphs drawn for
conventional BPA in Fig. 5 and Fig. 6 that trend in
the series are better learned and approximated.
Figure 9: Graph for Daily IBM using Threshold
Acceptance Genetic BPA network. Daily IBM Mean
RMSE = 2.5321.
Figure 10: Graph for Daily S&P using Threshold
Acceptance Genetic BPA. Daily S&P = 5.6382.
4 CONCLUSIONS
A novel approach of financial forecasting using
simulated annealing and threshold acceptance is
proposed in this paper in order to obtain better
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
176

forecast results. Model is based on starting with
initialization of neural network and optimizing the
network parameter using traditional genetic
algorithm. Obtained network parameter is used as
starting seed point for simulated annealing and
threshold acceptance algorithm for further
optimizing the parameters in order to get global
optima. The proposed methodology comes out to be
an efficient as it gives better estimation of index
values. Proposed approach was compared with
traditional BPA algorithm. Empirical results
obtained as illustrated in section 3.3 for two of the
different financial time series concludes that
proposed approach gives a better results than
traditional BPA algorithm as can be seen in from
results in terms of average root mean square error. It
can also be drawn that from above results that
performance of simulated annealing and threshold
acceptance is financial time series specific, as
simulated annealing estimates better for Daily S&P
while threshold acceptance for Daily IBM.
REFERENCES
Zhou Yixin, Jie Zhang, "Stock Data Analysis Based on BP
Neural Network," ICCSN, pp.396-399, 2010 Second
International Conference on Communication Software
and Networks, 2010
Marzi, H.; Turnbull, M.; Marzi, E.; , "Use of neural
networks in forecasting financial market," Soft
Computing in Industrial Applications, 2008. SMCia
'08. IEEE Conference on, vol., no., pp.240-245, 25-27
June 2008
Ming Hao Eng; Yang Li; Qing-Guo Wang; Tong Heng
Lee; "Forecast Forex with ANN Using Fundamental
Data," Information Management, Innovation
Management and Industrial Engineering, 2008. ICIII
'08. International Conference on , vol.1, no., pp.279-
282, 19-21 Dec. 2008
P.Ram Kumar, M.V.Ramana Murthy , D.Eashwar ,
M.Venkatdas, “Time Series Modeling using Artificial
Neural Networks”, Journal of Theoretical and Applied
Information Technology Vol no.4 No .12, pp.1259-
1264, © 2005 - 2008 JATIT.
Zhizhong Zhao; Haiping Xin; Yaqiong Ren; Xuesong
Guo; , "Application and Comparison of BP Neural
Network Algorithm in MATLAB," Measuring
Technology and Mechatronics Automation
(ICMTMA), 2010 International Conference on , vol.1,
no., pp.590-593, 13-14 March 2010
Hossein Etemadi, Ali Asghar Anvary Rostamy, Hassan
Farajzadeh Dehkordi, A genetic programming model
for bankruptcy prediction: Empirical evidence from
Iran, Expert Systems with Applications, Volume 36,
Issue 2, Part 2, March 2009, Pages 3199-3207
Cheng-Xiang Yang; Yi-Fei Zhu; "Using genetic
algorithms for time series prediction," Natural
Computation (ICNC), 2010 Sixth International
Conference on, vol.8, no., pp.4405-4409, 10-12 Aug.
2010
Anupam Shukla, Ritu Tiwari, Rahul Kala, Real Life
Application of Soft Computing, CRC Press 2010.
Tsung-Lin Lee, Back-propagation neural network for the
prediction of the short-term storm surge in Taichung
harbor, Taiwan, Engineering Applications of Artificial
Intelligence, Volume 21, Issue 1, February 2008,
Pages 63-7
Elisaveta G. Shopova, Natasha G. Vaklieva-Bancheva,
BASIC--A genetic algorithm for engineering problems
solution, Computers & Chemical Engineering,
Volume 30, Issue 8, 15 June 2006, Pages 1293-1309
Abdusselam Altunkaynak, Sediment load prediction by
genetic algorithms, Advances in Engineering Software,
Volume 40, Issue 9, September 2009, Pages 928-934
B. Suman, P. Kumar, A Survey of Simulated Annealing as
a Tool for Single and Multiobjective Optimization,
The Journal of the Operational Research Society, Vol.
57, No. 10 (Oct., 2006), pp. 1143-1160
S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi,
“Optimization by simulated annealing,” Science, vol.
220, pp. 671–680, 1983.
Lidia, Steve; Carr, Roger; "Faster magnet sorting with a
threshold acceptance algorithm," Review of Scientific
Instruments , vol.66, no.2, pp.1865-1867, Feb 1995
Hung-Jie WANG, Ching-Jung TING, A Threshold
Accepting Algorithm for the Uncapacitated Single
Allocation p-Hub Median Problem, Journal of the
Eastern Asia Society for Transportation Studies,
Vol.8, 2009, pp. 802-814
Hipel and McLeod Time Series Modelling of Water
Resources and Environmental Systems, 1994, Elsevier.
Pepper, J.W.; Golden, B.L.; Wasil, E.A.; "Solving the
traveling salesman problem with annealing-based
heuristics: a computational study," Systems, Man and
Cybernetics, Part A: Systems and Humans, IEEE
Transactions on , vol.32, no.1, pp.72-77, Jan 2002
Abbas Khosravi, Saeid Nahavandi, Doug Creighton,
Construction of Optimal Prediction Intervals for Load
Forecasting Problems, IEEE Transactions on Power
Systems, vol.25, no. 3, pp. 1496-1503, Aug 2010
Jun Liu; Jiang Zhu; "Intelligent Optimal Design of
Transmission of Cooling Fan of Engine," Information
and Computing (ICIC), 2010 Third International
Conference on , vol.4, no., pp.101-104, 4-6 June 2010
Azlan Mohd Zain, Habibollah Haron, Safian Sharif,
Estimation of the minimum machining performance in
the abrasive waterjet machining using integrated
ANN-SA, Expert Systems with Applications, Volume
38, Issue 7, July 2011, Pages 8316-8326
FINANCIAL TIME SERIES FORECAST USING SIMULATED ANNEALING AND THRESHOLD ACCEPTANCE
GENETIC BPA NEURAL NETWORK
177
