SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION

OPERATORS FOR GENETIC ALGORITHMS

Ghodrat Moghadampour

Vaasa University of Applied Sciences, Wolffintie 30, 65200 Vaasa, Finland

Keywords: Evolutionary algorithm, Genetic algorithm, Function optimization, Mutation operator, Self-adaptive

mutation operators, Integer mutation operator, Decimal mutation operator, Fitness evaluation and analysis.

Abstract: Evolutionary algorithms are affected by more parameters than optimization methods typically. This is at the

same time a source of their robustness as well as a source of frustration in designing them. Adaptation can

be used not only for finding solutions to a given problem, but also for tuning genetic algorithms to the

particular problem. Adaptation can be applied to problems as well as to evolutionary processes. In the first

case adaptation modifies some components of genetic algorithms to provide an appropriate form of the

algorithm, which meets the nature of the given problem. These components could be any of representation,

crossover, mutation and selection. In the second case, adaptation suggests a way to tune the parameters of

the changing configuration of genetic algorithms while solving the problem. In this paper two new self-

adaptive mutation operators; integer and decimal mutation are proposed for implementing efficient

mutation in the evolutionary process of genetic algorithm for function optimization. Experimentation with

27 test cases and 1350 runs proved the efficiency of these operators in solving optimization problems.

1 INTRODUCTION

Evolutionary algorithms are heuristic algorithms,

which imitate the natural evolutionary process and

try to build better solutions by gradually improving

present solution candidates. It is generally accepted

that any evolutionary algorithm must have five basic

components: 1) a genetic representation of a number

of solutions to the problem, 2) a way to create an

initial population of solutions, 3) an evaluation

function for rating solutions in terms of their

“fitness”, 4) “genetic” operators that alter the

genetic composition of offspring during

reproduction, 5) values for the parameters, e.g.

population size, probabilities of applying genetic

operators (Michalewicz, 2000).

Genetic algorithm is an evolutionary algorithm,

which starts the solution process by randomly

generating the initial population and then refining

the present solutions through natural like operators,

like crossover and mutation. The behaviour of the

genetic algorithm can be adjusted by parameters,

like the size of the initial population, the number of

times genetic operators are applied and how these

genetic operators are implemented. Deciding on the

best possible parameter values over the genetic run

is a challenging task, which has made researchers

busy with developing even better and efficient

techniques than the existing ones.

2 GENETIC ALGORITHM

Most often genetic algorithms (GAs) have at least

the following elements in common: populations of

chromosomes, selection according to fitness,

crossover to produce new offspring, and random

mutation of new offspring.

A simple GA works as follows: 1) A population

-bit strings (chromosomes) is randomly

generated, 2) the fitness

)(xf

of each

chromosome

in the population is calculated, 3)

chromosomes are selected to go through crossover

and mutation operators with

and

probabilities

respectively, 4) the old population is replace by the

new one, 5) the process is continued until the

termination conditions are met.

However, more sophisticated genetic algorithms

typically include other intelligent operators, which

apply to the specific problem. In addition, the whole

algorithm is normally implemented in a novel way

with user-defined features while for instance

184

Moghadampour G..

SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS.

DOI: 10.5220/0003494401840191

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 184-191

ISBN: 978-989-8425-54-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

measuring and controlling parameters, which affect

the behaviour of the algorithm

2.1 Genetic Operators

For any evolutionary computation technique, the

representation of an individual in the population and

the set of operators used to alter its genetic code

constitute probably the two most important

components of the system. Therefore, an appropriate

representation (encoding) of problem variables must

be chosen along with the appropriate evolutionary

computation operators. The reverse is also true;

operators must match the representation. Data might

be represented in different formats: binary strings,

real-valued vectors, permutations, finite-state

machines, parse trees and so on. Decision on what

genetic operators to use greatly depends on the

encoding strategy of the GA. For each

representation, several operators might be employed

(Michalewicz, 2000). The most commonly used

genetic operators are crossover and mutation. These

operators are implemented in different ways for

binary and real-valued representations. In the

following, these operators are described in more

details.

2.1.1 Crossover

Crossover is the main distinguishing feature of a

GA. The simplest form of crossover is single-point:

a single crossover position is chosen randomly and

the parts of the two parents after the crossover

position are exchanged to form two new individuals

(offspring). The idea is to recombine building blocks

(schemas) on different strings. However, single-

point crossover has some shortcomings. For

instance, segments exchanged in the single-point

crossover always contain the endpoints of the

strings; it treats endpoints preferentially, and cannot

combine all possible schemas. For example, it

cannot combine instances of 11*****1 and

****11** to form an instance of 11***11*

(Mitchell, 1998). Moreover, the single-point

crossover suffers from “positional bias” (Mitchell,

1998): the location of the bits in the chromosome

determines the schemas that can be created or

destroyed by crossover.

Consequently, schemas with long defining

lengths are likely to be destroyed under single-point

crossover. The assumption in single-point crossover

is that short, low-order schemas are the functional

building blocks of strings, but the problem is that the

optimal ordering of bits is not known in advance

(Mitchell, 1998). Moreover, there may not be any

way to put all functionally related bits close together

on a string, since some particular bits might be

crucial in more than one schema. This might happen

if for instance in one schema the bit value of a locus

is 0 and in the other schema the bit value of the

same locus is 1. Furthermore, the tendency of

single-point crossover to keep short schemas intact

can lead to the preservation of so-called hitchhiker

bits. These are bits that are not part of a desired

schema, but by being close on the string, hitchhike

along with the reproduced beneficial schema

(Mitchell, 1998).

In two-point crossover, two positions are chosen

at random and the segments between them are

exchanged. Two-point crossover reduces positional

bias and endpoint effect, it is less likely to disrupt

schemas with large defining lengths, and it can

combine more schemas than single-point crossover

(Mitchell, 1998). Two-point crossover has also its

own shortcomings; it cannot combine all schemas.

Multipoint-crossover has also been implemented,

e.g. in one method, the number of crossover points

for each parent is chosen from a Poisson distribution

whose mean is a function of the length of the

chromosome. Another method of implementing

multipoint-crossover is the “parameterized uniform

crossover” in which each bit is exchanged with

probability

p , typically

8.05.0 ≤≤ p

(Mitchell,

1998). In parameterized uniform crossover, any

schemas contained at different positions in the

parents can potentially be recombined in the

offspring; there is no positional bias. This implies

that uniform crossover can be highly disruptive of

any schema and may prevent coadapted alleles from

ever forming in the population (Mitchell, 1998).

There has been some successful experimentation

with a crossover method, which adapts the

distribution of its crossover points by the same

process of survival of the fittest and recombination

(Michalewicz, 2000). This was done by inserting

into the string representation special marks, which

keep track of the sites in the string where crossover

occurred. The hope was that if a particular site

produces poor offspring, the site dies off and vice

versa.

The one-point and uniform crossover methods

have been combined by some researchers through

extending a chromosomal representation by

additional bit. There has also been some

experimentation with other crossovers: segmented

crossover and shuffle crossover (Eshelman and

SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS

185

Schaffer, 1991; Michalewicz, 2000). Segmented

crossover, a variant of the multipoint, allows the

number of crossover points to vary. The fixed

number of crossover points and segments (obtained

after dividing a chromosome into pieces on

crossover points) are replaced by a segment switch

rate, which specifies the probability that a segment

will end at any point in the string. The shuffle

crossover is an auxiliary mechanism, which is

independent of the number of the crossover points.

It 1) randomly shuffles the bit positions of the two

strings in tandem, 2) exchanges segments between

crossover points, and 3) unshuffles the string

(Michalewicz, 2000). In gene pool recombination,

genes are randomly picked from the gene pool

defined by the selected parents.

There is no definite guidance on when to use

which variant of crossover. The success or failure of

a particular crossover operator depends on the

particular fitness function, encoding, and other

details of GA. Actually, it is a very important open

problem to fully understand interactions between

particular fitness function, encoding, crossover and

other details of a GA. Commonly, either two-point

crossover or parameterized uniform crossover has

been used with the probability of occurrence

8.07.0 −≈p

(Mitchell, 1998).

Generally, it is assumed that crossover is able to

recombine highly fit schemas. However, there is

even some doubt on the usefulness of crossover, e.g.

in schema analysis of GA, crossover might be

considered as a “macro-mutation” operator that

simply allows for large jumps in the search space

(Mitchell, 1998).

2.1.2 Mutation

The common mutation operator used in canonical

genetic algorithms to manipulate binary strings

}1,0{),...(

=∈= Iaaa

of fixed length A was

originally introduced by Holland (Holland, 1975)

for general finite individual spaces

AAI ...

where

},...,{

iii

. By this definition, the

mutation operator proceeds by:

i. determining the position

}),...,1{(,...,

liii

∈

undergo mutation by a uniform random

choice, where each position has the same

small probability

p of undergoing mutation,

independently of what happens at other

position

ii. forming the new vector

),...,,,...,,,,...,(

1 A

aaa

hhh

+−

′

, where

∈

′

is drawn uniformly at random from the

set of admissible values at position

i .

The original value

a at a position undergoing

mutation is not excluded from the random choice of

Aa ∈

′

. This implies that although the position is

chosen for mutation, the corresponding value might

not change at all (Bäck, Fogel, Whitely, Angeline,

2000).

Mutation rate is usually very small, like 0.001

(Mitchell 1998). A good starting point for the bit-

flip mutation operation in binary encoding is

where

L is the length of the chromosome

(Mühlenbein, 1992). Since

corresponds to

flipping one bit per genome on average, it is used as

a lower bound for mutation rate. A mutation rate of

range

[

]

01.0,005.0∈

is recommended for binary

encoding (Ursem, 2003). For real-value encoding

the mutation rate is usually

[]

9.0,6.0∈

and the

crossover rate is

[

]

0.1,7.0∈

(Ursem, 2003).

Crossover is commonly viewed as the major

instrument of variation and innovation in GAs, with

mutation, playing a background role, insuring the

population against permanent fixation at any

particular locus (Mitchell, 1998), (Bäck et al., 2000).

Mutation and crossover have the same ability for

“disruption” of existing schemas, but crossover is a

more robust constructor of new schemas (Spears,

1993; Mitchell, 1998). The power of mutation is

claimed to be underestimated in traditional GA,

since experimentation has shown that in many cases

a hill-climbing strategy works better than a GA with

crossover (Mühlenbein, 1992; Mitchell, 1998).

While recombination involves more than one

parent, mutation generally refers to the creation of a

new solution form one and only one parent. Given a

real-valued representation where each element in a

population is an

n -dimensional vector

x ℜ∈

there are many methods for creating new offspring

using mutation. The general form of mutation can be

written as:

)(xmx

′

(1)

where

is the parent vector, m is the mutation

function and

′

is the resulting offspring vector. The

more common form of mutation generated offspring

vector:

Mxx +=

′

(2)

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

186

where the mutation

is a random variable.

has

often zero mean such that

xxE =

′

)( .

(3)

the expected difference between the real values of a

parent and its offspring is zero (Bäck et al., 2000).

Some forms of evolutionary algorithms apply

mutation operators to a population of strings without

using recombination, while other algorithms may

combine the use of mutation with recombination.

Any form of mutation applied to a permutation must

yield a string, which also presents a permutation.

Most mutation operators for permutations are related

to operators, which have also been used in

neighbourhood local search strategies (Whitley,

2000). Some other variations of the mutation

operator for more specific problems have been

introduced in Chapter 32 in (Bäck et al., 2000).

Some new methods and techniques for applying

crossover and mutation operators have also been

presented in (Moghadampour, 2006).

It is not a choice between crossover and mutation

but rather the balance among crossover, mutation,

selection, details of fitness function and the

encoding. Moreover, the relative usefulness of

crossover and mutation change over the course of a

run. However, all these remain to be elucidated

precisely (Mitchell, 1998).

2.1.3 Other Operators and Mating

Strategies

In addition to common crossover and mutation there

are some other operators used in GAs including

inversion, gene doubling and several operators for

preserving diversity in the population. For instance,

a “crowding” operator has been used in (De Jong,

1975), (Mitchell, 1998) to prevent too many similar

individuals (“crowds”) from being in the population

at the same time. This operator replaces an existing

individual by a newly formed and most similar

offspring. In (Mengshoel and Goldberg, 2008) a

probabilistic crowding niching algorithm in which

subpopulations are maintained reliably, is presented.

It is argued that like the closely related deterministic

crowding approach, probabilistic crowding is fast,

simple, and requires no parameters beyond those of

classical genetic algorithms.

The same result can be accomplished by using an

explicit “fitness sharing” function (Mitchell 1998),

whose idea is to decrease each individual’s fitness

by an explicit increasing function of the presence of

other similar population members. In some cases,

this operator induces appropriate “speciation”,

allowing the population members to converge on

several peaks in the fitness landscape (Mitchell,

1998). However, the same effect could be obtained

without the presence of an explicit sharing function

(Smith, Forrest and Perelson, 1993; Mitchell, 1998).

Diversity in the population can also be promoted

by putting restrictions on mating. For instance,

distinct “species” tend to be formed if only

sufficiently similar individuals are allowed to mate

(Mitchell, 1998). Another attempt to keep the entire

population as diverse as possible is disallowing

mating between too similar individuals, “incest”

(Eshelman and Schaffer, 1991; Mitchell, 1998).

Another solution is to use a “sexual selection”

procedure; allowing mating only between

individuals having the same “mating tags” (parts of

the chromosome that identify prospective mates to

one another). These tags, in principle, would also

evolve to implement appropriate restrictions on new

prospective mates (Eiben and Schut, 2008).

Another solution is to restrict mating spatially.

The population evolves on a spatial lattice, and

individuals are likely to mate only with individuals

in their spatial neighborhoods. Such a scheme would

help preserve diversity by maintaining spatially

isolated species, with innovations largely occurring

at the boundaries between species (Mitchell 1998).

The efficiency of genetic algorithms has also

been tried by imposing adaptively, where the

algorithm operators are controlled dynamically

during runtime (Eiben and Schut, 2008). These

methods cn be categorized as deterministic,

adaptive, and self-adaptive methods (Eiben and

Smith, 2007; Eiben and Schut, 2008). Adaptive

methods adjust the parameters’ values during

runtime based on feedbacks from the algorithm

(Eiben et al., 2008), which are mostly based on the

quality of the solutions or speed of the algorithm

(Smit and Eiben, 2009).

2.1.4 Other Operators and Mating

Strategies

In addition to common crossover and mutation there

are some other operators used in GAs including

inversion, gene doubling and several operators for

preserving diversity in the population. For instance,

a “crowding” operator has been used in (De Jong,

1975), (Mitchell 1998) to prevent too many similar

individuals (“crowds”) from being in the population

at the same time. This operator replaces an existing

individual by a newly formed and most similar

offspring. In (Mengshoel et al., 2008) a probabilistic

SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS

187

crowding niching algorithm in which

subpopulations are maintained reliably, is presented.

It is argued that like the closely related deterministic

crowding approach, probabilistic crowding is fast,

simple, and requires no parameters beyond those of

classical genetic algorithms.

The same result can be accomplished by using an

explicit “fitness sharing” function (Mitchell 1998),

whose idea is to decrease each individual’s fitness

by an explicit increasing function of the presence of

other similar population members. In some cases,

this operator induces appropriate “speciation”,

allowing the population members to converge on

several peaks in the fitness landscape (Mitchell,

1998). However, the same effect could be obtained

without the presence of an explicit sharing function

(Smith et al., 1993; Mitchell, 1998).

Diversity in the population can also be promoted

by putting restrictions on mating. For instance,

distinct “species” tend to be formed if only

sufficiently similar individuals are allowed to mate

(Mitchell 1998). Another attempt to keep the entire

population as diverse as possible is disallowing

mating between too similar individuals, “incest”

(Eshelman and Schaffer 1991; Mitchell, 1998).

Another solution is to use a “sexual selection”

procedure; allowing mating only between

individuals having the same “mating tags” (parts of

the chromosome that identify prospective mates to

one another). These tags, in principle, would also

evolve to implement appropriate restrictions on new

prospective mates (Eiben et al., 2008).

Another solution is to restrict mating spatially.

The population evolves on a spatial lattice, and

individuals are likely to mate only with individuals

in their spatial neighborhoods. Such a scheme would

help preserve diversity by maintaining spatially

isolated species, with innovations largely occurring

at the boundaries between species (Mitchell, 1998).

The efficiency of genetic algorithms has also

been tried by imposing adaptively, where the

algorithm operators are controlled dynamically

during runtime (Eiben et al., 2008). These methods

cn be categorized as deterministic, adaptive, and

self-adaptive methods (Eiben & Smith, 2007; Eiben

et al., 2008). Adaptive methods adjust the

parameters’ values during runtime based on

feedbacks from the algorithm (Eiben et al., 2008),

which are mostly based on the quality of the

solutions or speed of the algorithm (Smit et al.,

2009).

3 SELF-ADAPTIVE MUTATION

OPERATORS

One major problem with the classical

implementation of binary mutation, the multipoint

mutation or the crossover operator is that it is

difficult to control their effect or to restrict changes

caused by them within certain values.

Therefore, several techniques are developed here

to implement the genetic operators intelligently so

that the resulting modifications on the binary string

will cause changes in the real values within the

desired limits. This idea is implemented so that the

real value of the variable is randomly changed

within the desired limits and the modified value then

is converted to the binary representation and stored

as the value of the variable. In this way we can

cause more precise mutations in the bit strings and

make sure that changes in real values are within the

desired bounds.

Apparently, changes of different magnitudes are

required at different stages of the evolutionary

process. Thus, two types of decimal mutation

operators have been implemented:

1. For modifying variables with integer

values. The bounds for the absolute values of

such changes are at least 1 and at most the

integer part of the real value representation of

the variable. This means that the upper bound

of the range may vary even for each variable

of the same individual. The randomly

selected mutation value may be either

positive or negative. Thus, if the integer part

of the variable is

)int(variable , the integer

mutation range is

)int(var,1 iable±

2. For modifying variables with values from

the range

(

)

1,0 . The lower bound for the

absolute value of such changes is determined

by the required precision of the real value

presentation of the variable, like

6−

. The

upper bound for the absolute value of such

changes is determined by decimal part of the

variable. Here also the mutation value can be

either positive or negative. Thus, if the

number of digits after the decimal point for a

variable is

)varprecision( iable , and the decimal

part of the variable is

)rdecimal(va iable , the

range for the real mutation values is

[

]

)rdecimal(va ,

)varprecision(

iable

iable−

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

188

3.1 The Integer Mutation Operator

The integer mutation (IM) operator mutates the

individuals of the population in relatively great

magnitudes. This operator is naturally applied only

to individuals with integer part equal or greater or

than 1. During this operation an integer mutation

value

Δ is selected randomly from the following

range:

[

]

)(nti ,1 variable±∈Δ

(4)

and added to the variable under mutation. Here,

)(nti variable

stands for the absolute value of the

integer part of the variable. Clearly, this integer part

does not necessarily cover the whole range of the

variable. To avoid wasting resources special care is

taken to make sure that the generated random

number is not 0. Thus, the upper bound for the

integer mutation value is different for each variable

and is defined by the absolute value of the integer

part of the variable. This will make the process more

flexible and smart. If the resulting value of the

variable is outside of its pre-defined variable range,

the change will be rejected.

If the upper bound of the mutation value is set to

a fixed value, the operator becomes inefficient or the

probability for its failure will rise. For instance, if

the optimal value of a variable is 0.05 and its present

value 80.64, we will need 80 successful integer

mutations of magnitude 1 in order to get close to the

optimal value of the variable. However, if the

magnitude of the integer mutation value can be

dynamically determined by the magnitude of the

variable, the operator will have a much greater

chance to improve the value of the variable

dramatically in a short time.

During this operation a randomly generated

integer number within the specified bounds is added

to the value of the variable and the binary

representation of the resulting offspring is updated.

The offspring is then evaluated and put through the

survivor selection procedure. There is no fixed rate

for this operator. All population members go

through this operator at least once.

3.2 The Decimal Mutation Operator

The decimal mutation (DM) operator is used in

order to implement changes of smaller magnitudes

on individuals. This operator is naturally applied

only to variables with decimal part greater than 0.

During this operation non-zero decimal numbers in

the specific range are randomly generated and added

to the randomly selected variables in the individual.

The upper bound for the decimal mutation values is

determined by the absolute value of the decimal part

of variables. If the decimal part of a variable is

denoted by

)decimal(variable

, the maximum distance

of the mutation values from 0 is

)decimal(variable

The lower bound of the mutation range is

determined by the number of digits after the decimal

point. Thus, if

)precision(variable shows the number

of required decimal places of a variable, the decimal

mutation value is determined in the following way:

[

]

)rdecimal(va ,

)varprecision(

iable

iable−

(5)

If the resulting value of the variable is outside of

the pre-defined range of the variable, the change

will be rejected. The difference between this

operator and the integer mutation operator is the

way the mutation value is determined. Otherwise,

these operators are similar.

After each operator application, new offspring

are evaluated and compared to the population

individuals. Newly generated offspring will replace

the worst individual in the population if they are

better than the worst individual. Therefore, the

algorithm is a steady state genetic algorithm.

4 EXPERIMENTATION

The self-adaptive integer and decimal mutation

operators were applied as part of a genetic algorithm

to solve the following minimization problems:

Ackley’s function, Colville’s function, Griewank’s

function F1, Rastrigin’s function, Rosenbrock’s

function and Schaffer’s F6 and F7 functions. For

multidimensional problems with optional number of

dimensions (

), the algorithm was tested for

50 ,10 ,5 3, ,2 ,1

. The population size was set to 9.

The efficiency of the proposed operators was

compared against classical crossover (with 55%-

88% crossover rate) and mutation operator (with 1%

mutation rate). Experimentations were carried out

with three different configurations. In the first

configuration only classical mutation and crossover

operators were used to solve the problems. In the

second configuration classical mutation and

crossover and proposed self-adaptive integer and

decimal mutation operators were used to solve the

problems. Finally, in the third configuration only

proposed self-adaptive integer and decimal mutation

operators were used to solve the problems. For each

SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS

189

configuration the worst individual in the population

was replaced by a better offspring produced as a

result of applying an operator. Each algorithm was

run 50 times for each problem.

The following table summarises the results of

applying three different sets of operators to solve

functions mentioned earlier. Functions and different

variations of their variables make 27 different test

cases.

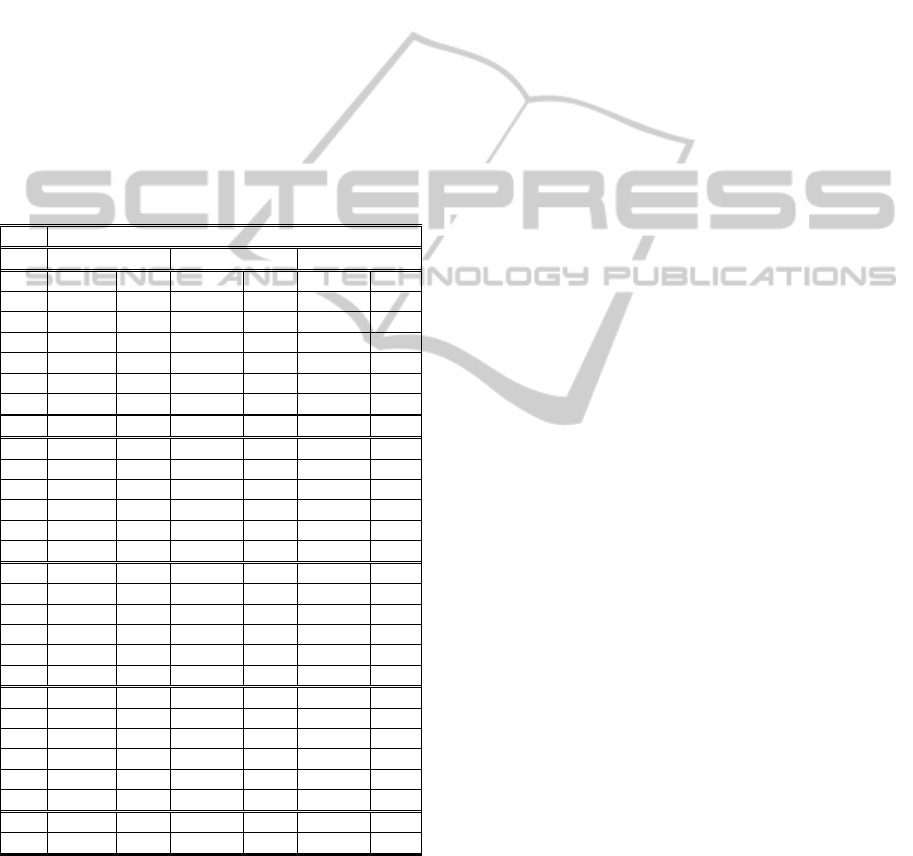
Table 1: Summary of test runs with three different

operator sets: CoMu (crossover & mutation), CoMuImDm

(crossover, mutation, integer mutation & decimal

mutation) and ImDm (integer mutation & decimal

mutation) to solve Ackely’s functions (A1-A50),

Colville’s function (C4), Grienwank’s functions (G1-

G50), Rastrigin’s function (Ra1-Ra50), Rosenbrock’s

function (Ro1-Ro50), Schaffer’s F6 (S62) and F7 (S72)

functions. Fn. stands for function, F. for fitness and FE.

for function evaluation.

Fn.

Operator Set

CoMu CoMuIm_Dm ImDm

F. FE. F. FE. F. FE.

A1 1.12E-06

5804 8.00E-08 3276 4.00E-06

10005

A2 2.98E-01

10017 1.76E-06 8174 4.00E-06

10005

A3 1.440

10009 8.30E-01 9844 8.02E-01

10006

A5 4.390

10015 0.278 10010 1.89

10006

A10 9.495

10009 1.188 10011 3.86

10006

A50 18.754

10019 8.925 10013 10.17

10005

C4 5.486

10012 0.564 5380 1.57

6688

G1 1.10E-03

5960 0.000 1740 7.89E-04

2723

G2 0.022

9998 0.017 9391 0.036

9644

G3 0.147

10017 0.110 10012 0.633

10005

G5 0.911

10007 0.531 10008 1.273

10004

G10 5.412

10006 2.860 10014 5.248

10006

G50 349.603

10018 56.67 10005 88.485

10006

Ra1 0.000

2650 0.000 494 0.00E+00

177

Ra2 0.073

9772 0.000 1111 0.00E+00

695

Ra3 0.593

10020 0.000 1867 0.239

4268

Ra5 2.951

10014 0.388 6300 2.688

9617

Ra10 19.720

10020 3.987 9417 9.830

10006

Ra50 149.98

10154 119.41 10076 114.50

10008

Ro1 0.000

18 6.46E-06 9832 5.56E-05

10008

Ro2 11.61

10013 5.32E-04 8259 3.56E-05

8474

Ro3 39.21

10010 0.111 10008 1.48

10008

Ro5 1.96E+04

10006 55.95 10012 116.87

10008

Ro10 3.29E+04

10011 1576 10026 9651

10008

Ro50 8.55E+07

10112 3.87E+05 10144 4.58E+07

10006

S62 1.07E-02

8746 5.05E-03 6822 3.69E-03

4807

S72 5.28E-02

7976 0.00E+00 780 0.00E+00

388

Studying results in Table 1 reveals that the

integer and decimal mutation operators have

successfully managed to improve the efficiency of

the algorithm either by decreasing the required

number of function evaluations or improving the

quality of the solutions or by resulting in both

improvements simultaneously. Using the integer and

decimal mutation operators in conjunction with

classical crossover and mutation operators resulted

in better fitness values in 93% of test cases and in

less required function evaluations in 74% of test

case. Furthermore, using integer and decimal

mutation operators in combination with the

crossover and mutation operator improved the

quality of the solution by at least 90% in 44% of test

cases.

The integer and decimal mutation operators

proved to outperform the classical crossover and

mutation operators in 78% of test cases in terms of

the quality of the solution and in 85% of test cases

in terms of required function evaluations. In 56% of

test cases the integer and decimal mutation operators

resulted in at least 50% of improvement in the

quality of solutions than the classical crossover and

mutation operators.

5 CONCLUSIONS

Two new genetic operators namely integer and

decimal mutation operators were proposed in this

paper. The operators were described and tested for

solving some classical minimization problems.

Furthermore, the efficiency of the proposed

operators against the classical crossover and

mutation operators was tested. Experimentation

proved that the proposed operators are efficient and

can lead into better results in solving optimization

problems.

REFERENCES

A. Eiben and J. Smith 2007. Introduction to Evolutionary

Computing. Natural Computing Series. Springer, 2nd

edition.

Bäck, Thomas, David B. Fogel, Darrell Whitely & Peter J.

Angeline 2000. Mutation operators. In: Evolutionary

Computation 1, Basic Algorithms and Operators. Eds

T. Bäck, D. B. Fogel & Z. Michalewicz. United

Kingdom: Institute of Physics Publishing Ltd, Bristol

and Philadelphia. ISBN 0750306645.

De Jong, K. A. 1975. An Analysis of the Behavior of a

Class of Genetic Adaptive Systems. Ph.D. thesis,

University of Michigan. Michigan: Ann Arbor.

Eshelman, L. J. & J. D. Schaffer 1991. Preventing

premature convergence in genetic algorithms by

preventing incest. In Proceedings of the Fourth

International Conference on Genetic Algorithms. Eds

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

190

R. K. Belew & L. B. Booker. San Mateo, CA: Morgan

Kaufmann Publishers.

G. Eiben and M. C. Schut 2008. New Ways To Calibrate

Evolutionary Algorithms. In Advances in

Metaheuristics for Hard Optimization, pages 153–177.

Holland, J. H. 1975. Adaptation in Natural and Artificial

Systems. Ann Arbor: MI: University of Michigan

Press.

Mengshoel, Ole J. & Goldberg, David E. 2008. The

crowding approach to niching in genetic algorithms.

Evolutionary Computation, Volume 16, Issue 3 (Fall

2008). ISSN:1063-6560.

Michalewicz, Zbigniew 2000. Introduction to search

operators. In Evolutionary Computation 1, Basic

Algorithms and Operators. Eds T. Bäck, D. B. Fogel

& Z. Michalewicz. United Kingdom: Institute of

Physics Publishing Ltd, Bristol and Philadelphia.

ISBN 0750306645.

Mitchell, Melanie 1998. An Introducton to Genetic

Algorithms. United States of America: A Bradford

Book. First MIT Press Paperback Edition.

Moghadampour, Ghodrat 2006. Genetic Algorithms,

Parameter Control and Function Optimization: A New

Approach. PhD dissertation. ACTA WASAENSIA

160, Vaasa, Finland. ISBN 952-476-140-8.

Mühlenbein, H. 1992. How genetic algorithms really

work: 1. mutation and hill-climbing. In: Parallel

Problem Solving from Nature 2. Eds R. Männer & B.

Manderick. North-Holland.

S. K. Smit and A. E. Eiben 2009. Comparing Parameter

Tuning Methods for Evolutionary Algorithms. In

IEEE Congress on Evolutionary Computation (CEC),

pages 399–406, May 2009.

Smith, R. E., S. Forrest & A. S. Perelson 1993. Population

diversity in an immune system model: implications for

genetic search. In Foundations of Genetic Algorithms

2. Ed. L. D. Whitely. Morgan Kaufmann.

Spears, W. M. 1993. Crossover or mutation? In:

Foundations of Genetic Algorithms 2. Ed. L. D.

Whitely. Morgan Kaufmann.

Ursem, Rasmus K. 2003. Models for Evolutionary

Algorithms and Their Applications in System

Identification and Control Optimization (PhD

Dissertation). A Dissertation Presented to the Faculty

of Science of the University of Aarhus in Partial

Fulfillment of the Requirements for the PhD Degree.

Department of Computer Science, University of

Aarhus, Denmark.

Whitley, Darrell 2000. Permutations. In Evolutionary

Computation 1, Basic Algorithms and Operators. Eds

T. Bäck, D. B. Fogel & Z. Michalewicz. United

Kingdom: Institute of Physics Publishing Ltd, Bristol

and Philadelphia. ISBN 0750306645.

SELF-ADAPTIVE INTEGER AND DECIMAL MUTATION OPERATORS FOR GENETIC ALGORITHMS

191