MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR

ENERGY EFFICIENCY AND LIFETIME MAXIMIZATION

IN WIRELESS SENSOR NETWORKS

H. Sivasankari, Vallabh M., Shaila K. and K. R. Venugopal

University Visvesvaraya College of Engineering, Bangalore University, Bangalore 560 001, India

L. M. Patnaik

Vice Chancellor, Defence Institute of Advanced Technology (Deemed University), Pune, India

Keywords:

Energy efﬁciency, Lifetime maximization, Multiple mobile sink, Sojourn time and wireless sensor networks.

Abstract:

Wireless Sensor Networks(WSNs) consist of battery operated sensor nodes. Improving the lifetime of sensor

network is a critical issue. Nodes closer to the sink node drains energy faster due to large data transmission

towards a sink node. This problem is resolved through mobility of the sink node. The Mobile sink moves

to particular positions in predetermined order to collect data from the sensor nodes. There is considerable

delay in the case of single mobile sink. In this paper we have used the concept of multiple mobile sinks to

collect data in different zones which in turn coordinate to consolidate the data and complete the processing

of data received from all the sensor nodes. A distributed algorithm synchronizing all the mobile sinks are

used to reduce the delay in consolidation of data and reducing the overall energy consumption. The twin gain

increases the lifetime of the Wireless Sensor Network. Simulation results using Multiple Mobile Synchronized

Sinks clearly shows that there is an increase of 28% and 56% in the lifetime of the Wireless Sensor Networks

in comparison with Single Mobile Sink and Static Sink respectively.

1 INTRODUCTION

Wireless Sensor Network (WSNs) uses battery op-

erated wireless micro-sensor nodes to collect the in-

formation from a geographical ﬁeld and transmits in

multihops to the sink. Hundreds or thousands of this

micro-sensors are deployed to watch the environment

and collects the data about it. These sensor batteries

are impractical to replace or recharge and hence en-

ergy of the sensor nodes are to be saved to increase

the lifetime of the Network. The operational lifetime

of a sensor node is in terms of weeks or months. Sen-

sor node spends energy for each process like sensing,

transmitting and receiving data. Hence, energy is an

important criteria in Wireless Sensor Networks.

WSNs have considerable technical challenges in

data processing and communication to deal with dy-

namically changing Energy, Bandwidth, Delay, Sens-

ing and Processing power. The vital issue in WSNs

is to maximize the network operational life. In order

to achieve this, it is necessary to minimize the energy

utilization of every sensor node. Energy can be conse-

rved by efﬁcient routing and data aggregation. An-

other important issue in WSNs is security when it op-

erates in a hostile environment and needs to be pro-

tected against intruders.

For the small networks, source sensors can di-

rectly transmits the data to the sink node. For a larger

network, multihop communication is needed to reach

the static sink. For real time applications, the sensi-

tive data should reach the sink node without any de-

lay. There are many methods to reduce the distance

between the source and the sink. First method is to

move the sink node over the entire network to collect

the data, the second method is to have multiple static

sinks at different locations and third method is to in-

crease the number of mobile sinks. Thus the distance

between the source and sink is reduced.

When an event occurs, immediately the sensor

node communicates the information to the sink node.

Neighbor nodes of the sink node depletes energy

faster due to the large and continuous data forward-

ing towards the sink. Thus, lifetime of the sensor

network is reduced even though non-neighbor nodes

Sivasankari H., M. V., K. S., R. Venugopal K. and M. Patnaik L..

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND LIFETIME MAXIMIZATION IN WIRELESS SENSOR

NETWORKS.

DOI: 10.5220/0003499500760085

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 76-85

ISBN: 978-989-8425-56-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

haveenough energy for communication. To overcome

this problem Gatzianas et al., (Gatzianas and Geor-

giadis, 2008) have considered the use of single mo-

bile sink. The mobile sink collects the information

from the sensor nodes during its round trip time i.e.,

time during which mobile sink visits entire network

in predetermined positions.

Motivation. In static sink sensor network, nodes

closer to the sink depletes their energy fast, though

other nodes in a network have enough amount of

energy for communication. The single mobile sink

keeps moving to predetermined positions and stays

for a speciﬁc period of time to collect the data. The

sensitive data moving from the source sensors may

loose their importance due to the nonavailability of

the single mobile sink. This is due to the delay in

the arrival of the single mobile sink to that position.

This problem is addressed in this paper by implement-

ing distributed algorithm with multiple mobile sinks

and thus sensitive information reaches the sink with-

out delay.

Contribution. The main contribution of this paper

is the development of an efﬁcient distributed algo-

rithm using Multiple Mobile Synchronized Sinks of-

fering an alternative to the single mobile sink. A dis-

tributed algorithm for computing the maximum life-

time of a wireless sensor network, which routes data

to the nearest mobile sink by imposing ﬂow con-

servation to all positions with respect to sinks. An

interference-free sensor network with a multiple mo-

bile synchronized sinks reduces delay, uses less Band-

width, consumes lower energy and increases the life-

time of the WSNs.

Organization. The rest of the paper is organized as

follows: Related work and Background work are dis-

cussed in Section 2 and Section 3 respectively. Sys-

tem Model and Network Architecture are explained

in Section 4. Problem Deﬁnition and Mathematical

Model is formulated in Section 5. Algorithm is de-

veloped in Section 6. Simulation and Performance

parameters are analyzed in section 7. Conclusions are

presented in Section 8.

2 RELATED WORK

Gatzians et al.,(Gatzianas and Georgiadis, 2008) ad-

dressed the maximization of lifetime of a mobile sink

WSNs in-terms of energy constraint. A distributed

Synchronous ε -relaxation algorithm based on the

subgradient method is presented to minimize the re-

quired time to route data from other nodes of the net-

work to a mobile sink. The system is restricted to

semi-deterministic settings resulting in considerable

delay.

Michail et al.,(Michail and Ephremides, 2003)

discussed the routing connection-oriented trafﬁc in

wireless sensor networks with energy efﬁciency. Min-

imization of data transmission cost with limited band-

width resources have been considered. Real-time con-

straints in the system and the restriction of nodes to

the boundary of location leads to long routing paths

between end to end nodes.

Xiao et al.,(Xiao et al., 2004) focused on link

based optimal routing in wireless data networks. They

have exploited a Simultaneous Routing Resource Al-

location (SRRA) problem and capacitated multicom-

modity ﬂow model to describe the data ﬂows in the

WSN. Joint link scheduling, routing and power allo-

cation are not emphasized in this work.

Chang et al.,(Chang and Tassiulas, 2000) consid-

ered ﬂow augmentation, ﬂow redirection algorithm to

balance the energy among the nodes in proportion to

their reserve energy. The robustness of Shortest path

routing to maximize the lifetime of a network is not

discussed in this work.

Madan et al.,(Madan and Lall, 2006) formulated

a distributed algorithm to compute an optimal routing

scheme. The algorithm derived the concept of convex

quadratic optimization & time constraint to maximize

the lifetime of network. They have not considered

asynchronous sub-gradient algorithm.

Ritesh et al.,(Madan et al., 2005) discussed the

mixed integer convex program to maximize the life-

time of network. Non linear class of interference

free Time Division Multiple Access for load balanc-

ing, Multihop routing frequency reuse & interference

mitigation are utilized to increase lifetime of net-

work. The work is restricted for non-distributed low

topologised model with lower bound. Shashidhar et

al.,(Gandham et al., 2003)proposed a ﬂow based rout-

ing protocol to minimize the energy consumption in

the sensors of WSNs.

Weiwang et al., (Weiwang and Chua, 2005) have

used mobile relays to prolong the lifetime of Wireless

Sensor Networks. The lifetime of the dense sensor

network with mobile sink and mobile relays are al-

most same as that of mobile sink.

Branislav et al.,(Kusy et al., 2009) have developed

an algorithm for data delivery in mobile sensor net-

works. Mobility patterns in the network, enables the

algorithm to maintain an uninterrupted data stream.

Scalability and communication cost are not consid-

ered.

Huang Zhi et al., (Zhi et al., 2010) have developed

routing strategies for Dynamic WSN with single sink

and multiple sinks. DWSN with single static sink is

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND

LIFETIMEMAXIMIZATION INWIRELESS SENSOR NETWORKS

more reliable than the multiple static sinks. Frequent

changes of routing table consumes more energy and

the lifetime of Dynamic WSN is reduced with long

latency and weak reliability.

Getsy et al.,(Getsy et al., 2010) proposed cluster

based routing protocol for Mobile WSN (MWSN).

Bayes rule is used in selection of cluster head with

highest energy, least mobility and best transmission

range. It is not fault tolerant.

3 BACKGROUND

Nodes in a Wireless Sensor Network produces infor-

mation at a deterministic rate. Sensor Nodes nearer

to the static sink, drains energy soon because of large

data transmission to the sink node. To increase the

lifetime of the sensor network Luo et al.,(Luo et al.,

2005) considered a single mobile sink. Each node

drains energy as the mobile sink moves to close to a

position of occurrence of an event, spends a speciﬁed

amount of time to collect the data from the sensors

around the location of occurrence of the event.

The following conditions are assumed to give fea-

sible solutions to the outgoing links of node to max-

imize the lifetime. The total expended power should

not exceed the initial reserve energy. A peak power

transmission constraints are imposed in all the loca-

tion of sink and time intervals. A mobile sink can re-

side in a particular location for nonzero sojourn time

and when sojourn time becomes zero, it moves to the

next location.

In a distributed algorithm each node must store

the following information., (i) Sink is distinguished

from other nodes by unique node tag identiﬁer,(ii)

The maximum rate of information, energy and in-

stantaneous power for each node, (iii) group of vari-

ables representing the ﬂow and ﬂow conservation cost

which are used in minimum cost ﬂow algorithm. (iv)

the outgoing and incoming edges are doubly linked

list, (v) a maximum array length to store parent and

children of the node, (vi) variables independent of

Network size.

4 SYSTEM MODEL AND

NETWORK ARCHITECTURE

4.1 Deﬁnitions

Mobile Sink. One mobile sink moves to the pre-

determined positions collecting data from all the

neighboring nodes.

Synchronized Sinks. Synchronization of multiple

mobile sink is achieved through the common no-

tion of time.

Multiple Mobile Sinks. More than one mobile sink

moves to the predetermined positions collecting

data from all the neighboring nodes.

Sojourn Time. The duration of time during which

active mobile sink resides in a particular position.

Network Alive. The Network is alive until the sen-

sor can transfer all generated trafﬁc to the nearest

sink by satisfying the energy/power and ﬂow con-

servation constraints.

Energy Consumption. The amount of energy spent

by each node in a sensor network for sensing,

sending, receiving and processing data.

Lifetime of a Network. The period of time until the

ﬁrst node runs out of energy.

Delay. Time taken by the data to reach the mobile

sink node from the source sensor node.

4.2 Network Architecture

The Multiple Mobile Synchronized Sink WSNs con-

sists of two types of nodes, (i) Static ordinary sensor

nodes which can only capture and transmit data, (ii)

Mobile sink nodes that move to predetermined po-

sitions to collect data from the static Sensor nodes.

Multiple mobile sink nodes can coordinate to con-

solidate data collected from the static sensor nodes.

The Wireless Sensor Network is divided into a num-

ber of zones as shown in Figure 1. The movement

of the mobile sink is restricted to its zone. This tech-

nique increases the collection of data from ordinary

sensor nodes reducing the consumption of energy and

delay. Both these features helps in increasing the life-

time of WSNs. When one of the sink fails, the zones

are merged. The network still continues to function

though at a reduced efﬁciency, there is increase in

delay and is called graceful degradation. The em-

ployment of multiple mobile sink increases reliabil-

ity and does not allow the WSNs to collapse even

with the failure of some Mobile sinks. The multiple

mobile sinks are in continuous communication syn-

chronously and thereby any failure in the sinks will

be immediately detected and can be rectiﬁed.

4.3 Network Model

Consider a Wireless Sensor Network consisting of

battery operated static nodes, which are randomly de-

ployed over a given geographical area. The system

model for the mobile sinks x

, moves to ﬁxed position

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

0 10 20 30 40 50 60 70 80 90 100

100

Ordinary Node

Mobile Sink Node

Figure 1: Basic Multiple Mobile Sink Wireless Sensor Net-

work Architecture.

to avoid early energydissipation of neighbor nodes

of the sink (i.e., as in static sensor network)(Luo,

2006). Each node sensor i = 1,.......,n ∈ V produces

a ﬁxed amount of information at rate of I

≥ 0. It is

assumed that all links between the nodes are bidirec-

tional. The notations used in this paper are deﬁned in

Table 1.

The movement of the sinks to different positions

creates a subgraph G(V,L). All nodes i ∈ V except for

the sink are equipped with a non-renewable amount

of energy E

> 0. The energy of the sensor is gradu-

ally depleted as the nodes participate in routing. Once

a node’s energy is drained, the node can no longer

transmit which leads to network failure.

5 PROBLEM DEFINITION AND

MATHEMATICAL MODEL

5.1 Problem Deﬁnition

Given a set of Wireless Sensor Nodes i ∈ V, where

i = 1,......, n and set of mobile sinks, t

the sojourn

time of the m

sink at position p, t

p,k

for a set of

iterations where k = 1, .....,K. The objectives are

1. To decrease energy consumption and increase the

lifetime of the Wireless Sensor Network.

2. To ﬁnd optimal routing, maintain synchronization

between the mobile sinks, to improve sojourntime

and increase the survival time of the network (T).

Where

max T =

∑

k=1

p,k

(1)

Table 1: Notations.

G Undirected Graph.

V Set of sensor nodes.

L Edge set or link set.

Source node i, i = 1,...,n.

mobile sink.

i Single sensor node, i ∈ V.

set of outgoing neighbors of node i

at sink at position p.

Information generated at the node i.

position of the mobile sink x

, p ∈ P.

P set of mobile sinks positions.

p,k

Data transmission rate from node i to j

while sink stays at position p for k

iteration.

Data transmission rate from node i to j

while sink stays at position p.

p,k

Time for k

iteration of m

mobile sink

at position p.

p,k

Power needed for data transmission from

node i to j while sink stays at position p

for k

iteration.

Power needed for data transmission from

node i to j while sink stays at position p.

Sojourn time of the m

sink at position p.

Initial Energy of the node.

′

Sub graph G

′

⊂ G.

Power needed for transmitting one bit of

data.

Power needed for receiving one bit of data.

k bits of data is received.

k bits of data is transmitted.

α transmission factor.

β reception factor.

power constraint

distance between node i and j

and can be further reduced to a equivalent form of

max T =

∑

(2)

From Equation 2, we can calculate the maximum

lifetime of each mobile sink at different positions.

Assumptions

1. Sensor nodes are stationary, but the sinks change

their positions from time to time with negligible

traveling time between two positions. The posi-

tions of the sinks can be chosen within a ﬁnite set

of x

∈ P.

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND

LIFETIMEMAXIMIZATION INWIRELESS SENSOR NETWORKS

2. A mobile sink has long range of communication

that facilitates to transmit data.

3. Each sensor i ∈ V produces information at ﬁxed

deterministic rate I

≥ 0, which is routed in multi-

hops to one of the mobile sinks x

5.2 Mathematical Model

For receiving k

bits/sec, the power consumption at

sensor node is e

= k

β. where, β is reception factor

indicating the energy consumption per bit. The power

needed for transmitting k

bits/sec is e

= k

αd

where, α is transmission factor indicating the energy

consumption per bit and d

is the distance between

transmitting and receiving node. Therefore, total en-

ergy consumption at a node per time unit is

+ e

= k

β+ k

αd

≈ e(k

+ k

) (3)

where, e = β ≈ α d

, because energy consumed to

transmit a bit is approximately equal to the energy

consumed for receiving a bit.

From the above discussions, the energy consump-

tion at a sensor node i when the sink sojourn at posi-

tion p is computed as

= e(

∑

j∈S

∑

j:i∈S

) (4)

where, e

represents the total power needed for data

transmission from node i to j while sink stays at

position p. The energy is calculated through data

transmission rate from node i to j and j to i vice

versa with respect to the sink’s position.

∑

j ∈ S

≤ E

∀ i ∈ N (5)

∑

j ∈ S

≤ ε

, ∀ i ∈ N, ∀ p ∈ P (6)

∑

j∈S

= I

∑

j:i∈S

(7)

The sink is moving through robots. The entire geo-

graphical deploymentarea has dividedinto two zones.

In each zone sinks moves to the predeﬁned positions.

The mobile sink moves to different positions to col-

lect the data from the source node. When an event

occurs, the sensor senses the data and it forwards the

data to the nearest mobile sink positions. If sink is

not available in that position then sensors forwards the

data to the next available position of the sink. We re-

duce the Response Time (RT) by introducing the mul-

tiple mobile sinks. The Response Time is computed

as,

RT = RT

end

− RT

start

(8)

start

is the time during which the packet started.

end

is the time during which the packet reached the

sink.

Equation 4 represents the total amount of energy

spent at node i and j that depends on the trafﬁc rate

on node i and j. Equation 5 and 6 explains the energy

constraints for communication i.e., energy required

for transmitting and receiving data, must not exceed

the residual energy of a node. Equation 7 gives the

data transmission rate on link i, j i.e., the sum of ac-

tual sensed information and trafﬁc rate in the link.

6 ALGORITHM

6.1 MMSS Distribution Algorithm

The Multiple Mobile Synchronized Sink algorithm

comprises of two algorithms: MMSS Routing Algo-

rithm and MMSS Iteration Algorithm. In Table 2 the

MMSS Distribution Algorithm begins with the selec-

tion of multiple mobile sinks. Each sink moves to a

predeﬁned position for a speciﬁed period of time to

collect data from each zone. The neighbors of a ac-

tive sinks are identiﬁed by sending the hello packets

from all the sensor nodes to the nearest active sink.

MMSS algorithm runs for various iterations for dif-

ferent sinks and positions.

MMSS Routing Algorithm selects a minimum

distance routing to reduce the energy consumption in

the network. When a sensor node has data to forward,

it checks for the active sink position and then forwards

the data. If the data transmission time exceeds the

sink’s sojourn time then forwards the data to the next

nearest active position of the mobile sink.

The data collection during the sojourn time of the

mobile sink is referred as iterations (i.e., number of

successive transmission). Number of iterations for a

particular sink is computed by summing the number

of successive transmission during its round trip. The

amount of energy dissipated by each node for trans-

mission and reception of data is calculated. If residual

energy is equal to zero then network fails. Other-

wise, the algorithm runs until one of the node’s en-

ergy drains to zero in the network. Failure in the sink

is detected and repaired as the sinks are synchronized.

7 IMPLEMENTATION AND

PERFORMANCE ANALYSIS

In the setup of MATLAB simulation, a 100m x 100m

region was considered with three sets of network

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

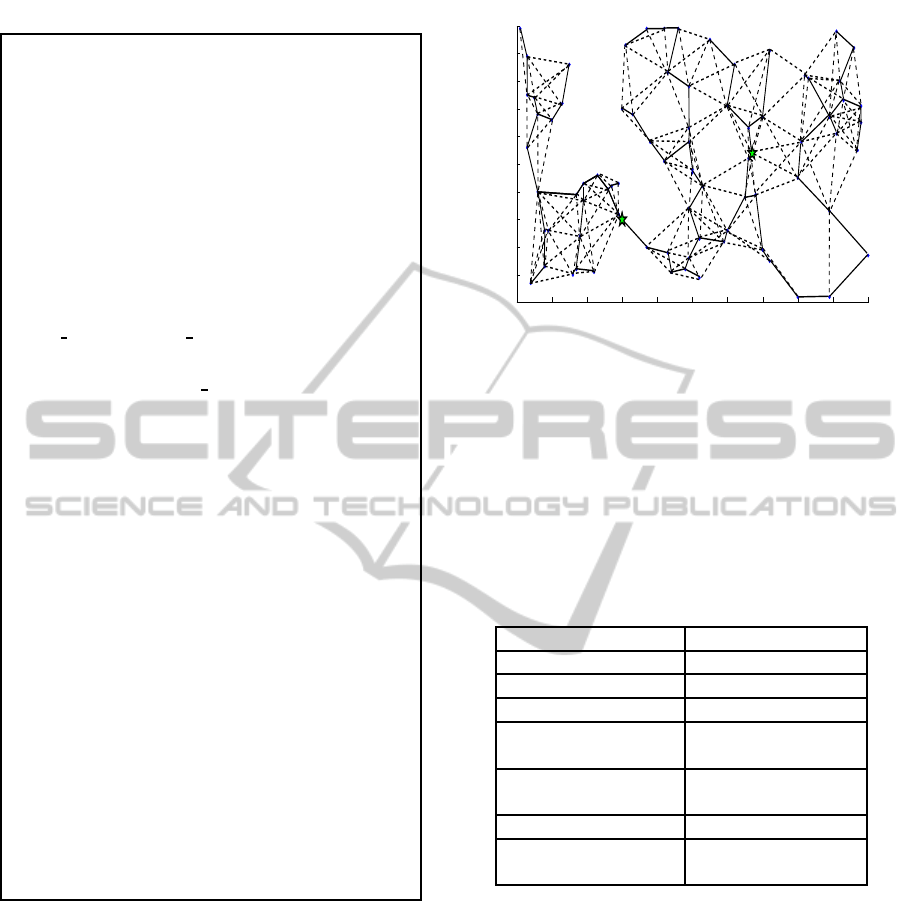
Table 2: MMSS Distribution Algorithm.

The subgraph G

′

∈ G for all k, vectors V,E, P,I,ε

initial iteration k

are taken as input to the algorithm

Initialize k = k

Select x

as the number of mobile sinks and predeter-

mine positions as x

Fix the routing path of each sink x

;

set arbitrary time t;

while termination criterion is false do

for p = 0 to |P| − 1 do

Phase 1: MMSS Routing Algorithm

for i = 1 to n− 1 do

for j = i+ 1 to n do

Calculate the distance between all the nodes with

respect to the active position of the sink x

at time t.

total distance = total distance+ distance ;

endfor

compute minimum total distance

solve the minimum cost ﬂow for subgraph G

′

determine t

;

if t

≥ transmission time then

Route the data to the nearest active position of the

sink x

else Route the data to the next nearest active position

of the sink x

endif

Phase 2: MMSS Iterations Algorithm

update t

∀(i, j) ∈ L

update from k to k + 1 for all nodes

endfor

Calculate Energy dissipation as

Energy dissipation = Transmission Power +

Flow Rate;

Calculate Residual energy of the node

= Residual Energy − Energy dissipation;

if E

= 0 then

return;

else

k = k + 1;

endif

if sink x

is failed then x

m+1

is made active for that

zone.

endif

endw

topology with 20, 40 and 80 nodes respectively. The

sink was allowed to move over 2, 4 and 8 locations,

which were the same for all zones. In all cases, each

node had an exogenous rate of I

= 1. The ﬂow cost of

edge L(i, j) is assumed proportional to d

the physi-

cal distance between the two nodes. Two scenarios

were studied: in the ﬁrst one, only a power constraint

of E

= 100nJ is applied while in the second one, a

power constraint of ε

= 10nJ is also imposed. The

simulation parameters are shown in Table 3.

We consider, as nodes increase in a sensor net-

works, the number of mobile sinks also increases. The

Simulation environment deployed with 8x10 i.e., 80

nodes. Each node is identiﬁed through node identi-

0 10 20 30 40 50 60 70 80 90 100

100

Figure 2: Complete Route tree for Multiple mobile sink in

100X100 area with 80 nodes.

ﬁer as node 1, node 2, node 3 etc... The simulation

setup is varied for 20, 40, 80 nodes with multiple mo-

bile sinks. Mobile sink moves in 2, 4, 8 locations and

stays for a sojourn time. We observe that, there is a

considerable increase in the lifetime of a multiple mo-

bile sink of Sensor Network in comparison with static

and single mobile sink.

Table 3: Simulation Parameters.

Parameter Type Test values

Number of nodes 100

sink node mote 1

Radio model lossy

Multi channel Radio 433MHz

Transceiver

Sensor type Light, Temperature,

Pressure

Outdoor Range 500ft

Energy consumption 60pJ

per bit

Table 4, Table 5 and Table 6 gives the amount of

energy residues in each node of 8x10 simulation setup

after 914, 1386 and 1646 iterations of Sensor Net-

work with static sink, single mobile sink and multiple

mobile sink respectively. Table 4 shows the residual

energy of nodes for single static sink. In the table

zeroth row and ﬁrst column represents node 1, the ze-

roth node and second column represent node 2 and

the ﬁrst row and ﬁrst column represent node 11 in this

manner nodes 1 to node 80 are identiﬁed. The amount

of energy residues in node 1 is 1.378nJ.

Table 4 gives the residual energy of the node for

the network with the static sink. We observe that

nodes 25, 36, 45 and 66 closer to the static sink have

zero energy remaining and the network fails after 914

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND

LIFETIMEMAXIMIZATION INWIRELESS SENSOR NETWORKS

0 10 20 30 40 50 60 70 80

Number of Sensor Nodes

Residual Energy in the sensor node(nJ)

MMSS

Figure 3: Comparison between the MMSS, SMS and SS Networks after 914 iterations.

Table 4: Residual Energy(nJ) in each node of 8x10 static sink WSNs after 914 iterations.

1 2 3 4 5 6 7 8 9 10

0 1.378 1.096 1.085 1.062 1.204 0.805 0.706 1.009 1.430 1.180

1 1.085 1.096 1.08 1.92 1.04 1.001 1.056 1.900 1.340 1.185

2 1.876 1.021 1.002 1.000 0.000 1.467 1.024 1.000 1.623 1.035

3 0.902 0.963 1.001 1.258 0.020 0.000 2.109 1.008 1.424 1.970

4 0.876 1.021 1.002 2.009 0.000 1.467 1.024 0.767 1.623 1.035

5 1.402 1.125 1.535 0.952 0.890 1.060 1.003 1.800 0.873 0.803

6 1.085 0.086 1.007 1.802 1.401 0.000 0.996 0.989 1.230 0.623

7 1.376 1.823 1.009 1.037 1.726 1.004 1.078 1.009 1.009 0.543

iterations.

Table 5 gives the residual energy of the network

with single mobile sink. Node 13, 16, 24, 25, 35, 36,

46, 47, 48 and 69 have zero energy after 1386 itera-

tions where further communication is not possible.

Table 6 represents the residual energy of the net-

work with multiple mobile sink. In this table node 8,

16, 23, 36, 39, 44, 45, 48, 52, 63, 66, 74 and 78 has

zero energy after 1646 iterations. Table 7 explains the

lifetime of the variable networks size. For 10 nodes

with static sink network, the lifetime is only 143 it-

erations which is less than that network with single

mobile sink and multiple mobile sink. As the number

of nodes increase in a given area, the lifetime also in-

creases.

Figure 2 shows the complete routing tree for mul-

tiple mobile sinks. This shows that energy at all nodes

are used effectively through multiple mobile sinks,

Thus it increases the lifetime of the network.

Figure 3 explains the amount of energy residues

in each node for the same deployment of 8x10 after

914 iterations for Sensor Networks with static sink,

single mobile sink and multiple mobile sink. It is ob-

served that residual energy is higher in each node of

that multiple mobile sink than with the static sink and

single mobile sink.

0 0.5 1 1.5 2 2.5 3 3.5 4

Number of Mobile Sink

Network Lifetime (weeks)

MMSS

OPTIMAL POINT

Figure 4: Optimal number of sinks for a 80 node network.

The variance of residue energy in WSN with static

sink is 0.2578. The variance of residue energy in

WSN with static sink is 0.2295. The variance of the

residual energy in the network with multiple mobile

sinks is 0.2235, which is lower than the network with

the static and single mobile sink. It is observed that

all nodes in MMSS network, drain their energy uni-

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

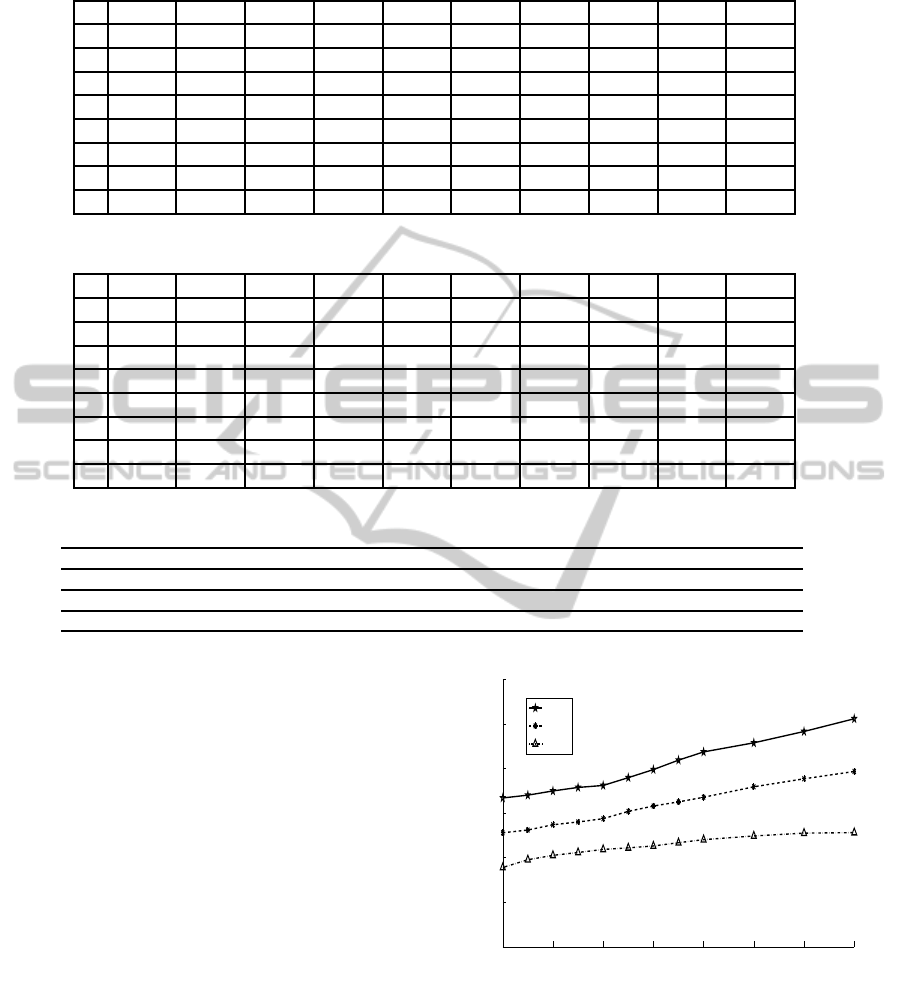
Table 5: Residual Energy(nJ) in each node of 8x10 Single Mobile Sink WSNs after 1386 iterations.

1 2 3 4 5 6 7 8 9 10

0 0.096 0.003 0.009 0.036 0.826 1.104 0.778 0.209 0.009 0.518

1 0.085 0.086 0.000 0.002 1.004 0.000 0.096 0.020 0.230 0.623

2 0.876 1.021 1.002 0.000 0.000 1.467 0.024 1.000 0.623 1.035

3 0.002 0.25 0.535 0.952 0.000 0.000 0.003 0.800 0.873 0.803

4 1.378 0.096 0.085 1.072 0.204 0.000 0.000 0.000 0.430 0.180

5 1.002 1.325 1.535 0.052 0.800 1.00 0.023 0.867 1.873 0.643

6 1.085 0.096 0.08 0.92 1.04 1.001 1.009 0.000 1.430 0.518

7 0.376 1.823 0.009 0.03 0.726 0.004 0.078 0.009 1.009 0.543

Table 6: Residual Energy(nJ) in each node of 8x10 Multiple Mobile Sink WSNs after 1646 iterations.

1 2 3 4 5 6 7 8 9 10

0 1.002 0.325 0.535 0.052 0.800 1.000 0.023 0.000 0.873 0.643

1 0.902 0.963 1.001 1.258 0.020 0.000 1.109 0.003 0.424 0.970

2 0.376 0.823 0.000 0.030 0.726 0.004 0.078 0.009 0.009 0.543

3 0.902 0.090 0.001 0.258 0.020 0.000 0.109 0.008 0.424 0.000

4 0.876 0.021 0.002 0.000 0.000 0.467 0.024 0.000 0.623 0.035

5 0.096 0.000 0.009 0.036 0.826 0.104 0.778 0.209 0.009 0.518

6 0.085 0.086 0.000 0.002 0.004 0.000 0.096 0.009 0.230 0.623

7 0.876 0.021 0.002 0.000 0.090 1.467 0.024 0.000 0.623 0.035

Table 7: Lifetime of the networks with Variable number of sensor nodes in a given area 100m x 100m.

Nodes 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80

SS 143 298 452 547 667 713 760 778 804 824 856 889 904 910 914

SMS 276 438 618 734 868 964 1048 1099 1167 1201 1248 1298 1333 1346 1386

MMSS 354 556 739 866 996 1090 1179 1239 1296 1352 1398 1469 1528 1589 1646

formly and thus improves the lifetime of the network.

The selection of optimal number of mobile sinks

depend on the size and density of the network. When

the number of mobile sink increases to three, the net-

work lifetime is approximately equals to lifetime of

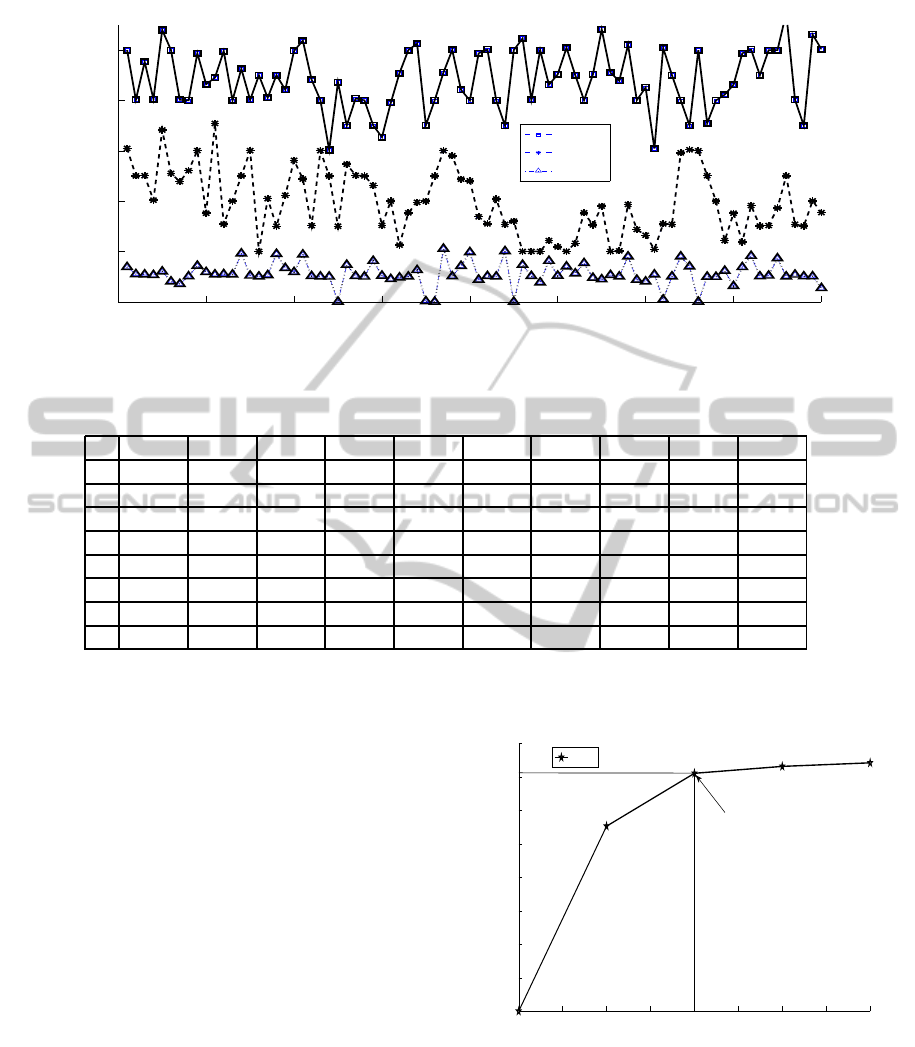
the network with two mobile sinks as shown in Figure

4. We can conclude that two mobile sinks are optimal

for the network with 80 nodes.

Figure 5 and 6 presence the lifetime of the MMSS,

SMS and SS. It is observed that the lifetime of MMSS

approach is higher than SMS and SS approaches.

While the lifetime of SS and SMS approach is 914

and 1386 time units, the lifetime of MMSS approach

is 1646 units i.e., 56% more than SS and 28% more

than SMS.

Figure 7 depicts the number of sinks required for

a variable number of sensors. It is observed that two

sinks are sufﬁcient for nearly 100 sensor nodes and

there after there is a linear increase in the requirement

of sinks to maintain the desired performance of life-

time and delay.

Figure 8 shows plot of the graph for the delay and

number of sensor nodes with static sink, single mo-

bile sink and multiple mobile sinks. The simulation

10 20 30 40 50 60 70 80

Number of Sensor Nodes

Network lifetime (weeks)

MMSS

SMS

Figure 5: Comparison of lifetime between the MMSS, SMS

and SS Networks.

starts with 10 sensor nodes to 80 nodes. Response

Time (delay) is calculated as per Equation 8. We ob-

serve that there is a considerable reduction in delay

for multiple mobile sink. This reduction of delay is

due to less number of hops and reduced distance be-

tween the source and the sink. In SS approach, the

average delay is 37 msec for 10 nodes while 30 msec

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND

LIFETIMEMAXIMIZATION INWIRELESS SENSOR NETWORKS

0 10 20 30 40 50 60 70 80

200

400

600

800

1000

1200

1400

1600

1800

Number of Sensor Nodes

Number of Iterations

MMSS

SMS

Figure 6: Comparison of number of iterations between the

MMSS, SMS and SS Networks.

0 50 100 150 200 250 300

0.5

1.5

2.5

3.5

Number of Sensor Nodes

Number of sinks

Figure 7: Number of nodes vs Number of sinks.

and 25msec respectively for SMS and MMSS ap-

proaches. Thus there is reduction in delay by 50% in

MMSS in comparison to SS. As the network density

increase, there is gradual reduction in average delay.

Though, there is large reduction in delay between SS

and SMS, but the reduction is much lower between

SMS and MMSS.

8 CONCLUSIONS

In WSN with a static sink, all source node forwards

data towards the sink. In a single mobile sink net-

work, sink moves to pre-determined positions and

stays for the sojourn time to collect the data. We

propose a distributed algorithm with Multiple Mobile

Synchronized Sink to improve the lifetime of the sen-

sor network. A linear program model is proposed to

increase the lifetime of the network and to reduce the

delay in the transmission of data between the source

10 20 30 40 50 60 70 80

Number of Sensor Nodes

Average Delay(msec)

SMS

MMSS

Figure 8: Number of nodes vs Response Time (Delay).

node and the mobile sink nodes. For the proposed

model, simulation is carried out for multiple mobile

sink which increases the lifetime by 56% over single

static sink and 28% over single mobile sink network.

During the last iteration of MMSS WSN, the residual

energy of all the sensor nodes is almost same which

shows that energy drains uniformly and thus increases

the lifetime of the network. The proposed MMSS al-

gorithm minimizes the delay in the network at a very

small increase in cost of multiple mobile sinks. In

future, this can be developed for large scale WSNs

including reliability and recovery.

REFERENCES

Chang, J. and Tassiulas, L. (2000). Energy conserving rout-

ing in wireless ad-hoc networks. In IEEE INFOCOM,

pages 22–31.

Gandham, S., Dawande, M., Prakash, R., and Venkatesan,

S. (2003). Energy efﬁcient schemes for wireless sen-

sor networks with multiple mobile base stations. In

IEEE GLOBECOM, volume 1, pages 377–381.

Gatzianas, M. and Georgiadis, L. (2008). A distributed al-

gorithm for maximum lifetime routing in sensor net-

works with mobile sink. In IEEE Transactions on

Wireless Communications, volume 7, pages 984–994.

Getsy, S. S., Kalaiarasi, R., Neelavathy, P. S., and Sridha-

ran, D. (November, 2010). Energy efﬁcient clustering

and routing in mobile wireless sensor network. In In-

ternational Journal of Wireless & Mobile Networks,

volume 2.

Kusy, B., Lee, H., Wicke, M., Milosavijevic, N., and

Guibas, L. (April 13-16, 2009). Predictive qos rout-

ing to mobile sinks in wireless sensor networks. In

Proceedings of ISPN.

Luo, J. (2006). Mobility in wireless networks: Friend or

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

foe, network design and control in the age of mobile

computing. In Ph.D. dissertation, EPFL,.

Luo, J., Panchard, J., Piorkowski, M., Grossglauser, M., and

Hubaux, J. P. (2005). Mobiroute: Routing towards a

mobile sink for improving lifetime in sensor networks.

In the National Conference Center in Research on Mo-

bile Information and Communication Systems(NCCR-

MICS).

Madan, R., Cui, S., Lall, S., and Goldsmith, A. (2005).

Cross-layer design for lifetime maximization in

interference-limited wireless sensor networks. In

IEEE INFOCOM, volume 3, pages 1964–1975.

Madan, R. and Lall, S. (2006). Distributed algorithms

for maximum lifetime routing in wireless sensor net-

works. In IEEE Transactions on Wireless Communi-

cations, volume 5, pages 2185–2193.

Michail, A. and Ephremides, A. (2003). Energy-efﬁcient

routing for connection oriented trafﬁc in wireless ad-

hoc networks. In Mobile Networks and Applications,

pages 517–533.

Weiwang, V. S. and Chua, K. C. (August 2005). Using mo-

bile relays to prolong the lifetime of wireless sensor

networks. In Proceeding of MOBICOM’05. Cologne,

Germany.

Xiao, L., Johansson, M., and Boyd, S. (2004). Simultane-

ous routing and resource allocation via dual decompo-

sition. In IEEE Transactions Community, volume 52,

pages 1136–1144.

Zhi, H., San-Yang, L., and Xiao-Gang, Q. (July 2010).

Overview of routing in dynamic wireless sensor net-

works. In International Journal of Digital Content

Technology and its Applications, volume 4.

MULTIPLE MOBILE SYNCHRONISED SINKS (MMSS) FOR ENERGY EFFICIENCY AND

LIFETIMEMAXIMIZATION INWIRELESS SENSOR NETWORKS