
CTG
E
: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE
GENERATION ALGORITHM FOR DETECTING REGRESSION
BUGS IN EVOLVING PROGRAMS
Anh D. Le, Tho T. Quan, Nguyen T. Huynh and Phung H. Nguyen
Faculty of Computer Science and Engineering, Hochiminh City University of Technology, Hochiminh City, Vietnam
Keywords: Constraint-based test-case generation, Regression bugs, Evolving programs debugging.
Abstract: In this paper, we investigate a kind of logic error occurring in evolving programs, known as regression bug.
This error reflects a practical situation that when a program or software is evolved to meet with new
requirements, it may accidentally violate the original requirements. Hence, the paper makes three theoretical
contributions. First, we show that the test-case generated by typical white-box approach are not sufficient to
cover all probable regression bugs. Next, we propose a new approach based on combined constraint to solve
this problem. Finally, we introduce an ultimate CTG
E
(Efficient Constraint-based Test-cases Generation)
algorithm whose complexity is reduced into linear time, thus becoming practical. The soundness of our
theoretical contribution is formally proved and supported by some initial experiments conducted in
education environment.
1 INTRODUCTION
Testing is the primary and common way to check the
correctness of software. Testing also incurs a
substantial cost in software development (Heumann,
2002). Among the various kinds of testing, unit
testing plays an important role in software quality,
since it helps detect errors in each individual
component’s logic.
Beside testing, the other main way to check
correctness of software is code inspection. Over last
few years, some automatic code-inspection tools are
built based on static analysis. These tools usually
generate an overly large number of warning and
even false alarms that do not actually correspond to
programming errors (false positive).
Thus, the most popular approach of software
testing today is still relying on test-case. Basically, a
test-case is a set of inputs, execution conditions and
desired outputs which can be tested by the system
when functioning accordingly using some test
procedures and test scripts.
However, the generation of test-case is usually
costly and thus requiring a systematic method.
White-box testing technique, based on flow-control
analysis, is typically applied in this case (Hutcheson,
2003). Alongside this approach, many attempts have
been made to automatically explore program paths
for test-case generation purpose (Cadar, Dunbar and
Engler, 2008; Godefroid, Klarlund and Sen, 2005).
Especially, the concolic testing, which is a hybrid
software verification technique that interleaves
concrete execution (testing on particular inputs) with
symbolic execution (Sen, Marinov and Agha, 2005),
has emerged recently as an efficient technique for
test-case generation. This technique is then adopted
and exploited remarkably in various testing tools
like PathCrawler (Williams, Marre, Mouy and
Roger, 2005), jCUTE (Sen and Agha, 2006) and
SAGE (Godefroid, 2007).
Nevertheless, when employed in real situations of
industry projects, the cost for exploring all of
possible paths is extremely expensive, because the
number of program path will increase exponentially
with the number of branch statements.
Dynamic slicing (Wang and Roychoudhury, 2008)
is the most practical technique to deal with this
limitation. This technique will slice the program
statements into a subset of program's execution trace
that only contains statements affecting a program's
output. Based on that, we can only generate one test
case for all of the paths that have the same output
effects, instead of generating unnecessarily multiple
test-cases for all of the paths.
This dynamic slicing technique is also very useful
36
Le A., Quan T., Huynh N. and Nguyen P..
CTGE: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE GENERATION ALGORITHM FOR DETECTING REGRESSION BUGS IN EVOLVING
PROGRAMS.
DOI: 10.5220/0003501400360043
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 36-43
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

when a program evolved, that is when a new version
of program is released with some substantial
changes made. Using slicing, one can recognize the
modified part in the new program, then generate
test-case that covers this modified path and analyze
the affected results to find program bugs (Qi,
Roychoudhury and Liang, 2010).
However, when a program is evolved into a new
version to meet new requirements or just to refine
the code, chances are that the new evolved program
may accidentally violate the original requirements.
This kind of errors, which is typically regarded as
regression bug, is occurring quite frequently in
practical situations of software development.
Unfortunately, the typical white-box testing is not
able to be fully detected this kind of error, even
when the flow analysis is performed on both original
and evolved versions. To make it clearer, in the
following discussion in Section 2, we will give some
motivating examples on this issue.
To overcome this problem, we suggest an
approach of using constraints combined from path
conditions of both original and evolved program
versions. We then formally prove the soundness of
this approach, under the context of well-conditioned
programs. To make this approach practical, we also
propose an algorithm, known as CTG
E
(Efficient
Constraint-based Test-case Generation) that reduces
the cost of test-case generation from exponential
complexity to linear one.
The rest of the paper is organized as follows.
Section 2 presents a motivating example which
shows that when a program evolves, neither test-
cases generated merely from the old version nor the
new version are sufficient to detect regression bug.
Section 3 discusses our proposed approach on
generating test-case by combining execution paths
from the previous version and the evolved version of
a program into constraints. In Section 4, we
introduce the ultimate CTG
E
algorithm, an
improvement of the test-case generation algorithm to
reduce its complexity significantly. Section 5 gives
some experiments and Section 6 concludes the
paper.
2 MOTIVATING EXAMPLE
To give a clear motivation of our work, we first
define well-conditioned program as follows.
Definition 1 (Well-conditioned Program).
A program P is said well-conditioned with respect to
a property π, denoted as ∠(P,π), if P produces same
outcomes w.r.t. π for all inputs satisfying same , path
conditions in P.
void f(int n){
if(n>0) return n = 2*n;
else return n = -2*n;
}
Listing 1: An example program P
X
.
Example 1. In the example program P
X
given in
Listing 1, there are two path conditions C
1
: (n >0)
and C
2
: (n ≤ 0) corresponding to the execution
paths of if and else clauses. Let us consider two
properties: (i) π
1:
the
program result is a positive
number; and (ii) π
2:
the
program result is an even
number. One can easily observe that all inputs
satisfying C
1
(e.g. n= 4) will make π
1
true. Similarly,
all inputs satisfying C
2
(e.g. n = -7) will make π
1
false. Thus, we can say P
E
is well-conditioned w.r.t.
π
1
or ∠(P
E
,π
1
). In contrast, all inputs satisfying C
1
or C
2
cannot guarantee the same outcomes w.r.t. π
2
.
For instance, the inputs of n=3 and n=4 both satisfy
C
1
but making π
2
false and true respectively.
In the situation of testing a program P against a
requirement R, it is easily observable that if ∠(P,R)
then a set of test-cases covering all of path
conditions in P is sufficient to detect any bugs if
occurring.
Example 2. (Requirement R
P
) Write a function f
taking an integer parameter n that returns the
absolute value of n.
For instance, let us consider the requirement R
P
given in Example 2. In Listing 2(a), an
implementation of f is given in program V
P,
which
has two path conditions P
1
= (n>0) and P
2
= ¬(n>0).
Since ∠(V
P
,R
P
), two test-cases covering those two
path conditions of V
P
, e.g. n=5 and n=-7, are
sufficient to ensure the correctness of V
P
.
1
int f(int n){
if(n>0) return n;
else return -n;
}
(a) The previous version Vp
int f(int n){
if(n>3)
{
Global++;
return n;
}
else return -n;
}
(b) The evolved version VE with regression bugs
Listing 2: Evolving programs.
1
In this paper we only discuss generating test-cases covering
all execution paths. The test-cases for extreme cases, for
example n=0 for the program in Listing 1(a
), are out of the
scope of this paper.
CTGE: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE GENERATION ALGORITHM FOR DETECTING
REGRESSION BUGS IN EVOLVING PROGRAMS
37

Example 3. (Requirement R
E
) Write a function f
taking an integer parameter n that returns the
absolute value of n. In addition, if n is greater than
3, f will increase the value of the global variable
Global by 1.
Assume that the requirement is now upgraded in
order to fulfill a new requirement R
E
as present in
Example 3. We say that R
E
is evolved from R
P
since
we can consider R
E
= R
P
∪R
N
, where R
N
is the
additional requirement of “if n is greater than 3, f
will increase the value of the global variable Global
by 1”. Then, V
P
is evolved accordingly as a new
version V
E
given in Listing 1(b).
Since ∠(V
E
,R
N
), two test-cases covering all two
path conditions Q
1
= n >3 and Q
2
= ¬(n>3) of V
E
,
e.g. n = 5 and n = -3, are sufficient to test whether V
E
Table 1: Constraints generated.
Conjunction Combined
Constraint
Simplified
Constraints
Test-
case
P
1
∧ Q
1
n>0 && n>3 n >3 n = 5
P
1
∧ Q
2
n>0&& !(n>3) 0 < n < 3 n = 2
P
2
∧ Q
1
!(n>0)&& n>3 no test-
case
P
2
∧ Q
2
!(n>0)&&
!(n>3)
n <=0 n = -7
fulfills the additional requirement R
N
. But those two
test-cases cannot show that V
E
violates the old
requirement R
P
. For example, if the input is 2, the
result will wrongly be -2. Generally, this problem
arises since we cannot always guarantee that
∠(V
E
,R
P
).
Note that even though this is only a toy problem,
the logic error in Listing 2(b) reflects a practical
situation occurring in evolving programs. That is,
while making the evolved program satisfy the
additional requirements, we may accidentally violate
the original requirements. We consider this kind of
error as regression bugs as introduced in Section 1.
The above-discussed examples also show that
even though employing test-case covering all path
conditions in both previous and evolved versions of
evolving programs, we can still miss the regression
bugs. In the next section, we will introduce the
combined constrain solving approach to deal with
this problem.
3 CONSTRAINT SOLVING
FOR REGRESSION BUGS
DETECTION
The motivating example in Section 2 has well
illustrated that when a program evolves from an old
version to a new evolved version, both path
conditions of two versions should be taken into
account when generating test-cases. The philosophy
here is that a program will be considered evolved
when new requirement is added, like stated in
Example 1 and Example 2. Thus, the new program
should satisfy not only new requirements added but
also old requirements as well.
In order to do this, we make usage of an approach
based on combined constraint as follows. From the
path conditions of both old and evolved versions, we
generate combined constraints by make conjunctions
of the path conditions. Each combined constraint is a
conjunction of a pair of path conditions, one from
the old version and the other from the evolved
version. Then, we generate test-cases that cover all
of possibly combined constraints. That is, we
generate some input values that satisfy the combined
constraints. The constraint solving here is by no
means an easy taught to be done manually. In
practice, we use the theorem prover Z3 (Bjørner and
Moura, 2009) to make the constraints simplified and
generate test-cases accordingly for each constraint
generated.
For instance, Table 1 presents the combined
constraints generated from programs in Listing 1 and
the test-cases generated accordingly. Obviously, we
can detect the regression bug when the test-case of n
= 2 is executed.
The algorithm CTG to generate test-case is
presented in Figure 1. In the algorithm, there is a
particular operation of solve_constraint included.
This operation is in charge of generating combined
constraints by conjunction and makes them
simplified, then finds an appropriate test-case
fulfilling the constraint. This operation is supposedly
handled by means of a theorem prover.
The CTG algorithm should be sufficient to find
any regression bugs. In Theorem 1, we show that
this statement is sound under Assumption 1.
Algorithm: CTG (Constraint-based Test-
cases Generation)
Input: V
P
,V
E
: Original and evolved
programs
Output: T : set of test-cases
Operations
T = Ø
Foreach (path condition α ∈ V
P
)
Foreach (path condition β ∈ V
E
)
t = solve_constraint (α∩β)
If t ≠ Ø then
Add t to T
Endif
End for
E
nd for
Figure 1: The CTG (Constraint-based Test-case
Generation) algorithm.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
38

Assumption 1. Given a previous version V
P
that
is well-conditioned w.r.t an original requirement R
P,
i.e.
∠
(V
P
,R
P
). When V
P
is evolved into a new
version V
E
to fulfil new requirement R
N
, then
∠
(V
E
,R
N
).
Theorem 1. The set of test-cases generated by
CTG algorithm is sufficient to detect regression bugs
on a program V
N
evolved from original program V
P
when the requirements evolved from R
P
to R
N
respectively.
Proof. If there is a regression bug ϑ occuring in
V
N
, then exists an input I that results in different
outcomes of O
P
and O
E
w.r.t. R
P
when executed in
V
P
and V
N
respectively. Assume that I belongs to
condition paths α∈V
P
and β∈V
N
respectively. Since
∠(V
P
,R
P
) and ∠(V
E
,R
N
) and R
P
⊂R
N
, any input
generated from the combined constraint α∩β will
result in the same outcome O
P
and O
E
w.r.t. R
P
when
executed in V
P
and V
N
respectively. Since I∈α and
I∈β then α ∩ β ≠∅, i.e. there is at least an input
I’∈α∩β existing and will be generated when the
CTG algorithm tries to make all posible
combinations of condition paths between V
P
and V
N,
thus causing the corresponding regression bug ϑ to
be detected accordingly
.
Complexity Analysis. It is easily observable that
the CTG algorithm produces test-cases by solving of
possible constraints generated from the old version
V
P
and the evolved version V
E
. Thus, it suffers high
complexity as it takes Ο(N×M) times to make a
solver process all constraints where N and M are the
path conditions on V
P
and V
E
respectively. In the
next section, we introduce the CTG
E
algorithm, an
enhanced algorithm that only involves solver to
process solvable constraints, thus improving
significantly the performance of test-case generation
process.
4 THE CTG
E
ALGORITHM
Among the 4 constraints presented in Table 1, there
are 3 solvable constraints and one unsolvable one
(i.e. a constraint that we cannot find any test-
case/input satisfying it). However, the CTG
algorithm requires a solver to process unnecessarily
all of 4 constraints. To overcome this problem, in the
new version of CTG
E
algorithm presented in this
section, we will take into account only solvable
constraints. The CTG
E
algorithm is shown in
Figure 2.
Algorithm: CTG
E
(Efficient Constraint-
based Test-cases Generation)
Input: V
P
,V
E
: Original and evolved
programs
Output: T : set of test-cases
Operations
T = Ø
C
mark
= Ø
Foreach (path condition χ ∈ V
P
)
t = solve_constraint (χ∩
¬C
mark
)
combine(t)
End For
SubProcedure combine (test-case t)
Begin
add t to T
α = symbolic_exec(t,V
p
)
β = symbolic_exec(t,V
E
)
C
mark
= C
mark
∪ (α ∩ β)
if (
α∩¬β∩¬C
mark
) ≠∅ then
combine(solve_constraint(
α∩¬β∩¬C
mark
))
end if
if (
¬α∩β∩C
mark
) ≠∅ then
combine(solve_constraint(
¬α∩β∩C
mark
))
end if
E
n
d
Figure 2: Efficient Constraint-based Test-case Generation
(CTG
E
) algorithm.
The major improvement of CTG
E
is that it does
not try to make all possible combined constraints.
Instead, CTG
E
processes each path condition of the
original version V
P
. For each path condition, CTG
E
first produces an appropriate test-case. Then, it calls
a subprocedure named combine to further process.
For every test-case t processed in combine, a
specific function named symbolic_exec will be
called to find the corresponding path conditions of t
when executed in V
P
and V
E
respectively. The
operation of symbolic_exec will perform symbolic
execution, a classical technique to trace the
execution path of given input by tracking symbolic
rather than actual values (King, 1976). Based on the
retrieved path conditions, combine keeps generating
relevant constraints and calls itself recursively to
generate more suitable test-cases. During the whole
process of CTG
E
, we also make use of a special
constraint named C
mark
which marks the explored
parts in the space of test-case domain. Therefore,
CTG
E
can avoid duplication when generating
constraints and test-cases.
Theorem 2. The set of test-cases generated by
CTG
E
algorithm is sufficient to detect regression
bugs on a program V
N
evolved from old program V
P
when the requirements evolve from R
P
to R
N
respectively.
Proof. We consider an undirected graph G = <V,E>
constructed as follows. Each vertex v in V
corresponds to a solvable combined constraint
generated by the CTE algorithm. We add an edge
CTGE: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE GENERATION ALGORITHM FOR DETECTING
REGRESSION BUGS IN EVOLVING PROGRAMS
39

Figure 3: A graph representation of combined constraints.
e
ij
= (v
i
,v
j
) to E if v
i
and v
j
are subcondition of a path
condition in either V
P
or V
N
.
For example, in Figure 3 is the graph constructed
when we consider the program versions presented in
Figure 1 and the combined constraints in Table 1. In
the graph, there are three vertices corresponding to
three solvable constraints in Table 1. There is an
edge connecting v
1
and v
2
since their constraints are
both subconditions of P
1
. Similarly, v
2
and v
3
are
connected since their constraints are both
subconditions of Q
2
Next, we relate the test-case generation process in
the CTG
E
as graph traversal carried out in G. A
vertex v is considered visited if CTG
E
produces a
test-case satisfying the corresponding combined
constraint of v. According to Theorem 1, if all
vertices in G are visited after CTG
E
finishes, then
CTG
E
generates sufficient test-cases to detect any
regression bugs.
When CTG
E
begins, it starts by a certain test-case
I generated to satisfy a path condition α of V
P
. Using
symbolic execution, one can determine the path
condition β of V
N
which I belongs to. It means that a
vertex q = α∩β just has been initially visited.
Consider the formula α∩¬β referring to a vertex
q’, which should be connected to q since α∩β and
α∩¬β are both subcondition of α. Let C
mark
be the
formula representing all of vertices already visited
(i.e. the combined constraints whose corresponding
test-cases have been generated already). Similarly
reasoning, we finally obtain that the two formulas
α∩¬β∩¬C
mark
and ¬α∩β∩¬C
mark
should represent
all vertices connecting to q which have not been
visited. By recursively solving those formulas and
updating C
mark
in the subprocedure combine, CTG
E
will iteratively visit all of vertices in the connected
component which q belongs to.
Lastly, one can note that by checking all of path
conditions of V
P
, CTG
E
will travel to all possible
connected components of G. Thus, all vertices of G
will be logically visited when CTG
E
performed and
there are no vertices doubly visited.
For instance, consider using CTG
E
for generating
test-case for evolving programs in Listing 1. Firstly,
the two path conditions P
1
and P
2
are collected.
Then, CTG
E
generates randomly a test-case for a
path condition. Let it be n = 4 for P
1
. Performing
symbolic execution on the test-case, one can realize
that the test-case falls into the combined constraint
P
1
∧Q
1
= n>0 && n>3 = n >3. Then, CTG
E
tries to
solve the formula P
1
∧¬Q
1
∧¬C
mark
with C
mark
being
updated as C
mark
=P
1
∧Q
1
. We have P
1
∧¬Q
1
∧¬C
mark
= n>0 && ¬(n>3) && ¬(n>3) = n>0 && n≤3.
Then, a test-case is generated accordingly, e.g. n = 2.
Next, combine (2) is invoked, which is
corresponding to the constraint P
1
∧Q
2
with C
mark
being updated as n > 3 ∪ n>0 && n ≤3 = n> 0. We
then have P
1
∧¬Q
2
∧¬C
mark
= n>0 && n>3 &&
!(n>0) = ∅, then then this formula is not considered.
Meanwhile, we have ¬P
1
∧Q
2
∧¬C
mark
= !(n>0)
&& !(n>3) && !(n>0) = n≤0. Solving this
constraint, we, for instance, get a new test-case of n
= -7. Then, combine(-7) is invoked accordingly. At
the moment, C
mark
is updated as n > 0 ∪ !(n>0) &&
!(n>3) = n > 0 ∪ n ≤ 0, making P
2
∧¬Q
2
∧¬C
mark
=
¬P
2
∧Q
2
∧¬C
mark
=¬P
1
∧Q
1
∧¬C
mark
= ∅. Thus, the
algorithm stops with no more test-cases generated.
Complexity Analysis. Performing elementary
analysis on CTG
E
, one can realize that CTG
E
will
involve the embedded solver 2K times, with K is the
number of test-cases generated and K ≤ N+M where
N and M are the path conditions on V
P
and V
E
respectively. If we take into account the actions of
generating N path conditions on V
P
, the total
complexity of CTG
E
will be Ο(2K +M) ~ Ο(3N +M)
which should be improved significantly compared to
that of the original CTG.
To illustrate this, consider the two versions of
evolving programs given in Listing 3. The program
intends to grade students’ works. After the
preliminary version is finished as presented in
Listing 3(a), a new version is released afterward as
presented in Listing 3(b).
int grade(int n){
if(n > 100) return Invalid;
else if(n>=90) return Excellent;
else if(n>=80) return Very good;
else if(n>=70) return Good;
else if(n>=60) return Fairly good;
else if(n>=50) return Average;
else if(n>=0) return Fail;
else return Invalid;
}
(a) Student grading program – preliminary version
int grade(int n){
if(n > 100) return Invalid;
else if(n>90) return Excellent;
else if(n>80) return Very good;
else if(n>70) return Good;
else if(n>60) return Fairly good;
else if(n>50) return Average;
else if(n>0) return Fail;
else return Invalid;
}
(b) Student grading program – final version
Listing 3: Evolving programs.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
40

There are 8 path conditions in each version,
therefore the CTG algorithm will make use of the
solver 64 times to generate test-cases. Meanwhile,
when CTG
E
is performed, it will basically generate 8
initial test-cases covering 8 path conditions of the
preliminary program as presented in Table 2 (the
test-cases presented here are just of example basis).
Table 2: Initial example test-cases for preliminary version
in Listing 2.
Condition Test case
n>100 103
n>=90 && n<=100 91
n>=80 && n<90 85
n>=70 && n<80 73
n>=60 && n<70 66
n>=50 && n<60 54
n>=0 && n<50 32
n<0 -7
Table 3: Total test-cases generated for evolving versions
in Listing 2.
Test
case
α
β
α∩¬β ¬α∩β
103 n>100 n>100 ∅ ∅
91
n>=90
&&
n<=100
n>90
&&
n<=100
new test-
case: 90
∅
90
n>=90
&&
n<=100
n>80
&& n
<=90
∅ ∅
85
n>=80
&& n<90
n>80
&&
n<=90
new test-
case: 80
∅
80
n>=80
&& n<90
n>70
&&
n<=80
∅ ∅
73
n>=70
&& n<80
n>70
&&
n<80
new test-
case: 70
∅
70
n>=70
&& n<80
n>60
&&
n<=70
∅ ∅
66
n>=60
&& n<70
n>60
&&
n<=70
new test-
case: 60
∅
60
n>=60
&& n<70
n>50
&&
n<=60
∅ ∅
54
n>=50
&& n<60
n>50
&&
n<=60
new test-
case: 50
∅
50
n>=50
&& n<60
n>0 &&
n<=50
∅ ∅
32
n>=0 &&
n<50
n>0 &&
n<=50
new test-
case: 0
∅
0
n>=0 &&
n<50
n<=0 ∅ ∅
-7 n<0
n<=
0
∅ ∅
Then, when the algorithm advances, there will be 6
additional test-cases generated corresponding to
non-empty domain marked in Table 3. Totally, the
solver only needs to be involved 14 times for
generating test-cases and 8 times for initial path
conditions.
Table 4: Programming problems used as experimental data.
No Problem Constraint
Solver
calls
(CTG)
Solver
calls
(CTG
E
)
1
Leap year
checking
14 42 40
2
Triangle
classification
22 89 31
3
Date validation
checking
62 736 90
4
Time
validation
checking
28 96 37
5
Factorial
computing
28 96 58
6 Calculating x
y
28 96 56
7
Prime number
checking
56 384 92
8 Sum of 1..n 25 84 54
Table 5: Bugs detected by white-box and combined
constraints approach.
Problem
No
Real Bugs
Detected by
white-box
Detected by
CTG
(E)
1 12 11 12
2 10 6 10
3
4
5
6
7
8
12
13
14
11
12
12
10
10
14
11
12
12
10
13
13
11
12
11
Total
96 86(89%) 94(98%)
5 EXPERIMENTAL RESULTS
In order to evaluate the performance of the CTG
E
algorithm, we have conducted an experiment in the
education domain. The requirements to be fulfilled
in this experiment are non-trivial programming
problems given to students. The list of problems is
given in Table 4, which also gives the information of
the combined constraints make from path conditions.
For loop-based programs, the path conditions are
computed using the coverage analysis technique
(Spillner, Linz and Schaefer, 2006), in which the
loops are enforced to repeat respectively 0,1,2 and
more than 2 times. Thus, our algorithm may have
some limitations on programs with complicated
loops.
The dataset used in this experiment is collected
CTGE: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE GENERATION ALGORITHM FOR DETECTING
REGRESSION BUGS IN EVOLVING PROGRAMS
41
from the work of 50 students. In fact, there are
actual marked programming works. Basically, for
each programming problem, the teacher will produce
a sample solution. In order to mark student works
automatically, some test-cases are generated for
testing. However, as discussed in Section 2, if we
apply the typical white-box approach for generating
test-cases, the test-cases are not sufficient to detect
all of bugs in student works, even though both
sample solutions and actual students’ works are
concerned when test-cases are generated.
When manually inspecting, we observe that there
are only 89% students’ bugs detected using white-
box approach. Exact information on improvement of
bug detection is given in Table 5. When the
constraint-based approach is applied with teachers’
sample solutions playing the roles of original
versions and student works evolved versions, the
performance of bug detection is significantly
improve with 98% bugs detected. Few bugs are still
missed because the Z3 solver fails to resolve some
complex non-linear expression in path conditions.
We have also compared the performance of the
CTG and CTG
E
algorithms in terms of execution
time. In Table 4, we can observe that the number of
solver call is significantly reduced in CTG
E
. As a
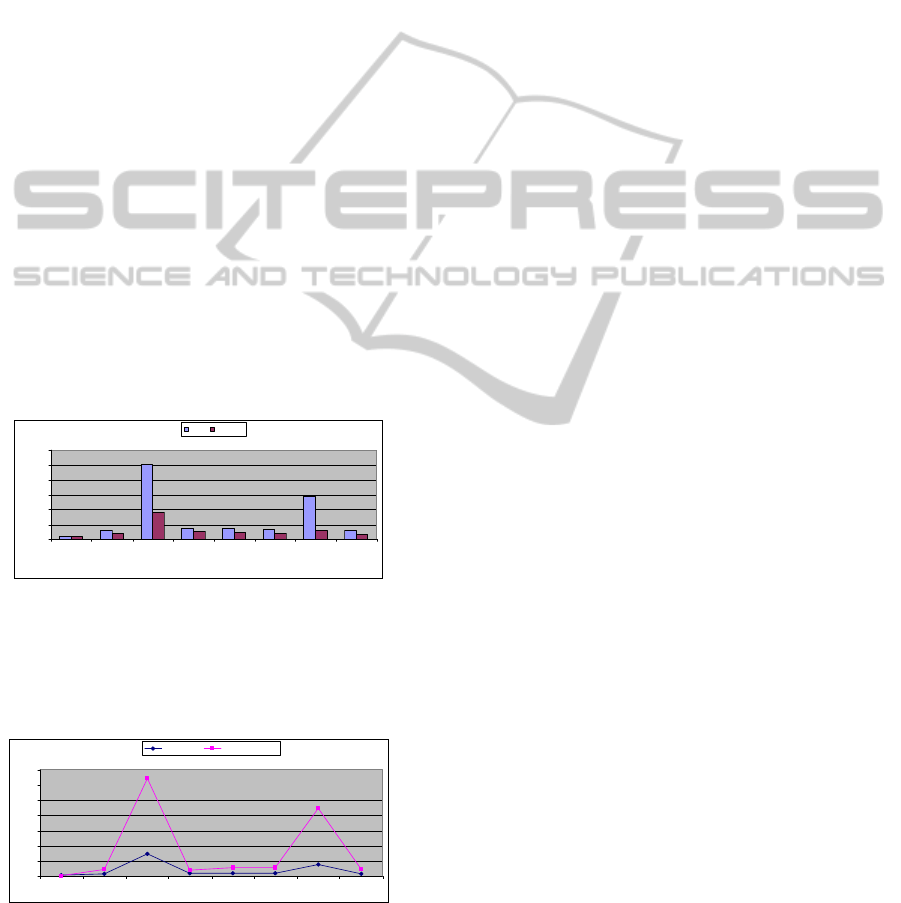
result, the execution time is improved remarkably, as
seen in Figure 4.
0
10
20
30
40
50
60
12345678
Problem
Time (seconds)
CTG CTG(E)
Figure 4: Improvement of time execution achieved by
CTG
E
.
Moreover, Figure 5 also shows that when the more
number of constraints increases, the higher
improvement on execution time achieved.
0
500
1000
1500
2000
2500
3000
3500
12345678
Constraint Time difference
Figure 5: Comparison on execution time difference
between CTG and CTG
E
w.r.t. numbers of combined
constraints.
6 CONCLUSIONS
White-box testing is an effective technique for bug
detection. However, in case of evolving program,
this technique is not sufficient to deal with
regression bugs, occurring when an evolved version
violates original requirement already fulfilled by the
previous versions.
In this paper, we first explain by a means of
motivation example why white-box testing may fail
to discover regression bugs. Then, we introduce a
combined constraint-based approach to theoretically
solve the problem, with formal definitions and proof
provided. To avoid the explosion path problem, we
refine the approach as ultimate algorithm known as
CTG
E
whose complexity is reduced significantly to
linear time.
We have also preliminary tested our approach in
education environment, with dataset being
programming works collected from students. The
experimental results showed that the CTG
E
algorithm achieved better performance in terms of
bug detection coverage and execution time,
compared to the white-box testing. It also shows
potential to apply CTG
E
to
industry environment.
ACKNOWLEDGEMENTS
This work is part of the Higher Education Project 2
project (supported by World Bank and Hochiminh –
Vietnam National University).
REFERENCES
Bjørner, N. and Moura, L. D. (2009). Z3^10: Applications,
Enablers, Challenges and Directions. In Proceedings
of Workshop on Constraints in Formal Verification.
Cadar, C., Dunbar, D. and Engler, D. R. (2008). Klee:
Unassisted and automatic generation of high-coverage
tests for complex systems programs. USENIX
Symposium on Operating Systems Design and
Implementations.
Godefroid, P., Klarlund, N. and Sen, K. (2005). DART:
Directed automated random testing. ACM Publisher,
In Proceedings of the 2005 ACM SIGPLAN
conference on Programming language design and
implementation, 40(6), 213-223. doi:10.1145/
1065010.1065036
Godefroid, P. (2007). Random testing for security:
blackbox vs. whitebox fuzzing. ACM Publisher, In
Proceedings of the 2nd international workshop on
Random testing: co-located with the 22nd IEEE/ACM
International Conference on Automated Software
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
42

Engineering, 1-1. doi:10.1145/1292414.1292416
Heumann, J. (2002). Generating Test Cases from Use
Cases. Journal of Software Testing Professionals,
3(2).
Hutcheson, M. L. (2003). Software Testing Fundamentals-
Methods and Metrics, Wiley Publishing.
King, J. C. (1976, July). Symbolic execution and program
testing. Communications of the ACM, 19(7), 385-394.
doi:10.1145/360248.360252
Qi, D., Roychoudhury, A. and Liang, Z. (2010). Test
generation to expose changes in evolving programs.
ACM Publisher, In Proceedings of the IEEE/ACM
international conference on Automated software
engineering, 397-406. doi:10.1145/1858996.1859083
Sen, K., Marinov, D. and Agha, G. (2005). CUTE: a
concolic unit testing engine for C. ACM Publisher, In
Proceedings of the 10th European software
engineering conference held jointly with 13th ACM
SIGSOFT international symposium on Foundations of
software engineering, 30(5), 263-272.
doi:10.1145/1081706.1081750
Sen, K. and Agha, G. (2006). CUTE and jCUTE :
Concolic Unit Testing and Explicit Path Model-
Checking Tools. Springer-Verlag, Computer Aided
Verification: In Proceedings of the 18th International
Conference, 4144, 419-423. doi:10.1007/11817963_38
Spillner, A., Linz, T. and Schaefer, H. (2006). Software
Testing Foundations. California: Rocky Nook.
Wang, T. and Roychoudhury, A. (2008). Dynamic slicing
on java bytecode traces. ACM Publisher, ACM
Transactions on Programming Languages and
Systems, 30(2). doi:10.1145/1330017.1330021
Williams, N., Marre, B., Mouy, P. and Roger, M. (2005).
PathCrawler: Automatic Generation of Path Tests by
Combining Static and Dynamic Analysis. Springer-
Verlag, Dependable Computing: In Proceedings of the
5th European Dependable Computing Conference,
3463, 281–292. doi:10.1007/11408901_21
CTGE: AN EFFECTIVE CONSTRAINT-BASED TEST-CASE GENERATION ALGORITHM FOR DETECTING
REGRESSION BUGS IN EVOLVING PROGRAMS
43
