
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS
WITH UML AND MARTE
Antonio García-Domínguez, Inmaculada Medina-Bulo
Department of Computer Languages and Systems, University of Cádiz, Cádiz, Spain
Mariano Marcos-Bárcena
Department of Mechanical Engineering and Industrial Design, University of Cádiz, Cádiz, Spain
Keywords:
Model-driven engineering, Performance testing, UML, MARTE, Non-functional requirements.
Abstract:
High-quality software needs to meet both functional and non-functional requirements. In some cases, soft-
ware must accomplish specific performance requirements, but most of the time, only high-level performance
requirements are available: it is up to the developer to decide what performance should be expected from each
part of the system. In this context, the MARTE profile was proposed by the OMG to extend UML for model-
driven development of real-time and embedded systems, focusing on assisting early performance analysis and
scheduling. We propose using the MARTE profile to derive the performance requirements of each action in
an UML activity diagram from the requirements of the containing activity and some local annotations. In
this work, we show how the MARTE profile can be used for this purpose, define algorithms for computing
the required throughput and time limit for each action and study their theoretical and empirical performance.
The algorithms have been integrated into the Papyrus UML diagram editor and feed back their results into the
original model. Running both algorithms on activities with 2
25
paths requires 10 seconds on average.
1 INTRODUCTION
In addition to functional requirements, software must
meet non-functionalrequirements. Among them, per-
formance plays a major role in shaping the user ex-
perience. In some cases, meeting specific perfor-
mance requirements is critical. This is the case not
only in soft and hard real-time systems, but also in
service-oriented architectures (Erl, 2008), where Ser-
vice Level Agreements (SLAs) may have been signed
between the provider and the consumer of a service.
For these reasons, there has been considerable
work in estimating and measuring the performance of
software systems (Woodside et al., 2007). Estimat-
ing the performance of a prospective system usually
requires building high-level execution and architec-
ture models and deriving a formalism from them, as
in (Smith and Williams, 2003; Woodside et al., 2005),
among many others. Measuring the performance of a
system requires instrumenting it to produce the de-
sired results, instead of building a model. These ap-
proaches complement each other: estimations can be
performed early, before the actual system is imple-
mented, while measurements are more accurate.
Measuring the performance of a system can be
useful for many purposes: finding performancedegra-
dations over time, identifying load patterns over spe-
cific time periods and checking if the system is meet-
ing its performance requirements. Obviously, this
last use case requires that the performance require-
ments have been previously defined. However, most
of the time, detailed performance requirements are
not provided (Weyuker and Vokolos, 2000). Devel-
opers may have to meet high-level performance re-
quirements without a clear view of what performance
is required in each part of the system.
In this work we propose a model-driven approach
to deriving the low-level performance requirements of
a system from high-level performance requirements.
The user creates UML models annotated with a small
subset of the MARTE profile (OMG, 2009) and runs
our inference algorithms to derive the low-level re-
quirements, feeding them back into the model.
The rest of this paper is structured as follows: in
Section 2, we introduce the MARTE profile for UML,
describe the subset used in our work and show our
54
García-Domínguez A., Medina-Bulo I. and Marcos-Bárcena M..
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE.
DOI: 10.5220/0003506000540063
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 54-63
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

running example. Section 3 defines the inference al-
gorithms and outlines some of the optimisations per-
formed. Section 4 is dedicated to analysing the re-
strictions imposed upon the algorithms and evaluating
their performance. Section 5 discusses related work.
Finally, Section 6 condenses the main points of this
paper and lists our future lines of work.
2 THE MARTE PROFILE
UML has been widely adopted as a general purpose
modelling language for describing software systems.
However, UML itself does not include support for
modelling scheduling, performance or time aspects,
among other non-functional aspects.
For this reason, the Object Management Group
proposed in 2005 the SPT (Schedulability, Performa-
bility and Time) profile (OMG, 2005), which ex-
tended UML with a set of stereotypes describing sce-
narios that various analysis techniques could take as
inputs. In 2008, OMG proposed the QoS/FT (Qual-
ity of Service and Fault Tolerance Characteristics and
Mechanisms) profile (OMG, 2008), with a broader
scope than SPT and a more flexible approach: users
formally defined their own quality of service vocabu-
laries and used them to annotate their models.
When UML 2.0 was published, OMG saw the
need to update the SPT profile and harmonise it with
other new concepts. This resulted in the MARTE
(Modelling and Analysis of Real-Time and Embed-
ded Systems) profile (OMG, 2009), published in
2009. Like the QoS/FT profile, the MARTE profile
defines a general framework for describing quality of
service aspects. The MARTE profile uses this frame-
work to define a set of pre-made UML stereotypes, as
those in the SPT profile.
In this section, we will introduce the parts of the
MARTE profile required for our algorithms and show
an example model, using its predefined stereotypes.
2.1 Selected Subset
The MARTE specification provides support for
model-based analysis and design of real-time and em-
bedded systems. Among its sub-profiles, we are in-
terested in the GQAM (Generic Quantitative Analy-
sis Modelling) profile. The GQAM domain model
describes the concepts of the GQAM profile using
the generic non-functional property modelling frame-
work in MARTE.
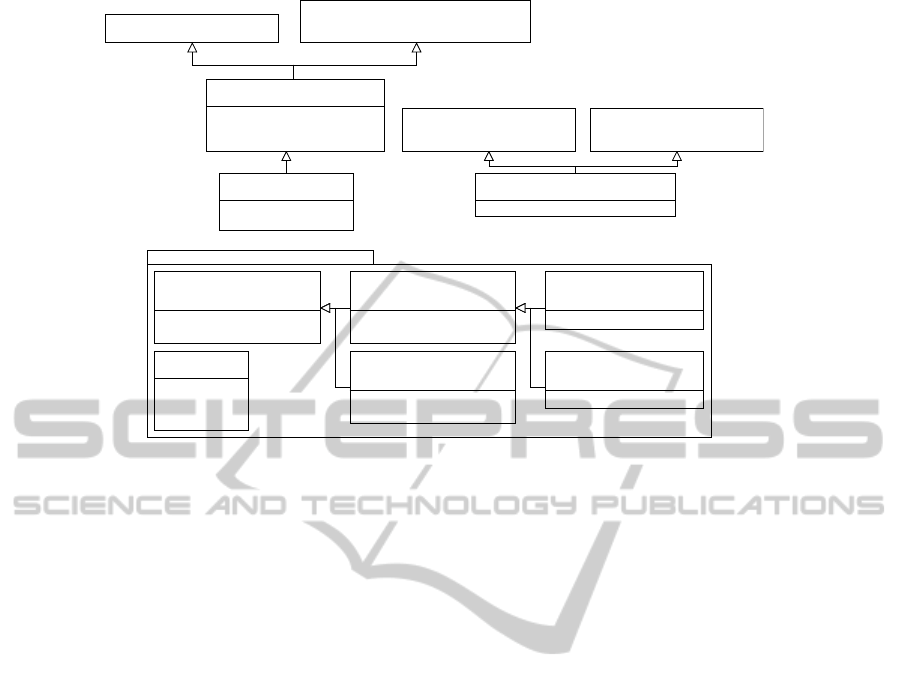
Figure 1 shows an UML class diagram with the
subset of MARTE used by our inference algorithms.
The stereotypes from the GQAM profile are pre-
fixed with “Ga” (standing for “generic analysis”), and
the non-functional property types from the normative
MARTE model library are prefixed with “NFP”. For
the sake of brevity, unused attributes have been omit-
ted. The stereotype and attributes used are:
«GaScenario»
• hostDemand: zero or more requirements on the
CPU time required.
• throughput: zero or more requirements on the
requests which should be handled per second.
• respT: zero or more requirements on the maxi-
mum response time when handling throughput
requests per second.
«GaStep»
• prob: probability of traversing a control flow.
• rep: number of times the activity is repeated.
«GaAnalysisContext»
contextParams contains a list of context param-
eters. These are variables which can be used
to parametrise the annotations using VSL (Value
Specification Language) expressions. VSL is a
textual language defined in MARTE.
All the non-functional property types in the nor-
mative MARTE library share several traits, as they
inherit from NFP_CommonType. Values can be speci-
fied as literals in the value attribute, or as VSL expres-
sions in the expr attribute. The source of a require-
ment (estimated, measured, calculated or required) is
described by the source attribute.
NFP_CommonType is a VSL tuple type.
In this paper we will use the notation
(key1=value1,...,keyN=valueN)
for VSL
tuples. For instance, a NFP_Duration of 5 mil-
liseconds required by the client is written as
(value=5, unit=ms, source=req)
.
2.2 Usage
In the previous section, we listed the elements of
MARTE used by our inference algorithms. In this
section, we will describe how they are to be used.
Activities must have the «GaScenario» and «Ga-
AnalysisContext» stereotypes. «GaScenario» indi-
cates the expected response time (respT) and through-
put (throughput) for the entire activity. «GaAnaly-
sisContext» only lists the context parameters (con-
textParams) which represent the slack per unit of
weight assigned to each action in the activity.
Control flows leaving decision nodes are anno-
tated with the «GaStep» stereotype, specifying the
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE
55
!"#
$ % !"#
!"#
&'()*+,-
.$
'
$'$
/01&(12
3
1451
6
/0 &( 2
.6
/07' &( 2
'
7' '
5&8
/0 &( 2
%
% .6
6
'
%
'31
1$!"#
451
131
3'
39$
/07' &( 2
$
7' $
'()*+,-
Figure 1: Class diagram of the subset of MARTE used by our algorithms.
probability (prob) of traversing one of the conditional
branches. The probabilities are estimated by the user.
Actions are annotated with the «GaStep» stereo-
type as well. The user must indicate their expected
number of repetitions (rep) and how the available
time is to be distributed among them. hostDemand
must contain a tuple with a VSL expression matching
M+W*swI
: M ≥ 0 is its minimum time limit, W ≥ 0 is
its weight and
swI
is its context parameter. The time
limit inference algorithm will set
swI
to the slack per
unit of weight assigned to that action.
After the algorithms are done, results are fed back
into the activity diagram, replacing those from previ-
ous runs. Actions are annotated with the inferred time
limits in hostDemand, and with the inferred through-
puts in throughput. Context parameters are set to the
slack per unit of weight assigned to their actions.
2.3 Running Example
Figure 2 shows the UML activity diagram which we
will use as running example for the rest of this paper.
Its activity, “Handle Order”, describes how to process
a specific order. Starting from the initial node:
1. The order is evaluated.
2. If rejected, close the order: we are done.
3. If accepted, fork into two execution branches:
(a) Create the shipping order and send it to the
shipping partner.
(b) Create the invoice, send it to the customer and
receive the payment.
4. Once these two branches are done, close the order.
According to the MARTE annotations, the activ-
ity should complete its execution in one second when
receiving one request per second. Most of the actions
have no minimum time limit and weight equal to 1,
except for “Evaluate Order”, whose CPU time is fixed
by the modeller to 0.4 seconds. All actions are run
once, to simplify the discussion. The user has esti-
mated that 80% of all orders are accepted.
3 INFERENCE ALGORITHMS
In the previous section, we explained how we used the
MARTE profile for our algorithms and described the
running example for this paper (Figure 2). In this sec-
tion we will outline the algorithms themselves. The
first algorithm computes the expected throughput of
each action, and the second algorithm computes the
time limit for each action. They improve upon those
in (García-Domínguez et al., 2010).
Both require that activities do not contain cycles,
that they only have one initial node, and that all their
actions are reachable from it. Let us define some
terms:
• s(e) and g(e) are the source and target vertex of
the edge e, respectively.
• i(n) and o(n) are the incoming and outgoing edges
of the node n, respectively.
• L > 0 is the expected response time (the global
time limit) of the selected activity, in seconds.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
56

!
"#$%%&'()*+()$,()&&()+()$+
-+-
.'-
%/01)*+
*+-
.'-
%01)$,
$,
.'-
%01)&&
&2'&#'
.'-
%01)+
+-
.'-
%01)$+
$+-
345-6
37
58-6
Figure 2: Example of usage of the MARTE profile for our algorithms.
• c(n) = (m(n),w(n)) ∈ C(L) is the constraint of
the node n, where m(n) is the minimum time limit
of n and w(n) is its weight (see Section 2.2). The
set of all valid constraints with L as global time
limit is C(L) = {(m,w)|0 ≤ m ≤ L,w ≥ 0}.
• Each path p also has a constraint, c(p) =
(m(p), w(p)) ∈ C(L), with m(p) =
∑
n∈p
m(n) and
w(p) =
∑
n∈p
w(n).
• A node n is run R(n) ≥ 1 times (once by default).
3.1 Throughput Inference
We will define T as a function which takes a node
or edge and produces its expected throughput. For a
control flow e, T(e) = P(e)T(s(e)), where P(e) is the
probability of traversing e.
For a node n, the actual formula depends on
its type. For an initial node, T(n) is the expected
throughput of the activity. For a join node, T(n) =
min
e∈i(n)
T(e), since requests in the least perform-
ing branch set the pace. For a merge node, T(n) =
∑
e∈i(n)
T(e), as requests from mutually exclusive
branches are reunited. For any other type of node,
T(n) = T(e
1
), where e
1
∈ i(n) is its only incoming
edge.
Using these formulas, computing
T(Create Invoice) for the example shown in Figure 2
requires walking back to the initial node, finding
an edge with a probability of 0.8, no merge nodes
and an initial node receiving 1 request per second.
Therefore, T(Create Invoice) = pL = 0.8.
To compute these values efficiently, the ex-
pressions are evaluated in a topological traver-
sal of the graph. For each action a, through-
put will contain a single tuple of the form
(value=T(a),unit=Hz,source=calc)
.
3.2 Time Limit Inference
Inferring the time limits of each action inside an activ-
ity is considerably more complex than inferring their
required throughputs. After more definitions, we will
describe the algorithm and some key optimisations,
and then apply it to the running example in Figure 2.
3.2.1 Preliminaries
The algorithm adds a tuple of the form
(value=t(n), unit=s, source=calc)
to the
attribute hostDemand of each action node n, where
t(n) is its inferred time limit. The algorithm also
updates the appropriate context parameter with the
final slack per unit of weight distributed to n.
Let I be the initial node of the activity being anno-
tated and let P
S
(n) contain all paths from the node n to
a final node. t(n) must meet the following constraints:
• For every action n, t(n) ≥ m(n): the assigned time
limit must be greater or equal than the minimum
set by the user.
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE
57

• For every path p in P
S
(I),
∑
n∈p
R(n)t(n) ≤ L: the
sums of the time limits over each path meet the
global time limit.
The available time “flows” from the initial node.
If a node n receives 0 ≤ r(n) ≤ L seconds, every path
p ∈ P
S
(n) receives r(p) = r(n) seconds to distribute
among its nodes. r(n) is not known a priori except
for the initial node: r(I) = L.
If the «GaStep» and «GaScenario» annotations are
consistent with eachother, then r(p) ≥ m(p) for every
path p: the minimum time constraints of all actions
are always met. s(p) = r(p) − m(p) ≥ 0 is known
as the slack of the path p. s(p) is distributed over
p according to the weight of each node: the slack
per unit of weight initially assigned to each node is
S
w
(p) = s(p)/w(p). When w(p) = 0, we assume that
S
w
(p) = 0: all nodes in p have a zero weight, so no
slack can be distributed.
The algorithms must ensure that w(p) > 0 ⇒
s(p) > 0, so every path p with a non-zero weight has
some slack to distribute. If this condition is not met
or the annotations are inconsistent, the user should be
notified and any change should be rolled back.
3.2.2 Definition
The algorithm is a recursive function which takes a
node n and the time it receives, r(n). Initially, n = I
and r(n) = L, the global time limit. The algorithm
follows these steps:
1. Select two paths from P
S
(n):
• p
ms
(n) has the minimum S
W
(p) when r(n) sec-
onds are available. In case of a tie, pick the path
with the maximum w(p).
• p
Mm
(n) has the maximum m(p).
2. If s(p
Mm
(n)) < 0, the minimum time limits cannot
be satisfied: abort.
3. If s(p
ms
(n)) = 0 and w(p
ms
(n)) > 0, there is no
slack in a path with a non-zero weight: abort.
4. Set the time limit of n, t(n), to m(n) +
S
w
(p
ms
(n))w(n). The remaining time will be T
R
=
T − R(n)t(n) seconds. Mark v as visited.
5. Sort each edge e ∈ o(n) in ascending order of
S
w
(p
ms
(g(e))) with r(g(e)) = T
R
, the minimum
slack per unit of weight when T
R
seconds are
available for all paths that start at the target of e.
6. Visit each edge in o(n):
(a) If the target of e has been visited before, check
if the time which was sent to it, T
′
R
, is strictly
less than T
R
, the time which would have been
sent through e.
In that case, try to reuse the surplus T
R
− T
′
R
seconds on the source of e and its ancestors,
and send T
′
R
seconds through e. Go back in
the graph from the source of e, collecting nodes
with non-zero weights into C until a node with
more than one incoming or outgoing edge is
found. Increase the time limit of each collected
node by (T
R
− T
′
R
)w(n)/w(C), where w(C) =
∑
n∈C
R(n)w(n).
(b) If the target of e has not been visited before,
invoke this algorithm recursively, setting n to
the target of e and r(n) = T
R
.
7. Set the context parameter related to n to 0 if
w(n) = 0, and to (t(n) − m(n))/w(n) otherwise.
This is the effective slack per unit of weight dis-
tributed to n, considering reused surplus times.
3.2.3 Key Optimisations
The algorithm above uses several optimisations to im-
prove its performance. First of all, each path p is not
represented by its sequence of nodes, but by its con-
straint c(p) = (m(p),w(p)), saving much memory.
To select p
Mm
(n) at each node we need to know
the maximum m(p) for each path p ∈ P
S
(n), which
we will note as m(p
Mm
(n)). We can compute it in ad-
vance using (1). As it is recursive, we can evaluate (1)
incrementally, starting from the final nodes (for which
m(p
Mm
(n)) = 0) and going back up to the initial node
in reverse topological order:
m(p
Mm
(n)) = R(n)m(n)
+ max{m(p
Mm
(g(e)))|e ∈ o(n)}
(1)
To select p
ms
(n) at each node we need to know
the strictest path starting from it. We cannot compute
it in advance, as it depends on the time received by
the node, r(n), which is not known a priori. Instead,
we remove redundant paths from P
S
(n). We will call
this reduced set P
′
S
(n). A path p
a
∈ P
S
(n) is removed
when it is said to be always less or just as strict than
some other path p
b
∈ P
S
(n), independently of the time
received by n or the common ancestors of p
a
and p
b
.
We denote this by c(p
a
)
s(L)
c(p
b
), and define it for-
mally as follows:
(a,b)
s(L)
(c,d) ≡
∀t ∈ [0,L] ∀x ∈ [0,L] ∀y ≥ 0
a+ x ≤ t ∧ c + x ≤ t ∧
b+ y > 0∧d + y > 0 ⇒
t − (a+ x)
b+ y
≥
t − (c+ x)
d + y
(2)
We can simplify (2) into:
a ≤ c∧ (b ≤ d ∨ a < L∧ b > d ∧ (b− d)L ≤ bc− ad)
(3)
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
58

It can be proved that this defines a partial order (a re-
flexive, antisymmetric, and transitive binary relation)
on C(L). The proof is omitted for the sake of brevity.
Like m(p
Mm
(n)), P
′
S
(n) can also be computed in-
crementally by traversing the graph in reverse topo-
logical order. Let n
i
be a child of n and p
a
and p
b
be
two paths in P
S
(n
i
), so c(p
a
)
s(L)
c(p
b
). By defini-
tion, p
a
is less or just as strict as p
b
regardless of their
common ancestors, so hni+ p
a
will also be discarded
from P
′
S
(n) over hni + p
b
. This means that instead of
comparing every path in P
S
(n) for every node n, we
can build P
′
S
(n) by adding n at the beginning of the
paths in P
′
S
(n
i
), for every child n
i
of n, and then filter-
ing the redundant paths using
s(L)
.
Let max
s(L)
S select the paths in S which are not
always less or just as strict than any other (maximal
elements according to
s(L)
). We define P
′
S
(n) as:
P
′
S
(n) = max
s(L)
{(R(n)m(n) + M,R(n)w(n) + W)
|e ∈ o(n),(M,W) ∈ P
′
S
(g(e))}
(4)
Note that P
S
( f) = (0,0), where f is a final node.
3.2.4 Example
Previously, we defined the algorithm and described
the key optimisations performed. We will now apply
the algorithm to the example in Figure 2, producing
the diagram shown in Figure 3 . To save space, we
will shorten action names to their initials: “Evaluate
Order” will be simply “EO”.
First, m(p
Mm
(n)) and P
′
S
(n)) are precomputed:
• m(p
Mm
(CO)) = 0, P
′
S
(CO) = {(0,1)}.
• m(p
Mm
(PP)) = 0, P
′
S
(PP) = {(0,2)}.
• m(p
Mm
(CI)) = 0, P
′
S
(CI) = {(0,3)}.
• m(p
Mm
(SO)) = 0, P
′
S
(SO) = {(0, 2)}.
• m(p
Mm
(EO)) = 0.4, P
′
S
(EO) = {(0.4, 3)}.
After that, the algorithm sends the available sec-
ond (L = 1s) into the initial node and then into EO.
EO takes 0.4 seconds and sends the remaining 0.6 sec-
onds through the decision node. The next action in the
strictest path is CI, which takes 0.2 seconds and sends
0.4 seconds into PP. PP takes another 0.2 seconds and
sends the remaining 0.2 seconds to CO.
Once the strictest path is done, we back up and
proceed with the next strictest path, sending 0.4 sec-
onds into SO. At first, SO takes only 0.3 seconds, but
since CO received only 0.2 seconds before, we reuse
the extra 0.1 seconds into SO. The final time limit of
SO is 0.4 seconds. We back up and continue with the
empty branch for rejected orders, finding nothing to
annotate: we are done.
As for the context parameters:
swEO
is set to 0,
as w(EO) = 0.
swCI
,
swPP
and
swCO
are set to 0.2.
swSO
is set to 0.4: note that the initial slack per unit
of weight for SO was 0.3, but after reusing the extra
0.1 seconds, it changed to 0.4.
4 EVALUATION
The algorithms have been implemented using the Ep-
silon Object Language (EOL) (Kolovos et al., 2010)
and integrated into the Papyrus graphical UML ed-
itors (Eclipse Foundation, 2011). Code is available
at (García-Domínguez, 2011). In this section we will
analyse their restrictions and performance.
4.1 Restrictions
The inference algorithms are limited in several ways.
The most important restriction is that the graph
formed by the nodes of the activity must be acyclic,
which hinders the modelling of repetitive structures.
We have partially addressed this issue by using the at-
tribute rep of «GaStep» to indicate the expected num-
ber of repetitions of an action.
At first glance, the algorithm still requires to anno-
tate each action with some knowledge from the mod-
eller, so it would appear not to save much effort. How-
ever, the information annotated by the user on each
activity only depends on the action (minimum time
and weight) or control flow (probability) themselves,
instead of all the paths they are part of. In addition,
any sufficiently advanced tool can add the missing an-
notations with the default values set by the user. The
time limit inference algorithm also ensures that the
annotations are consistent with each other.
The algorithms do not take into account the fact
that the same behaviour might be reused in several
places: each action is assumed to be different from
the rest. A simple and conservative solution would be
simply taking the strictest constraint over all the oc-
currences of that behaviour. Integrating the “same be-
haviour” constraint would be interesting, but it might
considerably increase the cost of the algorithm.
4.2 Theoretical Performance
Having discussed the limitations of the algorithms,
we will now examine their theoretical performance.
Let us consider an activity with n nodes and e ∈
O(n
2
) edges, with O(n) incoming edges in each node.
The throughput inference algorithm is easy to anal-
yse: by going back from the final nodes to the initial
nodes, each node and edge in the activity needs to
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE
59

!
"#$%%&'
()(
*'(
%+,-./)
/)(
*'(
%,-.$0
$0
*'(
%,-.&&
&1'&#'
*'(
%,-.)
)(
*'(
%,-.$)
$)(
234(5
26
47(5
Figure 3: Running example after inferring time limits.
be visited exactly once. The throughput for the O(n)
join and merge nodes requires evaluating an expres-
sion in constant time over their O(n) incoming edges.
However, throughputs for the rest of the O(n + e)
nodes and edges can be computed in constant time.
Therefore, a conservative upper bound for the run-
ning time of the throughput inference algorithm is
O(n)O(n)+O(n+e)O(1) = O(n
2
). The running time
does not depend on the values of the annotations.
The time limit inference algorithm is harder to
analyse. Its performance depends both on the struc-
ture of the graph and the values of the annotations.
For this reason, we will use a specific kind of activity
to frame the analysis, which we call a fork-join ac-
tivity. As shown in Figure 4, it has an initial node,
I, followed by a sequence of f “levels”. Each level
has a fork node with two branches with a single ac-
tion, joined before the next level. The activity has
n = 2+4 f ∈ Θ( f) nodes and e = 1+5 f ∈ Θ( f) edges
in total, and there are 2
f
paths from the initial node
to the final node. These activities are inexpensive to
generate, as the number of nodes and edges grows lin-
early. At the same time, they can represent the worst
case of the algorithm, since the number of paths from
the initial node to the final node grows exponentially.
Having defined the structure of the activities, let
us analyse the algorithm by parts in the worst case:
• Computing m(p
Mm
(n)) in advance for each node
always takes O(1)O(n) = O(n) operations, as it
requires evaluating an arithmetic expression over
Figure 4: Example fork-join activity with f levels.
the O(1) incoming edges of each of the n nodes.
• Computing P
′
S
(n) in advance for each node is ac-
tually the most expensive part of the algorithm: in
the worst case, O(2
f
) paths need to be considered
at every node and selecting the strictest ones takes
O(4
f
) operations per node and O(n4
f
) in total.
• The last step depends on the number of elements
of P
′
S
(g(e)) for each edge e in the graph: in the
worst case, |P
′
S
(g(e))| = |P
S
(g(e))| for every node
and O(n2
f
) operations are required.
Joining the three parts of the algorithm yields a
time of O(n4
f
) operations in the worst case for a fork-
join activity. The absolute worst case is very expen-
sive but also very rare, as shown in the next section.
4.3 Empirical Performance
Previously, we concluded that the throughput algo-
rithm had polynomial cost regardless of the anno-
tations, and that the time limit inference algorithm
could reach exponential cost, depending on the an-
notations. In this section we will study how close are
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
60

Figure 5: Average running times in milliseconds over 10
runs of the throughput inference algorithm, using fixed and
random annotations, by number of levels.
Figure 6: Average running times in milliseconds over sev-
eral runs of the time limit inference algorithm (10 for fixed
annotations, 100 for random annotations), by number of
levels.
the average times to this absolute worst case.
Our first step was to measure the performance of
the algorithms using fork-join activities with 1 to 25
levels. We ran the algorithms on these activities re-
quiring 1s response time when 1 request was received
per second. The actions were annotated in two ways:
either using a fixed minimum time limit and weight
(0 and 1, respectively) or using uniformly distributed
random values, so the minimum time limits were con-
sistent and weights were between 0 and 1. To simplify
the analysis, each action had rep set to 1.
The results are shown in Figures 5 and 6. Fig-
ure 5 confirms that the time required for the through-
put inference algorithm grows linearly, regardless of
the annotations. Figure 6 suggests that the average
times for fixed and random annotations are quite far
Figure 7: Percentage of sampled 3-level fork-join activities
with a certain number of incomparable top-level paths, by
global time limit.
from the O(n4
f
) absolute worst case.
It is interesting to note that when the minimum
time limit is equal to 0 in all actions, the partial order
in (3) can be simplified to a ≤ c, which is a total or-
der. Therefore, these fixed annotations are instances
of the best case of the time limit inference algorithm,
in which all paths are comparable. As shown in Fig-
ure 6, the time limit inference algorithm required 400
milliseconds on average to annotate a fork-join activ-
ity with fixed annotations and 25 levels.
On the other hand, using uniformly distributed
random annotations resulted in much larger running
times, with 10 seconds required on average to anno-
tate a fork-join activity with 25 levels. Nevertheless,
Figure 6 does not grow as quickly as would be ex-
pected from the O(n4
f
) absolute worst case.
This suggests that removing redundant paths re-
duces the impact of the absolute worst case. How-
ever, its effectiveness depends on the relative magni-
tude of the minimum time limits and weights with re-
gards to the global time limit L. The left operand of
(b− d)L < bc− ad, part of (3), grows as L increases
and reduces the number of comparable pairs of paths.
We performed an additional study to clarify how
common the absolute worst case was and study its
relationship with L. We sampled with L = 0.5s and
L = 1.5s the space of all fork-join activities with 3 lev-
els which contained a 2-level fork-join with 4 incom-
parable paths. Minimum time limits for the actions
ranged from 0 to min{L, 1} , in steps of 0.1s. Weights
ranged from 0 to 10, in steps of 1 unit. Inconsistent
graphs were discarded. For each activity, we mea-
sured the number of incomparable paths at the initial
node (“top-level paths”): in a 3-level fork-join activ-
ity, there can be between 1 and 2
3
= 8 such paths.
Evaluating 1.99× 10
6
fork-join activities for L =
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE
61

0.5s and 7.16× 10
9
for L = 1.5s produced the results
in Figure 7. It is interesting to note that for L = 1.5s,
while 31.842% of all 1-level fork-join activities were
in the worst case, only 2.492% 2-level fork-join ac-
tivities were in the worst case. With 3 levels, no fork-
join activities were in the worst case with L = 0.5s,
and only 0.047% were in the worst case with L = 1.5s.
This suggests that the absolute worst case becomes
harder to find as graphs become more complex, ex-
plaining why average times did not grow exponen-
tially in Figure 6. Additionally, it indicates that the
worst case becomes more common as L grows in re-
lation to the values used in the annotations.
5 RELATED WORK
Obtaining the desired level of performance has been
a regular concern since the development of the first
computer systems, as shown by the early survey
in (Lucas, 1971). There are basically two approaches:
evaluating a model of a prospective system, or mea-
suring the performance of an implemented system.
These approaches are complementary: using analytic
models reduces the risk of implementing an ineffi-
cient software architecture, which is expensive to re-
work (Smith and Williams, 2003). When the system
is implemented, measuring its performance is more
accurate, and can detect not only design issues, but
also bad coding practices and unexpected workloads
or platform issues. Our work adapts the MARTE
profile, a standard notation used for modeling non-
functional requirements and creating analytic models
from them, to generate the performance requirements
for testing each part of the system.
Using analytic models requires highly specialised
knowledge and notations. Widespread adoption of
UML as a de facto standard notation has prompted
researchers to derive their analytic models from UML
models, first with ad hoc annotations and later con-
solidating on the standard extensions to UML, such
as QoS/FT (OMG, 2008) or SPT (OMG, 2005). The
survey in (Woodside, 2007) reviews many of the
approaches before MARTE replaced SPT in 2009.
Since then, MARTE has been used for many pur-
poses, such as deriving process algebra specifica-
tions (Tribastone and Gilmore, 2008) and extended
Petri networks (Yang et al., 2010) or detecting data
races (Shousha et al., 2009), among others. We se-
lected MARTE as it is based on UML, it is being ac-
tively used and offers both pre-made annotations (like
SPT) and a generic framework (like QoS/FT).
Bernardi et al. have defined the Dependability and
Analysis Modeling sub-profile for MARTE (Bernardi
et al., 2009). It has been combined with the standard
GQAM and PAM sub-profiles of MARTE to evaluate
the risk that a soft real-time system does not meet its
time limits (Bernardi et al., 2010). Our work also han-
dles time limits, but our focus is different: we help the
tester “fill in the blanks” using the available partial in-
formation. We use a model of the system to generate
some of the parameters of the performance test cases.
Alhaj and Petriu generated intermediate perfor-
mance models from a set of UML diagrams anno-
tated with the MARTE profile, describing a service-
oriented architecture (Alhaj and Petriu, 2010): UML
activity diagrams model the workflows, UML com-
ponent diagrams represent the architecture and UML
sequence diagrams detail the behaviour of each action
in the workflows. In our previous work, we similarly
modeled workflows in a service-oriented architecture
using an ad hoc notation based on UML activity di-
agrams (García-Domínguez et al., 2010). However,
our approach does not model the resources used by
the system: we assume tests are performed in an en-
vironment which mimics the production environment.
6 CONCLUSIONS AND FUTURE
WORK
Software needs to meet its performance requirements
in addition to its functional requirements. To achieve
this goal, several approaches can be combined: the
expected performance can be estimated using an early
model, or the actual performance of the system can be
measured. Currently, the research community is con-
verging on the UML MARTE profile (OMG, 2009)
as a standard notation to drive early performance and
scheduling analysis. On the other hand, performance
testing requires expectations to be defined for each
part of the system. However, these are usually only
available for high-level components: developers need
to manually translate these to lower-level require-
ments for the smaller subcomponents.
In this work, we have adapted and improved the
algorithms in (García-Domínguez et al., 2010) to op-
erate on MARTE-annotated UML activity diagrams,
inferring performance requirements from a global an-
notation and some local ones. One algorithm infers
throughputs and has polynomial cost in relation to the
number of nodes of the activity. The other infers time
limits and its worst case has exponential cost, as it
may need to enumerate all paths from the initial node
to the final nodes. However, further analysis of the
average case suggests that this worst case is very rare,
and becomes even harder to find as graphs become
more complex. This is because the time limit infer-
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
62

ence algorithm discards redundant subpaths using a
partial order relation.
For the next versions of the algorithms, we intend
to handle nested activities, so the user can describe
the system as a hierarchy of components and infer
time limits and throughputs in a top-down approach.
Handling actions which are repeated in several places
would be interesting, but the cost of the algorithms
might increase. After improving the algorithms, our
main priority is to assist in the generation of test
cases for an existing tool, transforming the MARTE-
annotated UML model into text. One approach is to
generate performance tests which wrap existing func-
tional tests. Another approach is to partially generate
test plans for existing performance testing tools.
ACKNOWLEDGEMENTS
This work was partly funded by the research schol-
arship PU-EPIF-FPI-C 2010-065 of the University of
Cádiz.
REFERENCES
Alhaj, M. and Petriu, D. C. (2010). Approach for generat-
ing performance models from UML models of SOA
systems. In Proc. of the 2010 Conference of the Cen-
ter for Advanced Studies on Collaborative Research,
CASCON ’10, pages 268–282, New York, NY, USA.
ACM.
Bernardi, S., Campos, J., and Merseguer, J. (2010). Timing-
Failure risk assessment of UML design using time
petri net bound techniques. Industrial Informatics,
IEEE Transactions on, PP(99):1.
Bernardi, S., Merseguer, J., and Petriu, D. C. (2009). A de-
pendability profile within MARTE. Software & Sys-
tems Modeling.
Eclipse Foundation (2011). Homepage
of the Eclipse MDT Papyrus project.
http://www.eclipse.org/modeling/mdt/papyrus/.
Erl, T. (2008). SOA: Principles of Service Design. Prentice
Hall, Indiana, EEUU.
García-Domínguez, A. (2011). Home-
page of the SODM+T project.
https://neptuno.uca.es/redmine/projects/sodmt.
García-Domínguez, A., Medina-Bulo, I., and Marcos-
Bárcena, M. (2010). Inference of performance con-
straints in Web Service composition models. CEUR
Workshop Proc. of the 2nd Int. Workshop on Model-
Driven Service Engineering, 608:55–66.
Kolovos, D., Paige, R., Rose, L., and Polack, F. (2010). The
Epsilon Book. http://www.eclipse.org/gmt/epsilon.
Lucas, H. (1971). Performance evaluation and monitoring.
ACM Computing Surveys, 3(3):79–91.
OMG (2005). UML Profile for Schedulabil-
ity, Performance, and Time (SPTP) 1.1.
http://www.omg.org/spec/SPTP/1.1/.
OMG (2008). UML Profile for Modeling Quality of Service
and Fault Tolerance Characteristics and Mechanisms
(QFTP) 1.1. http://www.omg.org/spec/QFTP/1.1/.
OMG (2009). UML Profile for Modeling and Analysis
of Real-Time and Embedded systems (MARTE) 1.0.
http://www.omg.org/spec/MARTE/1.0/.
Shousha, M., Briand, L., and Labiche, Y. (2009). A
UML/MARTE model analysis method for detection
of data races in concurrent systems. In Model Driven
Engineering Languages and Systems, volume 5795
of Lecture Notes in Computer Science, pages 47–61.
Springer Berlin / Heidelberg.
Smith, C. U. and Williams, L. G. (2003). Software perfor-
mance engineering. In Lavagno, L., Martin, G., and
Selic, B., editors, UML for Real: Design of Embed-
ded Real-Time Systems, pages 343–366. Kluwer, The
Netherlands.
Tribastone, M. and Gilmore, S. (2008). Automatic extrac-
tion of PEPA performance models from UML activ-
ity diagrams annotated with the MARTE profile. In
Proc. of the 7th Int. Workshop on Software and Per-
formance, pages 67–78, Princeton, NJ, USA. ACM.
Weyuker, E. J. and Vokolos, F. I. (2000). Experience with
performance testing of software systems: Issues, an
approach, and case study. IEEE Transactions on Soft-
ware Engineering, 26:1147–1156.
Woodside, M. (2007). From annotated software designs
(UML SPT/MARTE) to model formalisms. In Proc. of
the 7th Int. Conference on Formal Methods for Perfor-
mance Evaluation, pages 429–467, Bertinoro, Italy.
Springer-Verlag.
Woodside, M., Franks, G., and Petriu, D. (2007). The fu-
ture of software performance engineering. In Proc. of
Future of Software Engineering 2007, pages 171–187.
Woodside, M., Petriu, D. C., Petriu, D. B., Shen, H., Israr,
T., and Merseguer, J. (2005). Performance by uni-
fied model analysis (PUMA). In Proc. of the 5th Int.
Workshop on Software and Performance, pages 1–12,
Palma, Illes Balears, Spain. ACM.
Yang, N., Yu, H., Sun, H., and Qian, Z. (2010). Modeling
UML sequence diagrams using extended Petri nets. In
Proc. of the 2010 Int. Conference on Information Sci-
ence and Applications, pages 1–8.
MODEL-DRIVEN DESIGN OF PERFORMANCE REQUIREMENTS WITH UML AND MARTE
63
