TRANSFORMING ATTRIBUTE AND CLONE-ENABLED

FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

Raúl Mazo

CRI, Panthéon Sorbonne University, 90, rue de Tolbiac, 75013 Paris, France

Departamento de Ingeniería de Sistemas, Universidad de Antioquia, Medellín, Colombia

Camille Salinesi, Daniel Diaz

CRI, Panthéon Sorbonne University, 90, rue de Tolbiac, 75013 Paris, France

Alberto Lora-Michiels

Baxter International Inc., Lessines, Belgium

Keywords: Requirement engineering, Product line models, Feature models, Transformation, Constraint programming.

Abstract: Product line models are important artefacts in product line engineering. One of the most popular languages to

model the variability of a product line is the feature notation. Since the initial proposal of feature models in

1990, the notation has evolved in different aspects. One of the most important improvements allows specify

the number of instances that a feature can have in a particular product. This improvement implies an

important increase on the number of variables needed to represent a feature model. Another improvement

consists in allowing features to have attributes, which can take values on a different domain than the

boolean one. These two extensions have increased the complexity of feature models and therefore have

made more difficult the manually or even automated reasoning on feature models. To the best of our

knowledge, very few works exist in literature to address this problem. In this paper we show that reasoning on

extended feature models is easy and scalable by using constraint programming over integer domains. The aim

of the paper is double (a) to show the rules for transforming extended feature models into constraint programs,

and (b) to demonstrate, by means of 11 reasoning operations over feature models, the usefulness and benefits

of our approach. We evaluated our approach by transforming 60 feature models of sizes up to 2000 features

and by comparing it with 2 other approaches available in the literature. The evaluation showed that our

approach is correct, useful and scalable to industry size models.

1 INTRODUCTION

Requirements Engineering is the process of

discovering system purpose by identifying

stakeholders and their needs, and documenting these

in a way that is amenable to reasoning,

communication, and subsequent implementation

(Nuseibeh and Easterbrook, 2000). When this

process is achieved in the context of Product Lines

(PL), its complexity and difficulty is much higher

since there are several products to consider, which

imply to manage the relationships of communality

and variability between them. One of the most

popular notations to specify the common and

variable requirements of a software product line is

the Feature Models (FMs). In the context of PLs,

FMs are used for product derivation, variability

reasoning and code generation (Kang et al., 1990),

(Van Deursen and Klint, 2002). In these contexts,

FMs are usually transformed to executable code in

order to reason on them (Batory, 2005), (Benavides

et al., 2005), (Benavides et al., 2007), (Benavides et

al., 2010), (Van Deursen and Klint, 2002), (Karataş et

al. 2010), (Salinesi et al., 2010). Since their first

introduction in 1990 as a part of the Feature-

Oriented Domain Analysis (FODA) method (Kang et

188

Mazo R., Salinesi C., Diaz D. and Lora-Michiels A..

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS OVER FINITE DOMAINS.

DOI: 10.5220/0003509301880199

In Proceedings of the 6th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2011), pages 188-199

ISBN: 978-989-8425-57-7

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

al., 1990), several extensions have been proposed to

improve and enrich the expressiveness of FMs. The

first one was the introduction in the basic FODA

notation of cross-tree dependencies (requires and

excludes), to put constraints on features. The second

and the third extensions consisted in the introduction

of attributes (Diaz and Codognet, 2001), (Benavides

et al. 2005b) and cardinalities (feature and group

cardinalities) (Czarnecki et al. 2005), (Djebbi and

Salinesi, 2007), (Van Hentenryck, 1989). FMs with

these three extensions are called extended feature

models. Despite their pertinence for the industry,

most of the reasoning approaches on FMs do not

consider the last two extensions, or at best partially

(Benavides et al., 2010). In this paper we propose an

approach based on constraint programming that fills

this gap by handling reasoning on extended FMs.

In the last few years, Constraint Programming

(CP) has attracted attention among experts from

many areas because of its potential for solving hard

real life problems. Not only it is based on a strong

theoretical foundation but it is also attracting a

widespread commercial interest as well, in

particular, in areas of modelling heterogeneous

optimisation and satisfaction problems. In the PL

domain, several authors have proposed to use CP to

represent FMs but without attributes and

cardinalities (Batory, 2005), (Benavides et al., 2005)

or with lacks on quality representation and

implementation (Karataş et al., 2010).

The approach presented in this paper uses

constraint programming to represent extended

feature models with the purpose of reasoning on

them by using an existing constraint solver. Details

about reasoning operations on FMs are out of scope

of this paper. We begin describing extended feature

models and developing a relevant example to

illustrate the transformation process of extended

FMs into constraint programs and the subsequent

reasoning operations that can be executed on them.

We finally present an initial evaluation of our

approach. In our evaluation we transform to CP 60

feature models of sizes up to 2000 features. This

transformation has been compared with two other

approaches from the literature. The results obtained

by this experiment show that our approach is

pertinent because it fixes errors of one of the

existing approaches. The results also show that our

approach is (i) scalable to important size models,

which can be transformed into CPs in only few

seconds; and (ii) correct, compared with the already

state of the art approaches (Benavides 2007),

(Mendoça et al., 2009). We conclude the paper with

a discussion of related works, then of open issues

and we conclude with an outlook on future works.

2 BACKGROUND AND

MOTIVATION

2.1 Extended Feature Models

A FM defines the valid combinations of features in a

SPL, and is depicted as a graph-like structure in

which nodes represent features, and edges the

relationships between them (Kang et al., 2002). A

feature is a prominent or distinctive user-visible

aspect, quality, or characteristic of a software system

(Kang et al., 1990). A feature can have zero or more

attributes (Van Deursen and Klint, 2002), (Ziadi et

al., 2003). Cardinality-based feature models

(Czarnecki et al., 2005) allow specifying individual

cardinalities for each feature and group cardinalities

grouping bundles of features. In this paper, we use

the semantic of feature models proposed by

(Schobbens et al., 2007) and cardinality-based

feature models proposed by (Michel et al., 2011).

Components of a FM can be related among them by

means of the following relationships:

• Feature cardinality: Is represented as a sequence

of intervals [min..max] determining the

number of instances of a particular feature that

can be part of a product. Each instance is called a

clone.

• Attribute: Although there is no consensus on a

notation to define attributes, most proposals agree

that an attribute is a variable with a name, a

domain, and a value (consistent with the domain)

at a given configuration time.

• Father-child relationship, there are two kinds:

o Mandatory: Given two features F1 and F2,

F1 father of F2, a mandatory relationship

between F1 and F2 means that if the F1 is

selected, then F2 must be selected too and

vice versa.

o Optional: Given two features F1 and F2, F1

father of F2, an optional relationship between

F1 and F2 means that if F1 is selected then

F2 can be selected or not. However, if F2 is

selected, then F1 must also be selected.

o Requires: Given two features F1 and F2, F1

requires

F2 means that if F1 is selected in

product, then F2 has to be selected too.

Additionally, it means that F2 can be selected

even when F1 is not.

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

189

o Exclusion: Given two features F1 and F2,

F1 excludes F2 means that if F1 is selected

then F2 cannot to be selected in the same

product. This relationship is bi-directional: if

F2 is selected, then F1 cannot to be selected

in the same product.

• Group cardinality: A group cardinality is an

interval denoted <n..m>, with n as lower bound

and m as upper bound limiting the number of

child features that can be part of a product when

its parent feature is selected. If one of the child

features is selected, then the father feature must

be selected too.

As a running example, we illustrate cardinality

and non-cardinality based feature models with a

hypothetical case of a Movement Control System

(MCS) of a car. This example is a simplified extract

of a real FM developed with one of our industrial

partners. A more complete extract of the model is

explained in (Salinesi et al., 2010b) and (Salinesi et

al., 2011). In Figure 1, we present the cardinality-

based FM of the allocation of hardware resources for

a car MCS. A MCS is composed of one or several

sensors, one or two processors and one or two slots

of internal memory. Sensors are used to measure the

speed and position of a car by means of two features

called Speed Sensor

and Position Sensor,

respectively. Speed Sensor is represented as a

mandatory feature (with a feature cardinality

[1..1]). And Position Sensor is represented

as an optional feature (with a feature cardinality

[0..4]). These two features are related by means

of a requires relationship. To compute the location

of a car, the MCS uses one or two processors, each

one associated by means of a mandatory relationship

with one or two slots of

Internal Memory.

Internal memory can take the values of 128, 512 or

1024 as specified in its attribute Size

eedSensor

Movement Control System

PositionSensor

Processor

[0..4]

[1..1]

[1..2]

Internal Memor

[1..2]

Size:{128,512,1024}

Figure 1: Example of feature model. Extract of an

allocation of resources for a movement control system of a

car.

2.2 Constraint Programming

in a Nutshell

Constraint Programming (CP) emerged in the 1990’s

as a successful paradigm to tackle complex

combinatorial problems in a declarative manner

(Van Hentenryck, 1989). CP extends programming

languages with the ability to deal with logical

variables of different domains (e.g. integer, real or

boolean) and specific declarative relations between

these variables called constraints. These constraints

are solved by specialized algorithms, adapted to

their specific domains and therefore much more

efficient than generic logic-based engines. A

constraint is a logical relationship among several

variables, each one taking a value in a given domain

of possible values. A constraint thus restricts the

possible values that variables can take.

A Constraint Satisfaction Problem (CSP) is

defined as a triple (X, D, C), where X is a set of

variables, D is a set of domains, i.e. finite sets of

possible values (one domain for each variable), and

C a set of constraints restricting the values that the

variables can simultaneously take. Classical CSPs

usually consider finite domains for the variables

(integers) and solvers propagation-based methods

(Bessiere, 2006), (Van Hentenryck, 1989). Such

solvers keep an internal representation of variable

domains and reduce them monotonically to maintain

a certain degree of consistency with reference to the

constraints.

In modern Constraint Programming languages

(Diaz and Codognet, 2001), (Van Hentenryck,

1989), many different types of constraints exist and

are used to represent real-life problems: arithmetic

constraints such as X + Y < Z, symbolic

constraints like atmost(N,[X1,X2,X3],V)

which means that at most N variables among

[X1,X2,X3] can take the value V, global

constraints like alldifferent(X1,X2,…,

Xn)meaning that all variables should have different

values, and reified constraints that allow to reason

about the truth-value of a constraint. Solving

constraints consists in (a) reducing the variable

domains by propagation techniques that will

eliminate inconsistent value within domains, then

(b) finding values for each constrained variable in a

labeling phase, that is, iteratively grounding

variables (fixing a value for a variable) and

propagating its effect onto other variable domains

(by applying again the same propagation-based

techniques). The labeling phase can be improved by

using heuristics concerning the order in which

ENASE 2011 - 6th International Conference on Evaluation of Novel Software Approaches to Software Engineering

190

variables are considered as well as the order in

which values are tried in the variable domains. See

(Diaz and Codognet, 2001) and (Schulte and

Stuckey, 2008) for more details.

2.3 Motivating Scenario

The graphical representation of FMs makes

reasoning difficult. Proposals have thus been made

to represent FMs in languages that allow automatic

reasoning (Batory, 2005), (Benavides et al., 2005),

(Czarnecki et al., 2005), (Van Deursen and Klint,

2002), (Salinesi et al., 2010). Our approach uses thi

strategy and uses constraint programming as the

language to represent models and configure, analyse

and verify them. Based on a recent literature review

of analysis operations (Benavides et al., 2010) and

on our previous works (Mazo et al., 2011), (Salinesi

et al., 2010) on product line models verification, we

implemented a collection of reasoning operations.

These reasoning operations are completely

automated in our tool VariaMos. VariaMos is an

Eclipse plug-in that implements the following

operations (see (Benavides et al., 2010) for detailed

definitions of these operations):

• Analysis of FMs satisfiability. A FM is

satisfiable if at least one product is represented

by the FM. This operation may be helpful for

managers and engineers because a PLM not

allowing configure product is a useless model.

• Calculating the number of valid products

represented by the FM. This operation may be

useful for determining the richness of a FM. For

instance, in our running example, 433 products

can be configured.

• Calculating product line commonality. This is

the ratio between the number of products in

which the set of variables is present and the

number of products represented in the FM. In

our running example Commonality is equal to 1.

• Calculating Homogeneity. By definition

Homogeneity = 1 - (#unicFeas /

#products).

where #unicFeas is the number of unique

features in one product and #products

denotes the total number of products

represented by the FM. In our running example

Homogeneity is equal to 1.

• Detection of errors in a FM. Errors are

undesirable situations in a FM, as for instance

features that can never be used in a

configuration (dead features), redundant

features and constraints and false optional

features as in Position Sensor in our

running example. False optional features are

represented as optional (feature cardinality

[0..4] for Position Sensor) but are

present in all products of the FM (because is

required by a feature like Speed Sensor

which appears in all configurations).

The following operations with respect to

configuration of PLMs:

• Finding a valid product if any. A valid product

is a product, derived from the FM, that respects

all the FM’s constraints. For instance, finding a

product of the MCS example depicted

previously in the FM of Figure 1 could retrieve

the product P1 = {one Speed Sensor,

two Position Sensors; one

Processor; one Internal Memory

of 128; one Internal Memory of

1024}

• Obtaining the list of all valid products

represented by the FM, if any exist. This

operation may be useful to compare two product

line models. For the sake of space, the

comprehensive list cannot be presented in this

paper.

• Checking validity of a configuration. A

configuration is a collection of features and may

be partial or total. A valid partial configuration

is a collection of features respecting the

constraints of the FM but not necessary

representing a valid product. A total

configuration is a collection of features

respecting the constraints of a FM and where no

more features need to be added to conform a

valid product. This operation may be useful to

determine if there are not contradictions in a

collection of features. In our running example,

the product P = {one Position

Sensor; two Processor; one

Internal Memory of 512} is not valid

because the feature Speed Sensor is mandatory

(feature cardinality [1..1]).

• Executing a dependency analysis. It looks for all

the possible solutions after assigning some fix

value to a collection of features. In our running

example, if we select two clones of Position

Sensor, the number of products with this

requirement is 108.

• Specifying external requirements specifications

for configurations using constraints (for

instance, definition of a maximal or minimal

value, definition of one dependent value among

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

191

to variables such as Size > 512 ⇒

2*Position Sensor)

The following application level analysis operations

was implemented too:

• Checking if a product belongs to the set of

products represented by the FM. This operation

may be useful to determine whether a given

product is available in a software product line.

For instance, P1 = {one Speed Sensor,

two Position Sensors; one

Processor; one Internal Memory

of 128; one Internal Memory of

1024}, is a valid product of our FM used as

running example, but P2 = {three Speed

Sensor, two Position Sensors;

one Processor; one Internal

Memory of 128; one Internal

Memory of 1024} is not.

Constraint programming is efficient in solving

optimization problems. Our approach supports the

specification and analysis of goals such as “identify

the optimal configuration with respect to cost (min

goal) and benefit (max goal) feature attributes” to

detect “optimal” products and support decision

making during the configuration activity as we

presented in previous works such as (Djebbi and

Salinesi, 2007), (Salinesi et al., 2010b).

3 CONVERTING FEATURE

MODELS TO CONSTRAINT

PROGRAMS

Both, semantic and structure of product line models

can be specified as constraint logic programs. In this

paper, we are interested in represent the semantic of

FMs by means of constraint programs and not the

structure as do Mazo et al. (2011b). Thus, the

semantic of a product line model can be specified as

a constraint program (Salinesi et al., 2010b) by

means of: (i) a set of variables X={x

,...,x

};

(ii) for each variable x

, a finite set D

of possible

values (its domain); and (iii) a set of constraints

restricting the values that they can simultaneously

assume. A variable in a PLM has a domain of

values, and the result of the configuration process is

to provide it a value. In particular, feature models

are represented in CP with (i) variables, that

correspond to features, attributes, and instances of

features defined by a feature cardinality; (ii)

domains of variables; and (iii) with constraints for

the relationships among the variables. These

constraints can be boolean, arithmetic, symbolic and

reified. The representation of feature models as

constraint programs applies the following principles:

• Each feature is represented as a boolean (0,1)

CP variable.

• Each attribute is represented as a CP variable, the

domain of the attribute belongs the domain of the

CP variable.

• Each feature cardinality [m..n] determines (i) a

collection of n variables associated to the feature

of which this cardinality belongs; and (ii) a

constraint restricting the minimum (m) and the

maximum (n) number of variables that can

belong to a product in a certain moment.

• The domains of all variables are finite and can be

composed of integer values. When a variable

takes the value of zero, it means that the variable

is not selected, when a variable takes another

value of its domain (different to zero) the variable

is considered as selected.

• Every relationship is implemented as a constraint.

Our constraint program representation of feature

models follows the next mapping rules:

• Feature cardinality: Let P be a feature with a

feature cardinality [m, n], then we create a CP

variable P, a collection of n CP variables, one for

each possible clone of P and an association

between P and each of its clines. It is: {P, P

, ..., P

} ∈ {0,1} ˄ (P ⇒ P

≥

0) ˄ (P

⇒ P) for i=1,…,n

• Attribute: Let P be a feature and A

, A

, ...,

a collection of attributes of P, each one with a

particular domain D

, D

, ..., D

respectively. The constraints to represent this case

are: P ⇔ A

> 0, A

∈ D

for i=1…n.

• Requires: Let P and C be two features, where P

requires C. If P has a feature cardinality [m..n]

with {P

, P

, ..., P

} ∈ {0,1} clones

of P, the constraint is: P

⇒ C, P

⇒ C,

..., P

⇒ C. On the contrary, if P does not

have feature cardinality, the equivalent constraint

is: P

⇒ C, which means that if P is selected, C

has to be selected as well, but not vice versa.

• Exclusion: Let P and C be two features, where P

excludes C. If P has a feature cardinality [m..n]

with {P

, P

, ..., P

} ∈ {0,1} clones

of P, the constraint is: P

* C = 0, P

* C

= 0, ..., P

* C = 0. In the contrary, if

P does not have feature cardinality, the equivalent

constraint is: P * C = 0. Which means that if

ENASE 2011 - 6th International Conference on Evaluation of Novel Software Approaches to Software Engineering

192

P is selected (value > 0), then C must be equal to

zero, also both can be not selected (equal to zero).

• Group cardinality: Let C

, C

, …, and C

features with domain {0,1}, with the same

parent P, and <m, n> the group cardinality in a

decomposition with group cardinality. The

equivalent constraint is: P

⇒ (m ≤ C

+ C

… + C

≤ n), which means that at least m and

at most n children features must be selected. Note

that the dependencies of C

, C

, …, and C

with their parent (with feature cardinality or not)

are constrained by means of the following father-

child relationship.

• Father-child relationship: Let C be a feature with

a feature cardinality [cm, cn] and a parent P

with feature cardinality [pm, pn]. Then we

generate by each clone of P ({P

, P

, ...,

} ∈ {0,1}), cn boolean CP variables {C

, ..., C

} ∈ {0,1}, each one

corresponding to a clone of C.

The constrains for the clones of P are:

⇒ P for i=1,…,pn

And the constraints among each clone of P and

the clones of C are:

⇒ (C

⇒ C) for i=1,…,cn ˄

⇒ (C

⇒ C) for i=1,…,cn ˄ …

⇒ (C

⇒ C) for i=1,…,cn ˄

⇒ (cm ≤ C

+ C

+ … + C

≤ cn)

And to finish, we represent the relationship

between P and C according to its type. Mandatory

when cm > 0 :

P ⇔ C

and optional when cm = 0 :

C ⇒ P

This means that in a particular configuration,

when a clone of the feature P is chosen, at least

cm and at most cn clones of the child feature C

must be selected and if at least one clone of C is

selected, C must be selected as well. In this paper

we use the semantic of cardinality-based FMs

proposed by Michel et al., (2011).

Let us use the previous rules to represent our

running example in Figure 1. The first step is to

create a list with the CP variables of each feature

according to its feature cardinality and its attributes,

as follows:

[MovementControlSystem, SpeedSensor,

PositionSensor, PositionSensor1,

PositionSensor2, PositionSensor3,

PositionSensor4, Processor, Processor1,

Processor2, InternalMemory1,

InternalMemory2, Size]

The second step is to constrain the domains of each

CP variable created in step one, according to its

corresponding domain, and the value 0 to indicate

that the variable has the possibility to not be chosen

in a particular product:

[MovementControlSystem, SpeedSensor,

PositionSensor, PositionSensor1,

PositionSensor2, PositionSensor3,

PositionSensor4, Processor,

Processor1, Processor2,

InternalMemory1, InternalMemory2] ∈

{0,1} ˄

Size ∈ {0, 128,512,1024}

The next step is to constrain the relationship among

a feature and its clones as a constraint where each

clone has the possibility to be selected or not, but if

on clone is selected the cloned feature must be

selected as well:

PositionSensor1 ⇒ PositionSensor ˄

PositionSensor2 ⇒ PositionSensor ˄

PositionSensor3 ⇒ PositionSensor ˄

PositionSensor4 ⇒ PositionSensor ˄

Processor1 ⇒ Processor ˄

Processor2 ⇒ Processor ˄

InternalMemory1 ⇒ InternalMemory ˄

InternalMemory2 ⇒ InternalMemory

Next, we constrain the clones of each feature

according to the corresponding feature cardinality:

PositionSensor ⇒ (0 ≤

PositionSensor1 + PositionSensor2 +

PositionSensor3+PositionSensor4 ≤ 4)˄

Processor ⇒ ( 1 ≤ Processor1 +

Processor2 ≤ 2) ˄

InternalMemory ⇒ (1 ≤

InternalMemory1 + InternalMemory2 ≤2)

Next we map the father-child relationships among

features to the following constraints. Features where

their feature cardinality has the value 0 (e.g.,

Position Sensor with a feature cardinality

[0..4]), must be represented as optional features.

MovementControlSystem ⇔SpeedSensor ˄

MovementControlSystem ⇔ Processor ˄

Processor ⇔ InternalMemory ˄

(MovementControlSystem ⇒

PositionSensor ≥ 0) ˄ (PositionSensor

⇒ MovementControlSystem)

Note that we related the variable Processor, and

not its instances, with InternalMemory. It is

because Processor and its instances are related

with a double implication, then every affectation of

Processor will affect in the same way its

instances and vice versa. We continue with the

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

193

relations among features and their attributes:

InternalMemory ⇔ Size > 0

Indicating that if the InternalMemory is selected

in a product

(= 1, implicit), then the value of Size

must be also selected (

> 0) and vice versa.

Finally, we map the requires and excludes (there is

no excludes relations in the model of Figure 1)

relations to their constraints:

SpeedSensor ⇒ PositionSensor

4 IMPLEMENTATION AND

EVALUATION

4.1 Feasibility

With regards to the source of the FMs to transform

into constraint programs, one of two strategies can

be used to implement this transformation. The first

strategy consists on using an Application

Programming Interface (API) to navigate on the FM

tree structure and recuperate each feature and its

associated relationships. Each time we gather a

feature (with or without attributes) or a relationship

between two features, we transform them into

constraint programs by using the transformation

rules presented in this paper. The second approach

consists on using a transformation engine to

transform original FMs into CPs. This approach

must be used when no API to navigate in the FMs is

available and when we dispose of the well-defined

meta-models of the input and the target language.

Our transformation patterns were implemented as

Atlas Transformation Language (ATL) rules and the

output models were transformed from XML

Metadata Interchange (XMI) files to CPs. Both

strategies are automated in our tool VariaMos

(Mazo, 2010) and their use in our experiment are

explained below.

4.1.1 Fist Strategy; by using a Navigation

API

48 of our 60 FMs we used to test our approach come

from SPLOT (Mendça et al., 2009). So, to

implement the first transformation strategy, we used

the Mendonca’s parser for SPLOT’s XML-based

feature models into constraint programs.

4.1.2 Second Strategy; by using a

Transformation Engine

12 of our 60 FMs are real world examples from our

passed and on-going industrial collaboration. These

models, with sizes up to 180 features, do not provide

any particular API to navigate on them, so, the

second strategy must be used to convert them into

constraint programs.

This strategy implies the use of two meta-

models, the meta-model of the source language and

the meta-model of the target language. The meta-

model we used for the source language, it is, for the

FM language is presented in (Salinesi et al., 2010).

And the meta-model to represent the CP language is

depicted in Figure 2.

Figure 2: CP meta-model.

According to CP meta-model, a CP is a

composition of constraints and variables. Variables

are related among them in one or several constraints

in the context of a constraint program and can or not

have a domain, variables that does not have domain

are considered as Booleans.

Two examples of ATL rules allowing transform

features into CP variables and group cardinality

boundaries into CP constants are respectively

presented as follows. Not all rules are presented here

for the sake of place.

rule Feature2Variable {

from s : Features!Feature

to t1 : CPs!Variable (

name <- s.name,

haveDomain <-

s.haveCardinality-> collect(e |

thisModule.Cardinality2Domain(e)))

}

lazy rule Cardinality2Domain {

from s : Features!Cardinality

to cardi : CPs!Domain (

min <- s.min,

max <- s.max

)

}

The Feature2Variable rule takes each

source feature and transforms it into a variable. In

the modus operandi of this rule, the feature’s name

is affected to the variable’s name and the

haveDomain variables’ relationship is the

collection of the haveCardinality features’

relationship. If the feature to be transformed has a

ENASE 2011 - 6th International Conference on Evaluation of Novel Software Approaches to Software Engineering

194

cardinality, then the subordinated rule (lazy rule)

Cardinality2Domain is called to represent the

correspondig cardinality as a domain of the feature.

While ATL generates XMI files we are still not

at a level of an exploitable specification. To be

exploitable, the XMI files must be transformed into

a file that can be interpreted by a constraint solver,

in our case GNU-Prolog, but we encourage the use

other solvers and compare the results obtained from

them as part of a future work. In our approach, this

is achieved by means of XPath queries over the

resulted XMI file. This approach is completely

automated by means of our Eclipse plug-in

VariaMos (Mazo, 2010). VariaMos creates a new

file that contains a GNU-Prolog program embedding

the XMI file. The new CP representation of the FM

is then ready to be executed and analysed by the

GNU Prolog solver using a series of operations that

can be passed dynamically to the solver. A snapshot

of the VariaMos interface to translate FMs into CPs

is presented in Figure 3.

Figure 3: Graphical user interface to transform FMs into

constraint programs.

4.2 Scalability

Both transformation strategies were tested in a

laptop computer with Windows vista 32 bits and

with the following characteristics: processor AMD

Turion(tm) X2 Dual-Core Mobile RM-74 of 2,20

MHz and 4,00 GB of RAM.

4.2.1 Transformation using the Navigation

API Strategy

Table 1 shows the average results of our experiment.

These results show that our transformation rules can

be executed in a fast and interactive way by using a

well known API to navigate on FMs.

Table 1: Average time to transform FMs into CPs using

SPLOT.

Number of features Time to transform FMs into CPs

<40 < 1sec

40 to 100 1 sec

101 to 500 1,5 sec

1000 2 sec

2000 3,5 sec

5000 16 sec

10000 70 sec

4.2.2 Transformation using the Engine

Transformation Strategy

Table 2 reports the average time of our experiment.

These figures show that, even for the largest

industrial models considered, our proposal is

scalable and interactive for an engineer in a normal

work environment (no need of additional hardware

or software resources)

Table 2: Average time to transform FMs into CPs using

ATL engine.

Number of

features

Time to transform

FMs into XMI CPs

Time to transform

XMI CPs into

Text CPs

<50 <1 sec < 1sec

50 to 100 3sec <1 sec

101 to 150 5sec 1sec

152 to 180 6,5 sec 1 sec

4.3 Usability

Once the 48 FMS transformed into Benavides et

al.’s (2005), (2005b) and our CP representations, we

executed a series of reasoning operations on these

models. These operations were executed in our

VariaMos tool. The results show an average

reduction of 45% in the execution time of derivation

(e.g., find a product that satisfies given configuration

requirements), verification (e.g., find dead features

and void FMs) and analysis operations (e.g., find the

number of products). Figure 4 shows a time

comparison needed to get a product from a FM

transformed to a CP using both proposals. In Figure

4, we use a log scale to distribute the number of

features (X axis) in order to avoid overlapping of

results on models from 10 to 100 features. This

figure indicates that for the same study conditions

there our transformation rules seem to have a better

performance.

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

195

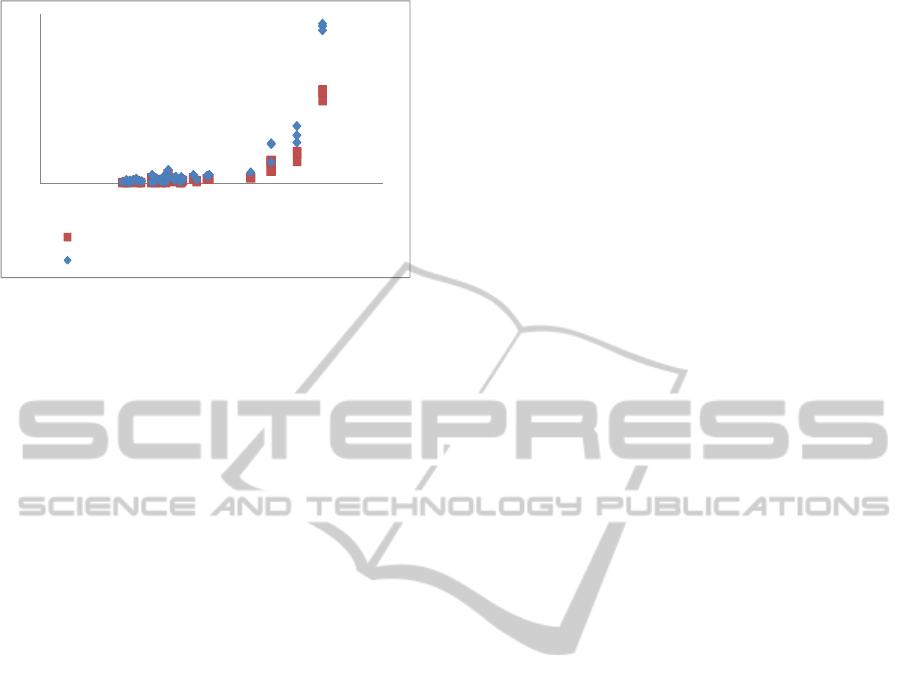
Figure 4: Time (in milliseconds) needed to obtain a

product from a FM. 48 FMs up to 2000 features,

transformed to CP formulas using existing rules and ours.

Finally our approach was also compared to

Karataş’s one (Karataş et al., 2010). Of course, to

perform this comparison, we had to correct the error

we identified in Karataş’ algorithm in order to

preserve the semantic of FMs. This change was

necessary to ensure that both representations were

totally equivalent, by representing the same products

from each FM. Each one of the 12 FMs transformed

in both representations was analyzed using

VariaMos tool. As result of our experiment we have

a benefit of average 58% in the execution time of

each configuration operation –see section 2.3. This

gain is due to the fact that in our representation

algorithm we avoid the combinatorial explosion on

group cardinalities, exclusive relationships and

additional constraints, by using arithmetic

operations. For instance, to constrain the use of only

one feature, among A, B and C in a product, we use

the expression A+B+C=1 instead of: (¬A˄¬B˄C)

∨ (¬A˄B˄¬C) ∨ (A˄¬B˄¬C). And, in the kind

of solver we are using, a CP over integer domain

solver, the first formula is executed faster than the

second one.

4.4 Correctness

The approach that we present in this paper was

compared with the transformation algorithm of

Benavides et al. (2005b). We tested the correctness

of our approach by means of two experiments. The

first one consists in comparing the number of

products that could be derived from our collection of

FMs represented with Benavides’ rules and the rules

presented in this paper. In both cases, the number of

products was equal. The second one consisted in

taking 3 models randomly, manually derive all the

possible products from the FM, then compare these

results with the results obtained using VariaMos. For

practical reasons, we only considered models with

less than 50 features from our initial sample. It is

worth noting that in our comparison we checked, by

manual inspection, that not only the numbers of

products, but also the products themselves, were the

same. These results allow us to conclude that our CP

representation of FMs preserves the semantic of

models. It should be noticed that in our approach,

the structure of FMs is not preserved because it is

not necessary for the 11 reasoning operations that

we execute on FMs (better explained in section 2.3).

Nevertheless, we consider study the impact of FMs’

structure on other kind of eventual reasoning

operations and if some exist we encourage in future

works to represent FMs preserving also their

structure.

5 RELATED WORKS AND

DISCUSSION

Benavides et al. (2005b) present an algorithm to

transform a FODA model into a CP. They suggest

considering four aspects during the mapping a feature

model into a constraint program: (i) the features make

up the set of variables; (ii)

the domain of each

variable is the same: {true, false}; (iii) extra–

functional features are expressed as constraints; and

(iv) every relation of the feature model becomes a

constraint among its features. Benavides (Benavides,

2007) extended their previous work to reason about

constraints specified on feature attributes. Constraints

such as F1.A = F2.B + F3.C can be specified

to express that in any configuration, the value of

attribute A associated with feature F1 should be equal

to B+C where B and C are attributes respectively

associated to F2 and F3. This allows to reason on

extra functional features as defined by Czarnecki et

al. (2005), i.e. relations between one or more

attributes of one or different features. Item (ii) shows

that Benavides’ proposal is a Boolean-based

approach, which limits the use of Integer constraints

(i.e., cardinalities [min..max], where min and

max are integer values and not only limited to 0 or 1).

In addition, their work is limited to FODA-like

models and not pretend to analyse a systems

represented through several model views. Thanks to

our approach it is possible to integrate different views

of the PL in a global model and then analyse it

because in CP, constraints representing different

views can be integrated without a specific order and

the domain of variables is considered as

100

150

200

250

300

350

400

1 10 100 1000 10000

Time to have a product with our transformation rules

Time to have a product with Benavides' tranformation rules

log

N°features

time

(ms)

ENASE 2011 - 6th International Conference on Evaluation of Novel Software Approaches to Software Engineering

196

supplementary constraints. Views integration and

analysis are out of scope of this paper.

Van Deursen and Klint (2002) proposes to reason

on feature models by translating them into a logic

program using predicates such as all( ), one-

of( ), or more-of(), that respectively specify

mandatory, mutually exclusive, and alternative

features. For instance constraints: F1 = all

(F2, F3, F4), F4 = one-of (F5, F6)

specify that if F1 is included in a configuration, then

F2, F3, and F4, and therefore either F5 or F6

should be included too. The use of CP to reason

about feature model was extended by Batory [2],

who proposes an approach to transform a feature

model into propositional formula using the ∧, ∨, ¬,

⇒ and ⇔ operations of propositional logic. This

enables for example constraints of the form F ⇒ A ∨

B ∨ C meaning that feature F needs features A or B

or C, or any combination thereof. As in (Van

Deursen and Klint, 2002), in these constraints,

features are Boolean variables (either they are

included or not in a configuration). Thus, our

approach not also deals with Boolean constraints but

also Arithmetic constraints, Symbolic constraints

and Reified constraints over finite-domain variables.

Integer CP allows us to execute requirements as:

“the value of attribute F1.A should always be equal

to F2.B + F3.C” to control the value of integer

feature attributes, as proposed by (Benavides, 2007).

As well as to control the number of occurrences of a

feature, as for instance in the constraint “a product

should include at least 2 and at most 4 occurrences

of feature F”. Feature cardinalities were proposed

by Czarnecki et al. (2005), but constraint analysis on

feature cardinalities has not yet been tackled to our

knowledge (Benavides et al., 2010), and there is no

tool available so far to support the analysis of

constraints on feature cardinalities and on feature

attributes in an integrated way. Finite domain

constraints can also apply on any ENUM PL

properties, like in the Decision King tool which uses

them to control decision consistency (Dhungana et

al., 2007). CP also enables the specification of

“complex” product requirements (complex

compared to select or not a feature) under the form

of additional constraints specified during the

configuration. For example, our approach supports

the specification of constraints such as “provide me

with all possible configurations in which the value of

feature attributes A1..Ai is in [a..b]”. This is useful

in staged configuration (Djebbi and Salinesi, 2007).

Other new kinds of product-specific constraints such

as: “provide with a configuration in which the

values of all the attributes associated with features

F1..Fn are different from each other”, and “provide

me with all product configurations in which features

F1...Fn are either all included or all excluded” or

“provide me with the features that have not the

chance to be selected (dead features)”. Such

constraints can be used to query the PL model, that

is useful for instance to explore configuration

scenarios, or in a verification activity.

Recent work by Karataş et al. (2010) proposes a

transformation from extended feature models to CP.

This work considers neither the actual semantic of

features’ attributes, as it considers them as sub-

features that can be selected or not, nor the semantic

of cardinality-based feature models as it was

validated by the community (Michel et al., 2011).

Our work goes a step further by testing our

transformation patterns on the most complete set of

feature models publicly available. Additionally, the

transformation patterns used by Karataş considers

only boolean formulas to represent extended feature

models, which reduces the richness of the constraint

programming paradigm, a richness that we believe is

necessary to represent complex feature models and

to support advanced reasoning (e.g. to detect the

optimal product according to a cost criterion).

Besides, we detected an error in their CP

representation regarding optional features. Karataş et

al.’s representation of optional features allows

selection of child features without constraining the

selection of the father feature.

6 CONCLUSIONS AND FUTURE

WORK

In this paper we provide an approach to transform

FMs with attributes and feature cardinalities into

constraint programs. To our knowledge, it is the first

time that a proved representation of these kinds of

models is presented. Once our 60 FMs represented

as constraint programs, we applied on them our

collection of 11 reasoning operations, completely

automated in our tool VariaMos and the CP solver

GNU-Prolog (Diaz and Codognet, 2001). We use

GNU-Prolog to reason on FMs, but other solver can

be used as another alternative. Even if GNU-Prolog

is not the best solver to implement some reasoning

operations on very large models (e.g. to calculate the

number of products or to list all the products of a

FM), it performed well and showed an excellent tool

for other kind of reasoning (e.g. determining if a FM

is void or not, to find dead features, false optional

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

197

features, non attainable domains of a variable or in

the case of configuration with and without extra-

requirements).

As future work, we are considering, in one hand, to

work on other type of reasoning operations on

product line models. And on the other hand, we

propose an experimental design to evaluate the

performance, memory consumption and precision of

these operation when we implement then in different

solvers (SAT, CSP, CLP, BDD, ADD, etc.).

Additionally, we propose to work in multidirectional

transformation, because our up-to date work only

considers unidirectional transformations.

REFERENCES

Batory, D. S., 2005. Feature models, grammars, and

propositional formulae. In: 9th International Software

Product Lines Conference, pp. 7–20. Springer.

Benavides, D., 2007. On the Automated Analysis of

Software Product Lines Using Feature Models. A

Framework for Developing Automated Tool Support.

University of Seville, Spain, PhD Thesis.

Benavides, D., Ruiz-Cortés, A., Trinidad, P., 2005. Using

constraint programming to reason on feature models.

In: The Seventeenth International Conference on

Software Engineering and Knowledge Engineering,

SEKE 2005, pp. 677–682.

Benavides D., Segura S., Ruiz-Cortés A., 2010.

Automated Analysis of Feature Models 20 Years

Later: A Literature Review. Information Systems.

Elsevier.

Benavides, D., Trinidad, P., Ruiz-Cortés, A, 2005.

Automated Reasoning on Feature Models. In: Pastor,

Ó., Falcão e Cunha, J. (eds.) CAiSE 2005. LNCS, vol.

3520, pp. 491–503. Springer, Heidelberg.

Bessiere, Ch., 2006. Constraint propagation. In Francesca

Rossi, Peter van Beek, and Toby Walsh, editors,

Handbook of Constraint Programming, pages 29–83.

Elsevier.

Czarnecki, K., Helsen, S., Eisenecker, U., 2005.

Formalizing cardinality-based feature models and their

specialization. Software Process: Improvement and

Practice, 10(1):7– 29.

Dhungana, D., Heymans, P., and Rabiser, R., 2010. A

Formal Semantics for Decision-oriented Variability

Modeling with DOPLER, Proc. of the 4th

International Workshop on Variability Modelling of

Software-intensive Systems (VaMoS 2010), Linz,

Austria, ICB-Research Report No. 37, University of

Duisburg Essen, pp. 29-35.

Dhungana, D., Gruenbacher, P., Rabiser, R., 2007.

DecisionKing: A Flexible and Extensible Tool for

Integrated Variability Modeling. In: 1rst Int.

Workshop VaMoS, pp120-128, Ireland.

Diaz, D., Codognet, P., 2001. Design and Implementation

of the GNU Prolog System. Journal of Functional and

Logic Programming. http://www.gprolog.org.

Djebbi, O., Salinesi, C., 2007. RED-PL, a Method for

Deriving Product Requirements from a Product Line

Requirements Model. In: CAISE’07, Norway.

Gurp, J. v., Bosch, J., Svahnberg, M., 2001. On the Notion

of Variability in Software Product Lines. In

Proceedings of the Working IEEE/IFIP Conference on

Software Architecture (WICSA).

Halmans, G., Pohl, K., 2003. Communicating the

variability of a software-product family to customers.

Softw Syst Model. 2: 15–36 / Digital Object Identifier

(DOI) 10.1007/s10270-003-0019-9.

Kang, K., Cohen, S., Hess, J., Novak, W., Peterson, S.,

1990. Feature-Oriented Domain Analysis (FODA)

Feasibility Study. Technical Report CMU/SEI-90-TR-

21, SEI, Carnegie Mellon University.

Kang, K., Lee, K., Lee, J., 2002. FOPLE - Feature

Oriented Product Line Software Engineering:

Principles and Guidelines. Pohang University of

Science and Technology.

Karataş A. S, Oğuztüzün H., Do

ğru A., 2010. Mapping

Extended Feature Models to Constraint Logic

Programming over Finite Domains. SPLC, Korea.

Mazo, R., 2010. VariaMos Eclipse plug-in: https://

sites.google.com/site/raulmazo/

Mazo, R., Grünbacher, P., Heider, W., Rabiser, R.,

Salinesi, C., Diaz, D., 2011. Using Constraint

Programming to Verify DOPLER Variability Models.

5th ACM International Workshop on Variability

Modelling of Software-intensive Systems (VaMos'11),

Namur-Belgium.

Mazo R., Lopez-Herrejon R., Salinesi C., Diaz D., Egyed

A., 2011. A Constraint Programming Approach for

Checking Conformance in Feature Models. In 35th

IEEE Annual International Computer Software and

Applications Conference (Compsac'11). Munich-

Germany.

Mendonça, M., Branco, M., Cowan, D., 2009. S.P.L.O.T.:

software product lines online tools. In OOPSLA

Companion. ACM, http://www.splot-research.org.

Mendonça, M., Wasowski, A., Czarnecki, K., 2009. SAT–

based analysis of feature models is easy. In

Proceedings of the Sofware Product Line Conference.

Michel, R., Classen, A., Hubaux, A., Boucher, Q., 2011. A

Formal Semantics for Feature Cardinalities in Feature

Diagrams. 5th International Workshop on Variability

Modelling of Software-intensive Systems (VaMos'11),

Namur-Belgium.

Nuseibeh, B. Easterbrook, S., 2000. Requirements

Engineering: A Roadmap, The Future of Software

Engineering, 22nd Int. Conf. on Soft. Eng., 37-46,

ACM, Washington.

Salinesi, C., Mazo, R., Diaz, D., 2010. Criteria for the

verification of feature models, In 28th INFORSID

Conference, Marseille, France.

Salinesi, C., Mazo, R., Diaz, D., Djebbi, O., 2010b.

Solving Integer Constraint in Reuse Based

Requirements Engineering. 18th IEEE International

Conference on Requirements Engineering (RE'10).

Sydney, Australia.

ENASE 2011 - 6th International Conference on Evaluation of Novel Software Approaches to Software Engineering

198

Salinesi C., Mazo R., Djebbi O., Diaz D., Lora-Michiels

A, 2011. Constraints: the Core of Product Line

Engineering. Fifth IEEE International Conference on

Research Challenges in Information Science (IEEE

RCIS), Guadeloupe-French West Indies, France.

Schobbens, P. Heymans, P. Trigaux, J. Bontemps, Y.,

2007. Generic semantics of feature diagrams, Journal

of Computer Networks, Vol 51, Number 2.

Schulte, Ch., Stuckey., P. J., 2008. Efficient constraint

propagation engines. ACM Trans. Program. Lang.

Syst., 31(1).

Streitferdt, D., 2004. FORE Family-Oriented

Requirements Engineering, PhD Thesis, Technical

University Ilmenau.

Van Hentenryck, P., 1989. Constraint Satisfaction in

Logic Programming. The MIT Press.

Van Deursen, A., Klint, P., 2002. Domain–specific

language design requires feature descriptions. Journal

of Computing and Information Technology, Vol. 10,

No. 1.

Ziadi, T., Helouet, L., Jezequel, J.-M., 2003. Towards a

UML Profile for Software Product Lines. In: Software

Product- Family Engineering, 5th International

Workshop, pages 129– 139. Springer.

TRANSFORMING ATTRIBUTE AND CLONE-ENABLED FEATURE MODELS INTO CONSTRAINT PROGRAMS

OVER FINITE DOMAINS

199