A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC
MONTGOMERY ARCHITECTURE
Zongbin Liu
1
, Luning Xia
1
, Jiwu Jing
1
and Peng Liu
2
1
The State Key Laboratory of Information Security, Graduate University of Chinese Academy of Sciences, Beijing, China
2
The Pennsylvania State University, University Park, Pennsylvania, U.S.A.
Keywords:
Montgomery, RSA, FPGA.
Abstract:
In this paper we propose a new hardware architecture of modular exponentiation, which is based on the op-
timized Montgomery multiplication. At CHES 1999, Tenca introduced a new architecture for implementing
the Montgomery multiplication which was later improved by Huang
et al. at PKC 2008. In this paper we
improve the architecture of Huang and the improved one occupies less hardware resource, at the same time
we add the final subtraction of the Montgomery algorithm into the architecture in order to do the exponentia-
tion computation. Finally we use this improved architecture to build a RSA coprocessor. Compared with the
previous work, the new 1024-bit RSA coprocessor saved nearly 50% of area, and the area utilization is greatly
improved. This design is the smallest design as we know in the literature, and we verified the correctness by
huge test data.
1 INTRODUCTION
As the RSA algorithm is secure and easy to imple-
ment, it is the most widely used public key cryptosys-
tem. The performance of the RSA scheme is primar-
ily determined by an efficient implementation of the
modular arithmetic. Because computation of modular
multiplication is intense, processing this algorithm re-
quires a huge amount of computation, therefore var-
ious algorithms for speeding up modular multiplica-
tion have been proposed in the literature. Among
them the Montgomery multiplication algorithm is the
most efficient modular multiplication algorithm. The
Montgomery method is based on an ingenious repre-
sentation of the residue class modulo M, and replaces
division by M with division by a power of 2, which
can be easily accomplished since numbers are repre-
sented in binary form on a computer.
Although the Montgomery algorithm is efficient,
its software implementations are still not quick
enough (for SOC (system on chip)). To address this
problem, many architectures have been proposed to
speed up the Montgomery algorithm on hardware. At
CHES 1999, Tenca
et al. (Tenca and Koc¸, 1999) pro-
posed a scalable architecture for Montgomery mul-
tiplication. In their architecture, it performs a sin-
gle Montgomery multiplication in approximately 2n
clock cycles, where n is the size of operands in bits.
At PKC 2008, Huang
et al. proposed a novel archi-
tecture to improve the architecture of Tenca. The new
architecture performs a single Montgomery multipli-
cation in approximately n clock cycles. However, nei-
ther the architecture of Tenca nor the architecture of
Huang has implemented the final subtraction of the
Montgomery algorithm, because their architecture is
used for assisting software to speed up modular mul-
tiplication, and subtraction can be done outside the
modular multiplication module, such as software can
do the subtraction. If we want implement modular
exponentiation in hardware, we must implement the
whole Montgomery algorithm. Since the last step of
the Montgomery algorithm is a n-bit size subtraction,
where n is the size of operands in bits, this path is a
long path in implementingthe Montgomery algorithm
in modular exponentiation, here critical path denotes
the longest combination circuit. What’s more, this ex-
tra step will use huge FPGA resources because the
key size is very big.
Nowadays, the cryptographic algorithm is used
in many SOC( System on Chip ) designs, but the
CPU computation capacity in the SOC design is not
enough to implement high speed cryptographic al-
gorithm. Thus the cryptographic module is neces-
sary to speed up cryptographic algorithm computa-
tion. However,cryptographic module which is not the
main function module usually occupies only a small
105
Liu Z., Xia L., Jing J. and Liu P..
A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC MONTGOMERY ARCHITECTURE.
DOI: 10.5220/0003511401050113
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 105-113
ISBN: 978-989-8425-71-3
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

part of the SOC design area, so the area of crypto-
graphic module must be constricted to certain size.
The smaller the cryptographic module is, the better.
If the resources consumption is too big, the cost as an
important indicator of the SOC design will increase
too much, especially in the commercial SOC design.
From this aspect, the resources consumption of the
cryptographic hardware design is a very significant
indicator in hardware implementation, and good de-
sign can make cryptographic algorithm using in many
more application areas.
In this paper we improve the architecture of
Huang by adjusting the inner architecture of the pro-
cess elements, in such a way that Montgomery mul-
tiplication consumes fewer resources. Moreover our
architecture also adds the final subtraction( of the
Montgomery algorithm ) but doesn’t require addi-
tional clock cycles and the area is smaller as com-
pared to the architecture of Huang. Based on this
novel Montgomery multiplier, we implemented a new
RSA coprocessor which compared with the previous
work (Shieh et al., 2008) saved nearly 50% of slices,
what’s more, this is the smallest design as we know
in the literature at present. This new module has been
used into our other SOC designs, it works well, it is
a very useful cryptographic module in practical SOC
design.
The rest of the paper is organized as follows. Sec-
tion 2 reviews the preliminary of RSA and Mont-
gomery. Section 3 proposes an improved architecture
of the Montgomery algorithm. Section 4 presents the
architecture of our RSA coprocessor. Section 5 shows
an evaluation, analysis and comparison of our work
and some related works in the literature. The last sec-
tion concludes the whole paper.
2 PRELIMINARIES
2.1 Preliminaries: RSA Algorithm
RSA algorithm is a public-key encryption algorithm
that is used to develop a cryptosystem that offers both
public key encryption and digital signatures (authen-
tication) (Kaya-Koc, 1995). The algorithm is named
after three MIT mathematicians, Rivest, Shamir and
Adleman, who invented it in 1978, and its security
lies in the difficulty of factoring large integers. In the
RSA algorithm, the basic operation is modular expo-
nentiation of large integers. The parameters are n, p
and q, e, and d. The modulus n is the product of dis-
tinct large random primes: n = pq. The public ex-
ponent e is a number in the range 1 < e < φ(n) such
that gcd(e,φ(n)) = 1, where φ(n) is Euler function
of n, given by φ(n) = (p − 1)(q − 1). The private
exponent d is obtained by inverting e modulo φ(n).
d = e
−1
modφ(n), by using the extended Euclidean
algorithm we can get d. The encryption operation is
performed by computing C = M
e
(mod n), where M
is the plain text such that 0 ≤ M < n. The number
computing is the cipher text from which the plain text
M can be computed using M = C
d
(mod n). The RSA
algorithm can be used in many areas, such as sending
encryption messages and producing digital signature
for electronic message.
The modular exponentiation operation is the most
important operation in the RSA algorithm. In paper
(Kaya-Koc, 1995), the author reviewed the modular
exponentiation operation implemented on hardware.
This paper showsthat there are mainly two methods to
complete modular exponentiation, which are LR Bi-
nary Method and RL Binary Method.
Algorithm 1: LR Binary Method.
Input: M, e, n
Output: C := M
e
mod n
1 begin
2 if e
h−1
= 1 then
3 C := M;
4 else
5 C := 1;
6 for i = h− 2 to 0 do
7 C := C·C(mod n) ;
8 if e
i
= 1 then
9 C := C · M(mod n) ;
10 return C;
In Algorithm 1, exponent e is scanned from
the most significant bit(MSB) to the least signif-
icant(LSB). In the scanning process, the modular
squaring is performed for each bit, but the modular
multiplication is only performed when bit is 1. In the
LR Binary Method the squaring and multiplying op-
erations must be performed sequentially. This algo-
rithm takes 2h multiplications in the worst case con-
dition and 1.5h multiplications on average to com-
plete modular exponentiation since the multiplication
doesn’t need to compute when e
i
= 0, where h is the
size of operands e in bits. This implies that only a
single hardware multiplier is needed to perform the
squaring and multiplying. The cryptographic mod-
ule can not consume more hardware resources since
in some designing conditions, such as SOC, there are
many modules on the same chip and the hardware re-
sources is limited.
The RL Binary Method is another method to com-
plete modular exponentiation. Compared with the LR
Binary Method, this method can speed up the expo-
nentiation operation, however, it needs another modu-
SECRYPT 2011 - International Conference on Security and Cryptography
106

Algorithm 2: RL Binary Method.
Input: M, e, n
Output: C := M
e
mod n
1 begin
2 C := 1 ;
3 P := M;
4 for i = 0 to h− 2 do
5 if e
i
= 1 then
6 C := C· P(mod n) ;
7 P := P· P(mod n) ;
8 if e
h−1
= 1 then
9 C := C· P(mod n) ;
10 return C;
lar multiplier. In the RL Binary Method, the squaring
and multiplying operations are independent of each
other and can be executed in parallel to achieve a
2-fold speed-up. However, two hardware multipli-
ers are required to achieve this speed-up in the ar-
chitecture based on this algorithm. Comparing the
two algorithms above, the LR Binary Method al-
lows the square and multiplication operations to exe-
cute sequentially, but the RL Binary Method executes
the square and multiplication parallelly. Using this
method the RL Binary Method can reduce the com-
putation time. However, the RL Binary Method needs
an extra Montgomery multiplier and consumes more
hardware resources, because the Montgomery multi-
plier consumes a huge hardware resources.
2.2 Preliminaries: Montgomery
Algorithm
The algorithm for modular multiplication described
below has been proposed by P.L. Montgomery in
1985 (Montgomery, 1985). The algorithm is consid-
ered to be the fastest algorithm to compute AB mod
M in computers when the values of A,B and M are
large. It is a method for multiplying two integer mod-
ulo M, while avoiding division by M. Paper (Harris
et al., 2005) reviewed the Montgomery algorithm and
gave two modified version. The following part gives
a brief description of the Montgomery algorithm.
When we want to compute AB mod M in a com-
puter. First, let the modulus M be a k−bit integer, i.e.,
2
k−1
≤ M < 2
k
, and let R be 2
k
. The Montgomery
multiplication algorithm requires that R and M be
relatively prime, i.e., gcd(R,M) = gcd(2
k
,M) = 1.
This requirement is satisfied if M is odd. In or-
der to describe the Montgomery multiplication, we
first define the M-residue of an integer A < M as
¯
A = A· R(mod M). It is straightforward to show that
the set {A· R(mod M)|0 ≤ A ≤ M − 1} is a complete
residue system. Thus, there is one-to-one correspon-
dence between the numbers in the range 0 and M − 1
and the numbers in the above set. The Montgomery
reduction algorithm exploits this property by intro-
ducing a much faster multiplication routine which
computes the M-residue of the product of the two in-
tegers whose M-residues are given. Given two M-
residues
¯
A and
¯
B, the Montgomery product is defined
as the M-residue
¯
C =
¯
A·
¯
B· R
−1
(mod M) where R
−1
is the inverse of R modulo M, i.e., it is the number
with the property R
−1
·R = 1(mod M). In order to de-
scribe the Montgomery reduction algorithm, we need
an additional quantity, M
′
, which is the integer with
the property RR
−1
− MM
′
= 1. The R
−1
and M
′
can
both be computed by the extended Euclidean algo-
rithm. The computation of Mon(
¯
A,
¯
B) is achieved by
algorithm 3:
Algorithm 3: Montgomery.
Input:
¯
A,
¯
B
Output: Mon(
¯
A,
¯
B)
1 begin
2 T :=
¯
A·
¯
B;
3 U := (T + (T · M
′
mod R) · M)/R;
4 if U ≥ M then
5 then return U − M
6 else
7 return U
Because R is a power of 2, multiplication modulo
R and division by R are both intrinsically fast opera-
tions both in hardware and software application envi-
ronment. Thus the Montgomery product algorithm is
potentially faster and simpler than ordinary computa-
tion of A· BmodM, which involves division by M. So
Montgomery algorithm is used in many algorithms to
speed up modular multiplication.
After the Montgomery was proposed, there are
many methods implementing this algorithm on hard-
ware. The potential difficulty in the Montgomery
algorithm implementation is the addition of long
operands. Various designs toward relaxing the prob-
lem of long carry propagation fall into two categories.
In the first approach, the intermediate results are kept
in carry-saveform to avoid carry propagation(Cilardo
et al., 2004) (Mclvor et al., 2003). Another approach
is based on systolic architecture, which is firstly pro-
posed by Tenca et al. (Tenca and Koc¸, 1999) at
CHESS 99. Their Montgomery multiplier architec-
ture is a scalable architecture, which is based on the
Multiple Word Radix-2 Montgomery Multiplication
Algorithm(MWR2MM). In Algorithm 4, the operand
Y (multiplicand) is scanned word by word, and the
operand X (multiplier) is scanned bit-by-bit. In the
algorithm, it uses the following vectors:
M = (M
e−1
,· · · · M
1
,M
0
) (1)
A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC MONTGOMERY ARCHITECTURE
107

Algorithm 4: The MWR2MM Algorithm.
Input: odd M, n = ⌊log
2
M⌋ + 1, word size w,
e = ⌈
n+1
w
⌉, X =
∑
n−1
i=0
x
i
· 2
i
,
Y =
∑
e−1
j=0
Y
( j)
· 2
w· j
, M =
∑
e−1
j=0
M
( j)
· 2
w· j
,
with 0 ≤ X,Y < M
Output: Z = X ·Y · 2
−n
mod n
1 begin
2 S = 0 ;
3 for i = 0 to n− 1 do
4 (C,S
(0)
) := x
i
Y
(0)
+ S
(0)
;
5 if S
(0)
0
= 1 then
6 (C,S
(0)
) := (C, S
(0)
) + M
(0)
;
7 for j = 1toe− 1 do
8 (C,S
( j)
) :=C+S
( j)
+M
( j)
+x
i
Y
( j)
;
9 S
( j−1)
:= (S
( j)
0
,S
( j−1)
w−1...1
);
10 S
( j−1)
:= (S
( j−1)
0
,S
(e−1)
w−1...1
);
11 else
12 for j = 1toe− 1 do
13 (C,S
( j)
) := C+ S
( j)
+ x
i
Y
( j)
;
14 S
( j−1)
:= (S
( j)
0
,S
( j−1)
w−1...1
);
15 S
( j−1)
:= (S
( j−1)
0
,S
(e−1)
w−1...1
);
Y = (Y
e−1
,· · · ·Y
1
,Y
0
) (2)
X = (x
m−1
,· · · · x
1
,x
0
) (3)
3 OPTIMIZING MONTGOMERY
ARCHITECTURE
This section presents a detail description of our novel
Montgomery multiplier architecture. At PKC 2008,
Huang (Huang et al., 2008) proposed an optimized
Montgomery architecture based on the work of Tenca
(Tenca and Koc¸, 1999), compared with the archi-
tecture of Tenca, the optimized architecture used
less clock cycles to complete modular multiplication.
However, neither the architecture of Tenca nor the ar-
chitecture of Huang has implemented the final sub-
traction of the Montgomery algorithm, the author ex-
plained that the subtraction can be calculated out-
side the module. But if we we want implement the
the whole exponentiation calculation in hardware, we
must design a method to implement the last subtrac-
tion. Since the key size in RSA is very big, a small
change of the architecture will consume huge FPGA
resources, we must improve the architecture of Huang
making it more suitable to compute exponentiation in
hardware directly. In this research we improved the
architecture of Huang, by fixing the inner architec-
ture of the PE and the control logic, by such a way
that Montgomery multiplication consumes fewer re-
sources comparing to Huang’s work. Moreover our
architecture also adds the final subtraction( of the
Montgomery algorithm ) but doesn’t require addi-
tional clock cycles as compared to the architecture
of Huang, what’s more our design is smaller than
Huang’s work. We implement a new RSA coproces-
sor based on this novel Montgomery multiplier, com-
pared with the previous work (Shieh et al., 2008) the
new coprocessor can save nearly 50% of slices and
this one is the smallest one as we know at present. The
new architecture of Montgomery multiplier has four
types processing element(PE) unit, the architecture
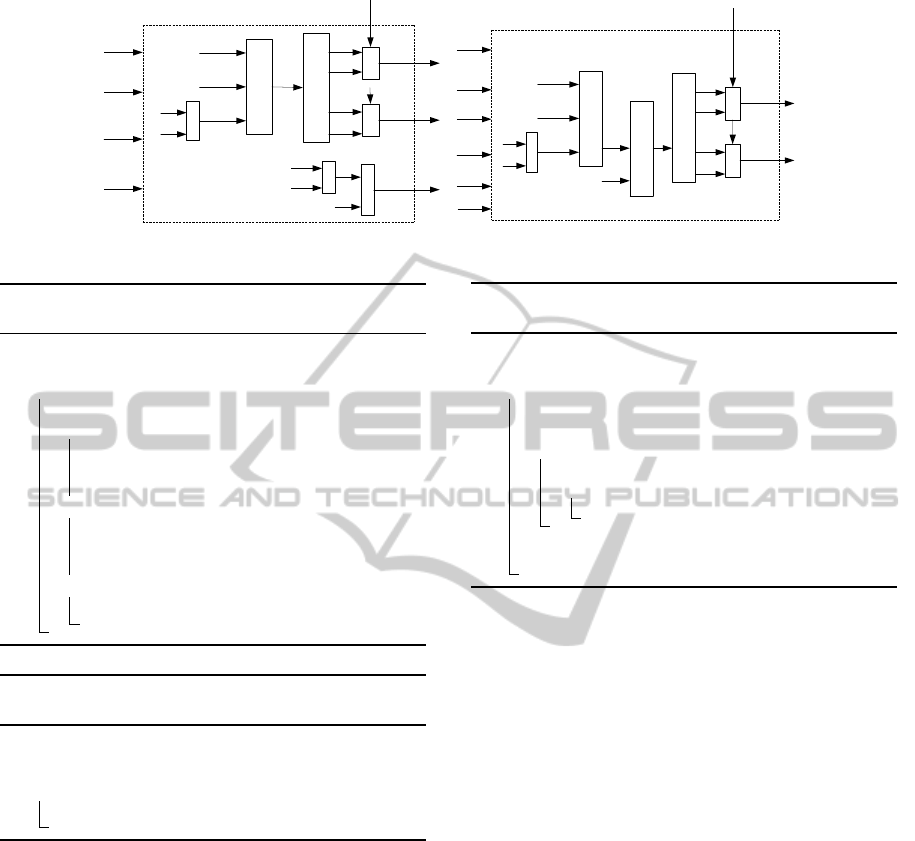
of the four types PE is respectively showed in Fig.2,
Fig.3. Compared with the architecture of Huang, we
change the internal architecture and control unit to
save resources and add one extra PE to complete the
final subtraction of Montgomery algorithm. In this ar-
chitecture, the multiplier x
i
is loaded bit serially from
the LSB of the register, and uses the shift register to
load into PE, at the same time, the control signal is
also loaded by the shift register into every PE. Fig.1
shows the new architecture of the Montgomery mul-
tiplier.
After n clock cycles, the LSB of the result S
0
is
valid at the LSB and after further e clocks cycles, the
MSB of the result is valid. The difference between
our architecture and Huang’s architecture is that, after
n clock cycles, the PE#S completes the S− M, after e
clock cycles the S − M and S are all ready, at last the
final result of the modular multiplication can be got
by the carry bit.
Algorithm 5 is the new pseudo code of PE#F. The
left of Fig.2 shows the improved architecture of this
PE. In the architecture of this PE, the carry save adder
(CSA) can speed up the addition operation and save
logic resources. In traditional, the CSA used to finish
long adder, here we use CSA in this PE, because CSA
can compress the addition time, what’s more control
signal and adder can use the FPGA resources effec-
tively, since in the new FPGA, the LUT is six inputs,
one LUT can finish this one bit addition and the con-
trol flow. The Control signal presents the state regis-
ter, the control signal is 2-bit width, so control register
can generate four states to control the PEs to complete
the computation. In first state, the PE unit completes
the addition; in the second state, the PE unit keeps the
intermediate results and locks the S
(i+1)
0
; in the other
states, PE keeps all the intermediate results in order
to complete the final subtraction, and outputs the last
result. q
i
is also controlled by the Control signal, be-
cause in the last loop and the subtraction loop of Al-
gorithm 4, q
i
should be zero.
Algorithm 6 is the pseudo code of PE#E, two level
SECRYPT 2011 - International Conference on Security and Cryptography
108

















 !
 !
 !

6
L
6
 −H
6

6
 −H
6

VXE
6
 −H
VXE
6

<

<

<
L
<

0

0

0
L
0

0



6

VXE
6

0
 −H
0

F

F
−H
F
"
H
F
L
[
−L
[
−L
[
ML
[
−

6

6


6

&


6
!

6

&
!
&
 M
&


M
6


−H
6
 −H
&
"
"
 +M
&
L
T
 −L
T
−L
T
ML
T
−


+M
6
"
"
Figure 1: The architecture of Montgomery Multiplier.
Algorithm 5: Pseudocode of processing element of
type F.
Input: x
i
,Y
(0)
,M
(0)
,S
(1)
0
,Control
Output: C
(1)
,S
(0)
,q
i
1 begin
2 S
temp
= 0 ;
3 q
i
= ((x
i
·Y
(0)
0
) ⊕ S
(0)
0
)&Control
0
;
4 if Control == St1 then
5 CO
1
,SO
(0)
,S
(0)
w−2...1
=
(1,S
(0)
w−1...1
+ x
i
·Y
(0)
+ q
i
· M
(0)
);
6 CE
1
,SE
(0)
,S
(0)
w−2...1
=
(0,S
(0)
w−1...1
+ x
i
·Y
(0)
+ q
i
· M
(0)
);
7 else if Control == St2 then
8 S
temp
= S
(1)
0
;
9 (CO
(1)
,SO
(0)
,S
(0)
w−2...1
) =
(CO
1
,SO
(0)
,S
( j)
w−2...1
) ;
10 (CE
(1)
,SE
(0)
) = (CE
1
,SE
(0)
) ;
11 else
12 (CO
(1)
,SO
(0)
,S
(0)
w−2...1
) =
(CO
(1)
,SO
(0)
,S
(0)
w−2...1
) ;
13 (CE
(1)
,SE
(0)
) = (CE
(1)
,SE
(0)
) ;
14 S
temp
= S
temp
15 S
(0)
=
(S
temp
) ? (SO
(0)
,S
(0)
w−2...1
) : (SE
(0)
,S
(0)
w−2...1
) ;
16 C
(1)
= (S
temp
) ? CO
(1)
:CE
(1)
;
CSA can be used to speed up the addition. The right
side of Fig.2 shows the architecture of this improved
PE. As the same as PE#F, the control signal presents
state register, control signal can generate four states
to control the PE to complete the computation since
the control signal is 2-bit width, and the control logic
is the same as PE#F.
Algorithm 7 and Algorithm 8 are the pseudo code
of PE#L and PE#S. Fig.3 shows the improved archi-
tecture of PE#L and PE#S. The architecture of these
PEs is concise and can be easily implemented on
hardware compared to Huang’s work.
Algorithm 6: Pseudocode of processing element PE
of type E.
Input: x
i
,q
i
,Y
(i)
,M
(i)
,S
(i+1)
0
,Control,C
(i)
Output: C
(i+1)
,S
(i)
1 begin
2 S
temp
= 0 ;
3 if Control == St1 then
4 (CO
(i+1)
,SO
(i)
,S
(i)
w−2...1
) = (1,S
(i)
w−1...1
+ x
i
·
Y
(i)
+ q
i
· M
(i)
) + (C
(i)
&Control[0]);
5 (CE
(i+1)
,SE
(i)
,S
(i)
w−2...1
) = (0,S
(i)
w−1...1
+ x
i
·
Y
(i)
+ q
i
· M
(i)
) + (C
(i)
&Control[0]);
6 else if Control == St2 then
7 S
temp
= S
(i+1)
0
;
8 (CO
(i+1)
,SO
(i)
,S
(i)
w−2...1
) =
(CO
(i+1)
,SO
(i)
,S
(i)
w−2...1
) ;
9 (CE
(i+1)
,SE
(i)
) = (CE
(i+1)
,SE
(i)
) ;
10 else
11 (CO
(i+1)
,SO
(i)
,S
(i)
w−2...1
) =
(CO
(i+1)
,SO
(i)
,S
(i)
w−2...1
) ;
12 (CE
(i+1)
,SE
(i)
) = (CE
(i+1)
,SE
(i)
) ;
13 S
temp
= S
temp
14 S
(i)
=
(S
temp
)? (SO
(i)
,S
(i)
w−2...1
): (SE
(i)
,S
(i+1)
w−2...1
) ;
15 C
(i+1)
= (S
temp
)? CO
(i+1)
:CE
(i+1)
;
4 THE ARCHITECTURE OF RSA
COPROCESSOR
In order to meet the modern security demands
(Großchadl, 2000), the modulus should be at least
1024 bits long. The calculation of 1024-bit RSA in
software causes a very high computation cost since
the complexity of the modular exponentiation is n
3
for n-bit numbers. Especially in the application area
of embedded system, in one aspect, the computation
capability of the embedded CPU is very limited, so
special hardware accelerator of RSA computation is
A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC MONTGOMERY ARCHITECTURE
109






<[
L

0T
L




<[
L





6

L
T

 

&2

&(

6

62

6(


6


6

6

&

<

0

L
[
&
6
$




L
L
<[
L
L
0T

L
6
L
&



 +L
&2
 +L
&(
L
62
L
6(


+L
6
L
6
 +L
&


+ L
6
L
<
L
0

L
[
L
T
 L
&
0
0
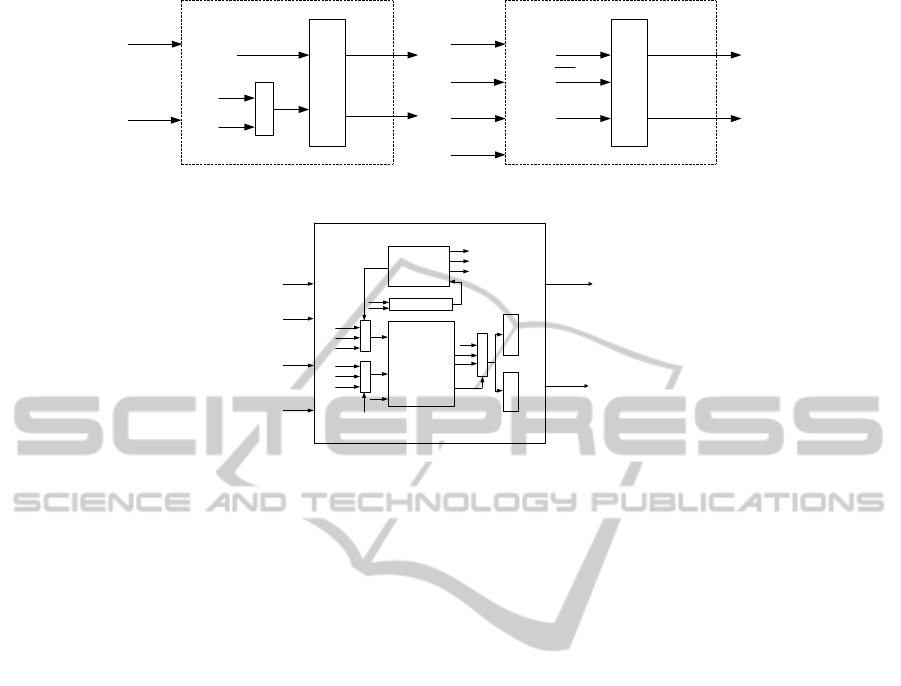
Figure 2: The architecture of F and E type PE.
Algorithm 7: Pseudocode of processing element
PEL of type L.
Input: Control
Output: S
(l)
1 begin
2 S
temp
= 0 ;
3 if Control == St1 then
4 (C
(l+1)
,S
(l)
w−1...1
) =
(S
(l)
w−1...1
) + (C
(l−1)
&Control[0]);
5 else if Control == St2 then
6 (C
(l+1)
,S
(l)
w−1...1
) =
(S
(l)
w−1...1
) + (C
(l−1)
&Control[0]);
7 else
8 (C
(l+1)
,S
(l)
w−1...1
) = (C
(l+1)
,S
(l)
w−1...1
)
Algorithm 8: Pseudocode of processing element
PE#i of type S.
Input: M
(i)
,S
i
,C
(i−1)
Output: S
(i)
sub
,CO
(i)
1 begin
2 (CO
(i)
,S
(i)
sub
) = (S
i
+ (∼ M
(i)
) +C
(i−1)
)
very necessary in this area; in another aspect, the
hardware resource is limited in embedded system,
hence the resource utilization of the RSA coproces-
sor should be as less as possible.
This section presents a description of the RSA
coprocessor architecture. Section 2 has already de-
scribed two algorithms of the modular exponentia-
tion. Comparing these two methods, the LR Binary
Method only needs a single hardware multiplier to
perform the squaring and multiplying, but the RL Bi-
nary method needs two hardware multipliers. Since
the Montgomery multiplier will consume huge hard-
ware resources. In order to design a tiny coprocessor,
our RSA coprocessor architecture uses the LR Binary
Method to complete modular exponentiation.
The Montgomery algorithm embeds into the LR
Binary Method forming Algorithm 9:
Algorithm 9: LR Binary Method with Montgomery
multiplier.
Input: M, e, N, Nr = 2
2n
mod N
Output: P := M
e
modN
1 begin
2 P := MonMul(1,Nr,N);
3 R := MonMul(M, Nr, N);
4 for i = h− 1 to 0 do
5 P := MonMul(P,P, N) ;
6 if e
i
= 1 then
7 P := MonMul(P,R, N) ;
8 P := MonMul(1,P, N);
9 return P;
The architecture of RSA coprocessor is showed
in Fig.4. As shown in Fig.4, the coprocessor mainly
consists of two blocks, which are Montgomery mul-
tiplier and Control Unit. The Montgomery multiplier
is the main computation engine which is used to com-
plete all modular multiplication, and the Control Unit
is used to complete the LR Binary Method. The input
Nr is the pre-computation of Montgomery multiplier.
In this design, we fully utilize the characteristic
of 4-input LUT to save FPGA resources. the output
of Montgomery multiplier is three signal, fist signal
S is the the Montgomery result that without subtract-
ing M, the S
sub
is the result of S− M, CS
e
is the carry
bit of S − M. The reason why our multiplier outputs
these signals is that these three signals plus the control
signal are just four signals, and these four signals can
use one level LUT. Otherwise, if the process of select-
ing S and S− M is executed inside the multiplier, out-
side the multiplier we must use extra one level LUT to
control the output of the multiplier. This point is very
important because the output signal of the multiplier
is very wide. For example, if we want to implement
2048-bit RSA, the width of output signal is 2048 bits.
if we use two level LUT, this will increase 2048 LUTs
to do the selecting. By above ways, our RSA module
is much smaller than previous work.
Compared with the previous works, firstly this
architecture doesn’t need any dedicated resources
SECRYPT 2011 - International Conference on Security and Cryptography
110





L
&
&RQWURO
 −H
6
−H
6
H
&
&RQWURO
L
&



&RQWURO
 −L
&6
L
VXE
6
L
0
L
0
L
VXE
6
+L
VXE
6
L
&6
 −L
&6
Figure 3: The architecture of F type PE and L type PE.

6
VXE
6
H
&6




1
Q


















1
Q







 !"
 
Figure 4: The architecture of RSA Coprocessor.
of FPGA. Consequently, it can be easily imple-
mented and mapped into FPGA produced by differ-
ent manufacturers. Secondly, our Montgomery mul-
tiplier architecture is easy to control and implement.
What’more, since the design fully utilize the charac-
teristic of FPGA resources, the resources consump-
tion is very compact.
5 FPGA IMPLEMENTATION AND
EVALUATION
In this section, we first compare some literature ar-
chitectures of Montgomery multiplier with our im-
proved architecture, and then we compare our RSA
coprocessor with some previous architectures. The
whole RSA coprocessor architecture has been imple-
mented in Verilog HDL and its result is verified by the
Java software implementation, what’s more this RSA
coprocessor module has been used in other embed
projects of ours as cryptographic computation unit
and it works well. This work has been verified very
well.
5.1 Comparison of Different
Architectures of Montgomery
Multiplier
In order to compare our work with the other works,
we have implemented three different sizes of Mont-
gomery multiplier, 1024, 2048 and 4096-bit respec-
tively. The comparison of resources utilization and
maximum frequencyare showed in Table 1. As shown
in Table 1, the area of our optimized architecture is
smaller than that of any other work. Compared with
the work (Huang et al., 2008), our architecture imple-
ments the whole Montgomery algorithm but the area
is nearly 80% of the work (Huang et al., 2008). Com-
pared with the work (McIvor et al., 2004a),(Shieh
et al., 2008), the Montgomery multiplier is smaller
than theirs because our PE and control architecture
are very simple.
5.2 Comparison of Different
Architectures of RSA Coprocessor
To compare the area/time utilization of our architec-
ture with previous works, we analyze the area utiliza-
tion and performance, the performance is denoted as
the number of cycles needed in modular exponentia-
tion. Table 3 lists some features of our work and some
previous works. Compared with the work (Shieh
et al., 2008), the new architecture is nearly half of the
area of Shieh (Shieh et al., 2008). What’s more, the
exponent E in modular exponentiation is only 32-bit
width in their architecture, our exponent E is 1024-
bit width. Their maximum frequency is higher than
ours. However, the critical path of our architecture
is the adder in the PE, this critical path can be eas-
ily changed by using more PEs, by doing this can in-
crease the maximum frequency. Compared with the
work (McIvor et al., 2004b), it needs less clock cy-
cles, because in the work (McIvor et al., 2004b) they
A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC MONTGOMERY ARCHITECTURE
111

Table 1: Comparison of hardware resource utilization and performance for 1024 -bit, 2048-bit and 4096-bit Montgomery
Modulo Multiplication.
Keysize Work Devices Freq(MHz) Min Latencyclks Area ( slices )
1024 McIvor (McIvor et al., 2004a) Xilinx V2-6000 123.6 1025 8294
1024 Huang (Huang et al., 2008) Xilinx V2-6000 100 1088 4178
1024 Our implementation Xilinx V2-6000 121 1056 3390
2048 McIvor (McIvor et al., 2004a) Xilinx V2-6000 110.6 2049 12490
2048 Huang (Huang et al., 2008) Xilinx V2-6000 100 2176 8337
2048 Our implementation Xilinx V2-6000 104 2080 6318
4096 McIvor (McIvor et al., 2004a) Xilinx V2-6000 92.81 4097 25474
4096 Huang (Huang et al., 2008) Xilinx V2-6000 100 4176 16648
4096 Our implementation Xilinx V2-6000 80 4128 12746
Table 2: Hardware resource utilization and performance of our RSA coprocessor, the platform is Xilinx V2-6000.
Keysize Freq(MHz) Area ( slices ) LUTs Flip-Flops
1024-bit 111 6470 11382 6763
2048-bit 97 12535 21761 13076
4096-bit 75 29045 46669 25373
Table 3: Hardware Resource Utilization and Performance of our RSA Coprocessor, the Platform is Xilinx V2-6000.
Work Freq(MHz) Area ( slices ) Average Latency (clks)
our work 111 6470 (1056)*1536
Shieh (Shieh et al., 2008) 152.49 12537 (1028)*1536
McIvor (McIvor et al., 2004b) 95.9 23208 (1025)*1024
used the RL Binary method. However, the area of
their design is nearly four times as large as ours.
6 CONCLUSIONS
In this paper, we optimize the Montgomery multiplier
architecture of Huang; what’s more we design a novel
architecture of RSA coprocessor which is based on
this new architecture. Compared with the previous
works, the new optimized Montgomery multiplier is
smaller than that of previous works, especially the
RSA coprocessor is smaller, at the same time it is not
so slower than previous works. Another feature of the
new architecture is that it doesn’t use any dedicated
resources on FPGA, compared with the work which
relied on the dedicated resources of specific FPGA,
the new architecture can be easily implemented on
FPGA with different architectures.
ACKNOWLEDGEMENTS
The work is supported by the National Science
and Technology Support Plan 2008BAH22B03,
2008BAH32B00, 2008BAH32B04; and the au-
tonomous research project of the State Key Labo-
ratory Of Information Security (SKLOIS), project
number:2010-16. National Natural Science Founda-
tion of China (Grant No.70890084/G021102), and
Knowledge Innovation Program of CAS (No.YYYJ-
1013).
REFERENCES
Cilardo, A., Mazzeo, A., Romano, L., and Saggese, G.
(2004). Carry-save Montgomery modular exponen-
tiation on reconfigurable hardware.
Großchadl, J. (2000). High-Speed RSA Hardware Based
on Barrets Modular Reduction Method. In Cryp-
tographic Hardware and Embedded SystemsCHES
2000, pages 95–136. Springer.
Harris, D., Krishnamurthy, R., Anders, M., Mathew, S.,
and Hsu, S. (2005). An improved unified scalable
radix-2 Montgomery multiplier. In Proceedings of the
17th IEEE Symposium on Computer Arithmetic, pages
172–178. Citeseer.
Huang, M., Gaj, K., Kwon, S., and El-Ghazawi, T. (2008).
An Optimized Hardware Architecture for the Mont-
gomery Multiplication Algorithm. Lecture Notes in
Computer Science, 4939:214.
Kaya-Koc, C. (1995). RSA Hardware Implementation. RSA
Data Security, Inc., Version, 1.
McIvor, C. et al. (2004a). FPGA Montgomery multiplier
architectures-a comparison.
SECRYPT 2011 - International Conference on Security and Cryptography
112

McIvor, C., McLoone, M., and McCanny, J. (2004b). Modi-
fied Montgomery modular multiplication and RSA ex-
ponentiation techniques. IEE Proceedings-Computers
and Digital Techniques, 151(6):402–408.
Mclvor, C., McLoone, M., and McCanny, J. (2003). Fast
Montgomery modular multiplication and RSA crypto-
graphic processor architectures. In Conference Record
of the Thirty-Seventh Asilomar Conference on Signals,
Systems and Computers, 2003, pages 379–384.
Montgomery, P. (1985). Modular multiplication with-
out trial division. Mathematics of computation,
44(170):519–521.
Shieh, M.-D., Chen, J.-H., Wu, H.-H., and Lin, W.-C.
(2008). A new modular exponentiation architecture
for efficient design of rsa cryptosystem. Very Large
Scale Integration (VLSI) Systems, IEEE Transactions
on, 16(9):1151 –1161.
Tenca, A. and Koc¸, C¸ . (1999). A scalable architecture for
Montgomery multiplication. Lecture Notes in Com-
puter Science, pages 94–108.
A TINY RSA COPROCESSOR BASED ON OPTIMIZED SYSTOLIC MONTGOMERY ARCHITECTURE
113