
A COMPARATIVE STUDY OF THE TEMPERATURE
DEPENDENCE OF LASING WAVELENGTH OF
CONVENTIONAL EDGE EMITTING STRIPE LASER AND
VERTICAL CAVITY SURFACE EMITTING LASER
Niazul Islam Khan
1
, Samiul Hayder Choudhury
2
and Arif Ahmed Roni
1
1
Faculty of Engineering and Computer Science, Ulm University, Ulm, Germany
2
Department of Electronic System, Aalborg University, Aalborg, Denmark
Keywords: Gain guided laser, Lasing wavelength, Stripe laser, Spectral alignment, VCSEL.
Abstract: Semiconductor lasers are the integral parts of optical communication systems. The temperature dependence
of the lasing wavelength of a laser is an important issue because it is used in different environment with
varying thermal conditions. In this paper, a comparative study of the temperature dependence of lasing
wavelength of two types of laser diode has been presented. The comparison was made between an
InGaAsP/InP stripe geometry edge-emitting laser and vertical cavity surface emitting laser (VCSEL) with
GaAs in the active region. For both cases, the temperature dependence was observed for different heat sink
temperatures ranging from 20ºC to 50ºC at an interval of 5ºC for an operating current of 0.763A and
1.88mA respectively. The lasing wavelength shifts for stripe laser and VCSEL have been found to be
0.3nm/K and 0.06nm/K respectively. VCSEL exhibits significantly greater thermal stability than stripe
laser. The result has also been elucidated with a comprehensive theoretical excerpt.
1 INTRODUCTION
Modern optical communication systems for military
or aerospace applications work in a wide range of
temperature, typically from -30ºC to +50ºC
(Jamieson, 1981). Therefore, the study of
temperature dependence on laser operation is of
prime importance as it is the most important part of
the transmission end of optical communication
system. Laser characteristics like lasing wavelength,
threshold current density, conversion efficiency etc.
are considerably affected by temperature. In this
paper, we have studied the temperature dependence
of the lasing wavelength of two types of laser,
namely, the edge emitting stripe geometry gain
guided laser and the Vertical Cavity Surface
Emitting Laser (VCSEL). Figure 1 depicts the
schematic diagram of a double-heterostructure
InGaAsP stripe geometry edge emitting laser with
gain guided structure that is considered in our study.
A simple sketch of a VCSEL is shown in Figure
2.
Figure 1: Schematic diagram of double-heterostructure
InGaAsP stripe laser with gain guided structure.
For edge emitting stripe laser, the lasing
wavelength is primarily determined by the peak-gain
wavelength whereas for VCSEL lasing wavelength
is fixed by the cavity wavelength (Kondow et al.,
2000). However, this temperature dependence is
predominantly influenced by two of the material
properties: refractive index and the bandgap energy.
Temperature dependence of refractive index and
bandgap wavelength has been studied for GaAs and
other materials in (Camassel et al., 1975- Tanguy,
1996).
141
Islam Khan N., Hayder Choudhury S. and Ahmed Roni A..
A COMPARATIVE STUDY OF THE TEMPERATURE DEPENDENCE OF LASING WAVELENGTH OF CONVENTIONAL EDGE EMITTING STRIPE
LASER AND VERTICAL CAVITY SURFACE EMITTING LASER.
DOI: 10.5220/0003512101410145
In Proceedings of the International Conference on Data Communication Networking and Optical Communication System (OPTICS-2011), pages
141-145
ISBN: 978-989-8425-69-0
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: Schematic diagram of VCSEL (active layer
contains GaAs and DBR mirrors contain Al
0.7
Ga
0.3
As
/GaAs quarter-wave Bragg stacks) (Jamieson, 1981) other
materials in (Camassel et al., 1975- Tanguy, 1996).
The paper is organized as follows: in the
subsequent section the temperature dependence of
the lasing wavelength of laser has been explained
elaborately and then the outcomes of our study has
been presented with numerical findings.
2 EFFECT OF TEMPERATURE
ON LASING WAVELENGTH
The lasing wavelength of a laser depends on several
factors like chemical composition and doping of
active region and external physical parameters, such
as temperature, pressure, magnetic field etc. (Eliseev
et al., 1994). In this paper, we have confined our
study only to the temperature dependence of lasing
wavelength. However, this temperature dependence
of lasing wavelength varies for different types of
laser diodes.
The well-known resonance condition for the
cavity resonant wavelength, λ is given by (Keiser,
1991),
m
nL2
(1)
where, ‘n’ is the spatially averaged refractive index,
‘
L’ is the resonator length and ‘m’ is a positive
integer.
In longitudinal multimode lasers like stripe laser,
ridge-waveguide laser and buried heterostructure
laser, the resonator is relatively long (typically,
hundreds of times of λ which is in between few
hundred micrometers and a few millimeters) and due
to this long resonator length, lots of longitudinal
modes satisfying the resonance condition overlap the
active material gain bandwidth (Choquette and Hou,
1997, RP Photonics). Longitudinal mode spacing
between two neighboring modes,
is given by
(Keiser, 1991),
gr
Ln2
2
(2)
where,
n
gr
is the group refractive index. From Eq. 2,
we observe that long resonator results in very
smaller mode spacing between two consecutive
resonant modes and hence very higher spectral
density of the longitudinal modes. Now,
differentiating Eq. 1 with respect to temperature,
T
and neglecting the thermal expansion of the
resonator length, we obtain,
dT
dn
ndT
d
.
(3)
The temperature dependence of refractive index of
the laser active medium
dT
dn
can be approximated
by (Numai, 2004),
4
10)5~2(
d
T
dn
(4)
which implies that the refractive index has a positive
gradient with respect to temperature. Consequently,
we have from Eq. 3,
0
d
T
d
(5)
Eq. 5 indicates that with the increase of temperature,
the resonant modes shift to the right along the
wavelength axis. Additionally, if we take the thermal
expansion of the laser cavity into account, it also
leads to the shift of resonant modes to longer
wavelengths (Unger, 2000). On the other hand,
temperature dependence of bandgap wavelength,
g
g
W
hc
( Precker, 2007) is given by,
gg
g
W
hc
dW
d
dT
d
(6)
where, h is the Planck’s constant, c is the velocity of
light and
g
W
is the bandgap-energy. Now, Eq. 6 can
be written as,
dT
dW
W
hc
dT
d
g
g
g
.
2
(7)
The increase in temperature yields in the shrinkage
of the semiconductor material band gap which is
given by Varshni’s empirical equation (Varshni,
1967),
OPTICS 2011 - International Conference on Optical Communication Systems
142

Figure 3: Schematic diagram of temperature dependence
of material gain profile and resonant modes (g
th
indicates
threshold gain).
T
T
WTW
gg
2
)0()(
(8)
where,
,),0(
g
W
are the fitting parameters. It is
obvious from Eq. 8 that
0
d
T
dW
g
. This is equivalent to
so called ‘red-shift,’ i.e.
0
dT
d
g
and this causes
entire gain profile to shift to the right also. But the
laser gain shift to larger wavelength
dT
d
g
is faster
(about a factor of 4 to 5) than the shift of the cavity
resonant modes
dT
d
(Choquette and Hou, 1997).
So, for multimode lasers the temperature behavior of
the lasing wavelength is mostly influenced by the
temperature dependent drift of the gain spectrum of
the active region (Blokhin et al., 2006). Due to this
relative shift of modes and gain profile, larger
wavelength modes move closer to peak-gain
wavelength, as temperature increases. This
temperature dependence of lasing wavelength for a
multimode laser is illustrated in Figure 3. The figure
shows the schematic diagram of temperature
dependence of the material gain profile and the
densely spaced resonant modes (vertical lines) of
long Febry-Perot resonator. The solid gain profile is
for temperature
T
1
and the dashed gain profile is for
temperature
T
2
, where T
2
>T
1
. As temperature
increases from
T
1
to T
2
, higher wavelength (lower
order) modes get closer to the peak-gain wavelength.
But for VCSEL, the resonator length is very
small (only a few microns typically 1-3 µm). So
from Eq. 2, the mode spacing between two
consecutive resonant modes is large compared with
that of long resonator multimode lasers. The mode
spacing of VCSEL is approximately several orders
of magnitude larger than that of a stripe laser.
Figure 4: Schematic diagram of temperature dependence
of material gain profile and resonant modes for a very
short resonator.
Because of the fact that, the resonant modes are
far away from each other, one single cavity resonant
mode spectrally overlaps the gain medium
bandwidth (Choquette and Hou,1997) allowing the
VCSEL to be single mode laser. The spectral
alignment between the resonant single optical mode
and the gain profile mainly influence the
temperature dependence of VCSEL lasing
wavelength. Figure 4 shows the temperature
dependence of lasing wavelength of VCSEL. As
temperature increases from
T
1
to T
2
, both the gain
profile and the resonant mode shift to a new position
of longer wavelength as in the case for stripe laser.
But still there is one mode in optical cavity because
the other non overlapping resonant modes locate far
away from the gain bandwidth and the new position
of the resonant mode is now the lasing wavelength.
Therefore, except for a detuned laser (where the
overlap between the single resonant mode and the
gain bandwidth is very weak), the wavelength shift
of the lasing wavelength for VCSEL is determined
mainly by the wavelength shift of the resonant single
mode but not by the material gain profile as in the
conventional edge emitting laser (Michalzik and
Ebeling).
3 RESULTS AND DISCUSSION
This section presents the observed results of our
study. As mentioned before, we have studied the
temperature dependence of the lasing wavelength of
stripe laser and VCSEL for an operating current of
0.763 A and 1.88 mA respectively. The outcomes of
our study are visualized in Figure 5 and Figure 6.
The figures show the observed lasing wavelength
shift for different heat sink temperature for the stripe
laser and VCSEL respectively. From Figure 5, we
can calculate the lasing wavelength shift for the
stripe laser by calculating the slope as,
A COMPARATIVE STUDY OF THE TEMPERATURE DEPENDENCE OF LASING WAVELENGTH OF
CONVENTIONAL EDGE EMITTING STRIPE LASER AND VERTICAL CAVITY SURFACE EMITTING LASER
143
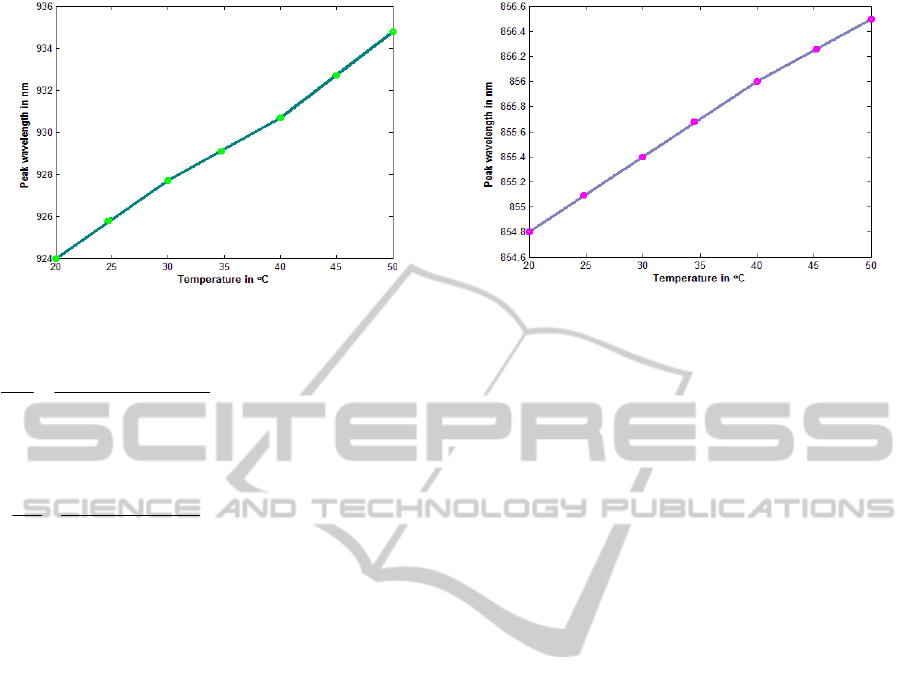
Figure 5: Temperature dependence of peak wavelength for
the stripe laser at an operating current of 0.763 A.
KnmCnm
C
C
nmnm
dT
d
p
00
00
/3.0/3.0
3040
7.9277.930
Similarly, the lasing wavelength shift for VCSEL is
given by,
KnmCnm
C
C
nmnm
d
T
d
p
00
00
/06.0/06.0
3040
4.8550.856
Therefore, the lasing wavelength shift of stripe laser
is significantly greater than that of the VCSEL. The
smaller wavelength shift of VCSEL can be attributed
to the fact that for VCSEL, the temperature
dependence of lasing wavelength is primarily
determined by the temperature dependence of
refractive index of the laser active medium, whereas
for stripe geometry edge-emitting multimode laser,
the temperature dependence of lasing wavelength is
dominated by the temperature dependent drift of the
gain profile, which is the result of temperature
dependence of bandgap wavelength.
4 CONCLUSIONS
As VCSEL is selective to one wavelength, the lasing
wavelength is mainly influenced by the temperature
dependence of only refractive index, but for
longitudinal multimode lasers like stripe lasers, the
lasing wavelength is dependent mostly on
temperature dependence of gain profile. So, lasing
wavelength is more prone to change for stripe lasers
than for VCSEL. In this paper, we obtained the
temperature dependent wavelength shift as 0.3
nm
/ºK for InGaAsP/InP stripe laser and and 0.06 nm/ºK
for GaAs based VCSEL respectively. This
temperature stable behavior of VCSEL spectrum has
gone a long way to add another plus point to its
other versatile advantages.
Figure 6: Temperature dependence of peak wavelength for
VCSEL at an operating current of 1.88 mA.
REFERENCES
Blokhin S. A. et al., 2006. Experimental Study of
Temperature dependence of Threshold Characteristics
in Semiconductor VCSELs Based on Submonolayer
InGaAs QDs. Physics of Semiconductor Devices, vol.
40, no. 10, pp. 1232–1236.
Camassel J., Auvergne D. and Mathieu H., 1975.
Temperature dependence of the band gap and
comparison with the threshold frequency of pure GaAs
lasers. Journal of Applied Physics, vol. 46, no. 6.
Choquette K. D. and Hou H. Q., 1997. Vertical-Cavity
Surface Emitting Lasers: Moving from Research to
Manufacturing. Proceedings of IEEE, vol. 85, no. 11,
pp.1730-1739.
Eliseev P. G., Drakin A. E. and Pittroff W., 1994. A Study
of Laser Emission Wavelength Variations in 1.5 µm
InGaAsP/InP BRS Laser Diodes: Theoretical Model
and Experiment. IEEE Journal of Quantum
Electronics, vol. 30, no. 10.
Gaikwad S. A., Samuel E. P., Patil D. S. and Gautam D.
K., 1975. Temperature dependent analysis of
refractive index, bandgap and recombination
coefficient in nitride semiconductor lasers. Journal of
Applied Physics, vol. 46, no.6.
Jamieson T. H., 1981. Thermal effects in optical systems.
Optical Engineering, vol. 20, no. 2.
Keiser G., 1991. Optical Fiber Communications. Mcgraw
Hill, 2
nd
Edition.
Kondow M., Kitatani T., Nakahara K. and Tanaka T.,
2000. Temperature Dependence of Lasing Wavelength
in a GaInNAs Laser Diode. IEEE Photonics
Technology Letters, vol. 12, no. 7.
Michalzik R. and Ebeling K. J., Operating principle of
VCSELs.
Numai T., 2004. Fundamentals of Semiconductor Lasers.
Springer-Verlag New York.
Precker J. W., 2007. Simple Experimental Verification of
the Relation Between the Bandgap Energy and the
Energy of Photons Emitted by LEDs. European
Journal of Physics, vol. 28, pp. 493-500.
OPTICS 2011 - International Conference on Optical Communication Systems
144

RP Photonics. http://www.rp-photonics.com/
Unger P., 2000. Introduction to power laser diodes.
Topics of Applied Physics, vol. 78, pp. 1–54.
Tanguy C., 1996. Temperature dependence of the
refractive index of direct band gap semiconductors
near the absorption threshold: Application to GaAs.
Journal of Applied Physics, vol. 80, no. 8.
Varshni Y. P., 1967. Temperature Dependence of the
Energy Gap in Semiconductors. Physica 34, pp. 149-
154.
A COMPARATIVE STUDY OF THE TEMPERATURE DEPENDENCE OF LASING WAVELENGTH OF
CONVENTIONAL EDGE EMITTING STRIPE LASER AND VERTICAL CAVITY SURFACE EMITTING LASER
145
