
PRIVACY-PRESERVING SMART METERING WITHOUT A
TRUSTED-THIRD-PARTY
Tobias Jeske
Institute for Security in Distributed Applications, Technical University of Hamburg, 21079 Hamburg, Germany
Keywords:
Smart metering, Smart grid, Cryptography, Zero-knowledge protocols, Privacy.
Abstract:
Smart meters report the current electricity consumption over the internet back to their energy providers. Finely-
sampled power consumption enables the energy provider to learn the habits of the customer’s household in
which the smart meter is installed. This paper presents a protocol which preserves customer privacy but
also allows the detection of unregistered smart meters and prevents spamming and replay attacks. A trusted-
third-party is not needed. This protocol, whose security proof relies on the strong RSA assumption and the
random oracle model, is based on zero-knowledge techniques. The protocol has been implemented on different
hardware platforms and benchmark results are given.
1 INTRODUCTION
For energy providers it is important to know the
pattern of their customers’ daily electricity consump-
tion. A difference between supply and demand can
impinge on power frequency and voltage (M¨uller,
2010). Today energy providers plan electricity
demands on the basis of statistical data based on
the knowledge of past power consumption and on
the experience of how power consumption will vary
in the future (e.g. seasonal variations, upcoming
mega-events).
Electricity demands fluctuate over a day and are
generally at their highest in the morning and evening.
An energy provider uses different sources to supply
electricity. Base load power stations (nuclear power
plants, lignite-fired power plants) are characterized
by a nearly constant energy transfer running the
whole day, offering electricity at a low price. The
investment in new nuclear power plants is high,
whereas the costs of operation are comparatively
low. For this reason, it is economically advantageous
to continuously operate them at maximum power.
Lignite-fired power plants usually have long start-up
times, which also make them unsuitable to compen-
sate peaks in the power demand. Instead, peak-load
electricity generation plants like pumped-storage/gas
turbine power stations are used. They have short
start-up times, are more flexible and provide energy
whenever needed but at higher costs. If the demand
is too high or the energy provider does not have any
power plants, electricity is bought at the electricity
stock exchange.
Different electricity sources marked by varying
prices and fluctuating demands necessitate a sophis-
ticated resource planning. Renewable energies like
wind and solar power make the situation even more
difficult. Energy generation depends on the weather;
in some countries like Germany energy providers are
obliged to feed renewable energy into the electricity
grid (German Federal Ministry of Justice, 2008).
Energy providers have a huge interest in pre-
cisely predicting their customers’ electric energy
consumption in order to be always able to choose
the economically most advantageous energy source.
Knowing the current electricity demands gives more
planning stability and permits differentiated price
models. Energy providers couple the costs for electric
energy generation to the demands, for example by
charging higher fees during peak hours, and give
customers incentives to save energy and money
(M¨uller, 2010) (McDaniel and McLaughlin, 2009).
1.1 Smart Meter & the Smart Grid
Smart meters can report current electricity consump-
tion back to their energy providers (e.g. every 15
minutes) (M¨uller, K. J. et al., 2011). Berg Insight
estimates that 302.5 million smart meters will be
114
Jeske T..
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY.
DOI: 10.5220/0003513001140123
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 114-123
ISBN: 978-989-8425-71-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

installed worldwide in 2015 (Berg Insight, 2010).
In Germany, the Energiewirtschaftsgesetz has made
smart meters compulsory in new and renovated
private houses (German Federal Ministry of Justice,
2005).
Modern smart meters visualize the power con-
sumption in real-time and present it to the customers.
The customer is notified when the price per kW/h
is attractive, which enables shifting usage hours
of electrical equipment (e.g. air conditioning) to
non-peak hours.
The Smart Grid integrates all actors in the elec-
tricity market into a complete system, in which the
producer, storage and consumer of electrical energy
communicate with each other. Smart meters are im-
portant devices in the Smart Grid concept (McDaniel
and McLaughlin, 2009). They allow to control and
communicate with electrical devices in the household
(the smart meter could start the washing machine
in a specific time interval when the kW/h price is
low) and to predict power consumption. A running
washing machine, for example, could inform the
smart meter of its power consumption for the wash
cycle. In this case the smart meter would forward this
information to the energy provider to optimize the
resource planning.
1.2 Smart Meter & the Privacy Problem
Sending finely-sampled power consumption data to
the energy provider allows the energy provider to
learn the habits of the consumer’s household in which
the smart meter is installed. The electrical equipment
of a household has a characteristic energy profile
easy to identify (M¨uller, 2010).
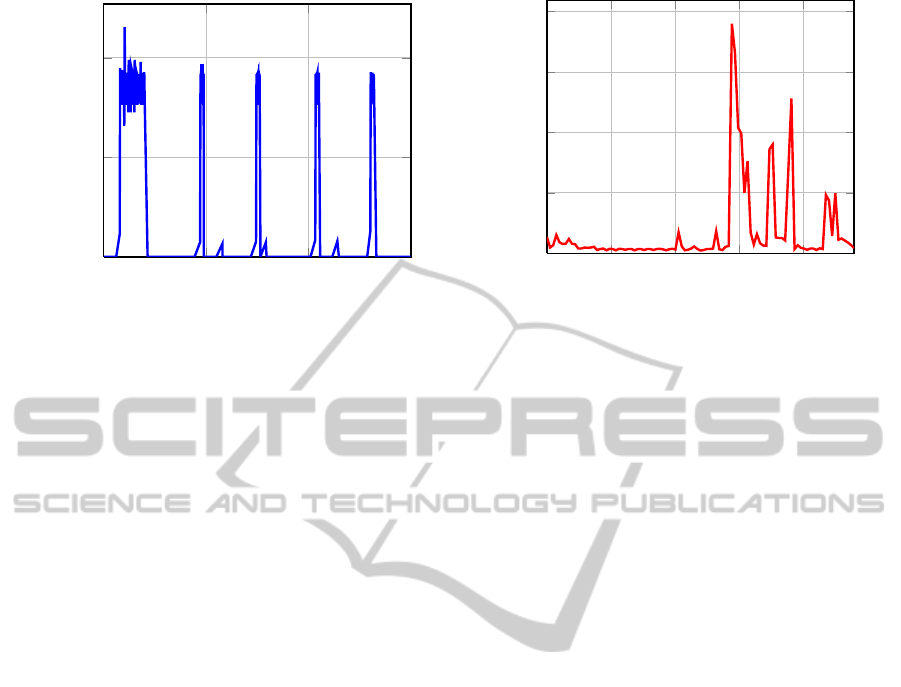
Figure 1 (left) represents the energy profile of
a baking oven marked by a noticeable high energy
consumption of about 1800 W. At the beginning,
during the heating-up period, the oven is heated from
room temperature to the target temperature. Then the
heating element is switched on from time to time to
keep up the temperature. This power consumption
pattern is typical and characteristic of most electric
baking ovens.
If one superimposes the consumption of all
electrical equipment, one can still recognize a
baking oven because of its high individual energy
consumption. Even if a customer employs more
devices consuming much electric energy (e.g. an air
conditioner), different devices can be identified due to
usage time and curve progression. A fridge is usually
the only high power consumption device running
over night. Figure 1 (right) shows the electrical
energy consumption of an entire day. Despite the
fact that the resolution is only four samples per hour,
electrical equipment, for instance a baking oven and
a dishwasher, can be detected in the chart.
What is more difficult but not impossible is the
identification of electrical equipment with low power
consumption. Even in this case, usage time and
the fact that most of the electrical equipment is
not continuously switched on makes it possible to
identify individual devices. Filtering out already
identified devices improves the identification of the
remaining ones.
M¨uller (M¨uller, 2010) gives the following criteria to
identify electronic equipment:
1. Power consumption
2. Load profile of different device types
3. Typical operating cycle
4. Time of usage
5. Frequency of usage
If someone evaluates the energy profiles, it is for
instance easy to see when someone is at home (light,
TV etc. is switched on). This information is quite
useful for burglars. Questions regarding living habits
like ”How many times do the household members
cook?” or ”When does the customer go to the toilet
at night?” (light is switched on!) are not private any
longer.
In summary, on the one hand, the energy provider
benefits from knowledge of a detailed energy profile
to improve the energy consumption forecast. On the
other hand, customers do not want energy providers
to gain insight into their habits. In this paper we
present a new solution to solve these two (conflicting)
requirements.
The paper is structured as follows: In section 2
we present our scenario and aims for privacy-
preserving smart metering. In section 3 we explain
the main concept as well as some general ideas be-
hind our solution. In section 4 we present a technical
description. Implementation results are presented in
section 5. In section 6 we cover related work before
drawing a conclusion in section 7.
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY
115
18:50 18:52 18:54
0
1,000
2,000
time [h:min]
power [W]
5:00 10:00 15:00 20:00
0
500
1,000
1,500
2,000
time [h:min]
power [W]
Figure 1: Electrical power consumption of a baking oven (left) and a single household over 24h (right).
2 SCENARIO & AIMS FOR
PRIVACY-PRESERVING
SMART METERING
In our scenario, every household has one smart
meter communicating with one energy provider. If
a household has several metering devices, a MUC
(Multi Utility Communication) controller is usually
used as a gateway. In our protocol the MUC device
acts as the smart meter for simplification. The meters
and MUC of a household build a trusted environment
between each other.
Every smart meter communicates with the en-
ergy provider over a standard network protocol like
TCP/IP. We require that energy providers cannot
identify smart meters by the sender address (e.g. IP
or MAC address). In section 5 we discuss how this
requirement can be fulfilled in real-world implemen-
tations.
Other solutions usually require a trusted-third-party
(TTP) to manage membership (Petrlic, 2011) (Garcia
and Jacobs, 2010). We take the view that a TTP is
difficult to realise in practice. First, energy providers
want to have the flexibility to add and remove smart
meters from their network without contacting a TTP.
Secondly, we believe that customers who do not trust
the energy provider have no motivation to trust a TTP
(e.g. run by the government) instead.
We require that smart meters can periodically
(e.g. every 15 minutes) send their power consumption
to the energy provider for load reporting. The
customer’s privacy must be preserved.
The smart meter accumulates the energy consump-
tion and submits it to the energy provider for billing
purposes (e.g. every month). We assume that the
smart meter regularly downloads a billing policy
from the energy provider in an authenticated way and
charges the energy consumption against the policy.
During the billing process, the customer must be
identified.
Smart meter authentication is important in every
protocol stage. Energy providers must be able to
verify if the consumption data was sent from a valid
smart meter that is part of the provider’s grid.
In summary, here is a list of the aims we want
to achieve with our solution:
1. Anonymity
The privacy of every customer is preserved. It
is impossible for the energy provider or anybody
else to get information about the customer’s living
habits.
2. Unlinkability
Data packets that are sent from the same smart
meter at different times for the purpose of load
reporting cannot be linked to each other.
3. Misauthentication Resistance
Energy providers can detect unregistered smart
meters and only accept data sent from smart me-
ters being part of the provider’s network.
4. Invoicing
Smart meters send the energy provider cost cal-
culations containing the power consumption for
a certain time interval. The energy provider can
identify smart meters for invoicing.
5. Revocability
It is possible to remove smart meters from the
provider’s network. If an energy provider with-
draws from the contract concluded with the cus-
SECRYPT 2011 - International Conference on Security and Cryptography
116

tomer, data packets coming from the smart meter
must be rejected.
6. Prevention of Spamming and Replay Attacks
Malicious customers are not able to spam the en-
ergy provider with faked data and consequently
spoil the power consumption forecast. Replay at-
tacks are prevented. Each data packet which con-
tains measurement data from a unique smart me-
ter and which covers a unique time interval can be
submitted only once to the energy provider. This
prevents replay attacks.
7. No Delay
It is important for load reporting that smart meters
submit consumption data to the energy provider
without any delay. We require a maximum delay
of 15 minutes.
8. Data Quality / Correctness
The energy provider must be assured that the
smart meter correctly sends the consumption data.
9. No TTP / Practicability
A protocol should not require a TTP for key or
membership management. The energy provider
can add (or remove) smart meters from the grid
without the help of another party.
3 MAIN CONCEPT
In this section we explain the main concept behind
our solution to achieve all aims listed in section 2. A
detailed and more technical explanation follows in
the next section.
Our protocol consists of two sub-protocols, the
invoicing and the load reporting protocol.
A smart meter (S ) uses the invoicing protocol to
send the accumulated electric power consumption to
the energy provider (P ). Basically, S uses standard,
asymmetric key cryptography to sign and encrypt the
invoicing data. The identity of the customer and the
corresponding smart meter is revealed (aim 4).
In general, the load reporting protocol is based on
the idea of group signature schemes. S is a member
of a group of smart meters with P as the group
manager. Using group signature schemes, S signs
the consumption data for load reporting in the name
of the group. P can only verify group membership.
Group signature schemes allow us to separate valid
smart meters belonging to the energy provider’s
grid from other (malicious) smart meters (aim 3).
S stays anonymous. Even if S signs two (different)
messages, it is practically impossible for P to find
out that both signatures come from the same smart
meter. Using a group signature scheme, we achieve
the first two aims, anonymity and unlinkability.
During the invoicing protocol, S is added to the
group because S is identified. S creates a ticket
and P signs it without knowing it. Later, S uses
signature and ticket to prove group membership
during submission of anonymous load reporting
data. We use zero-knowledge protocols in order
not to reveal signature and ticket and to preserve
S ’s privacy. Every ticket can be used only once to
prevent replay attacks (aim 6). The signature for the
secret ticket contains a time stamp, which allows us
to diminish the threat of spamming attacks (aim 6).
4 PROTOCOL DETAILS
As explained in the previous section, we need a group
signature scheme for our protocol. Our solution
is based on the Camenisch and Lysyanskaya (CL)
signature scheme because of its efficiency (Ca-
menisch and Lysyanskaya, 2003). Its security relies
on the strong RSA assumption. We use the version
of Camenisch and Groth to improve performance
(Camenisch and Groth, 2005).
The CL signature scheme consists of two pro-
tocols. Using the first protocol, a signer issues
a signature on a committed value. In the second
protocol, the party knowing the committed value can
prove knowledge of a signature by using a signature
proof of knowledge.
This paper follows the notation of Camenisch
and Stadler (Camenisch and Stadler, 1997) to
describe zero-knowledge proofs of knowledge.
4.1 Setup
Every smart meter S has a long-term secret key
S
LTSK
and long-term public key S
LTPK
. S
LTSK
serves
as S ’s signing key and S
LTPK
is the corresponding
verification key. The energy provider P also has
a long-term key pair P
LTSK
and P
LTPK
, which is
used for sending encrypted data to P . The key pairs
are created once by the corresponding parties. We
assume that S
LTPK
unambiguously identifies S .
In our protocol n = p · q represents a RSA mod-
ulus of bit length l
n
, where p and q are two large
safe prime numbers only known to P . P randomly
chooses a,b,d, f
1
, f
2
,g,h ∈
R
QR
n
, where QR
n
de-
notes the set of quadratic residues modulo n. It also
sets TS
log
∈ Z
n
, a time delay in which S cannot
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY
117

submit data to P .
When the customer concludes a contract with a
new energy provider P , S establishes a secure and
authenticated connection with P . This could e.g. be
realised using SSL/TLS where S has pre-installed
root certificates to verify P ’s certificate or alterna-
tively public key.
S submits the meter number together with S ’s public
key to P for registration. To identify the customer
S could also send P a PIN code over the secure
channel. The customer could e.g. receive the PIN
from P via a letter.
4.2 Invoicing
S runs the invoicing protocol to send P the cost
calculation comprising the power consumption for a
certain interval. At the end of the protocol, S has not
only sent P the accumulated power consumption, but
the smart meter is also in possession of a signature
for a secret ticket x which allows S to anonymously
send P load reporting data (figure 2). The invoicing
protocol corresponds to the first protocol of the CL
signature scheme.
The protocol works as follows. First, S ran-
domly chooses a secret number x, the ticket. The
ticket is embedded in a Groth commitment C
x
1
(see appendix 7) and the power consumption is
accumulated in data
invoicing
. S creates a signature
S
1
with its long-term private key S
LTSK
for values
C
x
1
and data
invoicing
. Afterwards S sends C
x
1
, S
1
,
data
invoicing
and its public key (as an identifier) to
P . The consumption data data
invoicing
and S
LTPK
are encrypted under P ’s public key. If S is a valid
smart meter and part of P ’s grid, P accepts the
consumption data and otherwise rejects them (aim
3, aim 5). If S is a valid smart meter, P creates a
signature for S ’s secret ticket x.
The signature creation and expiration time TS
p
and TS
e
are embedded in the signature. After P has
sent the signature parameters (r
′
,e,v,TS
P
,TS
e
) back
to S , S verifies the signature (s,e,v, TS
P
,TS
e
) and
checks the time stamps. It is important that TS
e
is
coarse enough (e.g. years or months) so that P cannot
identify S by choosing a unique time stamp for S .
4.3 Submitting Consumption Data for
Load Reporting
Using the load reporting protocol, S can anony-
mously send P the energy consumption of a certain
interval. The protocol is shown in figure 3. The
second protocol of the CL signature scheme is used
as a basic building block.
First, S proves in zero-knowledge that it is in
possession of a valid ticket x, i.e. that S has a valid
signature (s,e,v,T S
P
,TS
e
) from P for ticket x.
Second, S proves in zero-knowledge that TS,
the time stamp of the measured power consumption
data
reporting
, is greater than TS
P
+ TS
log
. If this is
not the case, S submits data too soon and P rejects
the submission. An anonymous submission is only
allowed every TS
log
minutes.
The considerations mentioned above lead with
C
v
= vb
˜r
, ˜r ∈
R
(0,2
l
n
/2
) to the following signature
proof of knowledge (SPK):
SPK
(ε,σ,γ) :
d = C
2
l
E
+ε
v
a
−x
b
σ
f
1
−4γ
f
2
−TS
e
∧
TS > TS
p
+ TS
log
(m) (1)
Every ticket x can be used only once to prevent replay
attacks. S reveals x and TS
e
in clear text to P , who
puts them on a blacklist BL. To limit the blacklist
size, P removes expired tickets from the blacklist
from time to time.
The message m in proof (1) contains the mea-
surement data data
reporting
and a commitment
C
′
x
= a
x
′
b
′
r
1
for x
′
, the ticket for the next submission
step. If S has followed the protocol and is a valid
smart meter, P creates a signature for x
′
like in the
invoicing protocol. S can use ticket x
′
to submit
consumption data anonymously after TS
′
P
+ TS
log
minutes.
4.4 Security Analysis
In our security analysis we consider three players, a
trusted S , P and an untrusted S . We here want to
discuss how our solution resists common attacks in a
smart metering environment.
The security of the underlying CL signature scheme
and our zero-knowledge proofs is based on the RSA
assumption and the random oracle model. We re-
fer the reader to (Camenisch and Groth, 2005) and
(Groth, 2005) for more information.
4.4.1 Trusted Smart Meter
Customers manipulate their smart meter to forge the
power consumption data for invoicing (electricity
theft) and load reporting:
SECRYPT 2011 - International Conference on Security and Cryptography
118

S P
commitment for x:
x ∈
R
(0,2
l
x
)
r
1
∈
R
(0,2
l
n
)
C
x
1
= a
x
b
r
1
mod n
S
1
= S
S
LTSK
(C
x
1
|data
invoicing
)
validating:
Is S a valid smart meter?
signing x:
r
′
∈
R
(0,2
l
n
)
e ∈
R
(0,2
l
e
) ∧ e is prime
E = 2
l
E
+ e
v = (C
x
1
b
r
′
d f
1
4TS
P
f
2
TS
e
)
1/E
mod n
signature for x:
s = r
1
+ r
′
signature = (s,e,v,TS
P
,TS
e
)
-
E
P
LTPK
[S
LTPK
,data
invoicing
]
C
x
1
,S
1
(r
′
,e,v,TS
P
,TS
e
)
Figure 2: S submits to P the accumulated power consumption for invoicing.
S P
commitment for x
′
:
x
′
∈
R
(0,2
l
x
)
r
′
1
∈
R
(0,2
l
n
)
C
′
x
1
= a
x
′
b
r
′
1
mod n
validating:
Is S a valid smart meter?
(x,TS
e
)
?
∈ BL
signing x
′
:
r
′′
∈
R
(0,2
l
n
)
e
′
∈
R
(0,2
l
e
) ∧ e
′
is prime
E
′
= 2
l
E
+ e
′
v
′
= (C
′
x
1
b
r
′′
d f
1
4TS
′
P
f
2
TS
′
e
)
1/E
′
mod n
signature for x:
s
′
= r
′
1
+ r
′′
signature = (s
′
,e
′
,v
′
,TS
′
P
,TS
′
e
)
-
SPK[..]
data
reporting
, C
′
x
1
E
P
LTPK
[data
reporting
,TS, TS
e
], x, C
′
x
1
(r
′′
,e
′
,v
′
,TS
′
P
,TS
′
e
)
Figure 3: S sends to P consumption data anonymously for load reporting.
Electricity theft is prevented by putting the smart me-
ter under seal. A trusted-platform-module (TPM)
detects (malicious) modifications in the smart meter
software and protects the key material (Petrlic, 2011)
(Lemay et al., 2007). Otherwise, Lemay et al. note
the high power consumption of a TPM in idle mode.
In our protocol we do not need such a fully-functional
TPM. Instead, we only require that the measured con-
sumption data can never be manipulated before signa-
ture S
1
is calculated. The smart meter must compute
S
1
in a trusted environment (aim 8).
To prevent counterfeiting of consumption data dur-
ing the load reporting protocol (e.g. to inflict damage
on the consumption forecasting), the hash function
H must operate in a trusted environment and hashes
the measured consumption data before it leaves the
trusted environment. A malicious customer has to fol-
low the protocol to persuade the energy provider to
accept the consumption data. This is a consequence
of the proof-of-knowledge property (see appendix 7).
4.4.2 Energy Provider
The energy provider acts maliciously by trying to cre-
ate a finely-grained energy consumption profile of
the customer. Our solution prevents this because of
the underlying group signature scheme. The monthly
submission of the aggregated energy consumption is
too coarse to create profiles.
4.4.3 Untrusted Smart Meter
The main motivation of an attacker with an untrusted
smart meter (e.g. a malicious competitor of the energy
provider) is to become part of the energy provider’s
grid to perturb the energy consumption forecast. We
assume that the attacker opens the smart meter or con-
structs a meter. A trusted environment no longer ex-
ists. The attacker can send the energy provider arbi-
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY
119

trary data but cannot create a valid signature for it. To
become a member of the grid, he must either have a
valid public / private key pair registered at the energy
provider or he must prove in zero-knowledge that he
has a valid signature for a ticket not yet consumed.
Even if the attacker has a public / private key pair, the
smart meter can only anonymously submit consump-
tion data every TS
log
minutes, which reduces the im-
pact of malicious data on the forecast (aim 3, aim 6).
5 IMPLEMENTATION &
BENCHMARK
We have implemented our solution on three different
hardware platforms. To measure performance on
the energy provider’s side, we run our protocol
on a standard server machine (Intel Xeon X3460
@2.8 GHz, 8 GB RAM, Windows Server 2008
R2 Enterprise). On the smart meter’s side, we do
not have a programmable smart meter available.
Instead, we evaluate our solution on a Linksys
WRT54GS wireless access point. The WRT54GS
has a Broadcom BCM4712 processor running at 200
MHz. The router is equipped with 32 MB RAM and
runs OpenWRT 10.03. We are of the opinion that this
hardware comes close to real smart metering devices
like the ZDUE-DSL MUC from Dr. Neuhaus. It
has a 210 MHz Atmel AT91SAM9260 processor,
32 MB RAM and runs an embedded Linux. Low
power consumption of smart meters is important.
According to the specification (Dr. Neuhaus, 2010),
the ZDUE-DSL MUC has a power consumption of
typically 2.2 Watt where the Linksys router has a
power consumption of 7.6 Watt idle and < 8 Watt at
full load.
We also run our protocol on a modified Seagate
FreeAgent Dockstar (Marvell Kirkwood 1.2 GHz,
128 MB RAM, Debian Linux, Kernel 2.6.32), which
has a better performance / power consumption ratio
(3.6 Watt idle, < 5 Watt at full load). The power
consumption was measured using the Voltcraft
Energy Logger 4000.
We set the bit length of the RSA modulus to
l
n
= 2048. The MPIR 2.2.1 bignum library (a fork of
GMPlib) is used to implement multi-precision integer
operations (Gladman, B. et al., 2010). If packets
must be encrypted or signed with the long-term
keys, we use RSA. SHA-1 characterized by a hash
size of 160 bit is employed as the hash function H.
Tickets are chosen in the interval (0,2
l
x
) with l
x
= 80.
The time lag interval is TS
log
= 10 minutes. We
randomly choose the signature creation time TS
P
in
the interval [0,44640) (one month) and randomly set
the time stamp TS to TS = TS
P
+ TS
log
+ [0,15]. The
expiration time stamp TS
e
is set to TS
e
= 201201
(concatenation of year and month). Other protocol
parameters are chosen regarding (Camenisch and
Groth, 2005) (l
E
= 404, l
e
= 60, l = 60). We run
our protocol 100 times and determine the average
runtime.
Table 1 shows the benchmark results for S and
P at each protocol stage. Unsurprisingly, the protocol
performs better on a PC than on the embedded plat-
forms. The results show that the protocol presented in
this paper is practical on real smart metering devices.
Even on low-performance hardware the protocol
performs fast enough to submit the consumption
data to the energy provider in a 15 minute window
(aim 7). The protocol calculations of P are not
time-consuming if a typical server machine is used.
We have tested our design only on a single core. If
e.g. all cores are used on the Intel Xeon X3460 CPU,
the performance would be eight times higher.
In real-world implementations one has to deal
with the problem that the smart meter can be (theo-
retically) identified by the underlying communication
protocols (e.g. IP / MAC address). The identity of
the smart meter is preserved but it is possible to link
packets coming from the same smart meter (and the
same sender’s address).
If the smart meter is connected with the internet
over DSL or GPRS, a connection reset can solve the
problem. The smart meter gets a new IP address and
new consumption data submissions are unlinkable
to former ones. On the one hand, if the smart meter
shares the internet connection, it is impractical to get
a new IP address before every submission. On the
other hand, internet providers usually automatically
reset the connection after 24 hours. A compromise
could be that the DSL connection is reset if there is
no traffic on the DSL connection.
If the smart meter communicates over a GPRS
connection using a public provider, a new connection
will be established for every new submission. This
also implicates a new IP address.
The Tor network (The Tor Project, 2011) can also
be used to obfuscate the sender’s address. Traffic is
routed in an encrypted way over intermediate nodes.
Although we have to shift some trust to the internet
service provider or intermediate nodes we don’t need
a TTP for key or group management (aim 9).
SECRYPT 2011 - International Conference on Security and Cryptography
120

Table 1: Performance comparison.
invoicing (S ) invoicing (P ) reporting (S ) reporting (P )
Server (Xeon X3460) 21 ms 19 ms 88 ms 65 ms
Dockstar (Marvell Kirkwood) 352 ms 324 ms 1469 ms 1080 ms
WRT54GS (Broadcom BCM4712) 4154 ms 3816 ms 17323 ms 12739 ms
6 RELATED WORK
The anonymous submission of consumption data
from a smart meter to another party for load report-
ing purposes has been previously studied by other
authors. We here compare their solution with our
solution.
M¨uller (M¨uller, 2010) gives a list of easily imple-
mentable recommendations to protect the customer’s
privacy.
1. Reducing the Temporal Resolution
The fewer data points are submitted to the energy
provider,the more difficult it is to identify the cus-
tomer. Sharp peaks in the diagram are flattened
and the energy consumption curve gets smoother,
showing only average values.
2. Aggregation of Intermediate Data
Data points of several days are accumulated at the
same time and sent to the energy provider.
3. Aggregation of Several Households
Like aggregation of intermediate data, data points
can be aggregated over several households.
Reducing the temporal resolution or aggregating the
data comes with the drawback of decreasing accuracy
and response time. The first two recommendations
contradict our no-delay-aim (aim 7). The aggregation
of several households increases the freshness of the
consumption data but comes with the drawback that
a TTP is needed between smart meter and energy
provider (contradicts aim 9). All smart meters send
the consumption data to the TTP, which authenticates
them, accumulates the data and forwards it to the
energy provider. The third party must be independent
from the energy provider to preserve the customer’s
privacy.
Petrlic (Petrlic, 2011) suggests a solution where
a smart meter communicates with the energy provider
over a collector. First, the smart meter encrypts the
consumption data with the public key of the energy
provider for load reporting. Second, it signs the
encrypted message using a pseudonym and submits
the signed and encrypted message to the collector.
The collector verifies the signature, removes the
signature and forwards the encrypted data signed by
a MAC to the energy provider.
This solution requires a TTP between smart meter
and energy provider. Another trusted party is needed
to manage grid membership (contradicts aim 9).
Garcia and Jacobs suggest to use homomorphic
encryption (Garcia and Jacobs, 2010), where each
smart meter directly submits the consumption data to
the energy provider without using a collector (they
use a collector but this is part of the energy provider).
The smart meter separates consumption data (every
measurement) into N samples, where N is the number
of smart meters in a neighbourhood. Every smart
meter sends N− 1 samples in an encrypted way to the
neighbouring smart meters over the energy provider.
All smart meters accumulate the consumption data
(e.g. the first smart meter accumulates the first sample
of all N consumption data, the second smart meter
accumulates the second sample of all N consumption
data...) and send the result back to the energy
provider. A TTP is needed to create smart meter
certificates (contradicts aim 9). Furthermore, a lot of
encrypted messages have to be exchanged, especially
if the neighbourhood is big. This fact makes the
protocol inefficient.
7 CONCLUSIONS
The contribution of this paper consists in offering a
new protocol for smart meters, which reports the elec-
tricity consumption back to their energy providers
for the sake of load reporting and invoicing. De-
spite the fact that the customer’s privacy is preserved,
the protocol still allows the detection of unregistered
smart meters and prevents spamming and replay at-
tacks. Compared with other solutions, a TTP is not
needed for key or group management, which makes
our solution interesting for real world implementa-
tions. The security of the protocol is based on the
well-investigated strong RSA assumption and the ran-
dom oracle model. Benchmark results prove that the
protocol is practical. The protocol is not restricted to
electrical smart meters and can easily be adapted to
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY
121

other sensor networks.
ACKNOWLEDGEMENTS
The author would like to thank Klaus M¨uller for con-
tributing the data of figure 1.
REFERENCES
Berg Insight (2010). Worldwide installed base of smart
electricity meters will reach 302.5 million units in
2015.
Camenisch, J. and Groth, J. (2005). Group Signatures: Bet-
ter Efficiency and New Theoretical Aspects. In pro-
ceedings of SCN ’04, LNCS series, pages 120–133.
Springer.
Camenisch, J. and Lysyanskaya, A. (2003). A Signature
Scheme with Efficient Protocols. In Cimato, S., Per-
siano, G., and Galdi, C., editors, Security in Commu-
nication Networks, volume 2576 of Lecture Notes in
Computer Science, pages 268–289. Springer Berlin /
Heidelberg. 10.1007/3-540-36413-7 20.
Camenisch, J. and Stadler, M. (1997). Proof Systems for
General Statements about Discrete Logarithms. Tech-
nical Report 260, Institute for Theoretical Computer
Science, ETH Z¨urich.
Dr. Neuhaus (2010). MUC-Controller zur Fernauslesung
von Haushaltsz¨ahlern via DSL – Specification.
Fiat, A. and Shamir, A. (1987). How to prove your-
self: Practical solutions to identification and signa-
ture problems. In Odlyzko, A. M., editor, Advances in
Cryptology – CRYPTO ’86, volume 263, pages 186–
194. Springer Verlag.
Garcia, F. D. and Jacobs, B. (2010). Privacy-friendly
energy-metering via homomorphic encryption. In
et al., J. C., editor, In 6th Workshop on Security
and Trust Management (STM 2010), Lecture Notes in
Computer Science. Springer Verlag.
German Federal Ministry of Justice (2005). Gesetz ¨uber die
Elektrizitts- und Gasversorgung (Energiewirtschafts-
gesetz - EnWG), Paragraph 21b.
German Federal Ministry of Justice (2008). Erneuerbare-
Energien-Gesetz, Paragraph 2.
Gladman, B. et al. (2010). MPIR - Multiple Precision Inte-
gers and Rationals.
Groth, J. (2005). Non-interactive zero-knowledge argu-
ments for voting. In In proceedings of ACNS ’05,
LNCS series, pages 467–482. Springer-Verlag.
Lemay, M., Gross, G., Gunter, C. A., and Garg, S. (2007).
Unified architecture for large-scale attested metering.
In in Hawaii International Conference on System Sci-
ences. Big Island. ACM.
McDaniel, P. and McLaughlin, S. (2009). Security and Pri-
vacy Challenges in the Smart Grid. IEEE Security and
Privacy, 7(3):75–77.
M¨uller, K. J. (2010). Gewinnung von Verhaltensprofilen am
intelligenten Stromz¨ahler. Datenschutz und Daten-
sicherheit, 6:359–364.
M¨uller, K. J. et al. (2011). Volksz¨ahler - Smart Meter for
Self-Construction.
Petrlic, R. (2011). A privacy-preserving concept for smart
grids. In 18. DFN Workshop ”Sicherheit in vernetzten
Systemen”.
Pointcheval, D. and Stern, J. (1996). Security proofs for
signature schemes. In Maurer, U., editor, Advances in
Cryptology – EUROCRYPT ’96, volume 1070, pages
387–398. Springer Verlag.
Rabin, J. O. and Shallit, J. (1985). Randomized algorithms
in number theory. Technical report, University of
Chicago, Chicago, IL, USA.
Schnorr, C.-P. (1991). Efficient Signature Generation by
Smart Cards. Journal of Cryptology, 4(3):161 – 174.
The Tor Project (2011). Tor: anonymity online.
APPENDIX
This section contains a short summary of some cryp-
tographic building blocks that we use in this pa-
per. In the first part, we explain the Groth commit-
ment scheme and give a short introduction to zero-
knowledge protocols in the second part. At the end,
we explain how to prove in zero-knowledge that a se-
cret number fulfils an inequality.
A. Commitment Schemes
A non-interactive commitment scheme consists of
three algorithms, ComSetup, Commit and ComOpen.
The hiding property ensures that a commitment C
x
to
x does not reveal any information about x, whereas the
binding property ensures that C
x
cannot be opened to
another value x
′
. For our solution, we choose the in-
teger commitment scheme of Groth (Groth, 2005).
ComSetup: First generate the parameters of the com-
mitment scheme. Set l
n
as the bit length of a given
special RSA modulus n and l as the bit-length of
the security parameter. Randomly choose a generator
h ∈
R
QR
n
and k exponents α
i
(for i = 1,. ..,k) of bit
length l
n
+ l. Then compute g
i
= h
α
i
(for i = 1,.. . ,k).
Commit: To commit integers (m
1
,. ..,m
k
) of bit
length l
m
, choose a random integer p of bit length
l
n
+ l and compute C = g
m
1
1
·· · g
m
k
k
h
p
mod n. Al-
gorithm Commit outputs the commitment C together
with auxiliary information p to open the commitment.
Open: To open a commitment C, compute C
′
=
g
m
′
1
1
·· · g
m
′
k
k
h
p
′
mod n for input integers (m
′
1
,. ..,m
′
k
)
and p
′
. Check whether C = C
′
.
SECRYPT 2011 - International Conference on Security and Cryptography
122

B. Zero-knowledge Proofs of Knowledge
With the help of a proof of knowledge a prover P
can convince a verifier V that he knows a solution
for a mathematical hard problem. On the one hand,
an honest P can always convince V (completeness
property); on the other hand, a dishonest P will fail
to convince V with overwhelming probability if he
attempts to cheat without knowing the correct solu-
tion (soundness property). A zero-knowledge proof
of knowledge ZPK is a proof of knowledge where V
obtains no further information from P other than the
fact that P knows the solution of the underlying math-
ematically hard problem. E.g.:
ZPK[(ω) : x = g
ω
] (2)
In ZPK (2) P proves to V the knowledge of the
secret value w where w fulfils the relationship x = g
w
.
Secrets are marked in Greek characters. x and g are
public values. Determining w by only knowing x and
g is a mathematical hard problem.
ZPKs are usually implemented by Σ-protocols,
which are based on the Schnorr protocol (Schnorr,
1991), an interactive, challenge-response protocol.
To achieve a high level of security the protocol has to
be executed several times, which decreases protocol
performance. The Fiat-Shamir heuristic (Fiat and
Shamir, 1987) (Pointcheval and Stern, 1996) and
the random oracle model can be used to execute
the protocol in a non-interactive way so that a ZPK
becomes a signature proof of knowledge (SPK).
Several predicates can be concatenated by logical
AND/OR operators to model more complex proofs.
C. Inequality Proofs
Let C
w
i
= g
w
i
h
p
i
be Groth Commitments with inte-
gers w
i
for i = 1,...,3. With the relation g
w
3
h
p
3
=
C
w
2
w
1
h
p
3
h
−p
1
w
2
for w
3
= w
1
· w
2
we can prove in zero-
knowledge that w
3
is the product of w
1
and w
2
:
ZPK
((ω
i
,ρ
i
)
3
i=1
,ω
2
· ρ
1
) :
3
V
i=1
C
w
i
= g
ω
i
h
ρ
i
∧
1 = C
ω
2
ω
1
g
−ω
3
h
−ρ
1
ω
2
(3)
Lagrange’s Four-Square Theorem says that every
non-negative number w can be decomposed into a
sum of four square numbers w
1
,..., w
4
with w =
(w
1
)
2
+ (w
2
)
2
+ (w
3
)
2
+ (w
4
)
2
. If w has the form
4w
′
+ 1, Rabin and Shallit showed that even three
squares w
2
1
,. ..,w
2
3
are enough to decompose w in
probabilistic polynomial time (Rabin and Shallit,
1985). To prove that 4w
′
+ 1 ≥ 0 where w
′
is a pos-
itive integer, we decompose 4w
′
+ 1 into a sum of
three squares for a committed value w
′
and prove that
4w
′
+ 1 = (w
1
)
2
+ (w
2
)
2
+ (w
3
)
2
.
ZPK
(ω
′
,ρ,ω
1
,ω
2
,ω
3
) : C
w
= g
ω
′
h
ρ
∧
4ω
′
+ 1 = (ω
1
)
2
+ (ω
2
)
2
+ (ω
3
)
2
(4)
Proof (4) can be realized using the Σ
GSP
-protocol and
with the help of proof (3) (Groth, 2005).
PRIVACY-PRESERVING SMART METERING WITHOUT A TRUSTED-THIRD-PARTY
123
