
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS
APPLICATIONS
Nabil Fakhfakh, Fr´ed´eric Pourraz and Herv´e Verjus
LISTIC Laboratory, University of Savoie, Chemin de Bellevue, Annecy-Le-Vieux, France
Keywords:
QoS aggregation, e-Business applications, Satisfaction degree measurement, The Choquet Integral.
Abstract:
In e-business applications, enterprises build their processes to achieve their business goals. One of the archi-
tectural models of e-business applications is a service-based approach. This approach consists in orchestrating
the e-services offered by one or several enterprises partners in order to build the desired business processes.
It is important for the enterprises to ensure client satisfaction in order to be more attractive and more com-
petitive. Quality of Service has a significant impact on client satisfaction. Therefore, clients need e-business
applications with high Quality of Service to be satisfied. In this context, we propose in this paper an approach
that allows clients to measure the satisfaction degree of the services orchestration. This approach takes into
account client’s preferences on QoS attributes and their related dependencies in the measurement of the satis-
faction degree. We treat two examples of services orchestration and show how does the measured satisfaction
allow the client to choose the best one.
1 INTRODUCTION
Electronic business or e-business can be defined as
the use of the technology of the Web to do business.
There is a variety of e-business models. Among them,
we found the Business to Client (B2C) and Business
to Business to Client (B2B2C) (Qi and Huang, 2005).
Enterprises based on these models put much impor-
tance to client’s satisfaction in the development of
their e-business applications. For this purpose, en-
terprises have to provide e-business applications with
high Quality of Service (QoS) to be more competitive
and to reach client’s satisfaction. QoS has a signif-
icant impact on client’s satisfaction and it is closely
related to this latter. In this paper, we propose a
method to measure client’s satisfaction related to QoS
of the e-business application. We are interesting in e-
business applications supported through orchestrated
e-services.
When developing their e-business applications,
enterprises aim to respect client’s QoS expectations
specified on the services orchestration. QoS expecta-
tions are defined by the upper and lower bounds of
the QoS levels that the services orchestration must
meet to guarantee client’s satisfaction. The upper QoS
level’s bound is denoted desired QoS level (Parasura-
man et al., 1994), and represents the QoS level that
satisfy the best the client. Whereas, the lower QoS le-
vel’s bound is denoted adequate QoS level (Parasur-
aman et al., 1994), and represents the minimum QoS
level that satisfy the client. We denote also the mea-
sured QoS level at run-time and on client’s side by
the perceived QoS level (Parasuraman et al., 1994).
However, during services’ life cycle, perceived QoS
attributes values of the services may change. This
leads to a variation of the perceived QoS level of the
services orchestration into the range of QoS expec-
tations. Besides, the client’s satisfaction of the e-
business application supported through this services
orchestration will be impacted. Therefore, clients ex-
ploiting the e-business application need to know how
much they are satisfied in terms of QoS.
Various works dealing with evaluation of ser-
vices orchestration’s QoS attributes exist in the litera-
ture (Cardoso et al., 2002; Jaeger et al., 2005; Rosen-
berg, 2009). Currently, none approach supports dif-
ferent QoS attributes simultaneously in order to pro-
vide a high level information about the QoS of the
overall services orchestration. The satisfaction degree
of services orchestration is a such high level infor-
mation, which facilitates the interpretation of QoS at-
tributes values of the services orchestration.
To measure the satisfaction degree of services or-
chestrations, we will use a Multi-Criteria Decision
Making (MCDM) method that takes only client’s
preferences on the QoS attributes as inputs, neces-
100
Fakhfakh N., Pourraz F. and Verjus H..
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS.
DOI: 10.5220/0003519401000110
In Proceedings of the International Conference on e-Business (ICE-B-2011), pages 100-110
ISBN: 978-989-8425-70-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

sary to construct the QoS aggregation model. More-
over, we consider that there are dependencies be-
tween clients’ preferences over QoS attributes. There-
fore, we use an aggregation operator, which is able
to support preferential dependencies. The method we
choose is the MACBETH method (Costa et al., 2005)
extended to the 2-additive Choquet Integral (Cliville
et al., 2007; Mayag et al., 2010).
The remainder of this paper is organized as fol-
lows. Section 2 discusses related work. In Section 3,
we present our approach for the measurement of ser-
vices orchestration satisfaction degree. Section 4 de-
tails a use case of the satisfaction degree measure,
while Section 5 concludes the paper.
2 RELATED WORK
In this Section, we compare our approach to the ex-
isting ones in 2.1, and we overview related works on
QoS evaluation for services orchestrations in 2.2.
2.1 QoS Aggregation Efforts
(Menasc´e, 2003) presents an automatic QoS con-
troller for e-commerce sites. The QoS controller
monitors the site’s workload and determine the best
configuration that meet the site’s QoS requirements.
It executes an algorithm that takes into account the
observed workload, the desired QoS levels, to deter-
mine configuration parameters. The algorithm tries
to find the configuration parameters that maximise a
QoS metric defined as:
QoS =
n
∑
i=1
w
k
× f
k
(∆
k
)
where n is the number of QoS attributes being aggre-
gated, w
k
is a relative importance weight assigned to
QoS attribute k (
∑
n
i=1
w
k
= 1), ∆
k
is a relative devia-
tion of the QoS attribute k defined in a way that the
relative deviation is positive when the QoS attribute
exceeds its requirement and negative otherwise, and
f
k
() is an increased function of ∆
k
. The authors as-
sume that the relative weights (w
k
) are assigned by
site management. In our mind, assigning directly
weights to QoS attribute is not a trivial task, espe-
cially when we have several QoS attributes. In our
approach,we need only decision makerpreferencesto
determine aggregation model parameters. Moreover,
the authors use linear transformation to normalize ∆
k
(i.e., to have a value in the interval [0,1]). The bet-
ter the normalized value is (tends to 1), the better the
QoS requirement is met. Therefore, the normalized
value represents the satisfactory value to the related
QoS attribute. Using linear transformation is not very
accurate to model the real satisfaction of the client.
For example, the model of the availability’s satisfac-
tion can be a curve. In our approach (see Section 3),
we do not use linear transformation to normalize QoS
attributes but we compute normalized values based on
informations given by the client (see Figure 6).
In (Szydlo and Zielinski, 2008), authors present
a method for adaptive quality control of services or-
chestrations. The goal of the method is to satisfy
client requirements and to preserve his budget by
changingSLA during execution. The method is based
on a QoS controller that monitors deviation of per-
ceived QoS attributes values from the agreed in the
SLA, and on this basis, services to be invoked are
selected. The client choose a set of SLAs he is in-
terested in, and the system selects the SLA with the
best fitness function and price. The fitness function
is defined as a weighted mean of QoS attributes val-
ues. Authors uses the Analytical Hierarchy Process
(AHP) (Forman and Selly, 2001) method to build the
aggregation model. However, the AHP method does
not take into account dependencies between pref-
erences on QoS attributes since it is based on the
weighted mean operator.
(Herssens et al., 2008) presents an approach for
services selection. The approach is based on a QoS
model that enables users to express their requirements
and providers to represent their services’ QoS. The
model also allows to represent priorities (preferences)
and dependencies between QoS attributes. The selec-
tion mechanism relies on a MCDM method that takes
into account relationships and dependencies between
QoS attributes. The MCDM used is the Choquet
Integral. However, authors assume that the service
provider specifies the dependencies and their effects
(i.e., positive or negative) that can exist between QoS
attributes. In general, dependencies between QoS at-
tributes are due to the techniques used to improve one
or several QoS attributes. In other words, depend-
ing on the technique used, the improvement of a QoS
attribute can affect other QoS attributes in a positive
or negative way. However, we can obtain the desired
QoS (that fit the best the expectations) by using ap-
propriate techniques. In our approach, we assume
that dependencies exist between client’s preferences
over the set of QoS attributes and not between QoS
attributes variables. Authors also use linear transfor-
mation to normalize QoS attributes. As we discussed
above, this assume that the satisfaction of the client is
linear which is not necessarily the case. Our approach
takes only client’s preferences as inputs and allows to
generate normalized QoS attributes values and aggre-
gation operator parameters.
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS
101

In our previous work (Fakhfakh et al., 2011),
we have used Measuring Attractiveness by a
Categorical-Based Evaluation TecHnique (MAC-
BETH) method (Costa et al., 2005) based on the
weighted mean operator to aggregate QoS attributes
values. The MACBETH method allows us to ex-
press QoS attributes in the same scale and determine
the weights of the weighted mean operator. The ad-
vantage of MACBETH method is that its inputs are
only restricted to the informations provided by the
client (i.e., preferences and their intensity over QoS
attributes) and does not make any other assumption.
We used this kind of method because we consider
that the satisfaction is client specific (i.e., varies from
one client to another) and depends on client prefer-
ences. However, the major limitation of the MAC-
BETH method is that it assumes that client’s prefer-
ences on QoS attributes are independent. For exam-
ple, let us consider three QoS attributes : response
time, reliability and availability. One client may ex-
press that he prefers more the availability than the re-
sponse time when the reliability is good. However, he
prefers more the response time than the availability
when the reliability is bad. These kinds of informa-
tion is not supported by MCDM methods based on a
weighted mean operator due to its independence as-
sumption. For this purpose, we use a MCDM method
based on the Choquet Integral operator.
In this paper, we will use an extension of the
MACBETH method to the 2-additive Choquet Inte-
gral (Cliville et al., 2007; Mayag et al., 2010) that
permits to take into account dependencies between
client’s preferences.
2.2 QoS Evaluation for Services
Orchestrations Approaches
Various approaches have been proposed to compute
each QoS attribute value independently for services
orchestration (e.g., giving response time values for all
services composing the orchestration, how to com-
pute the response time of the overall orchestration ?).
These approaches can be classified in two categories:
probabilistic model-based approaches (Gallotti et al.,
2008)(Satoand Trivedi, 2007)(Cortellessaand Grassi,
2007)(Zhong and Qi, 2006) and workflow pattern-
based approaches (Jaeger et al., 2005) (Rosenberg,
2009)(Cardoso et al., 2002) (Coppolino et al., 2007).
The first category of approaches allowing to com-
pute QoS attributes values of services orchestration
is based on probabilistic models. It consists in
transforming the services orchestration model into a
probabilistic model (e.g., Continuous Time Markov
Chain (CTMC) model (Gallotti et al., 2008)(Sato
and Trivedi, 2007) or Discrete Time Markov Chain
(DTMC) (Cortellessa and Grassi, 2007) or Stochas-
tic Petri Nets (SPN)(Zhong and Qi, 2006)). Then,
the probabilistic model is annotated with QoS at-
tributes values. Finally, these approaches use tools
like PRISM (Gallotti et al., 2008) or SPNP (Zhong
and Qi, 2006) to compute each QoS attribute value of
services orchestration. The major drawback of these
approaches is that they only support reliability and/or
response time (see Table 1).
The second category consists in defining aggrega-
tion rules of QoS attributes for each pair of workflow
patterns (van der Aalst et al., 2003). A pair of work-
flow pattern is composed of ”one split pattern” (e.g.,
AND-split) and ”one join (synchronisation) pattern”
(e.g., XOR-join) except the sequence and the loop
patterns, which are individually considered. The ad-
vantage of workflow pattern-based approaches is that
they support larger set of QoS attributes (see Table 1).
Moreover, they are extensible: (i) more workflow
patterns could be added and (ii) new QoS attributes
could be integrated. For that reason, in our approach,
we will exploit a workflow pattern-based approach.
However, when changes affect positively or neg-
atively some QoS attributes values, it becomes dif-
ficult to estimate how much the whole orchestration
fits client’s expectations and satisfaction ; especially
when we have several QoS attributes. Thus, it would
be useful to have a high-level information. We de-
fine this information as the services orchestration sat-
isfaction degree. This could be done by aggregating
the QoS attributes values to provide a sole aggregated
value that measures the satisfaction degree of the ser-
vices orchestration. To this end, we propose to use a
MCDM method.
3 AGGREGATION PROPOSAL
In this section, we introduce our proposal for aggre-
gating QoS attributes values in order to provide a
measure of the satisfaction degree of services orches-
tration according to client’s QoS expectations. We op-
erationalize the satisfaction degree as the score out
of 1 that represents how much the perceived QoS
level, for the overall services orchestration, respects
QoS expectations (i.e., client satisfaction). It takes
the value of 0 if the perceived QoS level is less than
or equal to the adequate QoS level, and the value of
1 if the perceived QoS level is greater than or equal
to the desired QoS level. As we said above, QoS ex-
pectations are defined by means of desired and ade-
quate QoS levels. We define a QoS level as a vector
of QoS attributes values denoted (q
1
, ..., q
n
) , where
ICE-B 2011 - International Conference on e-Business
102

Table 1: Aggregation Categories vs Supported QoS Attributes.
Category Research work Supported QoS attributes
Probabilistic model-based approaches
(Gallotti et al., 2008) Execution time, reliability
(Cortellessa and Grassi,
2007)
Reliability
(Sato and Trivedi, 2007) Response time, reliability
(Zhong and Qi, 2006) Reliability
Workflow pattern-based approaches
(Jaeger et al., 2005) Throughput, response time,
cost, availability, reputation,
security
(Rosenberg, 2009) Throughput, response time,
cost, availability, reputation,
security , scalability, accu-
racy, robustness
(Cardoso et al., 2002) Response time, cost, relia-
bility, fidelity
(Coppolino et al., 2007) Reliability
Figure 1: Principe of the Aggregation Approach.
q
j, 1≤ j≤n
is the j
th
QoS attribute value. Therefore, the
desired QoS level is a vector of the desired QoS at-
tributes values, while the adequate QoS level is a vec-
tor of the adequate QoS attributes values. If the client
knows the services involved in the services orchestra-
tion, he may define his individual QoS expectations
on each service. In this case, QoS expectations on the
services orchestration can be computed by applying a
workflow pattern-based aggregation approach.
Our approach is composed of two phases (see Fig-
ure 1): in the first phase, we use workflow patterns
aggregation rules, while in the second phase we use
a MCDM method based on the 2-additive Choquet
Integral. At execution time, each service S
i
has a
perceived QoS level (q
1
, ..., q
n
)
Si
(obtained from per-
ceived QoS attributes values). Given these perceived
QoS levels of all orchestrated services, they are firstly
aggregated in phase 1 using workflow patterns aggre-
gation rules. This results in one perceived QoS level
of the services orchestration (q
1
, ..., q
n
)
orch
(see Fig-
ure 1). Then, the QoS attributes values of this per-
Figure 2: B2C Services Orchestration.
ceived QoS level will be aggregated in phase 2 us-
ing a MCDM method. This provides us a sole and
consolidated value, which is the satisfaction degree
of the services orchestration. Before detailing these
two phases, we present a car insurance e-business ap-
plication supported through a services orchestration
described in Figure 2. We will use this B2C services
orchestration model to illustrate our approach here-
after.
The process starts by asking some informations to
the user (user age, driving license, car typeand model,
etc.). Such informations are firstly analysed for a de-
cision: either the quotation request is accepted, either
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS
103

Table 2: Aggregation Rules (Rosenberg, 2009)(Cardoso et al., 2002).
Response Time Reliability Availability
Sequence
∑
n
i=1
q
rt
(s
i
)
∏
n
i=1
q
rel
(s
i
)
∏
n
i=1
q
av
(s
i
)
Loop q
rt
(s
i
) ∗ c q
rel
(s
i
)
c
q
av
(s
i
)
c
AND-AND max(q
rt
(s
1
), ..., q
rt
(s
n
))
∏
n
i=1
q
rel
(s
i
)
∏
n
i=1
q
av
(s
i
)
XOR-XOR
∑
n
i=1
p
i
.q
rt
(s
i
)
∑
n
i=1
p
i
.q
rel
(s
i
)
∑
n
i=1
p
i
.q
av
(s
i
)
a
c denote the number of occurring loops
b
p
i
the probabilities of the outgoing branches for XOR-XOR
it is immediately rejected. When accepted, a quota-
tion is established taken into account user informa-
tions provided. Then, a commercial offer is pack-
aged comprising the car insurancequotationand some
commercial and promotional offers (life insurance,
house insurance, etc.). The commercial offer is sent
to the user.
Hereafter, we assume that QoS expectations (i.e.,
desired and adequate QoS levels) and measurements
(i.e., perceived QoS attributes values) are respectively
given by the client and a monitoring system (QoS at-
tributes measurement is out of the scope of this pa-
per).
3.1 Phase 1: Aggregation based on
Workflow Patterns Rules
In the first phase (see Figure 1), we use aggregation
rules based on workflow patterns (see section 2.2)
to compute each QoS attribute value of the services
orchestration. This consists in applying step-by-step
rules in order to aggregate QoS attributes values. The
applied rules are those corresponding to the pairs of
workflow patterns used in the services orchestration
model. Beginning from the most nested pair of work-
flow pattern, the orchestration modelis parsed and ag-
gregation rules for each QoS attribute in the perceived
QoS level are progressively applied. This terminates
when the whole services orchestration is reduced to
a single node (Figure 3). The resulted QoS attributes
values of the resulting node compose the perceived
QoS level of the services orchestration. This approach
is relevant for each QoS attribute that has aggregation
rules for the pairs of workflow patterns. We will de-
tail this phase through the illustrative example of the
services orchestration described in Figure 2.
For simplification purpose, we will consider a re-
stricted set of three QoS attributes values: response
time (q
rt
), reliability (q
rel
) and availability (q
av
). The
aggregation rules for each pair of workflow patterns
and for each QoS attribute are summarized in Table 2.
The first step consists in checking the most nested
workflow pattern which is the sequence pattern be-
tween S
4
, S
5
and S
6
in Figure 3a. Then, we apply the
respective aggregation rule from Table 2. The QoS
attributes values computation of this composition pat-
tern gives :
q
rt
(S
4,5,6
) = q
rt
(S
4
) + q
rt
(S
5
) + q
rt
(S
6
)
q
rel
(S
4,5,6
) = q
rel
(S
4
).q
rel
(S
5
).q
rel
(S
6
)
q
av
(S
4,5,6
) = q
av
(S
4
).q
av
(S
5
).q
av
(S
6
)
Thus, the orchestration model is reduced to that
given in Figure 3b. Then, taking into account the
reduced orchestration model, the next workflow pat-
tern to be considered is the sequence pattern of S
3
and
S
4,5,6
. The QoS attributes values computation of this
composition pattern gives :
q
rt
(S
3,4,5,6
) = p
1
.q
rt
(S
4,5,6
) + p
2
.q
rt
(S
3
)
q
rel
(S
3,4,5,6
) = p
1
.q
rel
(S
4,5,6
) + p
2
.q
rel
(S
3
)
q
av
(S
3,4,5,6
) = p
1
.q
av
(S
4,5,6
) + p
2
.q
av
(S
3
)
The obtained orchestration model from this step is
composed of three nodes structured in sequence (Fig-
ure 3c). By aggregatingQoS attributes values of these
three nodes in sequence, we obtain:
q
rt
(S
1,2,3,4,5,6
) = q
rt
(S
1
) + q
rt
(S
2
) + q
rt
(S
3,4,5,6
)
q
rel
(S
1,2,3,4,5,6
) = q
rel
(S
1
).q
rel
(S
2
).q
rel
(S
3,4,5,6
)
q
av
(S
1,2,3,4,5,6
) = q
av
(S
1
).q
av
(S
2
).q
av
(S
3,4,5,6
)
This resulting values are those that compose the
perceived QoS level of the whole services orches-
tration (q
rt
, q
rel
, q
av
)
orch
and will be the input of the
phase 2 (Figure 1).
3.2 Phase 2: Aggregation using the
2-Additive Choquet Integral
The goal of this phase is to aggregate different values
in the perceived QoS level of the services orchestra-
tion (i.e., (q
rt
, q
rel
, q
av
)
orch
) in order to obtain a mea-
sure of the satisfaction degree of the services orches-
tration (q
orch
) (see Figure 1). This measure allows us
ICE-B 2011 - International Conference on e-Business
104

(a) Step 1. (b) Step 2. (c) Step 3. (d) Step 4.
Figure 3: Workflow Pattern-Based Aggregation Steps.
Table 3: Example of QoS Levels Illustrating Dependencies.
Response Time Reliability Availability
A 0.7 0.8 0.9
B 0.8 0.75 0.9
C 0.8 0.75 0.5
D 0.7 0.8 0.5
to detect positive or negative deviations that affect the
perceivedQoS levelof the services orchestrationfrom
one execution to another. It is also useful to compare
several services orchestrations having the same busi-
ness goal.
As we discussed above (see Section 2.1), the
weighted mean operator considers that the client’s
preferences on the QoS attributes are independent.
However, they could be some dependencies between
them. As an example, let us consider four QoS lev-
els denoted A, B, C and D presented in Table 3. One
client may express that he prefers the reliability to the
response time when the availability is good (i.e., he
prefers A to B). On the other hand, the same client
may say that he prefers the response time to the relia-
bility when the availability is bad (i.e., he prefers C to
D). These two expressions of preference leads to the
following inequalities:
q
orch
((0.7, 0.8, 0.9)) > q
orch
((0.8, 0.75, 0.9)
q
orch
((0.7, 0.8, 0.5)) < q
orch
((0.8, 0.75, 0.5)
These preferences cannot be modelled by a
weighted mean operator. Indeed, the first inequal-
ity implies that reliability is more important than re-
sponse time, whereas the second inequality implies
exactly the opposite. This means that the importance
between the reliability and the response time depends
on the satisfaction of the availability. This case is an
example of preferential dependencies between crite-
ria and is not supported by the weighted mean oper-
ator (see (Grabisch and Labreuche, 2005; Grabisch
and Labreuche, 2008) for more details about criteria
dependencies).
For this reason, we have choose the 2-additive
Choquet Integral, which takes into account preferen-
tial dependencies between criteria.
The 2-additive Choquet Integral operator is de-
fined by the following aggregation formula:
q
orch
=
n
∑
i=1
ν
i
.q
i
−
1
2
n
∑
j=1
I
ij
.|q
i
− q
j
| (1)
and involves 2 types of parameters :
• Shapley parameters ν
i
, which are the weights of
each QoS attribute, with
∑
n
i=1
ν
i
= 1,
• Interaction parameters I
ij
that quantify mutual in-
teraction between criteria i and j, with I
ij
∈ [−1, 1]
and
ν
i
−
1
2
∑
n
j=1
|I
ij
|
≥ 0 ∀i ∈ [1, n] and j 6= i.
These parameters (I
ij
) may be:
– positive, which implies that there is a contradic-
tion between the pairs of criteria. So the aggre-
gated value of QoS attributes (q
orch
) decreases,
– negative, which implies that there is a positive
synergy between the pairs of criteria. Thus, the
aggregated value of QoS attributes (q
orch
) in-
creases,
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS
105

– null, which implies that the pairs of criteria are
independent. Therefore, the 2-additive Choquet
Integral becomes equivalent to the weighted
mean operator.
We use an extension of the MACBETH
method (Costa et al., 2005) to construct the model of
the 2-additive Choquet Integral (Cliville et al., 2007;
Mayag et al., 2010), as it takes as inputs only client’s
preferences. It is based on pairwise comparison of
situations made by the decision maker, who is the
client in our case. The MACBETH method comprises
four main steps (Figure 4). As MACBETH method is
based on the weighted mean operator, only the two
latter steps differ since the aggregation operator and
its related parameters are different.
3.2.1 Context Definition Step
The first step consists in identifying the criteria that
the comparison will be based on. In our context, crite-
ria are QoS attributes (e.g., response time, reliability,
availability). Secondly, situations that will be com-
pared are defined. In our case, situations are repre-
sented by QoS levels (i.e., vectors of QoS attributes
values).
If we consider the example of the e-business pro-
cess cited above, the situations to be compared are the
perceived QoS level of the overall services orches-
tration (q
rt
, q
rel
, q
av
)
orch
(i.e., resulting from work-
flow patterns aggregation rules) in addition to the
desired and adequate QoS levels of the overall ser-
vices orchestration. The desired and adequate QoS
levels are called reference situations in MACBETH
method. They are denoted respectively as good situa-
tion and neutral situation. After normalization, these
two situations correspond respectively to the situa-
tions (1, 1,1) and (0, 0, 0), for which the associated
satisfaction degrees are respectively 1 and 0. So, the
client (the decision maker) has to compare the follow-
ing situations:
S
good
orch
= (q
good
rt
, q
good
rel
, q
good
av
)
S
perceived
orch
= (q
rt
, q
rel
, q
av
)
orch
S
neutral
orch
= (q
neutral
rt
, q
neutral
rel
, q
neutral
av
)
Note that if we have more situations (e.g., previ-
ous services orchestration executions), we can include
them in the definition context. This provides more
accurate models of QoS attributes normalization (see
Section 3.2.2).
Table 4: Preferences and Preference Strengths for Response
Time.
q
rt
Good S
perceived
Neutral
Good No h
1
a
P
S
perceived
No h
2
Neutral No
a
0=null, 1=very weak, 2=weak, 3=moderate, 4=strong,
5=very strong, 6=extreme
3.2.2 The QoS Attributes Normalization Step
In this step, the goal is to normalize QoS attributes
values. We do not use linear transformations to nor-
malize them, but we preferably exploit informations
provided by the client. For that purpose, the client
(decision maker) uses his expertise to judge given sit-
uations and fulfill the matrix of judgements like the
one given in Table 4. Firstly, he is asked for each QoS
attribute about his preferences between pairs of situ-
ations (including the two reference situations). If the
client prefers situation S
i
to S
j
for a QoS attribute k,
this is noted as follows:
S
i
≻S
j
and means that for the normalized QoS attributes val-
ues q
i
k
> q
j
k
. This is mapped in Table 4 into the clas-
sification of the situations by their order of preference
depending on the values of the QoS attribute k.
Secondly, the client expresses his strengths of
preference about the difference of attractiveness be-
tween the same situations. The strengths of pref-
erence are characterized with seven levels in the
MACBETH method: 0=null, 1=very weak, 2=weak,
3=moderate, 4=strong, 5=very strong, 6=extreme
(see Table 4). If the client is not able to give his
strengths of preference but only his preferences, this
is noted as positive or more shortly P. For a QoS
attribute k, the client prefers the situation S
i
to S
j
with a difference of attractiveness characterized by a
strength h
m
∈ {0, ..., 6} i.e.,
S
i
≻
h
m
S
j
This is equivalent to :
q
i
k
− q
j
k
= h
m
.α (2)
where α is a coefficient necessary to meet the con-
dition q
i
k
and q
j
k
∈ [0, 1].
When all the strengths of preference between sit-
uations are provided and the matrix of judgements is
fulfilled (e.g., see Table 4), a system of equations can
be extracted. Each strength of preference expressed
on pair of situations gives an equation under the form
of equation 2. By solving this system of equations,
ICE-B 2011 - International Conference on e-Business
106

Figure 4: The Main Steps of MACBETH Method.
the normalized QoS attributes values are quantified in
the interval [0,1].
Example: for the strengths of preferences ex-
pressed in Table 4 for the response time, the system
of equations is the following:
(q
good
rt
= 1); q
good
rt
− q
rt
= 1 − q
rt
= h
1
.α
(q
neutral
rt
= 0); q
rt
− q
neutral
rt
= q
rt
− 0 = h
2
.α
In the above system, the unknown variables are q
rt
and α, as h
1
, h
2
∈ {0, ..., 6} and are given by the
client. So, the system of equations can be solved and
the normalized response time of the perceived QoS
level can be computed. Note that the same procedure
is established for each QoS attribute (i.e., reliability
and availability).
3.2.3 Model Parameters’ Determination Step
In this step, we have to determine the parameters
of the 2-additive Choquet Integral, which are ν
i
and
I
ij
(See formula 1). In the case of three QoS at-
tributes (q
rt
, q
rel
, q
av
) or more simply (q
1
, q
2
, q
3
), the
2-additive Choquet Integral takes the form:
q
orch
= ν
1
q
1
+ ν
2
q
2
+ ν
3
q
3
−
1
2
I
12
|q
1
− q
2
|
−
1
2
I
13
|q
1
− q
3
| −
1
2
I
23
|q
2
− q
3
|
(3)
Once the strengths of preferences are given (e.g.,
see Table 5), a system of equations can be extracted.
Then, the parameters of the aggregation operator can
be computed by solving the system of equations. We
restrict the client to only fulfill the first diagonal of
the matrix as we consider providing all the strengths
of preferences over all the combinations of pairs of
situations is more complex and a hard task.
For example, the system of equations extracted
from Table 5 is:
q
(0,1,1)
orch
− q
(1,1,0)
orch
= h
1
.α = −ν
1
+ ν
3
− 0.5I
12
+ 0.5I
23
q
(1,1,0)
orch
− q
(0,1,0)
orch
= h
2
.α = ν
1
+ 0.5I
12
− 0.5I
13
q
(0,1,0)
orch
− q
(1,0,1)
orch
= h
3
.α = −ν
1
+ ν
2
− ν
3
q
(1,0,1)
orch
− q
(0,0,1)
orch
= h
4
.α = ν
1
− 0.5I
12
+ 0.5I
13
q
(0,0,1)
orch
− q
(1,0,0)
orch
= h
5
.α = −ν
1
+ ν
3
+ 0.5I
12
− 0.5I
23
q
(1,0,0)
orch
− q
(0,0,0)
orch
= h
6
.α = ν
1
− 0.5I
12
− 0.5I
13
ν
1
+ ν
2
+ ν
3
= 1
The system can be put in a matrix form. There-
fore, it is resolvable only and only if the matrix is
non-singular.
The client can verify if the computed weights (ν
i
)
and the interaction parameters (I
ij
) corresponds to his
preferences. This can be done by computingthe satis-
faction degrees of the binary situations and verifying
if they are conform with his preferences. Otherwise,
he can modify his strengths of preferences for best
translation of his preferences.
3.2.4 Aggregation Step
The QoS attributes values being normalized in Sec-
tion 3.2.2 and the Choquet Integral parameters being
computed in Section 3.2.3, we can now aggregate the
perceived QoS level of the services orchestration by
applying formula (3). The resulting value from the
aggregation represents the satisfaction degree of the
client from QoS point of view.
In the next section, we present a use case of the
satisfaction degree following this approach.
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS
107

Table 5: Client’s Judgements for Choquet Integral’s Parameters Determination.
(0, 1, 1) (1, 1, 0) (0, 1, 0) (1, 0, 1) (0, 0, 1) (1, 0, 0) (0, 0, 0)
(0, 1, 1) No h
1
P P P P P
(1, 1, 0) No h
2
P P P P
(0, 1, 0) No h
3
P P P
(1, 0, 1) No h
4
P P
(0, 0, 1) No h
5
P
(1, 0, 0) No h
6
4 USE CASE
E-business applications is a growing area and we can
found several e-business applications in the market re-
lating to the same business goal. We have presentedin
the previous section a B2C services orchestration al-
lowing the client to request for an insurance-car quo-
tation. Let us consider another services orchestration
satisfying the same business goal, but differs slightly.
The second services orchestration follows the model
of B2B2C applications as it involves many enterprises
(see Figure 5). These enterprises collaborate together
in order to provide to the client the best offer. Thisser-
vices orchestration is roughly the same as the already
presented above (see Figure 2) but differs when the
quotation request is accepted. In this latter case, the
quotation request is sent to two car-insurance subcon-
tractors and partners (enterprise B and C in Figure 5),
each of them establishing a quotation. Note that the
enterprises B and C do not have the same process to
establish quotations. When all quotation proposals
are received by enterprise A, they are submitted for
analyse and comparison. Then, a commercial offer
is packaged comprising the best insurance quotation
and some commercial and promotional offers as al-
ready discussed in Section 3. Finally, the commercial
offer is sent to the client.
We will now compute the satisfaction degree of
each services orchestration using the provided infor-
mations from the same client. This allows the client
to discriminate the two e-business applications and
choose the best one from his QoS point of view. Let
us consider that the client’s QoS expectations of these
e-business applications are:
S
good
= desired QoS level = (60, 1, 1)
S
neutral
= adequate QoS level = (120, 0.7, 0.6)
We will not detail the workflow pattern-based aggre-
gation phase but we give directly the perceived QoS
levels of the two services orchestration. We denote
Figure 5: B2B2C services orchestration.
the perceived QoS level of the first e-business appli-
cation (B2C) as S
1
, while the perceived QoS level of
the second e-business application (B2B2C) is denoted
as S
2
:
S
1
= (q
1
rt
, q
1
rel
, q
1
av
) = (78, 0.8, 0.95)
S
2
= (q
2
rt
, q
2
rel
, q
2
av
) = (95, 0.9, 0.9)
Given these four situations S
good
, S
neutral
, S
1
, S
2
,
the client has to compare them and express his
strengths of preferences over the difference of attrac-
tiveness between them for each QoS attribute (we
omitted details due to lack of space).
This allows us to normalize QoS attributes values
of each situation. The normalized QoS levels of situ-
ations S
1
and S
2
are as follows:
ICE-B 2011 - International Conference on e-Business
108
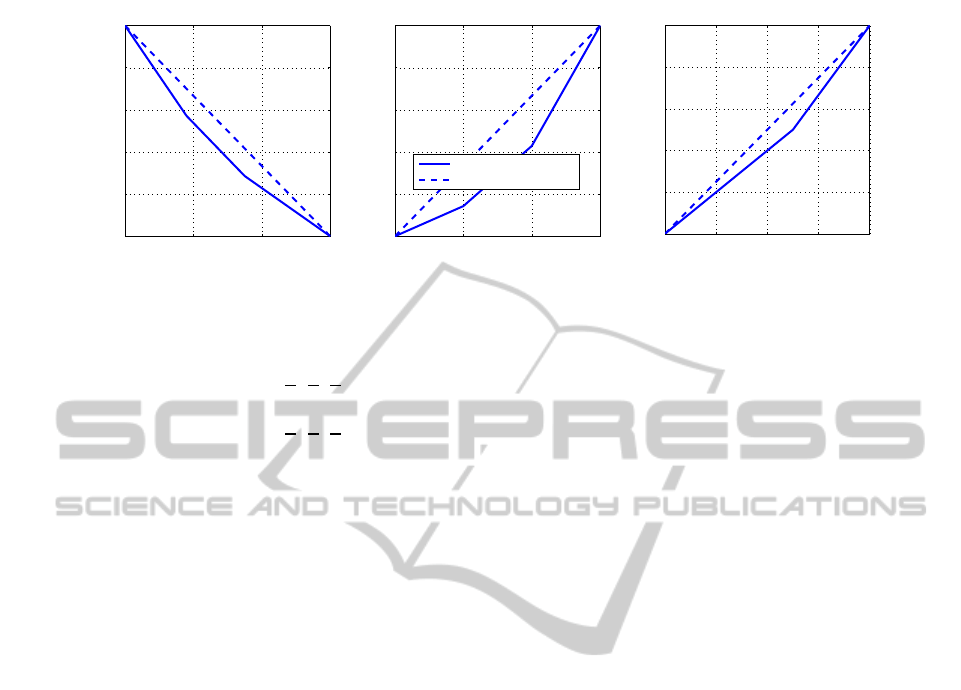
60 80 100 120
0
0.2
0.4
0.6
0.8
1
Perceived Response Time
Normalized Response Time
Response Time Normalization
0.6 0.7 0.8 0.9 1
0
0.2
0.4
0.6
0.8
1
Perceived Availability
Normalized Availability
Availability Normalization
0.7 0.8 0.9 1
0
0.2
0.4
0.6
0.8
1
Perceived Reliability
Normalized Reliability
Reliability Normalization
Consumer Informations
Linear Equations
Figure 6: QoS Attributes Normalization.
Normalized S
1
= (
4
7
,
1
7
,
1
2
)
Normalized S
2
= (
2
7
,
3
7
,
2
3
)
As we discussed above, we do not use linear equa-
tions to normalize QoS attributes but we are based
only on client’s informations (i.e., preferences and
strengths of preferences on QoS attributes). The use
of linear equations takes only into account the satis-
factory value (i.e., the best QoS attribute value) and
the unsatisfactory value (i.e., the lower QoS attribute
value) and assume that the client’s satisfaction is lin-
ear between them. This assumption is not very ac-
curate. Figure 6 shows that the client’s satisfaction
based on his provided informations can be non-linear
(curve in continuous line). We consider that this
method models the best the client’s satisfaction.
QoS attributes values being normalized, we have
to compute the parameters ν
i
and I
ij
to build the QoS
aggregation model based on the 2-additive Choquet
Integral. To this end, the client has to compare fictive
situations and expresses his strengths of preferences
on the difference of the attractiveness between them.
This leads to the following computed parameters:
ν
1
= 0.125, ν
2
= 0.55, ν
3
= 0.325
I
12
= 0.1, I
13
= 0.05, I
23
= 0.2
By applying the formula 3 at the normalized sit-
uations S
1
and S
2
, we get the following satisfactions
degree:
q
orch
(S
1
) = 0.2535, q
orch
(S
2
) = 0.4476
According to these measured satisfaction degrees, it is
clear that the client is more satisfied with the second e-
business application (B2B2C) despite the fact that its
services orchestration model contains more services.
This is explained by the fact that this client has put
much more importance at the reliability than the re-
sponse time (ν
2
> ν
1
).
5 CONCLUSIONS
This paper presents an approachthat measuresthe sat-
isfaction degree of services orchestrations related to
the client’s QoS expectations. The approach newly
combines workflow patterns aggregations rules and
the 2-additive Choquet Integral. We have shown how
does the measured satisfaction degree allow the client
to discriminate several e-business applications having
the same business goal. This permits to the client
to choose the best satisfactory e-business application
from his QoS point of view. Moreover, for one e-
business application, this approach allows us to detect
the deviation of its perceived QoS level by comparing
the measured satisfaction degree with that resulting
from the previous e-business application’s executions.
The presented approach exploits the services’ per-
ceived QoS levels that are all obtained along the exe-
cuted/runtimed services orchestration. Thus, the sat-
isfaction degree is obtained when the execution termi-
nates. Our future work aims to evaluate the satisfac-
tion degree of the services orchestration throughout
its execution and predicts the deviation of perceived
QoS level inside QoS expectations range. Whenever
we detect potential deviation, we will try to recover
it by dynamically adapting/modifyingthe services or-
chestration.
ACKNOWLEDGEMENTS
This work is partially funded by the FEDER MES
project granted by the French Rhˆone-Alpes Region.
REFERENCES
Cardoso, J., Miller, J., Sheth, A., and Arnold, J. (2002).
Modeling quality of service for workflows and web
QUALITY OF SERVICE AGGREGATION IN E-BUSINESS APPLICATIONS
109

service processes. Journal of Web Semantics, 1:281–
308.
Cliville, V., Berrah, L., and Mauris, G. (2007). Quan-
titative expression and aggregation of performance
measurements based on the macbeth multi-criteria
method. International Journal of Production Eco-
nomics, 105(1):171–189.
Coppolino, L., Romano, L., Mazzocca, N., and Salvi, S.
(2007). Web services workflow reliability estimation
through reliability patterns. Security and Privacy in
Communications Networks and the Workshops,.
Cortellessa, V. and Grassi, V. (2007). Reliability model-
ing and analysis of service-oriented architectures. In
Test and Analysis of Web Services, pages 339–362.
Springer-Verlag.
Costa, C. B., Corte, J., and Vansnick, J. (2005). On the
mathematical foundation of MACBETH. In Multiple
Criteria Decision Analysis: State of the Art Surveys,
volume 78 of International Series in Operations Re-
search & Management Science, pages 409–437.
Springer New York.
Fakhfakh, N., Verjus, H., Pourraz, F., and Moreaux, P.
(2011). Measuring the satisfaction degree of quality
attributes requirements for services orchestrations. In
in The Fourth International Conference on Commu-
nication Theory, Reliability, and Quality of Service
(CTRQ 2011), pages 89–94.
Forman, E. H. and Selly, M. A. (2001). Decision by objec-
tives: how to convince others that you are right. World
Scientific Pub Co Inc.
Gallotti, S., Ghezzi, C., Mirandola, R., and Tamburrelli,
G. (2008). Quality prediction of service composi-
tions through probabilistic model checking. In QoSA
’08: Proceedings of the 4th International Conference
on Quality of Software-Architectures, pages 119–134,
Berlin, Heidelberg. Springer-Verlag.
Grabisch, M. and Labreuche, C. (2005). Fuzzy measures
and integrals in mcda. In Multiple Criteria Decision
Analysis: State of the Art Surveys, volume 78 of Inter-
national Series in Operations Research & Man-
agement Science, pages 563–604. Springer New York.
Grabisch, M. and Labreuche, C. (2008). A decade of ap-
plication of the choquet and sugeno integrals in multi-
criteria decision aid. 4OR: A Quarterly Journal of Op-
erations Research, 6:1–44.
Herssens, C., Jureta, I. J., and Faulkner, S. (2008). Captur-
ing and using qos relationships to improve service se-
lection. In Proceedings of the 20th international con-
ference on Advanced Information Systems Engineer-
ing, CAiSE ’08, pages 312–327, Berlin, Heidelberg.
Springer-Verlag.
Jaeger, M. C., Rojec Goldmann, G., and Muhl, G. (2005).
Qos aggregation in web service compositions. In
EEE ’05: Proceedings of the 2005 IEEE International
Conference on e-Technology, e-Commerce and e-
Service (EEE’05) on e-Technology, e-Commerce and
e-Service, pages 181–185, Washington, DC, USA.
IEEE Computer Society.
Mayag, B., Grabisch, M., and Labreuche, C. (2010). A
characterization of the 2-additive choquet integral
through cardinal information. Fuzzy Sets and Systems,
In Press, Corrected Proof:–.
Menasc´e, D. A. (2003). Automatic qos control. IEEE In-
ternet Computing, 7:92–95.
Parasuraman, A., Zeithaml, V. A., and Berry, L. L. (1994).
Alternative scales for measuring service quality: A
comparative assessment based on psychometric and
diagnostic criteria. Journal of Retailing, 70(3):201 –
230.
Qi, M. and Huang, X. (2005). The design and analysis
of three-dimensional e-business model. In Proceed-
ings of the 7th international conference on Electronic
commerce, ICEC ’05, pages 136–138, New York, NY,
USA. ACM.
Rosenberg, F. (2009). QoS-Aware Composition of Adap-
tive Service-Oriented Systems. PhD thesis, Technical
University Vienna, Austria.
Sato, N. and Trivedi, K. S. (2007). Stochastic modeling
of composite web services for closed-form analysis of
their performance and reliability bottlenecks. In IC-
SOC ’07: Proceedings of the 5th international confer-
ence on Service-Oriented Computing, pages 107–118,
Berlin, Heidelberg. Springer-Verlag.
Szydlo, T. and Zielinski, K. (2008). Method of adaptive
quality control in service oriented architectures. In
Heidelberg, S. B. ., editor, Computational Science
ICCS 2008, volume 5101, pages 307–316. Springer
Berlin / Heidelberg.
van der Aalst, W., ter Hofstede, A., Kiepuszewski, B., and
Barros, A. (2003). Workflow patterns. In Distributed
and Parallel Databases, volume 14 (1), pages 5–51.
Zhong, D. and Qi, Z. (2006). A Petri net based approach for
reliability prediction of web services. In OTM Work-
shops (1), pages 116–125.
ICE-B 2011 - International Conference on e-Business
110
