
HOW TO TRANSMIT MESSAGES VIA WSN IN A HOSTILE
ENVIRONMENT
∗
Marek Klonowski, Michał Koza and Mirosław Kutyłowski
Institute of Mathematics and Computer Science, Wrocław University of Technology, Wrocław, Poland
Keywords:
Wireless sensor network, Security, Multi-hop, Message transmission, Adversary, Hostile environment.
Abstract:
In this paper we present a scheme for secure message transmission in WSN in the presence of an adversary.
We assume that the adversary can easily find some random nodes. However it is much harder for it to find
all of them (or even a concrete subset) quickly. Security of the proposed scheme is based on this practical
assumption. The protocol can be easily combined with various routing schemes as a security layer preserving
all merits of the underlying protocol for the price of reasonable communicational and storage overhead.
1 INTRODUCTION
In this paper we present and analyze a protocol for
secure messages transmission in a radio network of
weak devices. Proposed method provides confiden-
tiality of transmitted message. It can be combined
with other security methods in order to ensure au-
thentication, anonymity or other aspects of security.
It may be considered as an additional security layer.
The network we have in mind is a multi–hop sen-
sor network used for security purposes – such as a net-
work used for intrusion detection, protection of indus-
trial installations, or a military system used in a bat-
tlefield. In this type of systems it is not possible to use
very advanced general purpose security mechanisms
due to many reasons including limited computational
power, short range of communication, small memory
of devices and their cost. The nodes of the networks
can be seized by an adversary. Since the devices have
to be of low cost, we have to assume that the adver-
sary can retrieve all secret keys installed inside a cap-
tured device. On the other hand, providing security,
in particular confidentiality of processed data may be
a key-issue in many vital applications mentioned.
One of a few possible methods of improving mes-
sage confidentiality in such settings is splitting the
message into pieces. A simple solution is, for ex-
ample, to use secret sharing and send the shares via
disjoint paths. However, in this solution the adver-
sary has to capture only a single node on each path to
∗
Partially supported by Polish Ministry of Science and
Higher Education – grant No. N N206 257335
recover the message, as long as no complex methods
like onion encoding are used.
Main contribution of this paper is a secure mes-
sage transmission algorithm consisting of specific
message partitioning and routing algorithm. The solu-
tion is based on a following paradigm: the adversary
has to capture a very specific subsets of nodes in order
to break confidentiality.
1.1 Previous and Related Work
There is a long list of papers presenting solutions
based only on symmetric methods, and in particu-
lar key predistribution e.g. (REN, ; Cicho´n et al.,
2009; Du et al., 2005). The main goal of these pro-
tocols is to establish encrypted channels in the tar-
get environment between devices. The keys used are
symmetric keys shared by communicating devices.
We would like to stress that solution proposed below
can be efficiently combined with key-predistribution
scheme, including extensions like key–evolution pro-
tocols (Klonowski et al., 2007; Ren et al., 2006) pro-
viding forward or backward security. However, meth-
ods based only on key predistribution schemes does
not solve problems stated in our paper. Some other
notable security mechanisms in similar models were
presented in (Chan and Perrig, 2005; Eschenauer and
Gligor, 2002).
Proposed construction resembles in some sense
DUO-onions / Hydra-Onions described in (Iwanik
et al., 2004) (i.e. choosing several nodes in each inter-
mediate step), however goals, as well as requirements
of those protocols are completely different. There
387
Klonowski M., Koza M. and Kutyłowski M..
HOW TO TRANSMIT MESSAGES VIA WSN IN A HOSTILE ENVIRONMENT.
DOI: 10.5220/0003523403870390
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 387-390
ISBN: 978-989-8425-71-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

are also many other security protocols based on di-
viding protected content into parts – one of the most
important example is Rivest’s Chaffing and Winnow-
ing (Rivest, 1998) or (Iwanik et al., 2004). However,
to the best of our knowledge they cannot be used di-
rectly to solve issues discussed in our paper.
2 MODEL
Network Model. We consider a multi-hop radio
network. It can be seen as a communication channel
consisting of consecutive layers L
1
,... ,L
t
.
Each layer is a set of nodes. For the sake of sim-
plicity we assume that each layer contains n nodes la-
beled from 1 to n and layers are disjoint. Each pair of
nodes in consecutive layers shares a (symmetric) se-
cret key used to encrypt messages exchanged between
them. This forms a secure channel between pairs of
nodes. Thus, each node keeps 2n cryptographic keys.
Each packet broadcasted by a node from layer L
i
is received by all nodes in layer L
i+1
. Each packet
consists of a header and encrypted data. Header is
a short encrypted data that allows a node to quickly
check whether it is the proper receiver of the message.
Starting from this point, we assume that any mes-
sage sent between layers is encrypted and can be read
only by the party having access to cryptographic keys
stored in the memory of the sender or the receiver.
For the sake of clarity, this fact is not reflected in the
notation and the description of the protocol.
Note that most of assumptions can be significantly
relaxed in a straightforward manner. Indeed, pro-
posed scheme can be used not only in structured net-
works but also in a various kinds of ad hoc networks.
Model of the Adversary. The aim of the adversary
is to get the encrypted message transmitted through
the network. If the adversary is successful we say that
the message is corrupted (seized).
We assume that the adversary can capture some
subset of nodes and is able to retrieve all crypto-
graphic keys, and data from them. Moreover we as-
sume that the adversary can eavesdrop communica-
tion in the whole network.
3 PROTOCOL
We describe transmission of a message M according
to our protocol. At each layer of the network there is a
subset of l nodes (transmitting nodes) responsible for
M. The l (2 ≤ l ≤ n) is called forking parameter. It
governs security/communication trade-off – for small
l communication overhead is smaller but it is easier to
seize the message. The transmitting nodes are chosen
pseudo-randomly as described in Routing paragraph.
3.1 Protocol Overview - Single Message
The protocol uses the standard XOR-based secret
sharing procedure: in order to split a message M into
l parts: first l − 1 parts M
1
,... ,M
l−1
are chosen in-
dependently at random. The part M
l
is computed as
M
l
= M ⊗ M
1
⊗...⊗M
l−1
(⊗ denotes bitwise XOR op-
eration). It is obvious that M can be retrieved only
having all M
i
for 1 ≤ i ≤ l. Moreover, any nontrivial
subset of these parts does not reveal any information
about M.
Initialization. The source node decides to transmit
the message M (represented in the Fig. 1 as M
0
). In
the first step it partitions M
0
into l parts M
0
1
,... ,M
0
l
(the upper index denotes the layer number, the lower
index – the message part number). Then it randomly
chooses l receivers in the layer L
1
and sends each part
of the message to one of them.
The receiver of the jth part in the layer L
1
parti-
tions its part M
1
j
= M
0
j
into l parts M
1
j,1
,... ,M
1
j,l
(the
first lower index denotes part of the message, the sec-
ond - part of the part of the message) and sends them
to l nodes in the group L
2
. The receivers in L
2
are
assigned in such a way that all senders from L
1
send
their parts to the same set of l nodes from L
2
.
Message Partitioning. For i < n and j ≤ l, the jth
transmitting node in the layer L
i+1
collects l parts
M
i
1, j
,... , M
i
l, j
from l nodes from the layer L
i
and combines them to obtain M
i+1
j
:= M
i
1, j
⊗ . . . ⊗
M
i
l, j
and again splits M
i+1
j
into another l parts
M
i+1
j,1
,... , M
i+1
j,l
that are sent to the nodes in L
i+2
.
Routing. As mentioned before we want each trans-
mitting node from one layer to send parts of its mes-
sage to exactly the same l nodes from the following
layer. As shown in Fig. 1 each packet exchanged be-
tween layers contains not only a message part but also
a pseudo random number r generated by its sender.
Each receiver combines all received random numbers
and basing on the result deterministically selects l
transmitting nodes in the following layer. Then it gen-
erates its own pseudo random number and attaches it
to each packet it sends to the receivers in the next
layer. This way all l receivers get the same set of
pseudo random values and can independently deter-
mine the same set of l receivers in the following layer.
SECRYPT 2011 - International Conference on Security and Cryptography
388

Sink. From the last layer all parts are sent to a
sink representing the receiver of the original message.
Note that: M
i
1, j
⊗ ... ⊗ M
i
l, j
= M
i+1
j
= M
i+1
j,1
⊗ ... ⊗ M
i+1
j,l
Message parts are repartitioned on each level so that
it is not possible to reconstruct the original message
capturing some parts on each layer – all parts from at
least one layer is necessary.
The idea of the protocol is described in Fig. 1.
M
0
M
1
1
M
1
2
M
1
3
M
1
1,1
, r
1
1
M
1
1,2
, r
1
1
M
1
1,3
, r
1
1
M
1
2,1
, r
1
2
M
1
2,2
, r
1
2
M
1
2,3
, r
1
2
M
1
3,1
, r
1
3
M
1
3,2
, r
1
3
M
1
3,3
, r
1
3
M
2
1
M
2
2
M
2
3
M
2
1,1
, r
2
1
M
2
1,2
, r
2
1
M
2
1,3
, r
2
1
M
2
2,1
, r
2
2
M
2
2,2
, r
2
2
M
2
2,3
, r
2
2
M
2
3,1
, r
2
3
M
2
3,2
, r
2
3
M
2
3,3
, r
2
3
M
0
1
, r
0
M
0
2
, r
0
M
0
3
, r
0
M
3
1
M
3
2
M
3
3
Figure 1: Exemplary protocol execution for one message
and l = 3.
Note that this protocol may be used with various
other methods - for example with Message Authenti-
cation Codes (MAC) to make the change of the mes-
sage more difficult or secret sharing scheme (Shamir,
1979) for robustness.
4 SECURITY ANALYSIS
In this section we discuss security aspects of the pro-
posed scheme in some realistic scenarios. We assume
that adversary can capture at most K nodes. Our anal-
ysis is based on the following observations:
1. The adversary is able to learn the plaintext, if he
controls all transmitting nodes for this plaintext in at
least one layer.
2. Information gained by the adversary from nodes
in one layer does not help to corrupt the message by
attacking another layer.
Since our protocol is based on one-time-pad en-
coding offering unconditional security, the analysis
boils down in fact to combinatorial questions.
First, we discuss the case, wherein a single mes-
sage is transmitted through the channel.
Nonadaptive Attack. In this subsection we con-
sider a scenario, wherein the adversary chooses the
nodes to be corrupted before the transmission. Let
us assume that the adversary knows the partition into
n-node layers and corrupts arbitrary k
i
nodes in the
ith layer (provided that
∑
i
k
i
≤ K). First note that if
k
i
< l the adversary does not learn anything from the
ith layer. On the other extreme, if k
i
= n for at least
one layer, the adversary breaks each message for sure.
Thus, the interesting case is that n > K ≥ l.
Below we investigate, which strategy of assign-
ing the numbers k
1
,k
2
,... ,k
t
maximizes adversary’s
chances of corrupting the message (equivalently, at
some layer all l nodes transmitting a message are un-
der adversary’s control). Let p
l,n
(k
1
,k
2
,... ,k
t
) be the
probability that the adversary will corrupt the mes-
sage provided that he controls k
i
nodes in the ith layer.
It can be proved that the function p
l,n
is maximized if
the value k
1
is maximized. I.e the adversary chooses
all K nodes from a single layer. More precisely one
can prove following theorem
Theorem 4.1. Let n > K ≥ l be the number of cor-
rupted nodes and k
i
be the number of corrupted nodes
in the ith layer for i = 1,... ,t. The strategy of putting
all corrupted nodes in exactly one layer maximizes
probability of the adversary for corrupting the mes-
sage.
The above theorem is intuitive, hovever the the
formal proof is non-trivial.
By Theorem 4.1 we get immediately the following
corollary:
Corollary 4.1. In the system with splitting parameter
l, with n nodes in each layer, and the adversary ca-
pable to corrupt K nodes, the probability that the ad-
versary corrupts a transmitted message is 0 if K < l,
K
l
/
n
l
if l ≤ K < n, and 1if K ≥ n.
Random Choice of Captured Nodes. Now we as-
sume that an adversary has access to exactly K nodes
randomly chosen out of all L = n · t nodes. We be-
lieve that such a model is very realistic for most of
ad hoc wireless sensor networks. Indeed, collecting
small devices distributed over a large area in restricted
time significantly reduces possibility of collecting de-
vices that belongs to a particular layer.
Lemma 4.1. Let us assume that an adversary has ac-
cess to K nodes chosen at random out of L = n · t
nodes in total. Let us assume that a single message is
transmitted through the network with splitting param-
eter l. Then the probability that the adversary collects
all l transmitting node from at least one layer is
S
n
=
t
∑
i=1
(−1)
i+1
t
i
(K
il
)
+
L
il
< .
1
2
1+
1
t
l
t
−
1−
1
t
l
t
.
In the last inequality we assumed without signifi-
cant limitation of generality that t is an odd number.
Standard proof is skipped. Fig. 2 shows obtained es-
timations for small number of captured nodes.
Nodes Chosen After the Transmission. Let us
consider a scenario wherein the adversary can ob-
serve the traffic, localize transmitting devices and, af-
ter transmission, capture K devices. Obviously, as
long as K < l it is not able to corrupt any message.
HOW TO TRANSMIT MESSAGES VIA WSN IN A HOSTILE ENVIRONMENT
389
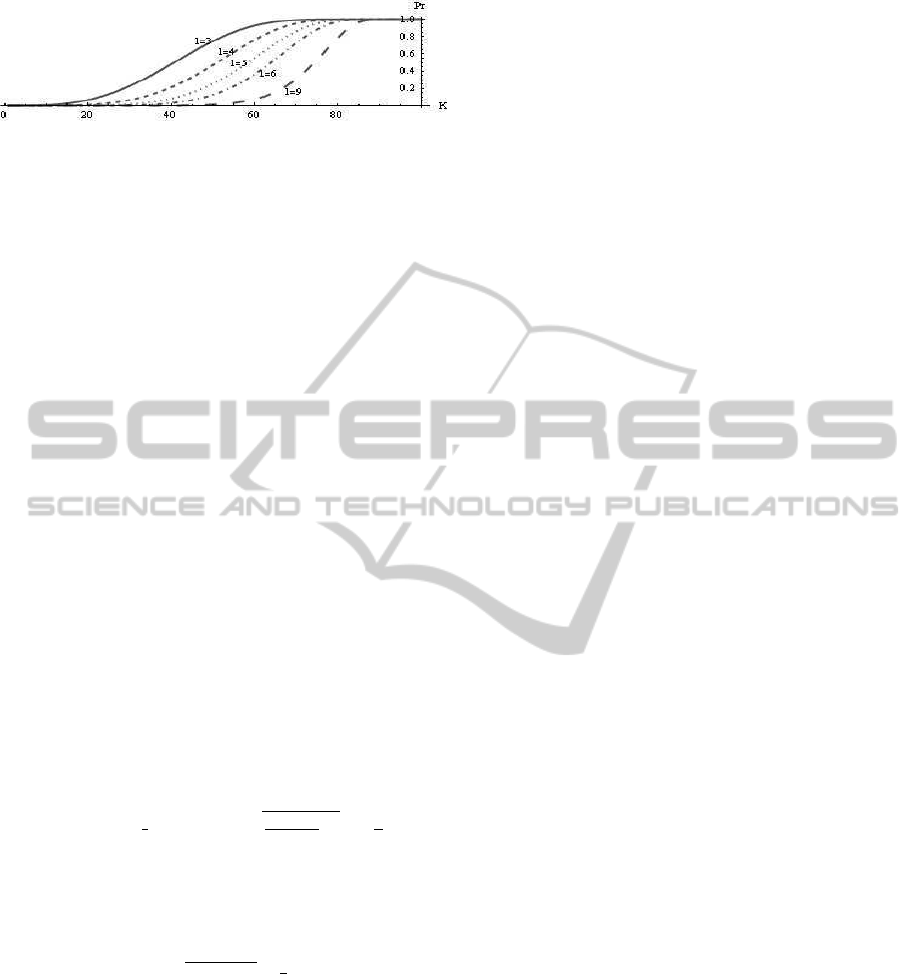
Figure 2: A bound on probability that an adversary col-
lects all l parts from one layer for L = 100, t = 10, and
l = 3,4,5, 6,9 respectively for t · l < K < L/t.
Otherwise, in the case of a single transmitted mes-
sage, the strategy of the adversary is trivial - it chooses
l transmitting nodes from any layer.
The situation is much more complicated when the
adversary can observe simultaneous transmission of
many, say N messages and then capture some nodes.
The number of message pieces transmitted through
different nodes is not the same. The adversary may
increase his chances by choosing the nodes with rela-
tively many transmissions going through.
Since it is optimal to attack one layer, we consider
a single layer. To corrupt one of N messages the ad-
versary must collect all l pieces of this message. As-
sume that the adversary is able to corrupt K nodes.
Let S
K
be a family of all subsets of all n nodes of car-
dinality K. If subset S ∈ S
K
contains all transmitting
nodes of exactly x messages, we say that x messages
go through S. Let MAX
n,K
be a random variable de-
noting the number of messages corrupted by the ad-
versary if he controls K out of n nodes chosen in the
optimal way. Of course, the adversary does not know
the optimal subset of nodes to attack, but we wish to
check what would be adversary’s advantage with this
knowledge granted for free.
Theorem 4.2.
Pr
"
MAX
n,K
≥ Np +
1
3
log
n
K
N
1+
s
18Np
log
n
K
N
+ 1
!#
≤
1
N
.
In particular, for realistic settings and large (com-
pared to the number of devices) number N of sent
messages we get the following bound:
Corollary 4.2. For log
n
K
N
< N p following relation
holds: Pr
h
MAX
n,K
≥ N p+ 1.5
q
N log
n
K
N
p
i
≤
1
N
.
Proof. Due to space limitations we skip proofs.
Practical meaning of this bound is that the advan-
tage of the adversary given the possibility to choose
nodes after transmission is not significantly greater
than if the adversary would choose nodes at ran-
dom. Indeed, in general for fixed n,K,l we have
MAX
n,K
= N · p+ o(N) w.h.p.
5 CONCLUSIONS
The main proposal of this paper is to couple security
mechanisms for security related application of sen-
sor networks (or just networks with confidential in-
formation) with mechanisms that are based on phys-
ical difficulty to find devices located at random. We
believe that from practical point of view this is a cru-
cial mechanism and it can/should be exploited when
constructing communication protocols in some spe-
cific networks (like military networks). The protocol
presented is just an example of such an approach.
REFERENCES
Chan, H. and Perrig, A. (2005). Pike: Peer intermediaries
for key establishment in sensor networks. In The 24th
Conference of the IEEE Communications Society (In-
focom 2005).
Cicho´n, J., Grza´slewicz, J., and Kutyłowski, M. (2009).
Key levels and securing key predistribution against
node captures. In Dolev, S., editor, ALGOSENSORS,
volume 5804 of Lecture Notes in Computer Science,
pages 64–75. Springer.
Du, W., Deng, J., Han, Y. S., Varshney, P. K., Katz, J.,
and Khalili, A. (2005). A pairwise key predistribution
scheme for wireless sensor networks. ACM Trans. Inf.
Syst. Secur., 8(2):228–258.
Eschenauer, L. and Gligor, V. D. (2002). A key-
management scheme for distributed sensor networks.
In CCS ’02: Proceedings of the 9th ACM conference
on Computer and communications security, pages 41–
47, New York, NY, USA. ACM Press.
Iwanik, J., Klonowski, M., and Kutyłowski, M. (2004).
Duo–onions and hydra–onions – failure and adver-
sary resistant onion protocols. In Proceedings of
the IFIP TC-6 TC-11 Conference on Communica-
tions and Multimedia Security 2004. Springer Boston,
Springer Boston.
Klonowski, M., Kutyłowski, M., Ren, M., and Rybarczyk,
K. (2007). Forward-secure key evolution in wireless
sensor networks. In Bao, F., Ling, S., Okamoto, T.,
Wang, H., and Xing, C., editors, CANS, volume 4856
of Lecture Notes in Computer Science, pages 102–
120. Springer.
Ren, M., Das, T. K., and Zhou, J. (2006). Diverging keys in
wireless sensor networks. In Katsikas, S. K., Lopez,
J., Backes, M., Gritzalis, S., and Preneel, B., editors,
ISC, volume 4176 of Lecture Notes in Computer Sci-
ence, pages 257–269. Springer.
Rivest, R. (1998). Chaffing and winnowing: Confidentiality
without encryption.
Shamir, A. (1979). How to share a secret. Commun. ACM,
22(11):612–613.
SECRYPT 2011 - International Conference on Security and Cryptography
390
