A GENETIC APPROACH FOR IMPROVING THE SIDE

INFORMATION IN WYNER-ZIV VIDEO CODING WITH

LONG DURATION GOP

Charles Yaacoub, Joumana Farah and Chadi Jabroun

Faculty of Engineering, Holy-Spirit University of Kaslik, Jounieh, Lebanon

Keywords: Distributed video coding, Frame interpolation, Genetic algorithms, Side information, Wyner-Ziv coding.

Abstract: This work tackles the problem of side information generation for the case of large-duration GOPs in

distributed video coding. Based on a previously developed technique for side-information enhancement, we

develop a genetic algorithm particularly designed for large GOPs, taking into account the GOP size, the

additional bitrate incurred by encoding hash information, as well as the decoding complexity. The proposed

algorithm makes use of different interpolation methods available in the literature in a fusion-based

approach. A significant gain in the average PSNR that can reach 2 dB is observed with respect to the best

performing interpolation technique, while the algorithm is run for no more than 18% of the total number of

blocks in a given video sequence. On the other hand, while the encoding complexity is a main concern in

distributed video coding, the proposed solution incurs no additional complexity at the encoder side in the

case of hash-based Wyner-Ziv video coding.

1 INTRODUCTION

Distributed video coding (DVC), or Wyner-Ziv

(WZ) video coding (Aaron et al, 2002), is a video

compression technique that has occupied the interest

of the research community for the last decade. Based

on the Slepian-Wolf theorem (Slepian, Wolf, 1973)

for distributed source compression that was later

extended by Wyner and Ziv (Wyner, Ziv, 1976) for

the case of lossy source coding, DVC consists of

first compressing a subset of frames, called Key

frames, using traditional intra-coding techniques.

One or more frames following each key frame,

called WZ frames, are then compressed by

appropriate puncturing of the parity bits at the output

of a channel coder. At the receiver side, previously

decoded (key or WZ) frames are used to interpolate

the necessary side information (SI) for the decoding

process. The interpolated SI is fed to the channel

decoder as a noisy version of the missing WZ frame,

where the received parity bits are used to correct

estimation errors and reconstruct the output video.

Different techniques for generating accurate side

information have been presented in the literature.

Aaron et al. first proposed average interpolation and

motion-compensated interpolation in (Aaron et al,

2002). In (Ascenso et al., 2005), Ascenso et al.

presented an improved motion-compensated

interpolation using spatial motion smoothing. In

hash-based DVC (Aaron et al., 2004, Ascenso et al.,

2007), hash bits were used to improve the quality of

the side information. Multiple hypothesis techniques

were developed in (Misra et al., 2005) and (Kubasov

et al., 2007), where two different frames were used

as side information for the decoding of a single WZ

frame. Each of these methods outperforms some of

the others in particular situations (e.g. background

motion, moving objects, etc…).

In (Yaacoub et al., 2009b and 2009c, and

Yaacoub, 2009), Yaacoub et al. developed a novel

genetic-based frame-fusion algorithm that relies on

previously developed interpolation techniques to

select the best SI candidate for each region within a

frame. Preliminary results showed that the proposed

genetic algorithm (GA) offers exceptional

performance in complex motion scenes. However,

the rate cost due to sending hash information was

not taken into consideration, complexity issues were

not considered, and the size of a Group of Pictures

(GOP) was limited to 2. In (Maugey et al., 2010),

authors tackle the problems of complexity and hash

rate reduction by selectively running the fusion

algorithm, only for the blocks where known

interpolation techniques fail to yield a good

estimation. In this paper, in contrast with the work in

Yaacoub C., Farah J. and Jabroun C..

A GENETIC APPROACH FOR IMPROVING THE SIDE INFORMATION IN WYNER-ZIV VIDEO CODING WITH LONG DURATION GOP.

DOI: 10.5220/0003526300970103

In Proceedings of the International Conference on Signal Processing and Multimedia Applications (SIGMAP-2011), pages 97-103

ISBN: 978-989-8425-72-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(Maugey et al., 2010) where the GOP size if fixed to

2, and the amount of hash information is constant

throughout the sequence (fixed number of hash

words and fixed quantization matrix), the bitrate

associated with hash information is adaptively

varied according to the GOP size and the quality of

the available side information. If high-quality SI is

obtained without the need for hash bits, no hash

information is sent. Otherwise, the system

dynamically determines the need for either running

the genetic-based fusion algorithm, or simply relying

on the received hash words to optimize the SI

quality without running the GA, thus further

reducing the decoding complexity.

The remainder of this paper is organized as

follows. In Section 2, the initially proposed GA-

based frame fusion algorithm is briefly reviewed and

modifications are proposed to take into account

different GOP sizes. In Section 3, an improved

algorithm is proposed taking into account the

quantization of hash information, the additional

complexity incurred at the decoder, and the

increased GOP size. Simulation results are shown

and discussed in Section 4 and finally, conclusions

are drawn in Section 5.

2 REVIEW OF GA-BASED

FRAME FUSION

Based on the principles of evolution and natural

genetics, Genetic Algorithms (GAs) (Goldberg,

1989) are well suited for optimization problems. In

this paper, the use of a GA in a fusion-based

approach aims at improving the quality of the side

information relying on several initial estimations. In

the following, the GA will be briefly reviewed for

clarity.

The GA operates at the block level. Initially, for

a given block in the WZ frame, each of the co-

located blocks in the available SI candidate frames

represents a possible solution (referred to as a

chromosome) which consists of a set of pixels

(genes). A population is a set of chromosomes in the

solution space. The similarity between a given

chromosome and the corresponding block in the WZ

frame represents its fitness, evaluated as the inverse

of the mean-square-error (MSE) between a received

hash word and a local hash word extracted from the

candidate block.

An initial population is first generated by

duplicating each candidate block a number of times

proportional to its fitness, until the desired

population size is reached. The chromosomes are

then randomly shuffled and arranged into pairs.

Each pair (parent chromosomes) undergoes a

vertical crossover followed by a horizontal crossover

(Yaacoub et al., 2009b and 2009c, and Yaacoub,

2009) to yield a couple of child chromosomes

(called offsprings). In order to extend the solution

space and reduce the possibility of falling into local

optima, a mutation is performed on offsprings by

randomly selecting a gene and inverting one of its

bits. The fitness of the resulting chromosomes is

then evaluated and a subset of the fittest

chromosomes is selected, while the others are

deleted to make room for new ones. The surviving

chromosomes are then duplicated a number of times

proportional to their fitness and the whole procedure

is repeated until the maximum allowed number of

iterations is reached. Finally, the fittest chromosome

is selected and its fitness compared to a threshold

. This allows determining whether the GA

converged enough to yield improved side

information or not. In the former case, the GA

output is considered as the best candidate block to be

used as side information for decoding the co-located

block in the WZ frame. In the latter case, simply

computing the inverse DCT of the received hash

word often yields a better result.

This algorithm was first developed in (Yaacoub

et al., 2009b and 2009c, and Yaacoub, 2009) and

evaluated for GOPs of size 2. In the following, we

consider the same algorithm for larger GOPs. In this

case, the order of WZ-frame decoding within a GOP

is the same as in (Yaacoub et al., 2009a). GA is

initialized with the nearest previously decoded WZ

frame (within the same GOP) if it exists, the key

frames of the current GOP, and the different

interpolated frames obtained by Average

Interpolation (AVI) (Aaron et al., 2002), Motion

Compensated Interpolation (MCI) (Aaron et al.,

2002), and hash-based MCI (HMCI) (Aaron et al.,

2004). It is essential at this point to mention that any

existing interpolation technique can be used for

initializing the GA; having a diversity of candidates

extends the solution space of the algorithm.

Therefore, advanced techniques such as in (Ascenco

et al., 2005) can be used to improve the output

quality. However, in this study, we limit our

initialization phase to the three simple interpolations

mentioned earlier.

As an example, let us consider a GOP of size 4

consisting of a key frame F

and WZ frames F

, F

and F

. Denote F

the key frame of the next GOP.

Starting from WZ frame F

, its initial candidates are

, F

, AVI(F

), MCI(F

), and HMCI(F

For WZ frame F

, the initial candidates are F

, F

the reconstructed version of F

), AVI(F

AVI(F

), MCI(F

), HMCI(F

)

SIGMAP 2011 - International Conference on Signal Processing and Multimedia Applications

and HMCI(F

). Finally, for WZ frame F

, frames

used as initial candidates are F

, F

, AVI (F

AVI(F

), MCI(F

), HMCI(F

)

and HMCI(F

In Figure 1, we show the result of running the

algorithm with GOP sizes going from 2 to 5, for

Carphone and News QCIF video sequences. The

curves shown present the average PSNR of the side

information obtained with AVI, MCI, HMCI, the

GA, and inverse DCT of received hash (IDCT). The

IDCT PSNR in News sequence is nearly constant at

28 dB, but the figure has been cropped for clarity. It

can be observed that, as expected, the quality of the

side information is degraded when the GOP size

increases. The gap in PSNR between the GA and the

hash-based motion-compensated interpolation

(HMCI) increases from 1.3 dB to 2.7 dB in

Carphone, and from 2 dB to 2.5 dB in News. Not

only the best performance is always obtained with

GA, but the GA also shows the best robustness

against the increase in GOP size.

These preliminary results motivate further research

in optimizing GA-based fusion for WZ video coding

with GOP sizes greater than 2. For this reason, in the

following, an enhanced GA-based fusion algorithm

will be presented, taking into account decoding

complexity, rate control, and non-perfectly

recovered hash information.

3 ENHANCED GA-BASED

FUSION ALGORITHM

In (Yaacoub et al., 2009b), authors construct the

hash word for a given macroblock (16 x 16 pixel

)

using a subset of DCT coefficients having the

highest energy levels. In practice, this requires

transmitting a binary map indicating the positions of

the transmitted coefficients in order for the decoder

to be able to decode the received data. As a result, in

addition to the bitrate required for the transmission

of hash DCT coefficients, a rate excess is required to

transmit the binary map. After intensive simulations

and tests, we have noticed that when the DCT

coefficients are quantized, increasing the number of

coefficients in a hash word allows to overcome the

performance degradation due to sending quantized

DCT coefficients at fixed positions (instead of

choosing those with the highest energy levels), at a

rate cost better than encoding a binary map.

A flowchart diagram of the proposed fusion

technique is shown in Figure 2. At the decoder side,

for each macroblock in the current WZ frame,

motion estimation is first performed in order to

interpolate the corresponding side information

Figure 1: Side information PSNR for Carphone (left) and

News (right).

(MCI). At this point, the decoder determines the

motion level (estimated by the MSE) between the

blocks involved in the interpolation process as in

(Maugey et al., 2010). If the MSE does not exceed a

threshold T

, the system assumes that MCI would

yield a high-quality SI and therefore, there is no

need to transmit additional hash information and

perform other interpolation techniques. In the other

case, MCI is assumed to fail and the decoder

requests a hash word from the encoder.

On the other hand, we know that in some

situations (e.g. high motion), the interpolation

techniques (whether hash-based or non-hash-based)

used to initialize the GA often fail, which also

degrades the performance of the GA. In this case,

simply computing the IDCT using the received hash

word (by first substituting the missing coefficients

with zeros) often yields a better result, provided that

a sufficient number of coefficients was transmitted.

Therefore, in contrast with (Maugey et al., 2010), if

the motion level (i.e. the MSE between the forward

and backward motion-estimated macroblocks)

exceeds a threshold T

> T

, no interpolation is

performed and the IDCT macroblock is taken as side

information. If neither MCI nor IDCT were selected

as side information, a fusion of different

interpolation techniques is assumed to yield a better

SI and the genetic-based fusion algorithm presented

in Section 3 is run. As explained in the previous

section, the fitness of the GA output is finally

compared to a threshold T

in order to determine

whether the GA converged to a better SI and select

the GA-generated output as side information, or

otherwise, select the IDCT.

A GENETIC APPROACH FOR IMPROVING THE SIDE INFORMATION IN WYNER-ZIV VIDEO CODING WITH

LONG DURATION GOP

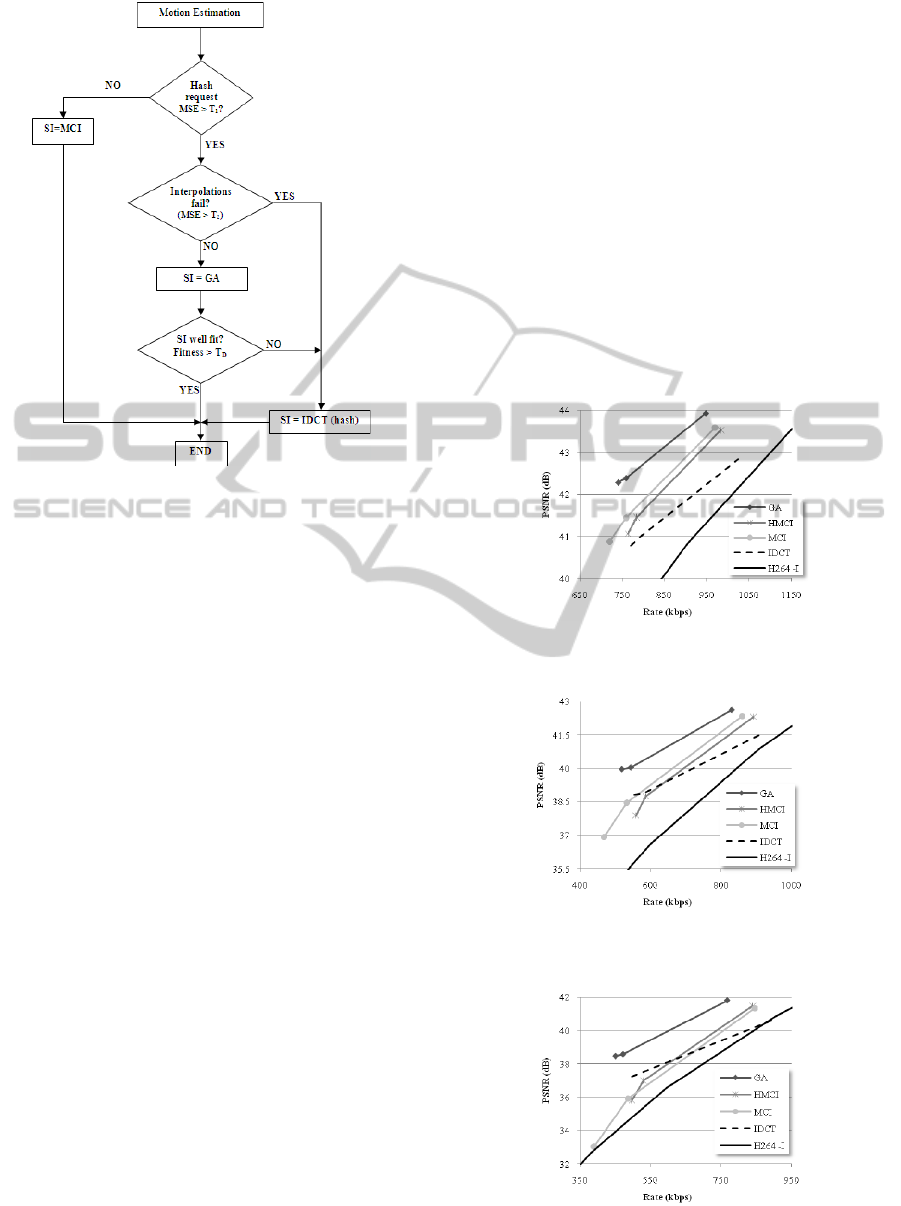
Figure 2: Flowchart diagram of the enhanced genetic-

based fusion algorithm.

4 EXPERIMENTAL RESULTS

The Wyner-Ziv video codec and the GA parameters

used in our simulations are the same as in (Yaacoub

et al., 2009b), with the exception that the side

information is generated as described in Sections 2

and 3. We consider different QCIF video sequences

encoded at a rate of 30 frames per second (fps) and

the key frames are encoded using baseline H.264

Intra coding (ITU-T, 2003).

Macroblocks (16x16) are considered in this

study, which allows reducing the number of times

the GA is run compared to 4x4 blocks, and thus

reduce the overall decoding complexity. Besides,

quantization matrices were designed taking into

account the block dimensions and the GOP size, as

well as the following constraints:

- The number of DCT coefficients in a hash word

must be large enough in order for the fitness

function to provide accurate information about

the quality of the candidate blocks.

- The amount of hash information transmitted for

the generation of SI frames belonging to long-

duration GOPs must be varied according to their

position within the GOP.

- The rate required for the coding of hash words

must not be too large in order for the rate cost

not to overcome the gain in PSNR. This allows

the overall RD performance to be improved.

- The rate assigned for low-frequency coefficients

should obviously be greater than the one

assigned for high-frequency coefficients.

Further quantization matrix design details are not

presented in this paper due to space limitations.

Thresholds T

, T

, and T

are varied to adapt to the

quantization matrix.

Figures 3 to 6 show the RD curves for News

sequence with GOP sizes 2, 4, 6 and 8, respectively.

The performance of the WZ codec with GA-based

fusion is compared with the cases where either MCI,

HMCI, or IDCT is used as side information. It can

be observed that the gain in PSNR obtained by using

HMCI with respect to MCI is compensated by a

greater rate cost that degrades the overall RD

performance for GOPs of size 2 and 4. Additionally,

simply using the IDCT may yield a better

performance compared to MCI and HMCI if the

Figure 3: RD curves for News sequence with a GOP size =

Figure 4: RD curves for News sequence with a GOP size =

Figure 5: RD curves for News sequence with a GOP size =

SIGMAP 2011 - International Conference on Signal Processing and Multimedia Applications

100

Figure 6: RD curves for News sequence with a GOP size =

proposed fusion algorithm is not run. However, for

larger GOPs, HMCI yields slightly better

performance than MCI, and IDCT yields the worst

performance at high bitrates.

The proposed technique for generating the side

information allows the system not only to converge

towards the best performing SI generation but rather

to improve the overall performance compared to the

best case among non GA-based techniques. For

example, without fusion, the best performing SI is

either MCI or HMCI at high bitrates, and IDCT for

large GOPs at low bitrates. In the former case, the

gain obtained with the GA with respect to either

MCI or HMCI reaches 2 dB. In the latter case, the

gain reaches 1.5 dB with respect to IDCT. Besides,

for the News video sequence, the GA-based codec

always outperforms a standard H.264-Intra codec,

where the gain in average PSNR can reach 4.5 dB.

Figures 7 to 10 show the RD curves for Trevor

with GOP sizes of 2, 4, 6 and 8, respectively. It can

be noticed that for a GOP of size 6, the GA gain

obtained with respect to IDCT can reach 1 dB at low

rates. As for the smaller GOPs, the GA outperforms

MCI by 0.8 dB (GOP size = 4) and 0.3 dB (GOP

size = 2) at low rates, whereas both RD curves (GA

and MCI) nearly overlap at high rates. This is due to

the fact that the proposed adaptive algorithm

determined that most of the time, the MCI would

yield the best result and therefore, it was often

chosen as the final SI. On the other hand, it can be

noticed that with Trevor, the H.264-Intra codec

outperforms the WZ codec, regardless of the SI

generation method used. This is due to the particular

nature of this video. In fact, in the first part of the

sequence, we can observe six different sub-windows

each showing a different play with different motion

levels, whereas in the second part, one play occupies

the whole screen. Having a sudden scene change

with completely different content creates a burst of

WZ frames with very low PSNR, which

significantly reduces the average PSNR of the

sequence. As the GOP size increases, the burst

length (i.e. the number of WZ frames) with

erroneous content increases, which yields a greater

performance degradation as it can be noticed in

figures 7 to 10. However, the GA-based fusion

reduces the performance GAP between WZ and

H.264-Intra codecs to a large extent.

Similar results were observed with different

video sequences. An estimation of the computational

load incurred by running the initial GA (Section 2)

can be found in (Yaacoub, 2009), where the GA was

run for every block within a WZ frame. With the

enhanced GA (Section 3), we observed that the

percentage of blocks where the GA was run is 4%

with Trevor and 6% with news, when the GOP size

is 2. These percentages become 5% and 6.5% for

Trevor and News, respectively, when the GOP size

is 4. For larger GOPs, GA was run for no more than

18% of the blocks. Consequently, the overall

complexity is reduced to a large extent, compared to

the initial GA-based fusion.

Figure 7: RD curves for Trevor sequence with a GOP size

= 2.

Figure 8: RD curves for Trevor sequence with a GOP size

= 4.

Figure 9: RD curves for Trevor sequence with a GOP size

= 6.

A GENETIC APPROACH FOR IMPROVING THE SIDE INFORMATION IN WYNER-ZIV VIDEO CODING WITH

LONG DURATION GOP

101

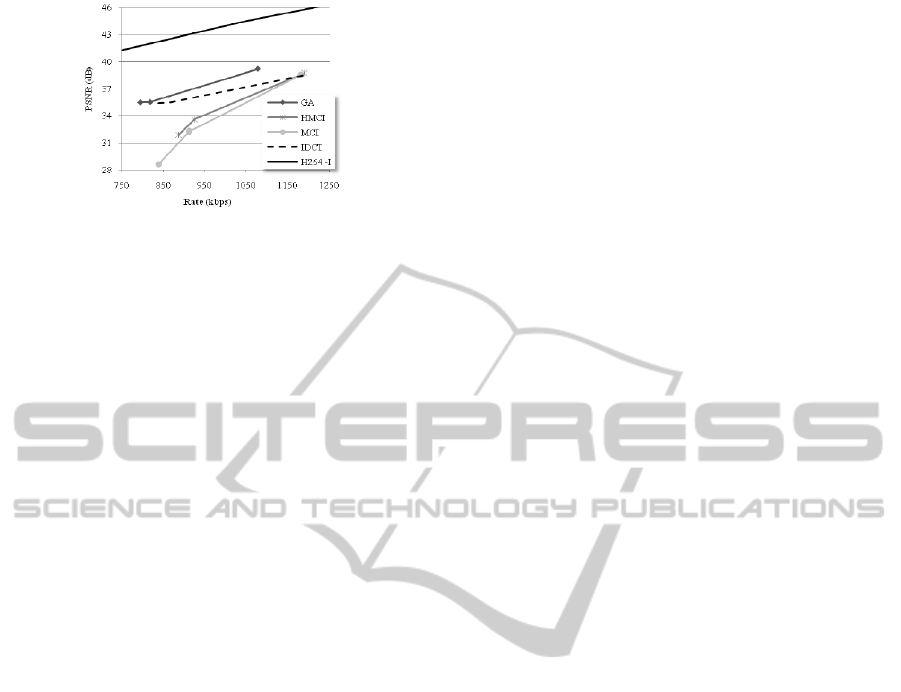
Figure 10: RD curves for Trevor sequence with a GOP

size = 8.

5 CONCLUSIONS

This paper presents an enhanced genetic algorithm

for improving the side information in Wyner-Ziv

video coding with large GOP size. The algorithm

makes use of the different interpolation techniques

available in the literature in a fusion-based approach

in order to improve the overall RD performance.

Particularly designed for long-duration GOPs, the

proposed algorithm also takes into consideration the

rate cost needed to encode hash information as well

as the additional complexity incurred at the decoder.

Simulation results show that a PSNR gain of 2

dB can be reached with the proposed fusion

algorithm without any additional complexity at the

encoder side. In our future work, GA-based fusion

will be considered in the context of multiview DVC,

where multiple views can provide crucial

information for initializing the GA. Additionally,

methods for reducing the overall complexity as well

as optimizing the quantization matrices will be

developed, with the aim of further improving the RD

performance, particularly for large GOPs.

ACKNOWLEDGEMENTS

This work was partly supported by a research grant

from the Franco-Lebanese CEDRE program.

REFERENCES

Aaron A., Rane S., Girod B., 2004. Wyner-Ziv video co-

ding with hash-based motion compensation at the

receiver. In IEEE International Conference on Image

Processing, Singapore.

Aaron A., Zhang R., Girod B., 2002. Wyner-Ziv Coding

of Motion Video. In 36th Asilomar Conf. Signals,

Systems and Computers, pp. 240-244.

Ascenso J., Brites C., Pereira F., 2005. Improving frame

interpolation with spatial motion smoothing for pixel

domain distributed video coding. In 5th EURASIP

Conference on Speech and Image Processing,

Multimedia Communications and Services, Smolenice,

Slovak Republic.

Ascenso J., Pereira F., 2007. Adaptive hash-based side

information exploitation for efficient Wyner-Ziv video

coding. In International Conference on Image

Processing, USA.

Chang P. H., Leou J. J., Hsieh H. C., 2001. A genetic al-

gorithm approach to image sequence interpolation. In

EURASIP Journal on Signal Processing: Image

Communication, Vol. 16, No. 6, pp. 507-520.

Goldberg D. E., 1989. Genetic Algorithms: Search, Opti-

mization, and Machine Learning, Addison-Wesley,

Reading, MA.

Hung-Kei Chow K., Liou M. L., 1993. Genetic motion

search algorithm for video compression. In IEEE

Trans. Circuits and Systems for Video Technology,

Vol. 3, pp. 440-445.

ITU-T and ISO/IEC JTC1, 2003. Advanced Video Coding

for Generic Audiovisual Services. ITU-T Recommen-

dation H.264 – ISO/IEC 14496-10 AVC.

Kubasov D., Nayak J., Guillemot C., 2007. Optimal

Reconstruction in Wyner-Ziv Video Coding with

Multiple Side Information. In 2007 IEEE International

Workshop on Multimedia Signal Processing, Chania,

Crete, Greece.

Lin C-H., Wu J-L., 1996. Genetic block matching

algorithm for video coding. In IEEE International

Conference on Multimedia Computing and Systems,

Japan.

Maugey T., Yaacoub C., Farah J., Cagnazzo M., Pesquet-

Popescu B., 2010. Side information enhancement

using an adaptive hash-based genetic algorithm in a

Wyner-Ziv context. In 2010 IEEE International

Workshop on Multimedia Signal Processing, Saint-

Malo, France.

Misra K., Karande S., Radha H., 2005. Multi-hypothesis

distributed video coding using LDPC codes. In 43rd

Annual Allerton Conference on Communication,

Control, And Computing, Monticello, USA.

Slepian D., Wolf J. K., 1973. Noiseless Coding of

Correlated Information Sources. In IEEE Trans.

Information Theory, Vol. IT-19, pp. 471-480.

Wyner A., Ziv J., 1976. The Rate-Distortion Function for

Source Coding with Side Information at the Decoder.

In IEEE Trans. Information Theory, Vol. IT-22, pp. 1-

10.

Yaacoub C., 2009. Joint source-channel coding for the

optimization of the distributed coding of video sources

transmitted over wireless channels. PhD Thesis,

Telecom ParisTech.

Yaacoub C., Farah J., Pesquet-Popescu B., 2008.

Feedback Channel Suppression in Distributed Video

Coding with Adaptive Rate Allocation and Quanti-

zation for Multiuser Applications. In EURASIP

Journal on Wireless Communications and Networking.

Yaacoub C., Farah J., Pesquet-Popescu B., 2009a. New

Adaptive Algorithms for GOP Size Control with

Return Channel Suppression in Wyner-Ziv Video

SIGMAP 2011 - International Conference on Signal Processing and Multimedia Applications

102

Coding. In International Journal of Digital

Multimedia Broadcasting, special issue on Advances

in Video Coding for Broadcast Applications.

Yaacoub C., Farah J., Pesquet-Popescu B., 2009b. A

Genetic Algorithm for Side Information Enhancement

in Distributed Video Coding. In IEEE International

Conference on Image Processing, Cairo, Egypt.

Yaacoub C., Farah J., Pesquet-Popescu B., 2009c.

Improving Hash-Based Wyner-Ziv Video Coding

Using Genetic Algorithms. In 5th International Mobile

Multimedia Communications Conference, London,

UK.

A GENETIC APPROACH FOR IMPROVING THE SIDE INFORMATION IN WYNER-ZIV VIDEO CODING WITH

LONG DURATION GOP

103