
TEST GENERATION FROM BOUNDED ALGEBRAIC
SPECIFICATIONS USING ALLOY*
Francisco Rebello de Andrade
1
, João Pascoal Faria
1,2
and Ana C. R. Paiva
1
1
Department of Informatics Engineering - Faculty of Engineering of the University of Porto, Porto, Portugal
2
INESC Porto, Rua Dr. Roberto Frias, s/n, 4200-465, Porto, Portugal
Keywords: Test case generation, Algebraic specifications, Abstract data types, Alloy analyzer.
Abstract: Algebraic specification languages have been successfully used for the formal specification of abstract data
types (ADTs) and software components, and there are several approaches to automatically derive test cases
that check the conformity between the implementation and the algebraic specification of a software
component. However, existing approaches do not assure the coverage of conditional axioms and conditions
embedded in complex axioms. In this paper, we present a novel approach and a tool to automatically derive
test cases from bounded algebraic specifications of ADTs, assuring axiom coverage and of all minterms in
its full disjunctive normal form (FDNF). The algebraic specification is first translated into the Alloy
modelling language, and the Alloy Analyzer tool is used to find model instances for each test goal (axiom
and minterm to cover), from which test cases in JUnit are extracted.
1 INTRODUCTION
Our society is increasingly dependent on the correct
functioning of software systems, so the software
industry should strive to deliver essentially defect
free software, by using more effective and efficient
defect prevention and detection techniques than are
in common use today. The automatic generation of
test cases from formal specifications should play an
important role in that effort, because of the higher
rigor, automation and thoroughness that is
introduced in the testing process, when compared to
manual test case generation (Bo et al., 2008, Chen et
al., 1998, Hughes and Stotts, 1996).
Amongst the existing formal specification
languages, algebraic ones are particularly well suited
for the generation of black-box tests, because the
syntax and semantics of the operations provided by a
software component are specified irrespective of
how its state is represented and manipulated
internally, contrarily to what happens with other
formal specification languages. A simple example of
an algebraic specification of an abstract data type
(ADT) (Guttag, 2002) is shown in Figure 1. The
semantics of operations is defined through axioms
that relate different operations, without any
assumption about how the state is represented
internally.
However, this very-high level of abstraction also
poses additional challenges for test case generation.
In fact, several approaches exist to automatically
derive test cases from algebraic specifications (Bo et
al., 2008, Chen et al., 2001, Chen et al., 1998, Dan
and Aichernig, 2005, Bernot et al., 1991, Kong et
al., 2007, Doong and Frankl, 1994), but they do not
assure the coverage of conditional axioms and
conditions that are part of complex Boolean
expressions, as explained in more detail in the state
of the art section of this paper.
To overcome such limitations, we use the Alloy
Analyzer tool and its constraint satisfaction
1: Sort
2: Stack
3: Operations
4: newStack:‐>Stack
5: push:StackInt‐>Stack
6: pop:Stack‐>Stack
7: ...
8: Axioms
9: StackS,IntE:S.push(E).pop()=S
10: ...
Figure 1: Excerpt of the Stack algebraic specification.
*Work supported by FCT under contract
PTDC/EIA/103103/2008
192
Rebello de Andrade F., Pascoal Faria J. and C. R. Paiva A..
TEST GENERATION FROM BOUNDED ALGEBRAIC SPECIFICATIONS USING ALLOY.
DOI: 10.5220/0003528101920200
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 192-200
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

capabilities (Jackson, 2011b, Jackson, 2011a,
Cunha, 2009, Anastasakis et al., 2008). The main
idea is to translate the algebraic specification into a
satisfiable Alloy model, according to a set of rules.
Then, the Alloy Analyzer is used to find model
instances that exercise specified axiom cases, from
which test cases are finally extracted using a
refinement mapping to the target implementation
language.
With this method, it is possible to generate tests
that guarantee coverage of all the minterms in the
axiom’s full disjunctive normal form (FDNF). The
method also allows checking the consistency of the
algebraic specification by examining the model
instances found by Alloy Analyzer.
The work presented in this paper is part of a
larger project aimed at improving the reliability of
software components (FCT, 2009), using ConGu
(Abreu et al., 2007b, Reis, 2007, Nunes et al., 2009)
as the algebraic specification language and Java as a
target implementation language.
The rest of the paper is organised as follows.
Section 2 presents the state of the art. Section 3
gives an overview of the test case generation
approach. Section 4 gives an overview of the
algebraic specification language used and the
refinement mapping to Java types. In section 5, the
translation rules and decisions made to convert the
algebraic specification modules into Alloy
specifications are explained. Section 6 describes
how test cases can be produced from the model
instances. Section 7 presents some conclusions and
future work. A simple running example is used to
illustrate the approach.
2 STATE OF THE ART
Three main techniques were found in the literature
to generate test cases based on algebraic
specifications (Mcmullin, 1982, Hughes and Stotts,
1996, Doong and Frankl, 1994, Bo et al., 2008, Chen
et al., 2001, Chen et al., 1998, Dan and Aichernig,
2005, Bernot et al., 1991, Kong et al., 2007): manual
scripting, term rewriting and variable substitution.
2.1 Manual Scripting
In manual scripting (Mcmullin, 1982, Hughes and
Stotts, 1996) the user supplies the values and terms
to exercise for each free variable, and a tool
substitutes each possible combination of values in
the axioms. This approach involves too much
manual work, is prone to errors and omissions, and
may cause a combinatorial explosion of test cases.
2.2 Term Rewriting
Term rewriting proposes that permissible term
expressions be generated at random using the
methods and operations of an algebraic
specification, and then rewritten into their
necessarily unique normal form, using the algebraic
specification’s axioms as rewriting rules (Doong and
Frankl, 1994). This way, one may build test cases by
checking if the legal terms generated and the normal
form terms are equivalent. Considering the push and
pop operations and the axiom in Figure 1, the three
steps involved are illustrated in Figure 2.
Step1:Generatetermexpression
newStack.push(3).push(7).pop()
Step 2: Reduce to normal form using axioms as
rewritingrules
newStack.push(3).push(7).pop()Æ
newStack.push(3)
Step3:Produceassertion
newStack.push(3).push(7).pop() =
newStack.push(3)
Figure 2: Test case generation using term rewriting.
One of the problems to overcome with this
method is how to generate the initial term
expressions in an automated way, when operation
domains and conditional axioms are present.
Another problem, which is put up by the author of
(Doong and Frankl, 1994), is how to deal with these
initial term expressions when they do not hold a
unique normal form equivalent – in a set you may
have the axiom set1.insert(a).insert(b) =
set1.insert(b).insert(a). A possible solution to this
problem may be to generate several test assertions.
2.3 Variable Substitution
Variable substitution suggests going through each
axiom and substituting its variables with randomly
generated type instances and term expressions made
up of constructive operations only – the same as
saying normal form term expressions (Bo et al.,
2008, Chen et al., 2001, Chen et al., 1998, Dan and
Aichernig, 2005, Bernot et al., 1991, Kong et al.,
2007). Figure 3 shows an example considering the
same algebraic specification excerpts as in Figure 1.
TEST GENERATION FROM BOUNDED ALGEBRAIC SPECIFICATIONS USING ALLOY
193

Although this method has the advantage that each test
case generated exercises a well identified
Step 1: Pick
axiom
StackS,IntE:S.push(E).pop()=S
Step 2: Generate expressions and primitives for
variables
S=newStack.push(7)
E=3
Step3:Produceassertion
newStack.push(7).push(3).pop()=newStack.push(7)
Figure 3: Test case generation using variable substitution.
axiom, the random generation process may be
unable to generate combinations of values that
satisfy conditions in conditional axioms, multi-
conditional axioms (if-then-else and if-and-only-if),
and complex Boolean expressions.
2.4 Automatic Test Case Generation
with Alloy
TestEra (Khurshid and Marinov, 2003, Khurshid and
Marinov, 2004) is a tool which generates input
values to test Java programs from pre-conditions
given as first-order relational formulas in the Alloy
modelling language. First, it generates all non-
isomorphic instances to find the possible inputs for a
Java method, using the available Alloy
pre-conditions for a given bound, and converts these
inputs to Java – concretisation translation.
Afterwards, it runs the Java method with these input
values and converts the outputs obtained back to
Alloy – abstraction translation – to verify the
correctness of each input/output pair by evaluating a
formula that represents the method post-condition.
Although the concretisation translation is quite
interesting, and quite similar to the problem to tackle
in this paper, the goal is to translate the whole
instances found by Alloy to Java as test cases –
sequences of operations with corresponding input
values – and not only input variables.
3 METHOD AND TOOL
OVERVIEW
This section gives an overview of the approach
proposed in this paper. The workflow diagram is
shown in Figure 4.
First of all, the ConGu algebraic specification
and the refinement mapping file – explained later on
in section 4 – are inputs of the ConGu’s Parser
which creates an in-memory object representation of
the algebraic specification and refinement mapping.
This representation is translated into Alloy by the
new Alloy Translator tool, according to a set of
translating rules. A set of run commands are
automatically generated by the tool to exercise all
minterms in the full disjunctive normal form
(FDNF) of each axiom. More detail is provided in
section 5.
Afterwards, Alloy Analyzer reads the outputted
Alloy specification and executes each of the run
commands at a time. Each model instance found by
Alloy Analyzer satisfying a run command is
exported into a XML format. The test generator tool
receives the XML representation of the model
instances found and the in-memory representation of
the refinement mapping as input, and generates
corresponding JUnit test cases. More in-depth
explanation of this step can be found in section 6.
Figure 4: Overview of the test generation process.
4 ALGEBRAIC SPECIFICATION
AND REFINEMENT MAPPING
WITH CONGU
This section explains how the algebraic specification
and the refinement mapping to Java classes, and
interfaces, are organised in ConGu (Nunes et al.,
2009).
ConGu supports sub-sorting, i.e., the
specification of sorts that extend other sorts.
Implicitly, all sorts are ultimately a sub-sort of the
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
194

implicitly existent ConGu sort Element.
In a ConGu specification there are three types of
operations (Abreu et al., 2007a): constructors,
observers and others. Constructors consist of a
minimal number of operations needed to build any
possible value of the sort, while observer operations
are operations used to analyze the value of a sort. As
for other operations, these are defined as being
derived from the first two previously defined
operations or comparing operations. The
constructors can also be divided into two types: the
creators, that do not have parameters of the sort
type they instantiate, and transformers, that are the
remaining constructors that have at least the first
parameter of the same sort type as its output, called
self argument. All non-constructor operations have
the self argument.
After the declaration of the several types of
operations, there is a section called “domains” to
restrict the domain of partial operations.
An example of a ConGu specification for a
bounded stack of integers (with limited size) is
shown in Figure 5. The size limitation makes the
corresponding Alloy model satisfiable by finite
instances.
1: specificationBStackInt
2: sorts
3: BStackInt
4: constructors
5: make:int‐‐>BStackInt;//Creator
6: push:BStackIntint‐‐>BStackInt;//Transformer
7: observers
8: peek:BStackInt‐‐>?int;
9: pop:BStackInt‐‐>?BStackInt;
10: size:BStackInt‐‐>int;
11: maxSize:BStackInt‐‐>int;
12:
others
13: empty:BStackInt;
14: domains
15: S:BStackInt;
16: E:int;
17: peek(S)ifnotempty(S);
18: pop(S)ifnotempty(S);
19: push(S,E)ifsize(S)<maxSize(S);
20: axioms
21: S:BStackInt;
22: E,N:int;
23: peek(push(S,E))=Eifsize(S)
<maxSize(S);
24: pop(push(S,E))=Sifsize(S)<maxSize(S);
25: size(make(N))=0;
26: size(push(S,E))=1+size(S)ifsize(S)<maxSize(S);
27: empty(S)iffsize(S)=0;
28: maxSize(make(N))=N;
29: maxSize(push(S,E))=maxSize(S)
30: ifsize(S)<maxSize(S);
31: endspecification
Figure 5: ConGu algebraic specification of a bounded
stack of integers.
For mapping sorts to Java classes, there are files
called refinement mapping files, in charge of
associating each sort and its predicates and
operations to the respective Java class and methods.
Figure 6 is the possible Java class – StackInt – the
BStackInt sort would correspond to.
So, having the ConGu specification and knowing
the corresponding types desired, the refinement
mapping would be the one represented in Figure 7.
1: publicclassStackInt{
2: publicStackInt(intmax){...}
3: publicvoidpush(inte){...}
4: publicintpeek(){...}
5: publicvoidpop(){...}
1: publicintsize(){...}
2: publicintmaxSize(){...}
3: publicbooleanisEmpty(){...}
4: ...
5: }
Figure 6: Skeleton of a Java implementation of a Stack of
integers.
1: refinement
2: BStackIntisStackInt{
3: make:n:int‐‐>BStackIntisStackInt(intn);
4: push:BStackInt e:int‐‐>BStackInt is void
push(inte);
5: peek:BStackInt‐‐>?intisintpeek();
6: pop:BStackInt‐‐>?BStackIntisvoidpop();
7: size:BStackInt‐‐>intisint
size();
8: maxSize:BStackInt‐‐>intisintmaxSize();
9: empty:BStackIntisbooleanisEmpty();
10: }
Figure 7: Stack of integers’ refinement mapping.
5 TRANSLATION TO ALLOY
This section presents the rules followed by the
developed tool to translate algebraic specifications,
written in ConGu, to Alloy specifications. We
assume the reader is familiar with Alloy. For an
introduction please see (Jackson, 2011b).
Requirements to take into consideration before
going further are:
• The resulting Alloy specification should be
satisfiable by finite models in order to enable
Alloy Analyzer to find model instances;
• The resulting Alloy specification should be
consistent with the algebraic specification;
• Sorts should include, at least, two constructors:
one creator and one transformer. These
constructors should exist in order to extract state
TEST GENERATION FROM BOUNDED ALGEBRAIC SPECIFICATIONS USING ALLOY
195

transitions of the sort type from the Alloy model
instances and generate test cases.
The first two points may conflict with each
other. The first one requires the manipulation of the
algebraic specification in order to generate finite
Alloy specifications. This was performed for the
stack of integers by imposing a limit on its size.
Additional constraints introduced in the Alloy
specification will be described later on.
In the sequel it will be described how sorts,
operation domains and axioms are translated from
the algebraic specification to Alloy, and how the test
goals are specified as run commands in Alloy.
5.1 Signatures
Each sort of the algebraic specification is translated
into a signature in Alloy, with its operations and
predicates as relations, according to a set of rules
summarized in Table 1, found in the appendix, and
illustrated in this section through the examples.
Figure 8 presents the translation to Alloy of the
syntactic part of the algebraic specification of the
bounded Stack of integers, according to the rules in
Table 1.
Figure 8: Alloy signatures generated for the bounded stack
of integers.
Sorts. All non-primitive signatures extend the
Element signature, represented in line 1 in Figure 8,
which has no relations and represents the Element
sort in ConGu (see rules R1, R2 and R3 in Table 1).
Operations (except creator constructors). All
operations (except creator constructors) are
represented as fields (relations) of the signature
corresponding to the original sort. Since the self
argument represents the sort the operation is applied
to, it does not appear as an argument.
An operation that only has the self argument as
an argument, in Alloy, becomes a single relation to
an instance of the signature that represents the
output sort of the operation (R4 in Table 1). An
example of this case, in the bounded Stack of
Integers example, is the ¯¤¤ª operation.
An operation that has more arguments than the
self argument requires a multirelational field,
relating the signature instances of the arguments of
the operation with its output parameter (R4 in Table
1).
Predicates. Predicates obey these same rules except
that the outputs of the resulting relations are always
a Boolean signature instance (R5 in Table 1). An
example, in the Stack example, is the empty
predicate.
Partial Operations and Predicates. Relations
translated from operations or predicates that have a
restricted domain, create lone (one or none) type
relations (R6 in Table 1). The reason to generate
lone type relations from an operation with a
restricted domain is to only allow relations to exist
within that domain. An example of an operation with
a restricted domain is pop.
Creator Constructors. Creator constructors
generate a lone relation in the signature named start,
which has one instance of itself in every model
instance generated and is the source of all the
signature instances (R7 and R8 in Table 1). An
example of a creator constructor is make.
Argument Sorts of Constructor Operations. In
order to guarantee that the Alloy specification is
satisfiable by finite model instances, the domain of
each argument of each constructor (except the self
argument) is constrained to belong to a finite set.
Those sets are declared as fields of the start
signature (rule R9 in Table 1), and facts are added to
restrict the arguments’ domains to those sets.
Domain restriction conditions are implicitly applied
to all the axioms that refer those constructors (to be
described in the sequel). Examples for the push and
make constructors are shown in lines 14-15 in
Figure 8.
5.2 Signature Restraining Facts
Next, basic signature restraining facts to ensure that
model instances are consistent with the original
algebraic specification will be described.
In the algebraic specification, the instances of the
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
196
sorts are implicitly constrained to the ones that may
be constructed by a constructor term expression,
starting with a creator constructor operation. When
translating the algebraic specification to Alloy, this
assumption must be made explicit by defining
signature binding facts to avoid generating
inconsistent instances wrt the original algebraic
specification. For example, the instances of the core
signature – signature correspondent to the sort to be
tested – reached only by using at least one observer
operation – like the pop operation – could turn the
model instance inconsistent wrt the original
algebraic specification. So, starting from the start
signature instance, all instances of core signatures
must be reached through constructor relations.
The fact to impose this constraint, in the case of
the bounded stack of integers, is shown in lines 1-5
in Figure 9, following the rule in Table in the
appendix. This fact imposes that all instances of the
stack are generated by using the creator constructor
make, followed by 0 or more applications of the
transformer constructor push.
1: factBStackIntConstruction{
2: BStackIntin
3: (start.make[Int]).*
4: {x:BStackInt,y:x.push[Int]}
5: }
6:
7:
factElementUsedVariables{
8:
Elementin(BStackInt)
9:
}
Figure 9: Signature restraining facts generated for the
bounded stack of integers.
In order to remove from the equation model
instances with unrelated instances of non-core
signatures – Element in the example –, another fact
is written. In this fact, either a non-core signature
instance is being used as the input or output of a core
signature’s relation or the instance at hand is an
instance of a sub-signature of this signature, as can
be seen in Table , in the appendix. Lines 7-9 in
Figure 9 show the fact generated for the Element
signature.
5.3 Axioms and Domains
Now we will explain the translation of the semantic
part of the algebraic specification, i.e., axioms and
domains, to facts.
Axioms. Each axiom is translated to a fact in Alloy.
First, the free variables used in the axiom originate
universally quantified variables over the
corresponding signatures in Alloy. Then, if the
axiom expression involves constructors with
non-self arguments, pre-conditions are introduced to
restrict their domains to the finite sets declared in the
start signature (see section 5.1). Done this, the
axiom expression is laid down. The rule is described
in Table , in the appendix, and an example is
presented in Figure 10.
1: factaxiomBStackInt1{
2: allE:Int,S:BStackInt|
3: (Einstart.pushInt0)implies(
4: (S.size<S.maxSize)implies(S.push[E].pop=
S))
5: }
Figure 10: Alloy fact generated for the axiom in line 24 of
Figure 5.
As can be seen, conditional axioms are treated as
implications. As for the else and iff tokens, of the
ternary conditional and biconditional axioms, they
remain unaltered in Alloy since these tokens exist in
Alloy and mean the same as they do in ConGu.
Domains. Each domain restriction (for a partial
operation) is translated also to a fact in Alloy. The
variables used in a domain fact are declared in the
same manner as with axioms. When the declared
pre-condition in the domain declaration evaluates to
false, or the non-self arguments of the constructors
appearing in that pre-condition are outside the
domain declared in the start signature, the
corresponding lone relation in Alloy becomes
nonexistent. Otherwise, the relation must exist.
The rule is described in Table and an example is
presented in Figure 11.
1: factdomainBStackInt2{
2: allE:Int,S:BStackInt|
3: (S.size<S.maxSizeandEinstart.pushInt0)
4: impliesoneS.push[E]elsenoS.push[E]
5: }
Figure 11: Alloy fact generated for the domain restriction
in line 19 of Figure 5.
5.4 Generation of Run Commands for
Exercising Axioms
Our default test coverage criterion is to generate a
test case for each minterm in the FDNF
representation of each axiom (see Table 5 in the
appendix). Although not all minterms are necessarily
satisfiable, at least one minterm should be satisfiable
for each axiom.
TEST GENERATION FROM BOUNDED ALGEBRAIC SPECIFICATIONS USING ALLOY
197
For each axiom and minterm, in order to find
bindings of the axiom’s free variables that satisfy the
minterm, a run command is generated in a
straightforward way as illustrated in Figure 12.
There is one configurable complexity variable
that may be defined when performing a run
command with the developed tool. This variable,
called max, defines the maximum allowed number
of instances for each signature in a model instance.
In this example, this variable was set to 7 (seven).
1: runrun_axiomBStackInt4_0{
2: someS:BStackInt|
3: (S.empty=BOOLEAN/True)and(S.size=0)
4: }for7
5:
6: runrun_axiomBStackInt4_1{
7: someS:BStackInt|
8: (S.empty=BOOLEAN/False)and(S.size!=0)
9: }for7
Figure 12: Run commands generated for exercising
axiomBStackInt4 (see line 27 of Figure 5).
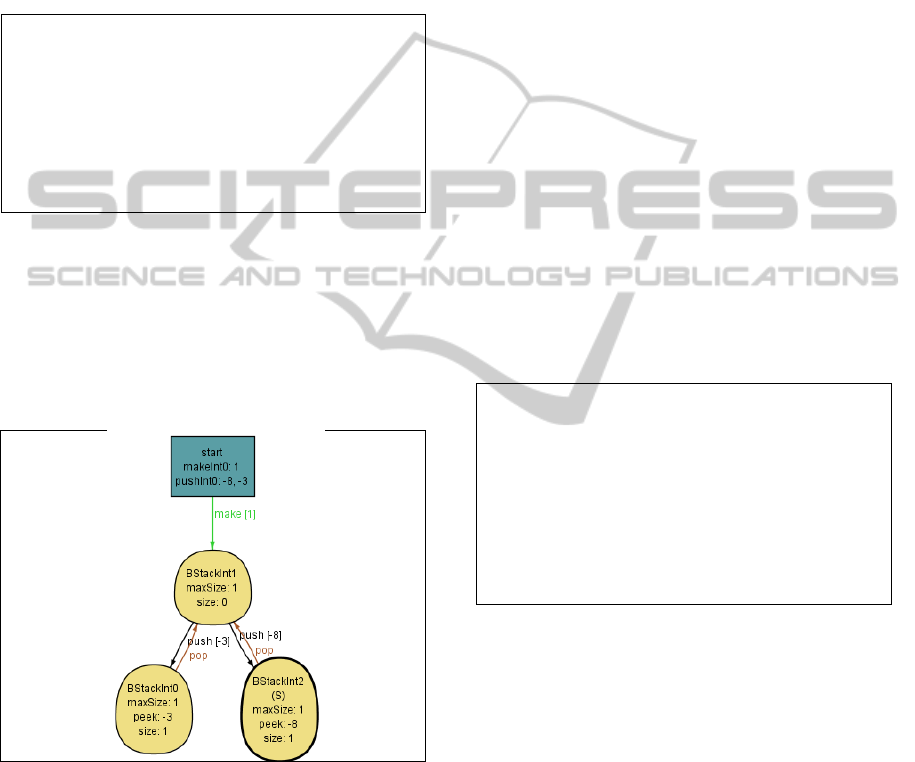
A graphical representation of a model instance
found by Alloy Analyzer when a run command is
executed is shown in Figure 13. The diagram shows
clearly how the free variables are instantiated (S in
this example) and how the axiom is exercised.
Figure 13: Model instance found by Alloy Analyzer when
the run_axiomBStackInt4_1 command is executed.
6 EXTRACTION OF JUNIT TEST
CASES FROM ALLOY
This section describes how test cases in JUnit (Beck
et al.) are extracted from the model instances found
by Alloy Analyzer.
As explained before, for each minterm of each
axiom, it is generated a run command that, when
executed by Alloy Analyzer, will find a model
instance and bindings for the axiom’s free variables
that satisfy the minterm. The model instance found
is exported to XML and subsequently interpreted (as
a Finite State Machine) by the test extractor tool, to
find shortest paths for constructing the axiom
variables.
The refinement mapping from the algebraic
specification to Java (see section 4) is used to
produce a proper encoding of the test cases in Java.
An example of a test case extracted from the
model instance in Figure 13 is shown in Figure 14.
The test code generated has two parts: a setup
part, where the variables involved in the axiom are
constructed (according to the model instance found
by Alloy Analyzer), and an axiom verification part,
where the specific minterm of the axiom is checked
(as specified in the run command). To construct each
variable, it is followed a shortest path in the model
instance, from the start signature instance to the
node bound to that variable. In the axiom
verification part, it is generated a separate assertion
for each operand of the minterm (conjunction) being
exercised, for better fault localization.
1: @Test
2: publicvoidtest_axiomBStackInt4_1(){
3: //setup
4: StackIntBStackInt1=newStackInt(1);
5: StackIntBStackInt2=BStackInt1.push(‐8);
6: StackIntS=BStackInt2;
7: //axiomverification
8: assertTrue(!S.isEmpty());
9: assertTrue(S.size()!=0);
10: }
Figure 14: JUnit test case corresponding to the second run
command of Fig. 12 and the model instance in Fig. 13,
using the refinement mapping in Figure 7.
Equality axioms, such as pop(push(S,E))=S, are
checked with assertEquals, which in turn uses the
equals method in Java, so the approach relies on the
correct implementation of equals.
7 CONCLUSIONS
An approach was described to automatically
generate JUnit test cases from algebraic
specifications of ADTs, using an intermediate
translation to Alloy. In this approach, a test case is
generated for each minterm of the FDNF
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
198

representation of each axiom. Reasoning about the
Alloy model allows also checking the consistency of
the algebraic specification itself. Although, for space
constraints, the example presented in the paper is
very simple, the method has been successfully
applied to several other ADTs, such as the Sorted
Set and Priority Queue.
A common limitation of Alloy Analyzer is
scalability, because of the time required to find
model instances in complex cases. However, we did
not found this to be a problem for testing ADTs in
our approach. On a 32 bit Intel Core 2 Duo T6600 @
2.2 GHz with 3 GB of RAM, running Windows 7,
Alloy Analyzer took around 100 seconds to run the
17 axiom cases of the bounded stack. Times of the
same magnitude were obtained for other ADTs.
As future work, we intend to consolidate the test
case extractor tool, integrate the complete tool suite
into the ConGu’s plug-in for Eclipse (Eclipse
Foundation, 2010, Vasconcelos et al., 2008),
experiment the approach with more ADTs,
demonstrate the adequacy of the test cases generated
by mutation testing, and support unbounded ADTs
by finding automatically safe bounds applicable.
REFERENCES
Abreu, J., Caldeira, A., Lopes, A., Nunes, I., Reis, L. S. &
Vasconcelos, V. T. 2007a. Congu, Checking Java
Classes Against Property-Driven Algebraic
Specifications.
Abreu, J., Vasconcelos, V. T., Nunes, I., Lopes, A., REIS,
L. S. & Caldeira, A. 2007b. ConGu v.1.50 The
Specification and the Refinement Languages.
Anastasakis, K., Behzadbordbar & Kuster, J. M. 2008.
Analysis of model transformations via Alloy.
Beck, K., Gamma, E. & Saff, D. JUnit's project
homepage, http://junit.sourceforge.net/ [Online].
Available: http://junit.sourceforge.net/ [Accessed].
Bernot, G., Gaudel, M. C. & Marre, B. 1991. Software
testing based on formal specifications: a theory and a
tool. Softw. Eng. J.: Michael Faraday House.
Bo, Y., Liang, K., Yufeng, Z. & Hong, Z. Year. Testing
Java Components based on Algebraic Specifications.
In: International Conference on Software Testing,
Verification, and Validation, 2008 Washington, DC,
USA. IEEE Computer Society, 190-199.
Chen, H. Y., Tse, T. H., Chan, F. T. & Chen, T. Y. 1998.
In black and white: an integrated approach to class-
level testing of object-oriented programs. ACM Trans.
Softw. Eng. Methodol.: ACM.
Chen, H. Y., Tse, T. H. & Chen, T. Y. 2001. TACCLE: a
methodology for object-oriented software testing at the
class and cluster levels. ACM Trans. Softw. Eng.
Methodol.: ACM.
Cunha, A. 2009. 'An introduction to Alloy' slides.
Dan, L. & Aichernig, B. K. 2005. Combining Algebraic
and Model-Based Test Case Generation.
Doong, R.-K. & Frankl, P. G. 1994. The ASTOOT
approach to testing object-oriented programs. ACM
Trans. Softw. Eng. Methodol.: ACM.
Eclipse Foundation, I. 2010. Eclipse's website,
http://www.eclipse.org/ [Online]. Available:
http://www.eclipse.org/ [Accessed].
FCT 2009. A Quest for Reliability in Generic Software
Components.
Guttag, J. V. 2002. Abstract data types, then and now.
Software pioneers: contributions to software
engineering. Springer-Verlag New York, Inc.
Hughes, M. & Stotts, D. 1996. Daistish: systematic
algebraic testing for OO programs in the presence of
side-effects. Proceedings of the 1996 ACM SIGSOFT
international symposium on Software testing and
analysis. San Diego, California, United States: ACM.
Jackson, D. 2011a. Alloy Analyzer's API,
http://alloy.mit.edu/alloy4/public/ [Online]. Available:
http://alloy.mit.edu/alloy4/public/ [Accessed].
Jackson, D. 2011b. Alloy Analyzer's website,
http://alloy.mit.edu/ [Online]. Available:
http://alloy.mit.edu/ [Accessed 11-06-2010].
Khurshid, S. & Marinov, D. 2003. TestEra: A Novel
Framework for Testing Java Programs.
Khurshid, S. & Marinov, D. 2004. TestEra: Specification-
based Testing of Java Programs Using SAT.
Kong, L., Zhu, H. & Zhou, B. 2007. Automated Testing
EJB Components Based on Algebraic Specifications.
Proceedings of the 31st Annual International
Computer Software and Applications Conference -
Volume 02. IEEE Computer Society.
Mcmullin, P. R. 1982. Daists: a system for using
specifications to test implementations. University of
Maryland at College Park.
Nunes, I., Lopes, A. & Vasconcelos, V. 2009. Bridging
the Gap between Algebraic Specification and Object-
Oriented Generic Programming.
Reis, L. S. 2007. ConGu v.1.50 User’s Guide.
Vasconcelos, V. T., Nunes, I., Lopes, A., Ramiro, N. &
Crispim, P. 2008. Monitoring Java Code Using
ConGu.
APPENDIX
Table 1: Translation rules from ConGu (syntax) to Alloy.
Rule AlgebraicSpec
(ConGu)
Alloy
R1. Roottype
(implicit) sigElement{}
R2. Type
sortsS sigSextends
Element
R3. Subtype
sortsS<S’ sigSextendsS’
R4. Total
operation
(exceptcreator
constructors)
o:S‐‐>t’
o:Sxt
1
x…xt
n
‐‐
>t’
o:onet’
o:(t
1
‐>...‐>t
n
)‐>one
t’
TEST GENERATION FROM BOUNDED ALGEBRAIC SPECIFICATIONS USING ALLOY
199

Table 1: Translation rules from ConGu (syntax) to
Alloy(Cont.).
R5. Total
predicate
p:S
p:Sxt
1
x...xt
n
p:one
BOOLEAN/Bool
p:(t
1
‐>...‐>t
n
)‐>
oneBOOLEAN/Bool
R6. Partial
operationor
predicate
(exceptcreator
constructors)
(withdomain
restriction)
SameasR4andR5,
withloneinsteadof
one
R7. Start
instance
(notdefined) onesigstart
R8. Creator
constructor
c:t
1
x...xt
n
‐‐>Sc:(t
1
‐>...‐>t
n
)‐>lone
S
(insidesigstart)
R9. Non‐self
argumentsof
constructor
operations
Transformer:
c:S
xt
0
x...xt
n
‐‐
>S
Creator:
c:t
0
x...xt
n
‐‐
>S
ct1:sett
0
...
ctn:sett
n
(insidesigstart)
Table 2: Rule for the construction fact.
Algebraicspecification
CoresortSwithcreatorconstructors
c
i
:s
i1
x...xs
ik
i
‐‐>S(i=1,…,n)
andtransformerconstructors
t
j
:Sxs'
j1
x...xs'
jw
j
‐‐>S(j=1,…,m).
Alloyconstructionfact
factSConstruction{
Sin(start.c
1
[s
11
]…[s
1k
1
]+…+start.c
n
[s
n1
]…[s
nk
n
]).*
{x: S, y: x.t
1
[s’
11
] … [s’
1w
1
] + … + x.t
m
[s’
m1
] …
[s’
mw
m
]}
}
Table 3: Rule for usage fact.
Algebraicspecification
Non‐core sort S (including root sort Element) with n
occurrencesasinputoroutputparameterofoperationsofcore
signatures
f
i
:s
i1
x…xs
iw
i
‐1
‐‐>s
iw
i
definedinsortS
i
(i=1,…,n)
where S or a supertype of S occurs in position k
i
of the
input/outputparameterlist,with1
≤
k
i
≤
w
i
.
Additionally, the non‐core Ssort may havedirectsubtypes T
1
,
…,T
m
.
Predicates are treated as operations with output type
BOOLEAN/Bool.
Alloyusagefact
factSUsedVariables{
Sin(S
1
.f
1
[s
11
]…[s
1k
1
‐1
].s
1w
1
.s
1w
1
‐1
.….s
1k
1
+1
+…+
S
n
.f
n
[s
n1
]…[s
nk
n
‐1
].s
nw
n
.s
nw
n
‐1
.….s
nk
n
+1
+T
1
+…+T
m
)
}
Table 4: Rules for axiom and domain facts.
Constraint(ConGu) Fact(Alloy)
k
th
axiominsortS:
v
1
:S
1
;...;v
n
:S
n
;
formula(v
1
,...,v
n
);
factaxiomSk{
allv
1
:S
1
,...,v
n
:S
n
|
argTesting(formula’))
impliesformula’(v
1
,...,v
n
)
}
k
th
domaininsortS:
v
1
:S
1
;...;v
n
:S
n
;
op(v
1
,...,v
n
)if
cond(v
1
,...,v
n
);
factdomainSk{
allv
1
:S
1
,...,v
n
:S
n
|
(cond’(v
1
,...,v
n
)and
argTesting(op’))
impliesoneop’(v
1
,...,v
n
)
elsenoop’(v
1
,...,v
n
)
}
Table 5: Cases to exercise in conditional axioms and
constituent Boolean expressions.
Axiomorconstituent
Booleanexpression
Casestoexercise
(mintermsoftheFDNF)
Conditionalaxiom:
BifA
AandB
notAandB
notAandnotB
Logicaldisjunction:
AorB
AandB
AandnotB
notAandB
Biconditionalaxiom:
AiffB
AandB
notAandnotB
Ternaryconditional:
X=YwhenAelseZ
Previousrulesforthepair:
X=YifA
X=ZifnotA
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
200
