INTELLIGENT FAULT DETECTION, IDENTIFICATION AND
CONTROL OF SATELLITE FORMATION FLYING
Junquan Li and K. D. Kumar
Aerospace Engineering, Ryerson University, 350 Victoria Street, Toronto, Canada
Keywords:
Fault detection and fault tolerant control, Fuzzy logic system, Variable structure techniques, Satellite forma-
tion.
Abstract:
A class of nonlinear leader-follower satellite formation flying system subject to uncertain thruster faults and
external J
2
disturbances has been studied in this paper with the help of FDI and second order sliding mode
control. The faults considered are modeled as constant and time-varying faults which can occur randomly. It
is proved that the proposed control scheme can guarantee all signals of the closed-loop system to be semi-
globally, uniformly, and ultimately bounded, and the tracking error can converge to a small neighborhood
near zero. Simulation results confirm that the suggested control methodologies yield high formation keeping
precision and effectiveness for leader-follower formation flying systems. The numerical results demonstrate
the effectiveness of the proposed active fault tolerant control under thruster faults.
1 INTRODUCTION
Satellite formation flying (SFF) has been identified as
a significant technology for many different space mis-
sions. Environmentalforces such as gravitational per-
turbation, atmospheric drag, solar radiation pressure
and electromagnetic forces will cause the formation
to deviate from the desired trajectory. A low thrust
control system for autonomous coordinated multiple
satellite formation flying has been studied in great de-
tail. Events such as malfunctions in thrusters, sensors,
or other system components can cause severe perfor-
mance deterioration and system instability leading to
catastrophic accidents. The benefits of formation fly-
ing can only become available with a robust and reli-
able fault tolerant control system which is capable of
handling potential failures in these systems in order
to provide desirable performance (Valdes and Kho-
rasani, 2010) (Edwards et al., 2007) (Wu and Saif,
2007) (Azizi and Khorasani, 2008). According to a
recent survey paper (Benosman, 2010), many inter-
esting results have been obtained so far. But work that
treats both problems together of nonlinear fault detec-
tion and diagnosis and nonlinear fault tolerant con-
trol in an effective applicable method, is still missing.
Real-life applications of those nonlinear fault tolerant
control theories are also a missing part of the recent
work. The primary focus of this paper is on devel-
oping an intelligent fault tolerant control system for
satellite formation flying. The intelligent controller
has the ability to adapt the control to the mostly non-
linear process behavior and performs a fault diagno-
sis to request maintenance and a decision. Active
fault tolerant control based on a fuzzy logic system
and second order sliding mode observer is developed
from the Lyapunov theorem. Compared to other con-
trol methods, the proposed control method uses less
fuel.
2 SYSTEM MODEL
The satellites are modeled as point masses and there-
fore the rotational dynamics of the leader and follower
satellite are not taken into account. The orbital equa-
tions of motion for the leader satellite and the full
nonlinear translational dynamics of the followersatel-
lite relative to the leader satellite (shown in Figure 1),
taking into account the thrust and disturbance forces,
can be written in the following form (Wong et al.,
2002): Rewrite the MIMO formation flying system
as
˙
X(t) =

X
2
(t)
f(t,X, u)

+ D(t, X,u) (1)
X(t) =

X
1
(t)
X
2
(t)

∈ R
6
, X
1
(t) ∈ R
3
, X
2
(t) ∈ R
3
.
85
Li J. and D. Kumar K..
INTELLIGENT FAULT DETECTION, IDENTIFICATION AND CONTROL OF SATELLITE FORMATION FLYING.
DOI: 10.5220/0003529600850090
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 85-90
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Geometry of orbit motion of leader and follower
satellites.
The system model given in Equation 1 with
thruster fault is represented as
˙
X(t) =

X
2
(t)
f(t, X,u)

+

O
n×n
g(t, X,u)

+ D(t, X,u)
(2)
where g(t, X,u) represents the unknown thruster fault
and is bounded.
The normal controller objective (u
n
) for forma-
tion keeping of the follower satellite relative to the
leader satellite requires that the actual position of the
follower track the desired relative position trajectory.
Third, all signals in the closed-loop system are uni-
formly, and ultimately bounded. The tracking errors
converge to a small neighborhood near zero.
3 FAULT DETECTION AND
ACCOMMODATION SCHEME
We now summarize a methodology for designing a
fault detection and accommodation scheme, which
consists of a second order sliding mode observer and
fuzzy identifier. The proposed fault accommodation
scheme is designed such that it is capable of detecting
and identifying unknown faults.
3.1 Fault Detection and Isolation
Scheme
The intelligent and learning based techniques (Neu-
ral network, fuzzy logic, and expert system) are more
suitable and promising when accurate mathematical
models are not available. These methods monitor and
approximate any fault behaviorin the dynamic system
by using on-line approximation and adaptive nonlin-
ear estimation techniques. Fault detection and isola-
tion schemes (FDI) have been researched extensively
although few efforts have been made in the area of au-
tonomous fault tolerant control systems for formation
flying of satellites.
A second order sliding mode observer with fuzzy
identifier scheme is proposed in this paper, based on
the second order sliding mode observer with wavelet
networks scheme proposed in (Wu and Saif, 2007).
3.1.1 Fault Detection by Second Order Sliding
Mode Observer
The second order sliding mode observer is used to ob-
serve the system states with modeling uncertainties
and disturbance prior to the occurrence of any fault.
Based on Equation 1, a nonlinear observer is proposed
as
˙
ˆ
X
1
=
ˆ
X
2
+ λ
1
(3)
˙
ˆ
X
2
= f(t, X
1
,
ˆ
X
2
,u) + λ
2
(4)
where
ˆ
X
1
and
ˆ
X
2
are the state estimations, λ
1
andλ
2
are the correction variables.
The correction variables λ
1
and λ
2
are of the form
λ
1
= ρ


˜
X
1


0.5
tanh(
˜
X
1
) (5)
λ
2
= σ
1
tanh(
˜
X
1
) (6)
Taking the estimation errors as
˜
X
1
= X
1
−
ˆ
X
1
and
˜
X
2
= X
2
−
ˆ
X
2
(residual), the error equations are writ-
ten as
˙
˜
X
1
=
˜
X
2
− ρ


˜
X
1


0.5
tanh(
˜
X
1
) (7)
˙
˜
X
2
= G(t, X
1
,X
2
,
ˆ
X
2
,u) − σ
1
tanh(
˜
X
1
) (8)
where G(t, X
1
,X
2
,
ˆ
X
2
,u) = g(t, X
1
,X
2
,U(t,X
1
,X
2
)) −
g(t, X
1
,
ˆ
X
2
,U(t,X
1
,X
2
)) + D(t,X
1
,X
2
,U(t,X
1
,X
2
)).
According to the reference (Davila et al., 2005), G is
assumed to be bounded and ρ, σ
1
can be chosen by


G(t, X
1
,X
2
,
ˆ
X
2
,u)


< g
∗
ρ >
s
2
σ
1
− g
∗
(σ
1
+ g
∗
)(1+ η)
1− η
σ
1
> g
∗
(9)
where η is a constant (0 < η < 1).
We can find


˜
X
1


≤
˜
X
M
(threshold bound chosen
by experiments). The decision for detecting a fault is
made when


˜
X
1


exceeds its threshold bound
˜
X
M
.
3.1.2 Fault Isolation by Fuzzy Identifier
For a real nonlinear system, it is quite difficult to de-
termine a priori what class of faults may occur. As the
fault is unknown, it is also difficult to isolate the fault
function. Therefore, we only present constant fault
functionsin this paper. In future work, we will give all
possible fault functions (constant, time-varying, and
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
86

ramp fault) for finding a fault type. The isolation ob-
servers corresponding to one of the possible types of
faults are proposed as
˙
ˆ
X
r1
=
ˆ
X
r2
+ λ
1
(10)
˙
ˆ
X
r2
= f(t,X
r1
,
ˆ
X
r2
,u) + λ
2
+ γ(t − T f) ˆg (11)
where
ˆ
X
r1
and
ˆ
X
r2
are the state estimations for one of
the possible types of faults, λ
1
andλ
2
are the correc-
tion variables, and ˆg is a fuzzy identifier to specify the
process fault. The term T f is the time to activate the
fuzzy identifier.
In this paper, a fuzzy identifier (Wang, 1997) is
used to determine the fault location and to estimate
its magnitude. The fuzzy logic system is a collection
of IF-THEN fuzzy rules such as:
R
k
: IF x
1
is A
k
1
, and, · ·· , x
n
is A
k
n
, (12)
THEN y is B
k
.
The output of the fuzzy system (using singleton
fuzzification, product inference and center average
defuzzification) can be written as :
y
out
=
∑
P
l=1
θ
l
F
(X)
∏
N
i=1
µ
l
Ai
l
(x
i
)
∑
P
l=1
∏
N
i=1
µ
l
Ai
l
(x
i
)
= θ
T
ξ (13)
where P is the total fuzzy rules number, the member-
ship functions µ
A1
l
(x
1
)
,..., µ
An
N
(x
n
)
(N is the number of
membership functions) are Gaussian functions, and ξ
is the fuzzy basis function

ξ
l
(x) =
∏
N
i=1
µ
Ai
l
(x
i
)
∑
P
l=1
∏
N
i=1
µ
Ai
l
(x
i
)

.
We use the fuzzy system ˆg(t, X,u | θ
g
) = θ
T
g
ξ
g
(t, X,u)
to approximate g(t,X,u).
It is assumed that there exists an optimal fuzzy
logic system to learn the nonlinear terms g(t,X,u)
such that
g(t, X,u) − g
∗
(t, X,u | θ
∗
g
) = w
G
(t, X,u) (14)
where w
G
is approximation error and is bounded. Ap-
proximation error can be reduced by increasing the
number of fuzzy rules. However, in order to decrease
the size of the fuzzy rules, we use the sliding surface
σ(t) instead of X as the input of the fuzzy logic sys-
tem. Simulation shows that this produces reasonable
results compared to using X.
3.2 Fault Accommodation Scheme
3.2.1 Normal Controller
The general chattering-free sliding mode control law
with the saturation function is given by
v(t) = −ksat(σ/ε), (15)
where ε is a small positive constant.
The 2nd SMC fault tolerant control design of the
authors in reference (Li et al., 2010) is proposed as:
v(t) = −k
1
σ(t) − k
2
Z
t
0
σ(t)dt (16)
With this chattering-free2nd SMC law, the system
enters a vicinity of the 2nd-SM σ(t) =
˙
σ(t) = 0 and
then to a vicinity of the origin, locally and asymptoti-
cally.
We then apply the 2nd order sliding mode control
for satellite formation flying. Rewrite the nonlinear
dynamics model of formation flying (equation 1) as
f(t, X,u) = AX + E(X). The new 2nd sliding mode
controller is written as
u
n
(t) = −k
1
σ(t)−k
2
Z
t
0
σ(t)dt −C
g
[AX +E(X)−
¨
Xd]
(17)
where C
g
=


2 0 0 1 0 0
0 2 0 0 1 0
0 0 2 0 0 1


.
3.2.2 Accommodation Control of System failures
After fault isolation, the fault tolerant 2nd SMC law
with fuzzy identifier is designed as
u = u
n
+ u
f
(18)
Rewrite the term ˆg(t, X,u | θ
g
) in equation 14 as
ˆg
r
(t, σ,u | θ
g
). ˆg
r
(t, σ,u | θ
g
) = θ
T
g
ξ
g
(t, σ,u), where
˙
θ
g
= ασξ
g
. The controller to accommodate the fault
is u
f
= θ
T
g
ξ
g
(t, σ,u).
4 RESULTS AND DISCUSSION
The desired formation considered for ideal forma-
tion keeping is a projected circular formation. The
phase angle (φ) between the leader and follower satel-
lite is assumed to be zero. The initial states for the nu-
merical simulation are computed by substituting t = 0
and adding a 1 km position offset on x, y, and z. All
simulation cases are assumed to run 4 orbits. The SFF
system parameters and the orbital parameters for the
leader satellite used in the numerical simulations are
given in Table 1.
4.1 Constant Fault Case
We use the thruster constant additive fault scenario in
this study as: T
ti
=

0 t < t
f
5× 10
−1
N t ≥ t
f
Periodic additive fault is assumed to be perma-
nently added to all thrusters after 0.5 orbits. The
INTELLIGENT FAULT DETECTION, IDENTIFICATION AND CONTROL OF SATELLITE FORMATION FLYING
87

Table 1: Satellite Parameters.
Parameter Value
m
F
(kg) 1
µ
e
(km
3
s
−2
) 398600
r
L
(km) 6878
e 0.1
i (deg) 45
φ (deg) 0
Ω, ω, i, M (deg) 0
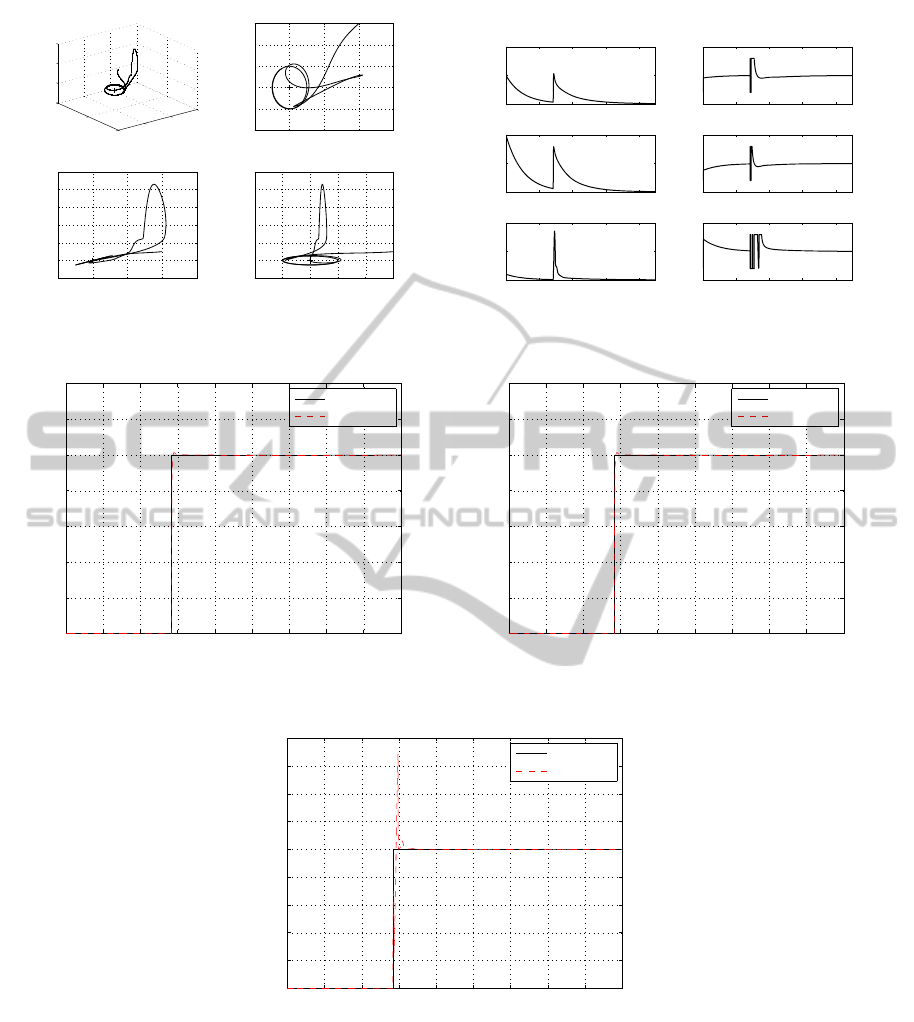
3D trajectory with fault detection, isolation and ac-
commodation is shown in Figure 2(a). The forma-
tion keeping is still available after the fault using the
fault tolerant 2nd SMC law. Figure 2(b) shows rel-
ative position errors and control demand for forma-
tion keeping. The steady-state errors on the radial,
along track, and cross track directions are bounded by
3m. Then, we use the proposed second sliding mode
observer with fuzzy identifier for fault detection and
isolation. The threshold
˜
X
M
is assumed as 100m/s
2
.
The faults T
ti
(i=1,2,3) and fault isolation results
ˆ
T
ti
(i=1,2,3) are given in Figures 2(c), 2(d) and 2(e). The
fault added on the actuator of the radial, along track,
and cross track directions are isolated using the fuzzy
logic identifier.
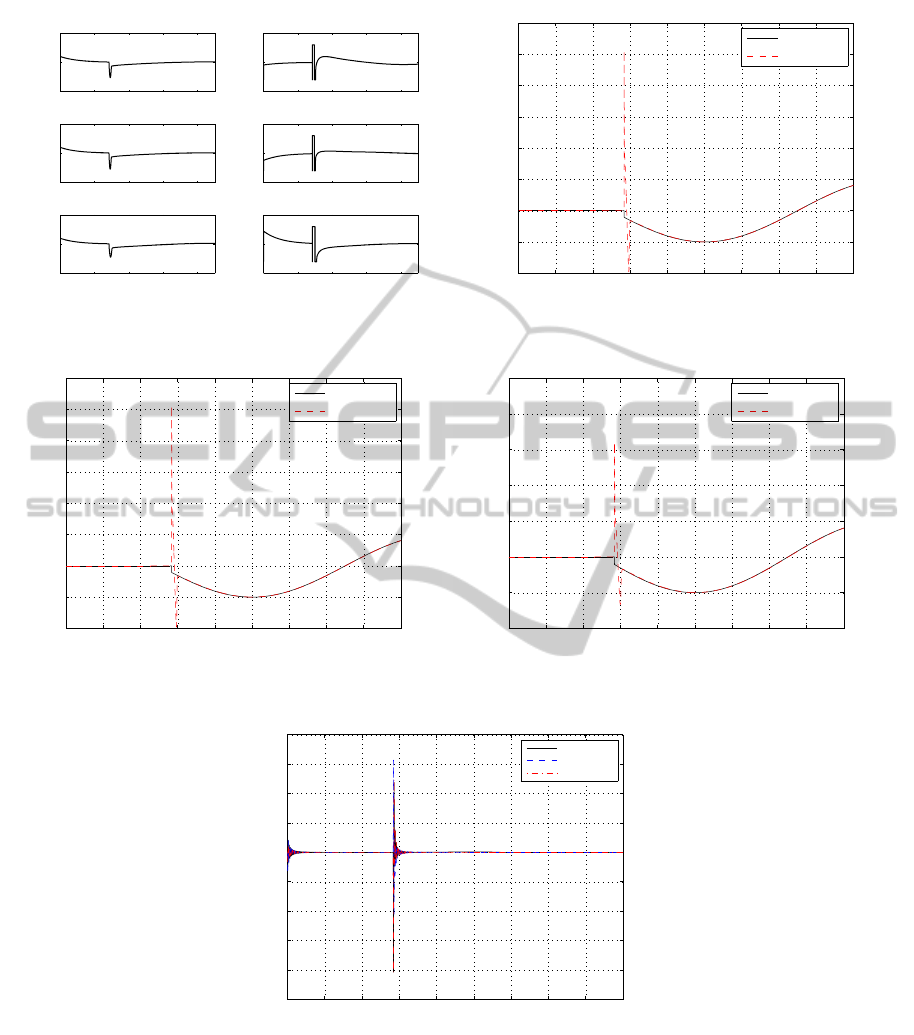
4.2 Time-varying Fault Case
In order to test the robustness for other faults, we use
the time-varying additive fault scenario in this study
as:
T
ti
=

0 t < t
f
5× 10
−2
× cos(2× 10
−4
3.14159t)N t ≥ t
f
Figure 3(a) shows relative position errors and con-
trol demand for formation keeping. The steady-state
errors on the radial, along track, and cross track direc-
tions are bounded by 80m. The faults T
ti
(i=1,2,3) and
fault isolation results
ˆ
T
ti
are givenin Figures 3(b), 3(c)
and 3(d). The residuals are shown in Figure 3(e). The
fault detection and isolation results are as good as that
of the constant fault case. The fault accommodation
control results for time-varying faults are reasonable.
5 CONCLUSIONS
This paper presents an analysis of satellite formation
keeping using a fault diagnosis and control scheme
based on a second order sliding mode observer, fuzzy
identifier and second order sliding mode controller.
The thruster faults considered are modeled as con-
stant and time varying additive faults which occur at
unknown times. Results of numerical simulation in-
dicate that the proposed FDI and fault tolerant control
methodology can force the formation keeping error
to converge to a small neighborhood near zero (less
than 3m under constant case and less than 80m under
time varying fault). Moreover, the numerical results
clearly establish the robustness of the proposed fault
detection, identification and control methodologies in
tracking a desired formation even in the presence of
thruster faults as well as time-varying disturbances.
REFERENCES
Azizi, S. M. and Khorasani, K. (2008). Cooperative
fault accommodation in formaiton flying satellites.
Proceedings of American Control Conference, page
WrB01.4.
Benosman, M. (2010). A survey of some recent results on
nonlinear fault tolerant control. Mathematical Prob-
lems in Engineering, pages 1 – 15.
Davila, J., Fridman, L., and Levant, A. (2005). Second-
order sliding mode observer for mechanical sys-
tems. IEEE Transactions on Automatic Control,
50(11):1785 – 1789.
Edwards, C., Fridman, L., and Thein, M.-W. L. (2007).
Fault reconstruction in a leader/follower spacecraft
system using higher order sliding mode observers.
Proceedings of American Control Conference, page
WeA13.1.
Li, J., Pan, Y. D., and Kumar, K. D. (2010). Formation
flying control of small satellites. In Proc. of the 2010
AIAA Guidance, Navigation, and Control Conference,
volume AIAA-2010-8296, Toronto, Ontario.
Valdes, A. and Khorasani, K. (2010). A pulsed plasma
thruster fault detection and isolation strategy for for-
mation flying of satellites. Applied Soft Computing,
pages 746 – 758.
Wang, L. (1997). A Course in Fuzzy Systems and Control.
Prentice-Hall, New York, NJ.
Wong, H., Kapila, V., and Sparks, A. G. (2002). Adaptive
output feedback tracking control of spacecraft forma-
tion. International Journal of Robust and Nonlinear
Control, 12(2-3):117 – 139.
Wu, Q. and Saif, M. (2007). Robust fault detection and
diagnosis for a multiple satellite formation flying sys-
tem using second order sliding mode and wavelet net-
works. Proceedings of American Control Conference,
page WeA13.4.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
88

−1000
0
1000
2000
−2000
0
2000
−5000
0
5000
10000
x [m]
y [m]
z [m]
−500 0 500 1000 1500
−1000
−500
0
500
1000
1500
x [m]
y [m]
−500 0 500 1000 1500
−2000
0
2000
4000
6000
8000
10000
x [m]
z [m]
−1000 −500 0 500 1000 1500
−2000
0
2000
4000
6000
8000
10000
y [m]
z [m]
(a) 3D Trajectory with FTC
0 2000 4000 6000 8000
0
1000
2000
e
x
[m]
0 2000 4000 6000 8000
0
500
1000
e
y
[m]
0 2000 4000 6000 8000
0
5000
10000
time [s]
e
z
[m]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
u
x
[m/s
2
]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
u
y
[m/s
2
]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
time [s]
u
z
[m/s
2
]
(b) Relative Position Errors and Control Input
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Fault Isolation of Along Track Direction
time [s]
Fault [km/s
2
]
T
t1
T
t1
Estimation
(c) Constant Thruster Fault Isolation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Fault Isolation of Radial Direction
time [s]
Fault [km/s
2
]
T
t2
T
t2
Estimation
(d) Constant Thruster Fault Isolation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Fault Isolation of Cross Track Direction
time [s]
Fault [km/s
2
]
T
t3
T
t3
Estimation
(e) Constant Thruster Fault Isolation
Figure 2: Fault Tolerant Control and Fault Isolation Simulation under Constant Thruster Fault.
INTELLIGENT FAULT DETECTION, IDENTIFICATION AND CONTROL OF SATELLITE FORMATION FLYING
89

0 2000 4000 6000 8000
−5000
0
5000
e
x
[m]
0 2000 4000 6000 8000
−5000
0
5000
e
y
[m]
0 2000 4000 6000 8000
−5000
0
5000
time [s]
e
z
[m]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
u
x
[m/s
2
]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
u
y
[m/s
2
]
0 2000 4000 6000 8000
−5
0
5
x 10
−3
time [s]
u
z
[m/s
2
]
(a) Relative Position Errors and Control Input
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
−0.1
−0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
Fault Isolation of Along Track Direction
time [s]
Fault [km/s
2
]
T
t1
T
t1
Estimation
(b) Time Varying Thruster Fault Isolation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
−0.1
−0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
Fault Isolation of Radial Direction
time [s]
Fault [km/s
2
]
T
t2
T
t2
Estimation
(c) Time Varying Thruster Fault Isolation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
−0.1
−0.05
0
0.05
0.1
0.15
0.2
0.25
Fault Isolation of Cross Track Direction
time [s]
Fault [km/s
2
]
T
t3
T
t3
Estimation
(d) Time Varying Thruster Fault Isolation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
−25
−20
−15
−10
−5
0
5
10
15
20
Fault Detection
time [s]
Residual
Along Track
Radial
Cross Track
(e) Residual of Fault Detection by 2nd SM Observer
Figure 3: Fault Tolerant Control and Fault Isolation Simulation under Time Varying Thruster Fault.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
90