PATH OPTIMIZATION FOR HUMANOID WALK PLANNING
An Efficient Approach
Antonio El Khoury, Michel Ta¨ıx and Florent Lamiraux
CNRS, LAAS, 7 avenue du colonel Roche, F-31077 Toulouse Cedex 4, France
Universit´e de Toulouse, UPS, INSA, INP, ISAE, UT1, UTM, LAAS, F-31077 Toulouse Cedex 4, France
Keywords:
Humanoid robot, Motion planning, Walk planning, Holonomic constraints, Optimization, A*, HRP-2.
Abstract:
This paper deals with humanoid walk planning in cluttered environments. It presents a heuristic and efficient
optimization method that takes as input a path computed for the robot bounding box, and produces a path
where a discrete set of configurations is reoriented using an A* search algorithm. The resulting trajectory is
realistic and time-optimal. This method is validated in various scenarios on the humanoid robot HRP-2.
1 RELATED WORK AND
CONTRIBUTION
The problem of humanoid walk planning can be
defined as follows: given an environment and a
humanoid robot with start and goal placements, a
collision-free trajectory needs to be found. It should
ideally represent realistic human motion, i.e. a mo-
tion similar to that of a human being in the same con-
ditions. This result is desirable since humanoid robots
are bound to movein man-made environmentssuch as
homes, offices, and factories and because it can help
them blend in among humans.
1.1 Humanoid Walk Planning
The problem of motion planning is now well formal-
ized in robotics and several books present the vari-
ous approaches (Latombe, 1991; Choset et al., 2005;
LaValle, 2006). Sampling-based methods rely on ran-
dom sampling in the configuration space (CS) and use
for instance Probabilistic Roadmaps (PRM) (Kavraki
et al., 1996) or Rapidly-Expanding Random Trees
(RRT) (Kuffner and LaValle, 2000). With these meth-
ods it is possible to solve problems for systems with
large numbers of Degrees of Freedom (DoF).
The motion planning problem is certainly a com-
plex one in the case of humanoid robots, which
are high-DoF redundant systems that have to verify
bipedal stability constraints. Various planning strate-
gies can be found in literature.
One category relies on whole-body task planning:
Figure 1: Humanoid Robot HRP-2 uses holonomic motion,
or side-stepping, to pass between two chairs.
kinematic redundancy is used to accomplish tasks
with different orders of priorities (Khatib et al., 2004;
Kanoun et al., 2009). Static balance and obstacle
avoidance can thus be defined as tasks that the algo-
rithm has to respect.
Works of (Kuffner et al., 2001; Chestnutt et al.,
2005) describe in particular humanoid footstep plan-
ning schemes. Starting from an initial footstep place-
ment, they use an A* graph search (Hart et al., 1968)
to explore a discrete set of footstep transitions. The
search stops when the neighborhood of the goal foot-
step placement is reached. This approach is not prac-
tical in some environments with narrow passages, and
(Xia et al., 2009) reduced the computational cost of
footstep planning by using an RRT planning algo-
rithm.
Another strategy consists of dividing a high-
dimensional problem into smaller problems and solv-
179
El Khoury A., Taïx M. and Lamiraux F..
PATH OPTIMIZATION FOR HUMANOID WALK PLANNING - An Efficient Approach.
DOI: 10.5220/0003530001790184
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 179-184
ISBN: 978-989-8425-75-1
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ing them successively (Zhang et al., 2009). The idea
of dividing the problem into a two-stage scheme is de-
scribed in (Yoshida et al., 2008): A 36-DoF humanoid
robot is reduced to a 3-DoF bounding box. Using the
robot simplified model, the PRM algorithm solves the
path planning problem and generates a feasible path
for the bounding box. A geometric decomposition of
the path places footsteps on it, and a walk pattern gen-
erator based on (Kajita et al., 2003) finally produces
the whole-body trajectory for the robot. In (Moulard
et al., 2010), this two-stage approach is also used; nu-
merical optimization of the bounding box path pro-
duces a time-optimal trajectory that is constrained by
foot speed and distance to obstacles.
Another important issue is the notion of holo-
nomic motion: while wheeled robots always remain
tangent to their path, thus following a nonholonomic
constraint, legged robots can also move sideways, and
their motion can be described as holonomic. The path
planning scheme in (Yoshida et al., 2008) is designed
to this end; a PRM algorithm first builds a roadmap
with Dubins curves (Dubins, 1957); but such curves
impose a nonholonomic constraint and narrow pas-
sages cannot be crossed. The roadmap is therefore
enriched with linear local paths. As a result this plan-
ning scheme generates motion such that the robot re-
mains tangent to its path most of the time and uses
sidestepping only in narrow passages.
Furthermore, (Mombaur et al., 2010) conducted
a series of walking experiments that allowed them to
build a model of human walking trajectories; if a hu-
man being walks long distances, his body tends to
be tangential to his path, while holonomic motion is
used over smaller distances. This is an attractive prop-
erty for computed paths if a realistic motion is to be
achieved, and holonomic motion can as well be used
to pass through narrow spaces. These results suggests
that a good combination of both nonholonomic and
holonomic motions can be used to achieve realistic
walking.
1.2 Contribution
The work of (Moulard et al., 2010) solves the walk
planning problem in a natural way, i.e. it uses numer-
ical optimization to minimize the robot walking along
the path while following speed and obstacle distance
constraints. After having tried this approach, it was
empirically concluded that achieving successful nu-
merical optimization in any kind of environment is a
difficult and computationally expensive task; in fact,
it requires computing a large set of parameters to fully
define the optimized path.
While using the same two-stage approach of
(Yoshida et al., 2008), a simpler heuristic method that
generates realistic time-optimal humanoid trajectories
is proposed. First the PRM algorithm and the Dubins
local paths are replaced with an RRT-Connect algo-
rithm and linear local paths. The path is then opti-
mized by locally reorienting the robot bounding box
on a discrete set of configurations of the path. Priority
to nonholonomicmotion is considered and holonomic
motion is used only to pass in narrow passages and to
avoid nearby obstacles.
The following section presents this method and
explains how it is integrated in the motion planning
scheme. Examples of different scenarios, including a
real one with the HRP-2 platform, are shown in Sec-
tion 3.
2 OPTIMIZATION BY REGULAR
SAMPLING
Assuming full knowledge of the environment, the
RRT algorithm produces a collision-free piecewise
linear path P
RRT
for the robot bounding box (in offline
mode), i.e. the path consists of the concatenation of
linear local paths LP
RRT
.
Due to the probabilistic nature of RRTs, P
RRT
may
not be optimal in terms of length, and a preliminary
random shortcut optimization (RO) can be run in or-
der to shorten it (See Figure 2). While the optimized
path P is collision-free, the bounding box orientation
is such that it could lead to an unrealistic trajectory
that is not time-optimal. For instance, the humanoid
robot could spend a long time walking sideways or
backwards over a long distance in an open space. An
additional optimization stage is introduced to address
this issue in the next section.
2.1 Bounding Box Path Optimization
Note that each configuration q can be written as q =
(X, θ), where X = (x, y) describes the bounding box
position in the horizontal plane, and θ gives its ori-
entation. The optimizer reorients the bounding box
along P by changing θ while retaining the value of X.
For this purpose, an A* search algorithm is exe-
cuted; first P is regularly sampled. Using a discrete
set of possible orientations for each sample configu-
ration and an adequate heuristic estimation function,
the bounding box orientation is then modified along
P. An optimized path P
opt
is created and leads to a
realistic time-optimal trajectory.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
180

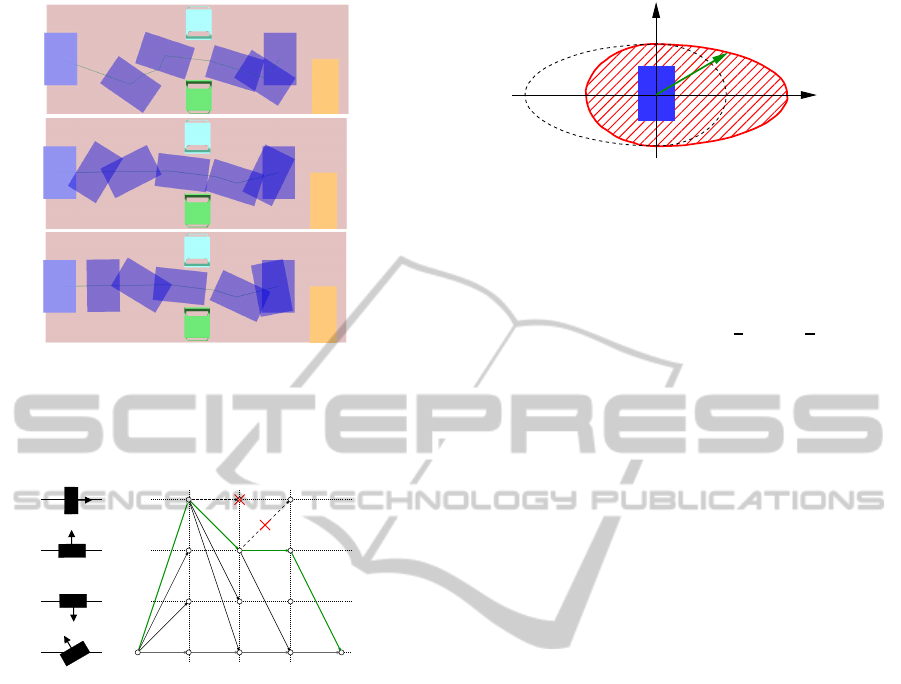
(a)
(c)
(b)
Figure 2: Top view: (a) RRT-Connect path for the bound-
ing box passing between two chairs. (b) Optimized bound-
ing box path by random optimization (RO). (c) Optimized
bounding box after adding regular sampling optimization
(RSO).
P
opt
G
P
q
g
q
s
lat
2
lat
1
front
init
n n+1
Figure 3: Each initial sample configuration can be rotated
and be in one of four states. Starting from q
s
, the A*
search algorithm searches the graph G that contains only
valid nodes and arcs to produce an optimized path P
opt
.
2.1.1 Preliminary Notations
After running RO on the piecewise linear path P
RRT
,
the path P is also piecewise linear, and its first and last
configurations are denoted by q
s
and q
g
.
Let d
sample
∈ R
∗
+
be a sampling distance. Sam-
pling P with a distance d
sample
means dividing each
local path LP
j
of P into smaller local paths of length
d
sample
; each new local path end is a sample configu-
ration. The n
th
sample configuration of P in its intial
state can be obtained by indexing new local path ends
starting from q
s
, and is denoted by q
init
n
.
The possible orientation states need to be defined.
We aim to make a humanoid robot reach its goal as
soon as possible. Since the robot is faster while walk-
ing straight than side-stepping, we attempt to change
the orientation of each inital sample configuration q
init
n
such that the bounding box is tangent to the local path
and introduce a new configuration denoted by q
front
n
.
v
f
v
lat
v
max
lat
v
max
f
v
min
f
−
C
v
Figure 4: The rectangular bounding box speed vector v is
bounded inside the hashed area defined by the speed con-
straint C. The area is bounded by the union of two half-
ellipsoids.
To take into account the fact that there may be obsta-
cles that forbid a frontal orientation, we also create
q
lat
1
n
and q
lat
2
n
that are rotated by
π
2
and −
π
2
relative
to the path tangent, see Figure 3. One particular case
is local path end configurations: the mean direction
of the two adjacent local paths is considered to de-
fine frontal and lateral configurations. This is done to
ensure a smooth transition between two local paths.
A sample configuration whose orientation is un-
known will be denoted by q
state
n
. It can have any ori-
entation state of the set {init, front, lat
1
, lat
2
} ex-
cept for q
s
and q
g
which remain in their initial state.
Ideally, the algorithm should be able (as long as there
are no obstacles) to put each sample configuration in
the frontal state, create a new path P
opt
and generate a
time-optimal trajectory for the robot.
An A* search is run to achieve this goal; the algo-
rithm functions are described in the following section.
2.1.2 A* Function Definition
An A* search algorithm can find an optimal path in
a graph as long as a graph and an evaluation function
are correctly defined. Starting from q
s
, A* expands in
each iteration the possible transitions from one sam-
ple to the next one in the graph and evaluates with
the evaluation function the cost of going through each
different state, see Figure 3.
A graph G is defined to be a set of nodes and arcs.
A valid node q
state
n
n
is defined to be a configuration
with no collisions, and a valid arc q
state
n
n
q
state
n+1
n+1
is a
collision-free local path. The whole graph G could
be built before running A* by testing all nodes and
arcs and making sure they are collision-free. But col-
lision tests are slow, and A* uses a heuristic estima-
tion function to avoid going through all nodes. An
empty graph G is thus initialized and nodes and arcs
are built only when necessary. A successor operator
needs to be defined for this purpose.
The Successor Operator Γ(q
state
n
n
). Its value for
any node q
state
n
n
is a set {(q
state
n+1
n+1
, c
n,n+1
)}, where
PATH OPTIMIZATION FOR HUMANOID WALK PLANNING - An Efficient Approach
181

q
state
n+1
n+1
denotes a successor node, and c
n,n+1
is the
cost of going from q
state
n
n
to q
state
n+1
n+1
. The cost c
n,n+1
is defined to be the distance D(q
state
n
n
, q
state
n+1
n+1
) be-
tween two nodes of G; it computes the walk time from
q
state
n
n
to q
state
n+1
n+1
. The speed constraint C is defined
as:
C =







(
v
f
v
f
max
)
2
+ (
v
lat
v
lat
max
)
2
− 1 if v
f
>= 0
(
v
f
v
f
min
)
2
+ (
v
lat
v
lat
max
)
2
− 1 if v
f
< 0
(1)
where v
f
and v
lat
are respectively the frontal and lat-
eral speed, and v
f
min
v
f
max
and v
lat
max
their minimum and
maximum values (See Figure 4).D(q
state
n
n
, q
state
n+1
n+1
)
can be then computed by integrating this speed con-
straint along it.
Having expressed the successor operator, which
allows the optimizer to choose wich node to expand
at each iteration, the A* evaluation function can be
defined.
The Evaluation Function
ˆ
f(q
state
n
). It is the esti-
mated cost of an optimal path going through q
state
n
from q
s
to q
g
and can be written as:
ˆ
f(q
state
n
) = ˆg(q
state
n
) +
ˆ
h(q
state
n
) (2)
where ˆg(q
state
n
) is the estimated cost of the optimal
path from q
s
to q
state
n
and
ˆ
h(q
state
n
) is a heuristic func-
tion giving the estimated cost of the optimal path from
q
state
n
to q
g
.
ˆ
h(q
state
n
) must verify
ˆ
h(q
state
n
) ≤ h(q
state
n
) to ensure
that the algorithm is admissible, i.e. the path from
q
s
to q
g
is optimal. Since the robot is fastest while
walking straight forward in the absence of obstacles,
ˆ
h(q
state
n
) is defined as:
ˆ
h(q
state
n
) = D(q
state
n
, q
front
n+1
)
+
N
sample
−n−2
∑
k=1
D(q
front
n+k
, q
front
n+k+1
)
+ D(q
front
n+1
, q
g
)
(3)
where N
sample
is the total number of initial sample
configurations in P including q
s
and q
g
.
ˆ
h(q
state
n
) thus
sums the cost of walking along P while staying tan-
gential to the path with the start and end transition
costs from q
state
n
and to q
g
.
Now that the A* functions are fully defined, a
search algorithm can be run to compute an optimal
path P
opt
by changing the orientation of each sample
node. An example is shown in Figure 5.
2.2 Motion Generation for a Humanoid
Robot
A collision-free path P for the 3-DoF bounding box
can be found using RRT-Connect and RO. The regular
sampling optimization (RSO), which is the subject of
this paper, is then applied on the path and produces a
path P
opt
that gives priority to nonholonomic motion.
Once the bounding box trajectory is computed, the
robot has to walk along it. A footstep sequence is thus
generated along P
opt
by geometric decomposition of
the path, and the pattern generator cited in subsection
1.1 then produces the robot whole-body trajectory.
3 EXAMPLES
This section presents experimental results of the path
optimizer after it has been inserted in the previously
described walk planning scheme. Distance parame-
ters v
f
max
, v
lat
max
, v
f
min
are set to 0.5, 0.1, and 0.25 re-
spectively. d
sample
is equal to
h
6
, where h is the hu-
manoid’s height. Tests are performed on a 2.13 GHz
Intel Core 2 Duo PC with 2 GB RAM. Simulations
d
sample
O
2
1
O
q
s
q
n+1
front
q
n
lat
1
q
n
init
q
n+1
init
Figure 5: Local paths are regularly sampled (light grey) and
each sample configuration is reoriented (dark) while con-
sidering obstacles O
1
and O
2
.
of the humanoid robot HRP-2 are run in three scenar-
ios. The first one is a small environmentwhere HRP-2
has to pass between two chairs. The second environ-
ment is uncluttered with few obstacles lying around,
while the last one is a bigger apartment environment
where the robot has to move from one room to an-
other while passing through doors. The chairs sce-
nario motion is also replayed on the real robot HRP-2
(See Figure 1). Videos for all scenarios can be viewed
at http://humanoid-walk-planning.blogspot.com/.
Table 1 shows computation times for each stage
of the planning scheme: RRT-Connect, RO, RSO, and
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
182

Table 1: Columns 1 to 5: Computational time (ms) of each planning stage for the presented scenarios. Columns 6 and 7:
Humanoid robot walk time (s) for the presented scenarios using RO alone and a RO-RSO combination.
RRT-Connect RO RSO Robot Trajectory Total RO RO+RSO
Chairs 3, 968 1, 887 2, 144 66, 140 74, 140 40 35
Galton 91.69 2, 497 237.8 65, 730 68, 560 66 57
Apartment 1, 212 2, 425 2, 412 222, 800 228, 800 200 120
Figure 6: Perspective view of the simulated HRP-2 trajec-
tory on the final optimized path passing between two chairs.
the whole-body robot trajectory generation. In order
to show the optimizer contribution, robot walk times
are also measured by creating a trajectory directly af-
ter RO, and comparing it with a trajectory where the
RSO was added.
3.1 “Chairs” Scenario
Figure 2 shows the bounding box RRT path and the
RO path for the chairs scenario. It is obvious that RO
creates a shorter path, but the bounding box starts ro-
tating from the beginning of the path even though the
two chairs are still far. This causes the robot trajec-
tory to be unrealistic on one hand and, since walking
sideways takes a longer time than walking straight, to
also not be time-optimal.
Figure 7: Perspective view of HRP-2 optimized trajectory
in the Galton board scenario.
However, after applying RSO, it is clear that the
bounding box stays oriented towards the front and ro-
tates only when it reaches the chairs. Figure 6 and
Figure 1 show that the walk time is shorter by 5 s and
Figure 8: Perspective view of HRP-2 optimized trajectory
in the apartment scenario.
the final trajectory for HRP-2 is more realistic. Note
that the RSO takes 2,144 ms to be executed on the
chairs path, which is less than 3% of the total compu-
tation time.
3.2 “Galton” Scenario
An uncluttered environment is considered in this case,
and it can be seen that RRT-Connect and RSO compu-
tation times are very low compared to other environ-
ments. This can be explained by the fact that a tree
connecting start and goal configurations is easier to
find, and that the frontal orientation state is valid for
all considered samples on the path (See Figure 7).
3.3 “Apartment” Scenario
The planning scheme is finally applied in the apart-
ment scenario. In Figure 8, it is evident that HRP-2
walks facing forward through the doors. As with pre-
vious scenarios, the trajectory is more realistic than a
trajectory where RSO is not used. The added compu-
tation time for RSO is 2,412 ms, which is insignificant
compared to the 228 s it takes for the whole planning
scheme.
Additionally, since the environment is signifi-
cantly larger and more constrained than the previous
ones, the walk time difference is more striking: Table
1 shows that it takes the robot 80 s less to cross the
apartment when an RO-RSO combination is used.
PATH OPTIMIZATION FOR HUMANOID WALK PLANNING - An Efficient Approach
183

4 CONCLUSIONS
In this paper, a novel simple optimization method is
presented for humanoid walk planning that relies on a
decoupling between trajectory and robot orientations.
It uses an A* search that takes as input a path for
the robot bounding box, and produces a path where
a discrete set of configurations have been reoriented
to generate a realistic time-optimal walk trajectory.
Results show that new trajectories are more satisfac-
tory while the added computation time is insignificant
compared to the whole planning time.
Of course, this approach can be used in other fields
such as graphical animation for digital actors to adapt
the body orientation with respect to the goal during
locomotion. With a motion capture library containing
pre-recorded nonholonomic and holonomic walk be-
haviors, it is possible to lay this behavior on the actor
trajectory and produce realistic movements.
ACKNOWLEDGEMENTS
This work was supported by the French FUI Project
ROMEO.
REFERENCES
Chestnutt, J., Lau, M., Cheung, G., Kuffner, J., Hodgins,
J., and Kanade, T. (2005). Footstep planning for the
honda asimo humanoid. In Robotics and Automation,
2005. ICRA 2005. Proceedings of the 2005 IEEE In-
ternational Conference on, pages 629 – 634.
Choset, H., Lynch, K. M., Hutchinson, S., Kantor, G. A.,
Burgard, W., Kavraki, L. E., and Thrun, S. (2005).
Principles of Robot Motion: Theory, Algorithms, and
Implementations. MIT Press, Cambridge, MA.
Dubins, L. E. (1957). On curves of minimal length with a
constraint on average curvature, and with prescribed
initial and terminal positions and tangents. American
Journal of Mathematics, 79(3):pp. 497–516.
Hart, P., Nilsson, N., and Raphael, B. (1968). A Formal Ba-
sis for the Heuristic Determination of Minimum Cost
Paths. IEEE Transactions on Systems Science and Cy-
bernetics, 4(2):100–107.
Kajita, S., Kanehiro, F., Kaneko, K., Fujiwara, K., Harada,
K., Yokoi, K., and Hirukawa, H. (2003). Biped
walking pattern generation by using preview control
of zero-moment point. In Robotics and Automa-
tion, 2003. Proceedings. ICRA ’03. IEEE Interna-
tional Conference on, volume 2.
Kanoun, O., Lamiraux, F., Wieber, P.-B., Kanehiro, F.,
Yoshida, E., and Laumond, J.-P. (2009). Prioritiz-
ing linear equality and inequality systems: Applica-
tion to local motion planning for redundant robots. In
Robotics and Automation, 2009. ICRA ’09. IEEE In-
ternational Conference on, pages 2939 –2944.
Kavraki, L., Svestka, P., Latombe, J.-C., and Overmars, M.
(1996). Probabilistic roadmaps for path planning in
high-dimensional configuration spaces. Robotics and
Automation, IEEE Transactions on, 12(4):566 –580.
Khatib, O., Sentis, L., Park, J., and Warren, J. (2004).
Whole-body dynamic behavior and control of human-
like robots. Int. J. Humanoid Robotics, 1(1):29–43.
Kuffner, J.J., J. and LaValle, S. (2000). Rrt-connect: An
efficient approach to single-query path planning. In
Robotics and Automation, 2000. Proceedings. ICRA
’00. IEEE International Conference on, volume 2,
pages 995 –1001 vol.2.
Kuffner, J.J., J., Nishiwaki, K., Kagami, S., Inaba, M.,
and Inoue, H. (2001). Footstep planning among ob-
stacles for biped robots. In Intelligent Robots and
Systems, 2001. Proceedings. 2001 IEEE/RSJ Interna-
tional Conference on, volume 1, pages 500 –505 vol.1.
Latombe, J.-C. (1991). Robot Motion Planning. Kluwer
Academic Publishers, Norwell, MA, USA.
LaValle, S. M. (2006). Planning Algorithms. Cambridge
University Press, Cambridge, U.K.
Mombaur, K., Truong, A., and Laumond, J.-P. (2010). From
human to humanoid locomotion–an inverse optimal
control approach. Auton. Robots, 28:369–383.
Moulard, T., Lamiraux, F., and Wieber, P.-B. (2010).
Collision-free walk planning for humanoid robots
using numerical optimization. Retrieved from
http://hal.archives-ouvertes.fr/hal-00486997/en/.
Xia, Z., Chen, G., Xiong, J., Zhao, Q., and Chen, K.
(2009). A random sampling-based approach to goal-
directed footstep planning for humanoid robots. In
Advanced Intelligent Mechatronics, 2009. AIM 2009.
IEEE/ASME International Conference on.
Yoshida, E., Esteves, C., Belousov, I., Laumond, J.-P.,
Sakaguchi, T., and Yokoi, K. (2008). Planning 3-
d collision-free dynamic robotic motion through it-
erative reshaping. Robotics, IEEE Transactions on,
24(5):1186 –1198.
Zhang, L., Pan, J., and Manocha, D. (2009). Motion plan-
ning of human-like robots using constrained coordi-
nation. In Humanoid Robots, 2009. Humanoids 2009.
9th IEEE-RAS International Conference on.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
184