APPLICATION OF INTERNAL MODEL CONTROLLER FOR

WIND TURBINE SYSTEM CONSIDERING TIME-DELAY

ELEMENT

Faramarz Asharif, Shiro Tamaki, Tstomu Nagado

Faculty of Engineering, Ryukyu University, Okinawa, Japan

Nagata Tomokazu, Mohammad Reza Alsharif

Faculty of Engineering, Ryukyu University, Okinawa, Japan

Keywords: Internal Model Controller, Tele-Operation, H

norm, MIMO System, Wind Turbine.

Abstract: In this paper, we aim to modify the system which includes time-delay elements including closed loop system

and uncertainty of the wind turbine system and time-delay elements. Time-delay will happen during the long

distance communication. By observing and controlling the attitude of wind turbine system from distance, the

transmitted control input and output signal will be delayed certainly. For this reason even thought wind

turbine system is a stable system, but it will be an unstable system by time-delay elements. So, here we

consider about the IMC method which is one of the robust controllers. IMC method is composed of optimum

controller and uncertainty model of control object and time-delay elements. The optimum controller is

norm in order to

stabilize the closed loop system considering the uncertainty of control object and predicted time-delay

element and at the same time minimize the effects of time-delay element in sensitivity function. In this

research controlling of the angular velocity and pitch angle of bale is considered. In order to have a stable

angular velocity, we implied Internal Model Controller. As consequences, angular velocity converges to

reference signal with good performance.

1 INTRODUCTION

In this research, we propose control of the time-

delay system by using IMC (Internal Model

Controller).There were many schemes and

suggestions to consider about the designing

controller for systems which including time-delay

elements. For example the classical way is PID

controller (Proportional, Integral Derivative).

However, this scheme is not suitable for large time-

delay. On the other hand, LQI (Linear Quadratic

Integration) method which is modern way and it

warranties the stability even for a large time-delay.

However, for MIMO system, it is very difficult to

construct a suitable controller due to existence of

time-delay elements. Therefore, we consider IMC

method to control the system including time-delay

elements. Time-delay will happen during utilization

of the long distance communication. The application

of the long distance communication is an important

issue in aerospace engineering. When we have a

control object in the long distance, the transmitter’s

signal will be delay. Therefore the received signal at

The control object will also be delayed. Moreover,

the feedback signal to transmitter location will also

be delayed. So, in this case, we have a round trip

delay, one delay is to reach the control object and

another delay is to receive the feedback signal for

comparison with the reference signal. This

comparison makes the error signal of the control

system. This error must be decreased for a better

controlling system. Moreover, control object will be

unstable due to time-delay elements. Therefore, in

this paper we consider the stability of control object

and its uncertainty. Also, not only the uncertainty of

control object, but also the uncertainty of time-delay

elements which is estimated and approximated by

using Pade approximation has been considered. IMC

method is minimizing the coefficient of external

disturbance of output signal by H

norm. Therefore,

by this design problems of the system instability,

199

Asharif F., Tamaki S., Nagado T., Tomokazu N. and Reza Alsharif M..

APPLICATION OF INTERNAL MODEL CONTROLLER FOR WIND TURBINE SYSTEM CONSIDERING TIME-DELAY ELEMENT.

DOI: 10.5220/0003531601990202

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 199-202

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

uncertainty and external disturbance have been

overcomes. Then, it can be solved by one of the

robust controller such as IMC method.

2 THE BASIC THEORY OF

TIME-DELAY SYSTEM AND

BACK GORUND OF

RESEARCH

As we express in introduction in this research, we

have a round trip time-delay system which means

one delay element to reach the control object and

another delay element to feedback the output signal

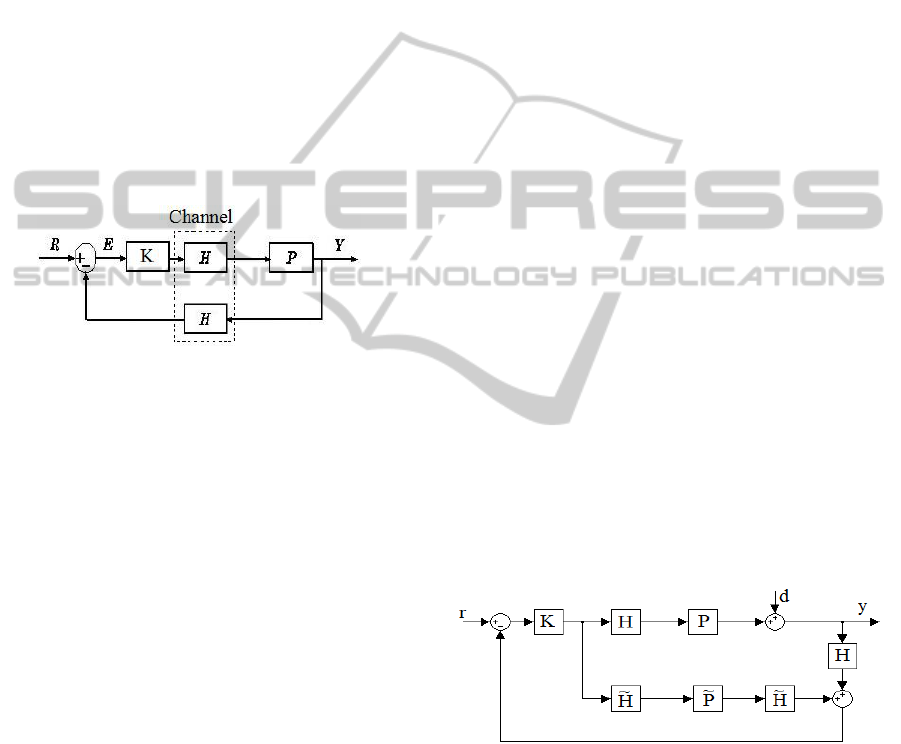
in order to compare with reference signal. Figure.1

shows the block diagram of a round trip time-delay

system without controller.

Figure 1: Conventional feedback control.

Here “Y”,”H”,”R”,”P” and “E” are the output

signal of the system, time-delay element, reference

signal, control object and error signal of the system,

respectively. Through figure 1 it is clear that the

sensitivity (S) and transfer function (T) are obtained

as follows:

)

( PKHIS +=

(1)

PKHPKHIT

)

(

−

(2)

Generally, in feedback control system, by

adding some controller such as “K” which is

designed corresponding to control object, we can

minimize the error signal. Therefore, in classical

control usually PID controller and in modern control

integrator operation and optimum gain such as LQI

method are used. But, minimizing the error signal of

the system is not enough. Also, we have to make the

system stable if it is an unstable system. Especially,

in this research, the system is unstable due to time-

delay elements. As we expressed in the background

of this research, we tried the classical control (PID

Controller) and modern control (LQI method). As a

result, for PID controller if time-delay is large,

system could not preserve the stability. But for

Modern scheme LQI method we could make the

system stable without error. However, for high

dimension and MIMO system we couldn’t design

the optimum controller because of complexity of

solving the Ricatti equation. Therefore, in this

research we propose the IMC method which is one

of the robust controllers.

3 INTERNAL MODEL CONTROL

FOR TIME-DELAY SYSTEM

Internal Model Controller is an optimum controller

which minimizes the effect of disturbance to output

signal and considers the uncertainty of control

object. Also in this research we consider the

existence of time-delay elements. Hence most of

systems would be an unstable system due to time-

delay elements. We suggest the IMC method to

modify the stability of the system and compensate

the output signal. The main reason that we suggest

the IMC method is due to consideration of the

uncertainty of control object and time-delay

elements. The effects of disturbance to output signal

are minimized and it can be correspondence to

MIMO (Multi Input and Multi Output) and high

dimension systems. In order to modify the unstable

system due to time-delay elements, we have

designed the internal model controller. Figure 2

shows the IMC system which “D” is external

disturbance to output signal, ”K” is Internal Model

Controller, ”P”, ”H” and “

”, “

” are actual

system, actual time-delay element and model

system, approximated and predicted time-delay

element, respectively.

Figure 2: Internal Model Controller including a round trip

time-delay elements and external disturbance.

Here through figure 2 the block diagram of IMC

method, we obtained relation between output and

reference signal as follows.

dKHPHMIKrPHMy )(

11 −−

−+=

(3)

Where,

HPHHPHG

~~~

−=Δ

GKIM

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

200

Since, in the above equation (3) external disturbance

multiplied by “

1−

−

” Which IMC

method minimizes the effect of disturbance. As a

result we consider the minimization of H

norm of

this coefficient. Equation (4), below, shows how to

derive “K” which is Internal Model Controller:

min KHPHMI

−

(4)

0)]

()

[(

∫

∞

∞−

−

∗−

−

∂

dKHPHMIKHPHMITr

[]

0)]

()

[(

)]

()

[(

−

−⇒=

−

−⇒

−

∗−

−⇒

∫

∂=

⎥

⎦

⎤

⎢

⎣

⎡

∂

∫∫

∞

∞−

−

∗−

−

∂

⇒

⎥

⎦

⎤

⎢

⎣

⎡

KHPHMIKHPHMI

KHPHMIKHPHMITr

KdKHPHMIKHPHMITr

πω

QPK

−

(5)

Where,

is stable and minimum phase filter with

condition of

IQ =)0(

4 UNCERTAINTY OF CONTROL

OBJECT AND TIME-DELAY

ELEMENT

In this case of IMC, we use the model of control

object and the actual control object which it is an

unknown system. So, as it obtained through equation

(4) when “K” is the inverse system of model, it is

optimum case. Although in the case of internal

model controller except the model system, it

requires to realize the predicted time-delay element.

Therefore, it has used the Pade approximation for

“

” which it is approximated time-delay i.e. time-

delay elements that it can be indicate as”

” has

shown as follows:

∑

−

≈

−

enLPadeH

)1(

(

(6)

Where,

)!(!!2

!)!2(

knkn

nkn

−

for ),...,2,1.,0( nk =

Here we consider this approximated time-delay

element as a transfer matrix.

⎥

⎦

⎤

⎢

⎣

⎡

(7)

But, remember that the dimension “n” of

approximated matrix must be the same as control

object dimension. The reason of this is that in the

multiplication of two matrix systems, both of them

are required to have the same dimension,

theoretically. Because of approximated time-delay

element is considered as a system matrix.

5 NUMERICAL ANALYSIS

For evaluating the IMC method we have select our

plant as Wind Turbine System. In general, wind

turbine is located in gale area in order to generate

more energy. Therefore, observation and controlling

the attitude of outputs of wind turbine is required

from distance. Thus, in system there would be delay

elements. The process of simulation is first to

simulate the step response of closed loop system

without controller then step response of disturbances

and finally step response of system with IMC

method for non-nominal case. Here, we assume that

system has 2 seconds of delay for each time-delay

element, forward delay and feedback delay. The

linear system of WTS shown as follows:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

110

116

ceInterferen

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

120

Actual Time-Delay Element:

−

= I

)2,2(

:ionApproximat Pade

= IPadeH

As it is clear for actual plant, it includes some

interferences effects that is as the same as

disturbances, due to plant is MIMO system. Hereby,

the IMC proper filter set as follows:

⎥

⎦

⎤

⎢

⎣

⎡

+Δ+

Lss

Where,

LLL

−=Δ

Results

From figure 3 it is clear that interference effects the

APPLICATION OF INTERNAL MODEL CONTROLLER FOR WIND TURBINE SYSTEM CONSIDERING

TIME-DELAY ELEMENT

201

0.5

1.5

2.5

From: In(1)

To: Out(1)

0 20 40 60 80 100 120

0.5

1.5

To: Out(2)

From: In( 2)

0 20 40 60 80 100 120

Step Response

Time ( s ec )

Amplitude

Figure 3: Step response without Controller.

-0.5

0.5

1.5

From: In( 1)

To: Out(1)

0 100 200 300

-0.5

0.5

1.5

To: Out(2)

From: In( 2)

0 100 200 300

Step Response

Time ( sec )

Amplitude

Figure 4: Step response of disturbance with Controller.

0.5

1.5

From: In( 1)

To: Out(1)

0 100 200 300

-0.5

0.5

1.5

To: Out(2)

From: In( 2)

0 100 200 300

Step Response

Time

(

sec

)

Amplitude

Figure 5: Step response of closed-loop with Controller.

output signal as the same as disturbances. This may

cause the instability in closed loop system.

Therefore, Internal Model Controller method is

implied. Also the step response of disturbances is

confirmed in figure 4 that it converges to zero.

Figure 5, shows the step response of IMC. It is clear

that even though the step response of closed-loop

system contain with some effects of interferences,

still it converges to reference signal. Also the effect

of disturbances is almost cancelled. However, even

though the closed-loop is stable but the performance

of system is poor due to existence interferences and

time-delay element. Therefore, for future works

interferences cancelation and reduction of time-

delay effects is required in order to improve the

closed loop performances.

6 CONCLUSIONS

In this research internal model controller stabilize

the closed-loop system including round trip delay.

However, for proposed controller it considered the

uncertainty of plant and approximated time-delay

element. Therefore, even though system is non-

nominal, internal model controller can be

corresponded. For the system’s performance it can

be adjusted with proper filter and filter it’s self

automatically adjust the damping factor by ΔL

which is uncertainty of time-delay, in other words

the IMC proper filter is a semi-adaptive filter.

However the demerit point of Internal Model

Controller is for non-nominal case the performance

of system is poor. Therefore, minimizing the

uncertainty system ΔG is become one of the

important issue. Also interference cancellation is

required in order to realize better performance.

REFERENCES

R. C. Dorf, R. H .Bishop, 2002 “Modern ControlSystem”,

Prentice Hall

Witold Pedrycz, 2007 “Robust Control Design an Optimal

control Approach” Wiley

G. F. Franklin, J.D.Powell, M.Workman, 1997,”Digital [4]

Control Dynamic System” Addison –Wesley

R. Oboe, K. Natori, K. Ohnishi, 2008, ”A Novel Structure

of Time DelayControl System with Communication

Disturbance Observe” IEEE

J. E. Normey-Rico and E.F. Camach, 2007, “Control of

dead time processes” Springer

G. Chesi, A. Garulli, A. Tesi, A. Vicino, 2009,

“Homogeneous Polynomial Forms for Robustness

Analysis of Uncertain Systems.” Springer

G. Gu, J. Chen and E. Lee “Parametric H Infinity Loop-

shaping and Weighted Mixed Sensitivity

Minimization” IEEE ’99 Transactions on Automatic

Control, Vol. 44, no. 4, pp. 846-852, 1999

Sigurd Skogestad, Ian Postlethwaite, 1996 “Multi Variabla

Feedback Control Analysis and Design” John Wiey

F .Asharif, S.Tamaki, T.Nagado, T,Nagata, M. Rashid, M.

Asharif , 2009, “Feedback Control of Linear Quadratic

Integration Including Time-Delay System” ITC-CSCC

Duncan Mc Farlane and Keith Glover “An H Infinity

Design Procedure Using Robust Stabilization of

Normalized Coprime Factors” The 27th IEEE

Conference on Decision and Control, December 1998,

No. 88CH2531-2, pp. 1343-1348

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

202