
FINDING THE BEST GRASPING POINT IN OBJECT
MANIPULATION TASKS
A Comparison between GA and PSO Methods
Hamed Mesgari, Farzad Cheraghpour
Dep. of Mechanical Engineering, K.N. Toosi University of Technology, Vanak Square, Tehran, Iran
S. Ali A. Moosavian
Dep. of Mechanical Engineering, K.N. Toosi University of Technology, Vanak Square, Tehran, Iran
Keywords: Optimization, Performance index, Object manipulation, Robotic manipulator, Grasping, Particle Swarm
Optimization, Genetic Algorithm.
Abstract: Grasp planning is one of the most interesting subjects of object manipulation tasks in robotics and the
development of grasp methods would be affected the robot performance. One of the most important subjects
which is discussed in grasp planning, especially in industrial applications, is optimal grasp planning and
finding the best grasping point. So it is important to find the best grasping point that the manipulator contact
with object. In this paper, the MAG performance index, which is designed for object manipulation tasks,
would be used for two different types of objects which are manipulated in the predefined path. Particle
Swarm Optimization (PSO) and Genetic Algorithm (GA) methods would be used to maximize this index
and find the best grasping point and finally compared with each other. The results show that in faster object
manipulation tasks, the GA method is more suitable than PSO method. Since in accurate object
manipulation tasks, the PSO method is preferred to GA method.
1 INTRODUCTION
Object manipulation is defined as the translation or
change in objects orientation by robot manipulators.
For a translation task, robot manipulator moves a
body by exerting appropriate joint forces and torques
after contacting with that. For object manipulation,
we can define several goals, e.g. turning a switch,
opening a door, polishing a surface, translation of a
vehicle engine in a production line, etc. One of the
most important things which are studying in object
manipulation is how body and robotic arms are
relating. This process is called grasp.
A good grasp must have several properties which
categorized in five principal groups, i.e. force
closure, equilibrium, stability, dexterity and dynamic
response (Hester et al., 1998). Thus an index must
be used to satisfy these grasp properties. Several
researches had been done on grasp planning in two
last decades. Some non-dimensional indices are
defined to evaluate grasp function. In one vision
(Cheraghpour et al., 2009), grasp principal
properties are classified into three main groups. In
the first group, the indices choose the appropriate
grasping points on object, which shows itself in
equations by grasp matrix, represent the kinematics
parameters of robot arm and grasped object. In the
second group, the indices choose the appropriate
configuration of robotic arm. Since there are several
responses for accessing of a robot arm to a point in
work space by calculation of inverse kinematics, the
answer must satisfy kinematics specifications like
dexterity and move capabilities. In the third group,
the indices are related to kinetics of robot
manipulator and grasped body after grasp process
and during the manipulation.
In other vision (Byoung et al., 2001), other non-
dimension indices are presented which included
other grasp properties like stability grasp index,
uncertainty grasp index, maximum force
transmission ratio index, task isotropy index and
stiffness mapping-based grasp isotropy index. With
199
Mesgari H., Cheraghpour F. and Ali A. Moosavian S..
FINDING THE BEST GRASPING POINT IN OBJECT MANIPULATION TASKS - A Comparison between GA and PSO Methods.
DOI: 10.5220/0003532001990204
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 199-204
ISBN: 978-989-8425-75-1
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

these in mind, Multi Aspect Grasp (MAG)
performance index (Cheraghpour et al., 2009) is
chosen to evaluate the grasp quality for object
manipulation in the predefined task.
Numerical solution methods are powerful tools
which can be used to solve problems, especially in
nonlinear problems numerical methods are more
suitable and useful than analytical solutions. Among
all these methods, Particle Swarm Optimization
(PSO) method and Genetic Algorithm (GA) are used
so widely in solving problems (Mannepalli et al.,
2010). These methods, especially PSO method, are
developed so widely in recent years (Kaviani, Fathi,
Farokhnia and Ardakani, 2009). Besides, PSO and
GA method are so fast and easy to use and their
results are so trustworthy (Martinez et al., 2009).
In this paper, Particle Swarm Optimization
(PSO) method and Genetic Algorithm (GA) would
be used to find the best grasping point of two
different objects according to maximizing the MAG
performance index and the results would be
compared with each other.
2 THE MAG INDEX
The Multi Aspects Grasp (MAG) performance index
is defined as (Cheraghpour et al., 2009):
0
12 3
max max
1
1
f
t
ii
N
ii
t
DP
M
AG W C W W dt
tDP
⎡⎤
⎛⎞
=++−
⎢⎥
⎜⎟
Δ
⎢⎥
⎝⎠
⎣⎦
∫
(1)
where t
0
and t
f
denote initial and final times of
simulation respectively, ∆t= t
f
- t
0
, weighting factors
W
1
, W
2
and W
3
are defined to put different
emphasizes on each term. In Eq. 1 C
N
is defined as
the inverse of condition number of grasp matrix, i.e.
G:
(
)
()
min
max
N
G
C
G
σ
σ
=
(2)
Also, the term D is related to move ability of robotic
arm and defined as:
(
)
**
det
T
D
JJ=
(3)
where J
*
denotes the Jacobian matrix which maps
robotic arm joints velocity space to grasped object
center of gravity velocity. Finally, the term P is
related to power consumption of robotic actuators
and defined as:
.
.
T
P
dt dt
θτ
⎡
⎤
=
⎢
⎥
⎢
⎥
⎣
⎦
∫∫
(4)
Note that in Eq. 1 the terms D
max
and P
max
denoted
the maximum values of D and P respectively in the
predefined task.
3 PSO METHOD
Particle Swarm Optimization (PSO) is a global
optimization method which is presented first by
Russell and Kennedy in 1995 (Atyabi et al., 2009).
PSO is a search method which is inspired from the
group behavior of animals like birds and fishes. The
main advantageous of PSO over other optimization
methods is the plenty existence of particles. Besides,
in nonlinear problems derivations of performance
index are so sophisticated whereas PSO is needless
of performance index derivations which made this
method so useful in solving nonlinear problems.
In this method, every particle is the representative of
problem solution which is moving in the search
space until approaches to the best position. At
starter, the position and velocity of every particle are
chosen randomly and then the value of particles is
calculated based on a merit criterion by moving in
the response space. Thus all particles accelerated
toward the best solution of problem step by step.
There is a memory is PSO which can save the best
position gained by every particle in P
i
and the best
position gained by all particles in P
g
during
simulation and in every step, i.e. iteration. The
velocity of particles is corrected by random
coefficient in the direction of these two positions.
This fact is shown by constraints Eq. 5 and Eq. 6 and
Figure (1):
11 2 2
(1) () ()() ()()
ii ii gi
vt wvtcRPtxt cRPtxt
→→→→ →→
⎛⎞⎛
⎞
+= + − + −
⎜⎟⎜
⎟
⎝⎠⎝
⎠
(5)
Where v
i
and x
i
are position and velocity of i-th
particle respectively, R
1
and R
2
are random
coefficients between 0 to 1 and c
1
and c
2
are
arbitrary constants. Parameter t denoted the
calculation step. Thus the new position of particles is
calculated as:
(1) () (1)
iii
xt xt vt
→→→
+
=++
(6)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
200

Figure 1: Principle of PSO method and the process of
achieving to new position.
The term inertia weight w in Eq. 5 is declined
linearly with time:
()
()
12 2
max
max
iter t
www w
iter
−
=−× +
(7)
where w is inertia weight, w
1
and w
2
are the initial
and final inertia weights respectively, t is the
iteration step and maxiter is the termination
iteration. The inertia weight term control the
effectiveness of one step back velocity on the
solution finding task.
4 SIMULATION
4.1 Robotic Manipulator
Figure (2) shows a robotic manipulator performing
the object manipulation task, i.e. moving the object
through the predefined path. The system includes a
RRR manipulator. The inertial and geometrical
parameters of manipulator arms are shown in Table
(1). Note that the unit of I
xx
, I
yy
and I
zz
in Table (1) is
kg.m
2
.
Figure 2: The SCARA type manipulator grasps a
rectangular object.
Table 1: Manipulator inertial and geometrical parameters.
zz
I
y
y
I
x
x
I
m[kg] L[m] Link
0.539 0.524 0.13017.41.041
0.539 0.524 0.13017.41.042
0.192 0.212 0.015 6.1 0.92 3
4.2 Task
The task is moving the object on the straight line
along X-axis. Joints trajectory are quintic functions
as follows (Craig, 2005):
2345
012345
0
()
() 1
() 10
5(sec)
f
Xtaatatatatat
Yt
t
t
ψ
=+++++
=
=
=
(8)
The predefined path, grasping point coordinates with
respect to object center of mass and also the DH
coordinates of each link of the manipulator are
shown in Figure (3).
Figure 3: Predefined path for object center of mass in a 2D
task, the position of grasping points with respect to C.G.
of object and DH coordinates.
The grasp is supposed to be solid, i.e. the object
orientation cannot change with respect to the End-
Effector. The MAG index is calculated for two types
of objects, i.e.
1.25 0.55
mm
×
rectangular (No.1) and
20.3
mm
×
long bar (No.2). The inertial parameters
of objects No.1 and No.2 are shown in Table (2).
Table 2: Grasped objects inertial parameters.
zz
I
y
y
I
x
x
I
m [kg] Object No
3.4612.9030.56522.27 1
6.6266.4830.14919.44 2
x
i
(t)
x
i
(t+1)
P
i
P
g
v
i
(t)
FINDING THE BEST GRASPING POINT IN OBJECT MANIPULATION TASKS - A Comparison between GA and PSO
Methods
201
Note that the unit of I
xx
, I
yy
and I
zz
in Table (2) is
kg.m
2
.
Also weighting factors W
1
, W
2
and W
3
in Eq. 1 are
supposed to be equal, i.e. all the terms have the same
importance in object manipulation task.
4.3 PSO Method Parameters
We developed a program for calculation of MAG
index from object surface points which is coded in
MATLAB program. Basic PSO parameters which
are illustrated in Eq. 5, Eq. 6 and Eq.7 are shown in
Table (3) (Shi and Eberhart, 1999).
Table 3: Basic PSO parameters.
Parameters Objects No.1 and No.2
V
max
1
V
min
0
x -
y -
c
1
1.4
c
2
1.4
w
1
0.4
w
2
0.9
Agents 20 particles
Elimination time 60 iterations
where V
max
and V
min
are the upper and lower
boundary values of initial velocity respectively, x
and y are initial values of grasping points position
with respect to object center of mass which are
randomly selected on the object surface, c
1
and c
2
are fixed constants in Eq. 5, w
1
and w
2
are the initial
and final inertia weights respectively used in Eq. 7
(Samanta and Nataraj, 2009), agents and elimination
time are the number of particles which search in
response space and the total iterations needed to
converge the answers respectively which are
obtained heuristically (Atyabi et al., 2009). Note that
agents are the representatives of the problem
solution, i.e. the best grasping points of object which
maximize the MAG index.
4.4 GA Parameters
We use MATLAB Genetic Algorithm toolbox to
maximize MAG index and find the position of the
best grasping point. In the toolbox, MAG index and
the geometrical dimensions of object are selected as
fitness function and inputs respectively. The
simulation parameters are shown in Table (4).
Generation and population size are obtained
heuristically, i.e. more generation and population
size values do not make any differences is results
and these are the minimum values that results
needed to be converged. Since there is no constraint
in problem, mutation function is selected as
constraint dependant. Other parameters are selected
according to their definition (Goldberg, 1997).
Table 4: GA parameters.
Parameters Object No.1 and No.2
Population size 20
Fitness scaling function Rank
Selection function Stochastic uniform
Crossover fraction 0.8
Crossover function Scattered
Mutation function Constraint dependant
Generation 40
Migration fraction 0.2
Migration interval 20
5 RESULTS AND DISCUSSION
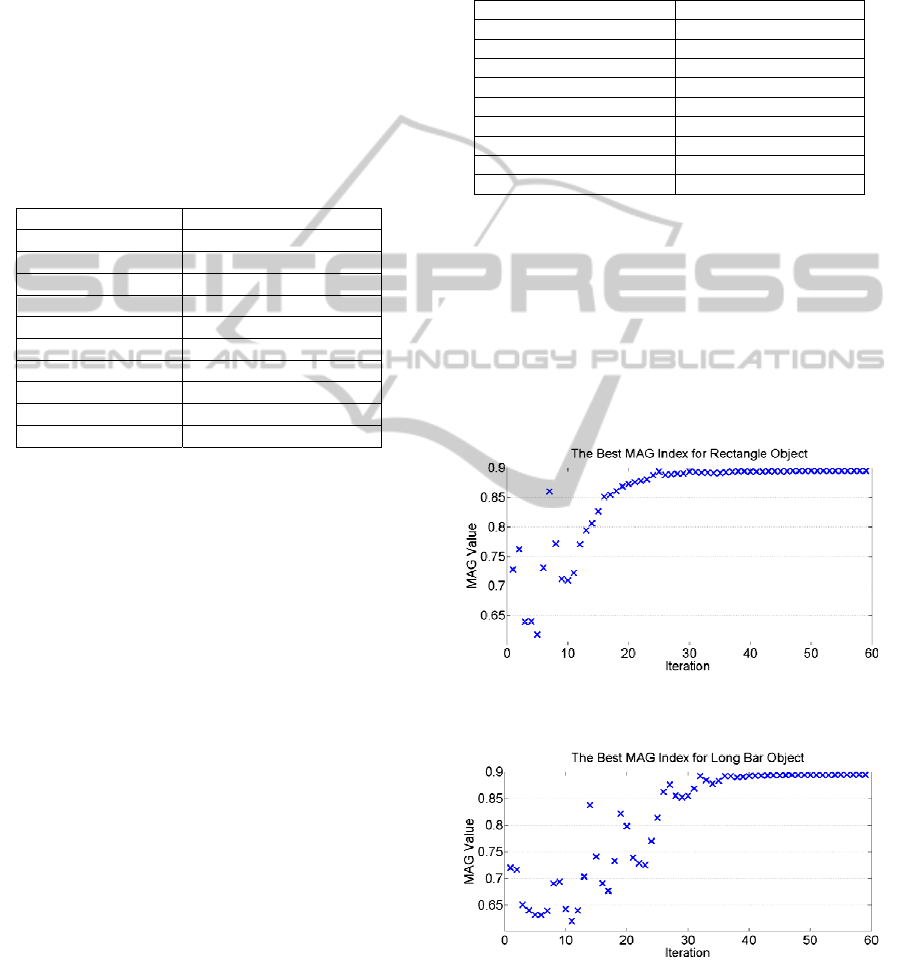
The results of MAG index value obtained from PSO
method for rectangular (No.1) and long bar (No.2)
objects are shown in Figure (4) and Figure (5). The
results show that the MAG value for both
rectangular and long bar object is about 89 percent
for the best grasping point.
Figure 4: MAG index value for the best grasping point for
rectangular object calculated by PSO method.
Figure 5: MAG index value for the best grasping point for
long bar object calculated by PSO method.
The best grasping points of objects obtained from
PSO method are shown in Figure (6) and Figure (7).
The results show that the best grasping points are
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
202
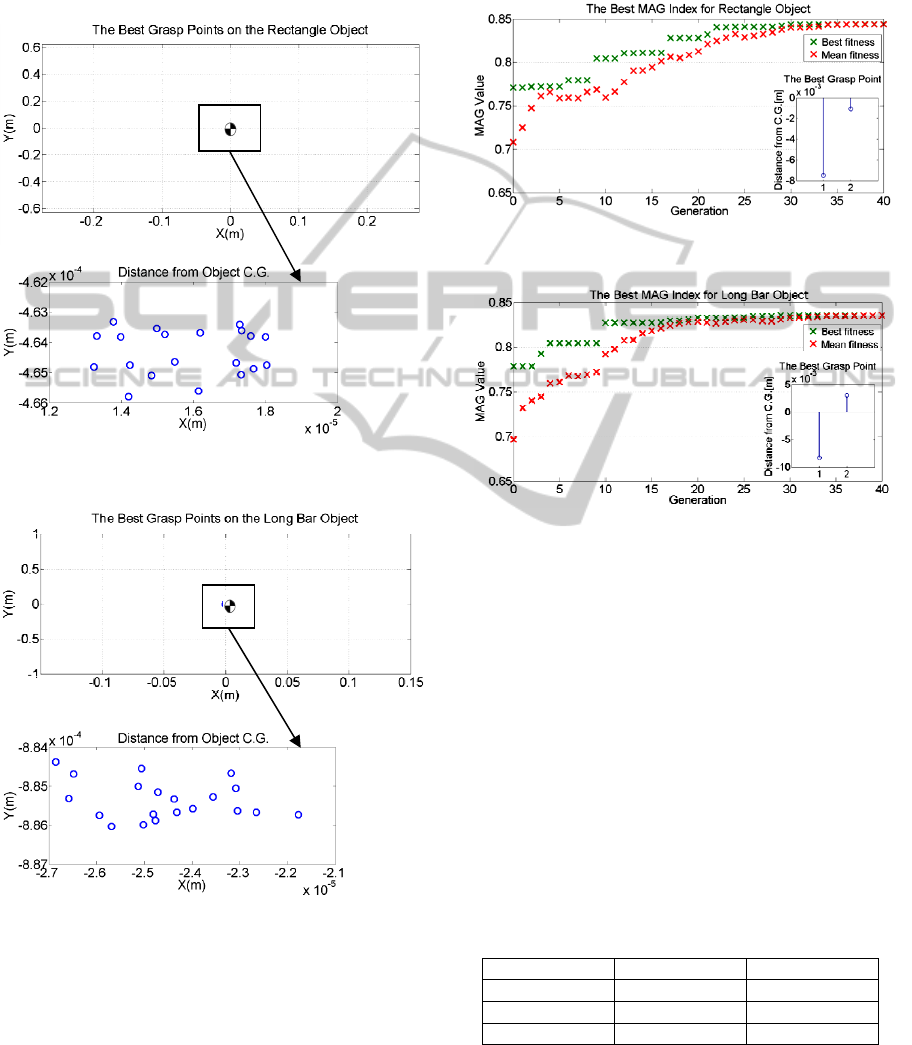
closed to object center of gravity. It is analytically
proved that the best grasping point must be closed to
the object center of gravity, i.e. the maximum MAG
performance index value is belong to the best
grasping point which is the object center of gravity
(Cheraghpour et al., 2010).
Figure 6: The best grasping points for rectangular object
calculated by PSO method and their magnified positions.
Figure 7: The best grasping points for long bar object
calculated by PSO method and their magnified positions.
The results obtained from GA for object No.1 and
object No.2 are shown in Figure (8) and Figure (9).
The results show that MAG index value for
rectangular and long bar object are about 84 and 83
percent respectively for the best grasping point
which is closed to object center of gravity
(Cheraghpour et al., 2010).
Note that in Figure (8) and Figure (9), 1 and 2
represented the x and y coordinates of grasping point
position respectively which are measured from
object center of gravity.
Figure 8: MAG index value for the best grasping point for
rectangular object calculated by GA method.
Figure 9: MAG index value for the best grasping point for
long bar object calculated by GA method.
The results show that maximum MAG index value
which is obtained from PSO method is more than
GA method, i.e. MAG index value obtained from
PSO method for both object NO.1 and object NO.2
is 89 percent whereas MAG index value obtained
from GA for object NO.1 and object are 84 and 83
percent respectively for the grasping point which is
closed to object center of gravity. Besides, the best
grasping point obtained from PSO method is closer
to object center of gravity than the result of GA one.
Also, program processing times on an Intel CPU
2.8 GHz for GA and PSO method are shown in
Table (5).
Table 5: A comparison between approximated processing
time of GA and PSO methods.
time (sec) time (sec)
Method object No.1 object No.2
PSO 236 238
GA 150 152
The Table (2) shows that GA is converging faster
than PSO method, i.e. processing time of GA is less
than PSO method.
FINDING THE BEST GRASPING POINT IN OBJECT MANIPULATION TASKS - A Comparison between GA and PSO
Methods
203

6 CONCLUSIONS AND FUTURE
WORK
In this paper, MAG performance index is selected to
evaluate grasp quality of object manipulated in the
predefined path. Two numerical solution methods
were used and compared with each other. Particle
Swarm Optimization (PSO) method and Genetic
Algorithm (GA) were used to maximize this index
and find the best grasping point for object
manipulation in the predefined task. Two different
kinds of objects were used as the case studies. The
results show that the maximum value of MAG index
obtained from PSO method is more than maximum
value which is obtained from GA one. Besides, both
methods show that the best grasping point is closed
to object center of gravity, which was analytically
proved. Also the results of GA method are
converged faster than PSO method but with different
accuracies, i.e. PSO method had more accurate
results than GA one. Therefore, in faster object
manipulation tasks, the GA method is more suitable
than PSO method. Since, in accurate object
manipulation tasks, the PSO method is preferred to
GA method.
In the future, we would like to do this procedure
for unsymmetrical objects. Also for spatial and
wheeled mobile manipulators (WMM), which has
the geometrical constraints of object and the
manipulator is more sophisticated, the problem
could be more interesting. For online problems, e.g.
facing to a new object, soft computing methods like
neural networks, fuzzy logic and neuro-fuzzy would
be used and compare.
REFERENCES
Hester, R., Cetin, M., Kapoor, Ch,. Tesar, D., 1998. A
criteria-based approach to grasp synthesis, The
University of Texas at Austin.
Cheraghpour, F., Moosavian, A., Nahvi, A., 2009.
Multiple Aspect Grasp Performance Index for
Cooperative Object Manipulation Tasks. IEEE/ASME
International Conference on Advanced Intelligent
Mechatronics, IEEE Press.
Byoung, H., Sang-Rok, O., Byung-Ju, Y., Hong, S., 2001.
Optimal Grasping Based on Non-Dimensionalized
Performance Indices, Proceedings of the 2001
IEEE/RSJ. IEEE Press.
Mannepalli, S., Dutta, A., Saxena, A., 2010. A multi-
objective GA based algorithm for 2D form and force
closure grasp of prismatic objects, Int. Journal of
Robotics and Automation.
Kaviani, A. K., Fathi, S. H., Farokhnia, N., Ardakani, A.
J., 2009. PSO, an effective tool for harmonics elimination
and optimization in multi-level inverters, 4th IEEE
Conference on Industrial Electronics and
Applications, ICIEA 2009, IEEE Press.
Martinez, R., Castillo, O., Aguilar, L., 2009. Optimization
of interval type-2 fuzzy logic controllers for a
perturbed autonomous wheeled mobile robot using
genetic algorithms, Elsevier Press.
Atyabi, A., Phon-Amnuaisuk, S., Chin Kuan, H., 2009.
Applying Area Extension PSO in Robotic Swarm,
Springer Science and Business Media, Springer Press.
Craig, J., 2005. Introduction to Robotics; Mechanics and
Control, Addison-Wesley Publishing, 2nd edition.
Shi, Y., Eberhart, R., 1999. Empirical study of particle
swarm optimization, Proceedings of IEEE Congress
on Evolutionary Computation, Piscataway, NJ, USA,
IEEE Press.
Samanta, B., Nataraj, C., 2009. Application of particle
swarm optimization and proximal support vector
machines for fault detection, Published in Springer
Science and Business Media, LLC, Springer Press.
D. E. Goldberg, 1997. Genetic Algorithm in search,
Optimization, and Machine Learning, Prentice-Hall
International, Inc.
Cheraghpour, F., Moosavian, A., Nahvi, A., 2010. Robotic
Grasp Planning by Multiple Aspects Grasp Index for
Object Manipulation Tasks, Proceeding of ICEE2010,
Isfahan University of Technology.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
204
