ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

Emanuel Dogaru, Cristina Stoica and Emmanuel Godoy

Automatic Control Department, SUPELEC Systems Sciences (E3S), 3 rue Joliot Curie, 91192, Gif sur Yvette, France

Keywords: Model Predictive Control, Youla-Kučera Parameter, Unstructured Uncertainties, Linear Matrix Inequality,

Multivariable Systems, Linear Quadratic Control, Robot Control.

Abstract: This paper presents the application of several advanced control techniques to a nonlinear strongly coupled

multivariable robot. The main difficulties come from the flexibility of the mechanical chain, but also from

the lack of joints sensors. In a first stage, a state-feedback linear quadratic (LQG) technique and a model

predictive control (MPC) are designed using optimal observers. Considering additional sensors that provide

measurements of accelerations increases the robustness of the controlled system. The second stage consists

into adding a supplementary robustness layer (i.e. explicitly considering the robust stability under

unstructured uncertainties) on the stabilizing MPC developed at the previous stage. Comparative results are

proposed highlighting the trade-off between robust stability and nominal performance for disturbances

rejection.

1 INTRODUCTION

Robots are nonlinear, often multivariable systems,

with a strong interaction between their components.

Modelling procedures (Book, 1989, Spong et al.,

2005, Sciavicco and Siciliano, 1996) for robots can

be difficult, leading sometimes to sophisticated

models, which cannot be used for control. In

addition, the models have to offer an accurate image

of the real robots, while preserving the simplicity.

Neglected or poorly known dynamics can affect the

behaviour of the controlled robots. Therefore a need

for robust control techniques is identified. Different

control laws have been developed: robust state-

feedback controllers (Tomei, 1994), output-feedback

controllers (Moreno-Valenzuela et al., 2008), robust

nonlinear control for robots with parametric

uncertainties (Spong, 1992), LPV (linear parameter

variant) control (Halalchi et al., 2010). Predictive

control has also been applied on robots (Merabet and

Gu, 2009, Maalouf, 2006,

Hedjar et al., 2002).

This paper proposes an application of robustified

control techniques to a medical robot (Al Assad et

al., 2008), which is a nonlinear multivariable

strongly-coupled system. In fact, this paper is an

extension of the work proposed by (Stoica et al.,

2009) in which a monovariable model of the pivot

(only one axis model) of the same robot is studied.

In this paper, we consider two stabilizing initial

control laws (linear quadratic control and predictive

control) for a two axes model of the robot. In order

to explicitly guarantee robust stability under

unstructured uncertainties, an offline robustification

procedure of the initial stabilizing MPC (Model

Predictive Control) law is proposed. This

robustification method is based on the optimization

of a Youla-Kučera parameter also known as the Q

parameter. Addressing the robust stability under

unstructured uncertainties leads to a convex

optimization problem, solved with LMI (Linear

Matrix Inequality) tools. The advantage of this

robustification method is that it unifies the qualities

of both robust control and predictive control, while

keeping a simple implementation: a feedback-gain

coupled with an observer gain and a Youla

parameter. The main novelty of this paper is the

application of the proposed robustified controllers

on the multivariable two axes model of the robot.

The proposed approach is an alternative to the

current implemented structure based on LQ (linear

quadratic) regulators for each axis (Al Assad et al.,

2007).

This paper is organized as follows. Section 2

describes the medical robot, offering a Lagrange

model for the Pivot and C-arc system. Section 3

deals with control strategies applied on the robot,

while Section 4 offers some details about the

technique used to robustify the MPC controller.

Section 5 focuses on an analysis of the results

290

Dogaru E., Stoica C. and Godoy E..

ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT.

DOI: 10.5220/0003534002900299

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 290-299

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

obtained with the proposed control laws. Finally,

some concluding remarks and perspectives are given

in Section 6.

2 DESCRIPTION OF THE ROBOT

The system considered in this paper is a vascular

robot (Al Assad et al., 2008) developed by General

Electric Healthcare and used for medical X-ray

imaging. It is a four-degree of freedom open-chain

robot composed of the following links: the L-arm

(revolute joint), the pivot (revolute joint), the C-arc

(which can be considered as a revolute joint around

a virtual axis crossing the C-arc centre) and the lift

(prismatic joint). Each joint is driven using a DC

motor.

The robot is a nonlinear system (especially due

to the irreversibility of worm gears) and a strongly

coupled multivariable system (due to the

interconnection of its joints). The model takes into

account the hard nonlinearities of the system such as

joints friction and gear’s irreversibility. The

flexibility of each axis is modelled as a two-mass

spring system representing one vibrating mode

(Fig. 1). A detailed model of the entire robot can be

found in (Al Assad et al., 2008).

Drive chain

Damping



Load torque

Stiffness



Figure 1: Two-mass spring system.

This paper considers the flexible model of only

two axes: the pivot and the C-arc. The other two

axes (the L-arm and the lift) were considered to be

fixed. The dynamics of this model is given by the

following Lagrange equations:











)()(),()( q

qqqqqqq

KQCDA

ΓKFJ





(1)

where





 and



mmm



 are

respectively the vectors of joints angular position

and motors shaft angular position of the pivot and

the C-arc. More exactly, the index ‘2’ is further used

for the pivot elements, ‘3’ denotes the C-arc

elements and the index ‘m’ is used for each motor.

),diag(

32 mmm



J , ),diag(

32 vvv



F ,

),diag(



K and ),diag(



D are diagonal

matrices belonging to

22

 which contain the

parameters of each axis: inertia (

J ), viscous

friction (

F ), joint stiffness (k) and respectively

joint damping (d). The matrix

)(



qA

is the

robot inertia matrix, the vector

),(



qq



represents the Coriolis and centrifugal torque/forces,

)(



qQ represents the gravitational forces

vector and









mmm

Γ is the input

torques vector (in fact the vector of control signals).

The matrices from (1) can be detailed as:



cos)cossin(

)(

),(,

23333

1211

1312

2221

1211





































































MYMXg







with the following notations:

2333312

222211

333321

333313

333312

322

333321

323312

3333

3211

sin)cossin(

)cossin(

)2(cossincos

cossin

)2(cos2sincos2

sincos

sincos2cos















MYMXgq

XYXXc

YZXZc

XYXXc

ZZa

YZXZa

XYXXZZa













The notations

3333322

,,,,,, ZZYZXZXYXXZZYZ

refer to the inertia moments of

the pivot or the C-arc, expressed in the

corresponding coordinate.

Equation (1) can be rewritten as a nonlinear

state-space representation:



























mmvmm

qqq

qqqqqqq







)(

)(),()()(

KFΓJ

QCDKA

(2)

where the state of the model is defined as





qqqqx



 .

ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

291

3 CONTROL STRATEGIES

This section presents the theoretical background of

the LQG and MPC control techniques that will be

applied on the nonlinear system (1).

For control design purposes the nonlinear model

(2) is linearized around an operating point

x leading

to the following continuous time LTI (linear time

invariant) state-space representation:















)()(

)()()(

txCtz

txCty

tuBtxAtx



(3)

where



 ,



 ,



 ,



 .



)(  represents the

vector of the control signals,

qty )( represents

the vector of the controlled signals and

)(tz is the

vector of the measured signals. Usually, available

sensors in robot arms can provide only the velocity

and the position of the motor shaft. In order to

increase the robustness of the control law, additional

sensors will be considered to measure the joints

accelerations. This leads to



qqtz



)( and

















, where



contains only the first two

lines of the

A matrix.

3.1 State Feedback LQG Control

A state feedback control scheme is considered as a

first approach. Consider the LTI system (3). If the

pair (

BA , ) is stabilizable and (

CA , ) is

detectable then the control law that optimizes the

cost function (4) is given by

)()(

txLtu  .









)()()()(

dttuRtutxQtxJ

(4)

In order to cancel the static errors an integral

action on the motor shaft position error



 dtdtqq

spm

)(



is added (with

the set-

point of the motors shaft angular position), leading

to the following augmented state vector





dtqqqqx





















. The new matrices

of the augmented state representation are:



ppzcI

ppy

pnc































(5)

Finally, since the sensors do not provide all the

states, an observer (6) is incorporated into the

control procedure:



)(

)()()(

)(

txCtzKtuBtxAtx

zcc





(6)

In order to minimise the influence of the

observer on the control law robustness (Doyle and

Stein, 1979), an asymptotic Kalman filter is

proposed as observer:

111



 WCK

(7)

where



is the unique positive definite solution of

the Riccati equation:

11111





CWCVAA

(8)

and ,,

WVRQ

are symmetric positive definite

weighting matrices that will be used as tuning

parameters.

3.2 Model Predictive Control (MPC)

The second control technique applied on the two

axis model (1) is an unconstrained MPC. The

motivation of this choice consists in the MPC’s

capacity of handling multivariables systems

(Camacho and Bordons, 2004, Maciejowski, 2001).

The model used by MPC is obtained from (3) after

discretizing with a sample time

T :















)()(

)()()1(

kxCkz

kxCky

kuBkxAkx

(9)

with



 and . For the steady state

errors cancellation, an integral action on the control

signal

)()1()( kukuku









is added leading to

the extended state-space representation described by:



mpzdI

mnm































(10)

with



kukxkx )1()()( 

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

292

In order to design the MPC gain the following

criterion is minimised:











)()()(

ikuikxikxJ

(11)

using as tuning parameters: the prediction horizons

, NN , the control horizon

N and the weightings

. Here

represents the set-point of the

state vector. It is considered that

Niiku  ,0)( . The states are calculated

using the prediction model (9) as follows:











)()(

)(

dII

jkuBAkxAikx

(12)

with the state estimation

)(

obtained from the

optimal Kalman filter:

))(

)(()()(

)1(

kxCkzKkuBkxAkx

IdIdIIdII



(13)

where

2222

)(



 WCCCAK

dIdI

and



the unique positive definite solution of the algebraic

Riccati equation:

222

)( 



 T

dIdI

ACWCCCA

VAA

(14)

and WV are symmetric positive definite weighting

matrices used as tuning parameters for the observer.

Next, applying the receding horizon principle, which

is specific to predictive control, the following

control law is obtained:

)(

)()(

kxLkxFku

Ispsp



(15)

with the set-point pre-filter

F and the MPC gain

L (Fig. 3 and Fig. 4).

4 ROBUSTIFIED MPC

This subsection focuses on the procedure used to

enhance robustness to the Model Predictive Control

law developed in the Section 3.2. The basic idea is

to add a stable Youla-Kučera parameter (Kučera,

1974, Youla et al., 1976) to parameterize the class of

all stabilizing controllers starting from an initial

stabilizing state-feedback controller coupled with an

observer. This approach is known in the literature as

the modified controller paradigm (Boyd and Barratt,

1991, Maciejowski, 1989) and consists into

modifying the initial stabilizing controller by adding

an auxiliary input



and an output y



with a zero

transfer in between Fig. 2). This procedure enables

to find a controller belonging to the class of all

stabilizing controllers that will improve the

robustness of the initial control law, without

changing the initial Input/Output behaviour (i.e. the

transfer from

w to z) of the initial closed-loop in the

absence of disturbances.

Figure 2: Class of all stabilizing controllers.

The transfer

T can be represented using the

LLFT (Lower Linear Fractional Transformation)

form of the initial controlled system coupled with

the Youla-Kučera parameter, denoted Q parameter,

with



zwzwzw

TQTTT

zw 211211





(16)

Note that this structure is affine in the Q parameter,

allowing convex specifications in closed-loop.

The next step is to apply this strategy to the

MPC law proposed in Section 3.2. Different

scenarios can be considered depending on the choice

of the transfer

T . For instance, if the aim is to

improve stability robustness under additive

unstructured uncertainties, then the following choice

has to be done

bzzw



(Fig. 3). For robust

stability under multiplicative uncertainties, the

following transfer has to be considered

bzzw



(Fig. 4), which is equivalent to the complementary

sensitivity function.

Figure 3: Robustification under additive unstructured

uncertainties.















1211

zwzw



ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

293

Figure 4: Robustification under multiplicative

unstructured uncertainties.

In order to improve the robustness of the initial

control the following optimization problem has to be

solved:

a. Find



 HQ that improves the robust

stability under additive unstructured uncertainties

solving:













ubu

TWT minmin

(17)

Find



 HQ that improves the robust

stability to multiplicative unstructured uncertainties

solving:













byy

TWT

minmin

(18)

Here

W and

W denote appropriate weighting

terms chosen in order to accomplish the desired

robustness specifications in a specified frequency

range.

As the robustification procedure is identical for

both additive and multiplicative uncertainties, the

notation

T will be further used for the general

case.

Since the Q parameter initially varies in the

infinite-dimensional space of stable transfers

(



H ), it is suitable to restrict the search. A sub-

optimal solution (Scherer 2000) is to consider a FIR

(Finite Impulse Response) filter. The state-space

form





QQQQ

,D,C,BA of this multivariable Q

parameter will be further used, with a known (a

priori fixed) pair



yQyQyQy

pnpnpnp

,BA





and an unknown pair



yQy

pmnpm

,DC





that will result from the optimization procedure (see

(Stoica et al., 2007) for more details). Here

denotes the degree of the Q polynomial. The

optimization problems (17) and (18) can be

reformulated as a matrix inequality using the

following theorem.

Bounded real lemma (Boyd et al., 1994,

Scherer, 2000, Clement and Duc, 2000). A linear

discrete time invariant system with the state-space

representation





clclclcl

,D,C,BA

is stable and has a



H norm lower than



if and only if:





















IγDC

DIγB

CXA

BAX

/XX

clcl

(19)

with “ 0 ” (“ 0 ”) denoting a strictly positive

(negative) definite matrix.

Using a change of variables and two congruence

transformations (Scherer, 2000, Clement and Duc,

2000), the expression (19 can be further transformed

into a LMI (Linear Matrix Inequality) with the

decision variables:

X ,



and the Q parameter

hidden in the closed-loop matrices. An exact form of

this LMI and also the entire procedure (which is

outside the aim of this paper) leading to this LMI

can be found in (Stoica et al., 2007).

Hence, depending on the considered transfer

minimisation, the resulting optimization problem is

the following:

only robust stability under additive unstructured

uncertainties: minimize



subject to the Linear

Matrix Inequality

LMI using the state-space

representation





clclclcl

,D,C,BA

of the transfer

bzzw





min

LMI

(20)

only robust stability under multiplicative

unstructured uncertainties: minimize



subject to

the Linear Matrix Inequality

LMI using the state-

space representation





clclclcl

,D,C,BA

of the transfer

bzzw





LMI

min

(21)

robust stability under both additive and

multiplicative unstructured uncertainties: minimize a

given cost function subject to the two LMIs defined

before:

)(min

CSCS

LMILMI





(22)

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

294

where



cc ,

are weighting terms and





LMI and



 in

LMI .

Note that this robustification procedure can be

applied to every state-feedback controller coupled

with an observer. The particular case of MPC is used

here due to its good performance and simplicity of

implementation when dealing with multivariable

systems.

5 SIMULATION RESULTS

The control strategies proposed in this paper (LQG

control, MPC and robustified MPC) are now applied

to the nonlinear model (1). The LQG and MPC

control laws are designed to achieve the same

performances and to respect the admissible motors

torques.

The LQG controller is designed in continuous-

time in accordance to an existing LQ controller

(Stoica et al., 2009) which is already implemented

on the real robot.

The linearized continuous-time model (3) used

to design the LQG control law was obtained via the

Matlab

function ‘linmod’. A sample time

005.0

T s and a zero-order hold on the inputs

discretization method were used to determine the

prediction model (9) used by MPC.

5.1 Tuning Parameters

First of all, based only on the information of the

angular position sensors from the Pivot and C-arc a

LQG controller is designed (denoted LQG

), using

the weighting matrices

)10,10diag(





R and

)4000,5000,80,50,80,20,1,1,1,1diag(



Q . The

observer weightings are chosen as

)1.0,1.0,10,10diag(



W

and

BBV





with

10



Another LQG controller (denoted LQG

) which

uses additional information from the accelerometers

is next developed. This increases the initial

robustness of the controller. The poles of the closed-

loop obtained with LQG

are presented in Fig. 5.

Secondly, the initial MPC (denoted MPC0) is

designed with the following tuning parameters:

),,,diag( ,14N,58N,8

00u21

JJJ

RRRN 





10,10diag





R ,



,,diag

JJJ

QQQ 



30,30,30,80,1,1,1,1diag



Q .

Figure 5: Closed-loop LQG

poles.

The MPC controller uses the information of both

angular positions and accelerations of the Pivot and

C-arc.

Thirdly, two robustified controllers are further

developed:

RMPC0 that considers only robust stability

under additive unstructured uncertainties,

obtained from MPC0 with the Q parameter

which is the solution of (20);

RMPC1 that takes into account robust stability

under both additive and multiplicative

unstructured uncertainties. This robustified

controller is obtained from MPC0 coupled with

the Q parameter from (22). The coefficients

50 and 1



cc are used in the optimization

problem (22).

In both cases the degree of the Q polynomial is

chosen equal to

10

. The weighting

W (Fig. 3)

on the control increment is chosen as a high-pass

filter

05.0/)95.01(

1

 zW

and the weighting

(Fig. 4) is chosen as 1.0/)9.01(

1

 zW

, in

order to favor the high frequency range. The total

number of scalar decision variables associated with

the LMI problem (20) is 948 and with the LMI

optimisation problem (22) is 1387.

5.2 Frequency Analysis

In the case of a multivariable system, the classical

criteria for the analysis of stability margins such as

the Nyquist criterion are no longer valid. This is the

main reason why an analysis of the maximal

singular values, which can give a meaningful

assessment of the robustness of the controlled

system, is further proposed.

In a first stage, the maximal singular values of

the transfer from

b to u obtained with the LQG

ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

295

controller that uses only the motor shaft positions

(LQG

) and for the LQG with additional

measurements of the joints accelerations (LQG

) are

illustrated in Fig. 6. A significant improvement of

the controlled system behavior with the LQG

controller can be noticed at the high frequency

range. Thus the LQG

controller is kept for further

comparisons with MPC0, RMPC0 and RMPC1. For

simplicity reason the LQG

controller is further

denoted LQG.

Figure 6: Maximal singular values for the transfer from b

to u.

Figure 7: Maximal singular values for the transfer from b

to u.

In a second stage, a comparative analysis of the

maximal singular values from b to u is offered in

Fig. 7. The



H norm of transfer

T (which is the

maximum of the maximal singular values) is

progressively decreased from LQG to MPC0 and

then to RMPC0. The MPC and the robustified MPC

controllers have better frequency responses in the

high frequency range than the LQG controller. The

robustified controller RMPC1 offers a good trade-

off in terms of



H norm between MPC0 and

RMPC0.

From the analysis of the maximal singular values

of the complementary sensitivity function depicted

in Fig. 8, the LQG controller has the largest

bandwidth leading to a better behavior in the time

domain. The



H norm of the transfer

is very

similar for all the considered controllers.

Figure 8: Maximal singular values of the complementary

sensitivity function.

5.3 Time Domain Comparison

The time domain responses are obtained using a step

set-point of magnitude

1.0





rad for the pivot

and

15.0







rad for the C-arc. A step

disturbance of magnitude 200Nm at time 2s on both

axes was also considered.

Figure 9 presents the outputs

q of the

nonlinear model of the 2 axes of the robot. All the

controllers offer good tracking, a time response

without overshoot (which is imposed by the demand

specifications) and an admissible disturbance

rejection. The time responses are very similar for all

the controllers (

s72.0



rPivot

t and s62.0

rCarc

t ).

The LQG controller offers the fastest disturbances

rejection. The disturbances rejection is slower after

robustification, which was expected due to the

frequency domain behavior. In fact the Youla-

Kučera parameter will improve the robust stability

under additive uncertainties and will slow down the

disturbances rejection. The controller RMPC1 offers

a good trade-off between the considered controllers

(see the corresponding zoom of Fig. 9).

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

296

Figure 9: Output

q – Motor shaft positions comparison.

Figure 10 shows the control signals applied on

the nonlinear model. All the controllers offer

admissible control signals that can be implemented

on the real robot. A small oscillation (which could

come from numerical problems) can be seen on the

LQG controller.

Figure 10: Control signals – Motor torques comparison.

The robust synthesis algorithms, usually offer

large controllers. In this case the Youla-Kučera

parameter increases the dimension of the RMPC1

controller with 20 states. In order to reduce the

controller states a balanced reduction of the Youla-

Kučera parameter based on the Hankel singular

values is considered. The final controller (denoted

RMPC1r) uses a reduced Youla-Kučera parameter

that has only 4 states. Figure 11 illustrates the

singular values of the Youla-Kučera parameter

before and after the order reduction.

Figure 11: Singular values of Youla parameter before and

after order reduction.

The influence of an unstable transmission zero

(determining the behavior at the beginning of the

simulation) over the pivot axis can be easily noticed

in Fig. 9 and Fig. 10. The existence of this unstable

zero explains the choice of the prediction horizons

114N,18

N .

A robust analysis of the results is also proposed.

The aim is to verify the stability of the controllers

with the nonlinear model, considering structured

uncertainties on the joint stiffness

and motor

inertia

J . Only RMPC1 and RMPC1r remain

stable for all the considered parameters variations as

synthesised in Table 1, where the following

notations have been used:

Case 1: KK %20



;

Case 2: KK %20



;

Case 3:

JJ %20



;

Case 4:

JJ %20



ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

297

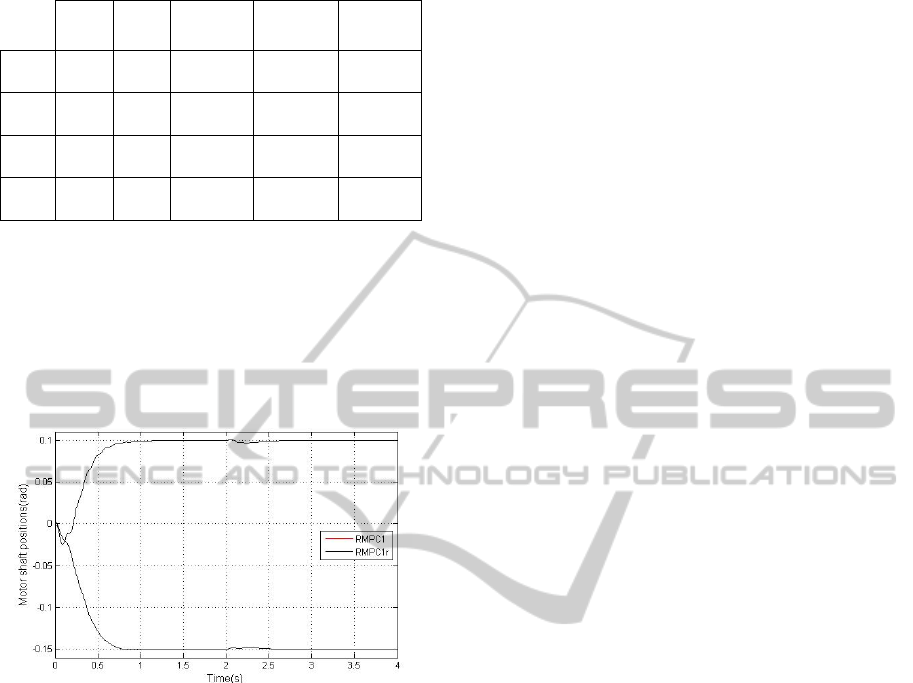
Table 1: Structured uncertainties robustness.

LQG MPC RMPC0 RMPC1

RMPC1r

Case 1     

Case 2     

Case 3     

Case 4     

Figure 12 illustrates the case where an

uncertainty of

%20 is considered on the motors

inertia:

JJ %20 . Despite this uncertainty and

the nonlinearities of the system, the robustified

controller RMPC1 still stabilises the system.

Moreover, it can be observed that this property is

conserved even after the order reduction.

Figure 12: Output

q . Nonlinear model with

uncertainties of

JJ %20

6 CONCLUSIONS

This paper proposes a comparison between

advanced control techniques for the control of the

angular position of a two axes model of a

cardiovascular robot, which is a strongly nonlinear

multivariable system. In order to improve the

controllers’ robustness, several layers of

robustification are further considered.

A linear quadratic controller (LQG) and a Model

Predictiv Control (MPC) law are first designed to

achieve similar level of performance for the time-

domain response. In a first step, additional

measurements of the joints accelerations are used in

order to increase the initial level of robustness of the

two controllers. Robust stability under unstructured

uncertainties is explicitly considered in the synthesis

of the robustified MPC controllers, while, for the

LQG controller, the robust stability under

unstructured uncertainties is verified a posteriori.

Simulation results show a trade-off between robust

stability and disturbances rejection.

The robustness towards the variation of some

parameters (i.e. structured uncertainties) is verified a

posteriori for all the considered controllers. An

interesting perspective is to take into account these

structured uncertainties during the synthesis of the

robustified MPC. A possibility is to consider a

polytopic uncertain domain around the nominal

model as in (Stoica et al., 2009) and to guarantee the

stability over the specified uncertain polytopic

domain solving a BMI (Biliniar Matrix Inequality)

optimisation problem.

REFERENCES

Al Assad, O., Godoy, E., Croulard, V., 2008. Macroscopic

drive chain efficiency modeling using state machines.

17th IFAC World Congress, Seoul, pp. 2294-2299.

Al Assad, O., Godoy, E., Croulard, V., 2007.

Irreversibility modeling applied to the control of

complex robotic drive chains. 4th ICINCO, Angers,

pp. 217-222.

Book, W. J., 1989. Modelling, design, and control of

flexible manipulators arms: status and trends. NASA

Conference on Space Telerobotics, vol. 3, pp. 11-24.

Boyd, S., Barratt, C., 1991. Linear controller design.

Limits of performance, Prentice Hall.

Boyd, S., Ghaoui, L. El., Feron, E., Balakrishnan, V.,

1994. Linear matrix inequalities in system and control

theory, SIAM Publications, Philadelphia.

Camacho, E. F., Bordons, C., 2004. Model predictive

control, Springer-Verlag. London, 2

edition.

Clement, B., Duc, G., 2000. A multiobjective control via

Youla parameterization and LMI optimization:

application to a flexible arm, IFAC Symposium on

Robust Control and Design, Prague.

Doyle, J. C., Stein, G., 1979. Robustness with observers.

In IEEE Trans. Automatic Control, vol. AC 24, pp.

607-611.

Halalchi, H., Bara, G. I., Laroche E., 2010. LPV controller

design for robot manipulators based on augmented

LMI conditions with structural constraints, IFAC

Symposium on System, Structure and Control, Ancona,

Italy.

Hedjar R., Toumi, R., Boucher, P., Dumur, D., 2002.

Feedback nonlinear predictive control of rigid link

robot manipulators, IEEE ACC, Anchorage, AK,

USA, pp. 3594-3599.

Kučera, V., 1974. Closed loop stability of discrete linear

single variable systems, Kybernetika, vol. 10(2),

pp. 146-171.

Maalouf, A.I., 2006. Improving the robustness of a

parallel robot using Predictive Functional Control

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

298

(PFC) tools, 45th IEEE CDC, San Diego, CA, USA

pp. 6468-6473.

Maciejowski, J. M., 2001. Predictive control with

constrains, Prentice Hall.

Maciejowski, J. M., 1989. Multivariable feedback design,

Addison-Wesley Publishing Company, Wokingham.

Merabet, A, Gu, J., 2009. Generalized predictive control

for single-link flexible joint robot, International

Journal on Sciences and Techniques of Automatic

Control, vol. 3, no. 1, pp. 890-899.

Moreno-Valenzuela, J., Santibáñez, V., Campa, R., 2008.

On output feedback tracking control of robot

manipulators with bounded torque input, International

Journal of Control, Automation, and Systems, vol. 6,

no. 1, pp. 76-85.

Sciavicco, L., Siciliano, B., 1996. Modelling and control

of robot. McGraw-Hill Company, Inc., New York.

Scherer, C. W., 2000. An efficient solution to multi-

objective control problem with LMI objectives.

Systems and Control Letters, 40, pp 43-57.

Spong, M. W., Hutchinson, S., Vidyasagar, M., 2005.

Robot modeling and control, John Wiley Sons Inc.,

2005.

Spong, M. W., 1992. On the robust control of robot

manipulators, IEEE Transactions on Automatic

Control, vol. 37, pp. 1782-1786.

Stoica, C., Rodríguez-Ayerbe, P., Dumur, D. 2007.

Improved robustness of multivariable Model

Predictive Control under model uncertainties, 4th

ICINCO, Angers, France, pp. 283-288.

Stoica, C., Al Assad, O., Rodriguez-Ayerbe, P., Godoy, E.

Dumur, D., 2009. Control of a flexible arm by means

of robustified MPC, European Control Conference,

Budapest, Hungary, pp. 2229-2234.

Tomei, P., 1994. Tracking control of flexible joint robots

with uncertain parameters and disturbances, IEEE

Transactions on Automatic Control, vol. 39, no. 5, pp.

1067-1072.

Youla, D. C., Jabr, H. A., Bongiorno Jr., J.J., 1976.

Modern Wiener-Hopf design of optimal controllers –

part II : the multivariable case, IEEE Transactions on

Automatic Control, vol. 21(3), pp. 319-338.

ROBUSTIFIED CONTROL OF A MULTIVARIABLE ROBOT

299