
COMPUTATIONAL EXPERIENCE WITH
STRUCTURE-PRESERVING HAMILTONIAN SOLVERS
IN OPTIMAL CONTROL
Vasile Sima
National Institute for Research & Development in Informatics, 8-10 Bd. Mares¸al Averescu, Bucharest, Romania
Keywords:
Linear-quadratic optimization, Optimal control, Structure-preserving algorithms.
Abstract:
Structure-preserving techniques for solving essential computational problems in optimal control are presented.
The techniques use possibly extended skew-Hamiltonian/Hamiltonian matrix pencils, and specialized algo-
rithms to exploit their structure: the symplectic URV decomposition, periodic QZ algorithm, solution of peri-
odic Sylvester-like equations, etc. The structure-preserving approach has the potential to avoid the numerical
difficulties which are encountered for a traditional, non-structured solution, returned by the currently available
software tools. Preliminary computational results are presented.
1 INTRODUCTION
Several basic computational problems in optimal and
robust systems analysis and design involve struc-
tured, e.g., Hamiltonian and symplectic, matrix pen-
cils. Two important problems, with many applica-
tions, are discussed below. One such basic computa-
tion is the evaluation of the L
∞
- and H
∞
-norms, which
are used, e.g., to quantify the trade-off between per-
formance and robust stability. Quadratically conver-
gent algorithms (Boyd et al., 1989; Bruinsma and
Steinbuch, 1990) for the computation of the these
norms use the purely imaginary eigenvalues of a ma-
trix or matrix pencil at each iteration. This matrix
(pencil) is structured, Hamiltonian or symplectic, in
the continuous- and discrete-time case, respectively.
(Actually, the pencils arising in the continuous-time
descriptor case are skew-Hamiltonian/Hamiltonian.)
Some details are given in (Sima, 2006) (and the ref-
erences therein), where the Hamiltonian structure is
exploited in the matrix case. The state-of-the-art func-
tion
norm
in the MATLAB
R
Control System Toolbox
computes the eigenvalues using the standard eigen-
solver
eig
, which does not take the structure into ac-
count. But the detection of purely imaginary eigenval-
ues is a delicate numerical problem if a non-structured
algorithm is used. Several simple examples are given
in Section 3.
Another fundamental computation in control sys-
tems design is the solution of continuous-time and
discrete-time algebraic Riccati equations(CAREs and
DAREs). CAREs and DAREs arise in many ap-
plications, such as, stabilization and linear-quadratic
regulator problems, Kalman filtering, LQG—linear-
quadratic Gaussian (H
2
-) optimal control problems,
computation of (sub)optimal H
∞
controllers, etc. In
applications, usually the stabilizing solution is re-
quired, which can be used to stabilize the closed-loop
system matrix or matrix pencil. A very important
class of CARE/DARE solvers makes use of stable
invariant or deflating subspaces of some matrices or
pencils, assuming certain nonsingularity and eigen-
value dichotomy assumptions (Laub, 1979; Pappas
et al., 1980). The associated CARE/DARE solvers
used matrix inversions (for instance, of the con-
trol weighting matrix, or of the system matrix, for
DAREs), but this can sometimes ruin the accuracy of
the results. Better results are obtained using stable
deflating subspaces of extended matrix pencils, with
no inversion involved (Bender and Laub, 1987a; Ben-
der and Laub, 1987b; Lancaster and Rodman, 1995;
Mehrmann, 1991; Sima, 1996; Van Dooren, 1981):
– extended pencil for CARE:
N −λM =
A 0 B
Q A
H
L
L
H
B
H
R
−λ
E 0 0
0 −E
H
0
0 0 0
;
– extended pencil for DARE:
N −λM =
A 0 B
Q −E
H
L
L
H
0 R
−λ
E 0 0
0 −A
H
0
0 −B
H
0
91
Sima V..
COMPUTATIONAL EXPERIENCE WITH STRUCTURE-PRESERVING HAMILTONIAN SOLVERS IN OPTIMAL CONTROL.
DOI: 10.5220/0003534100910096
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 91-96
ISBN: 978-989-8425-74-4
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

where A, E,Q ∈C
n×n
, B, L ∈ C
n×m
, R ∈ C
m×m
, Q =
Q
H
, R = R
H
. If
U
T
1
U
T
2
U
T
3
T
spans the sta-
ble right deflating subspace of N −λM, then the sta-
bilizing solution of the corresponding algebraic Ric-
cati equation is X
∗
= U
2
(EU
1
)
−1
(if E is nonsingular).
The solvers currently available, e.g., in MATLAB
R
Control System Toolbox, and SLICOT (Benner et al.,
1999; Benner et al., 2010), are using the standard QZ
algorithm for reordering the eigenvalues, to determine
the stable deflating subspaces. The special structure
of the matrix pencils involved is not exploited. But
the use of structure-preserving algorithms might im-
prove the numerical properties of the Riccati solvers.
Recently, structure-exploiting techniques have
been investigated for solving skew-Hamiltonian/
Hamiltonian eigenproblems, see, e.g., (Benner et al.,
2002; Benner et al., 2007). These techniques can be
employed for CARE solvers. For solving DAREs,
the pencils can be preprocessed by an extended Cay-
ley transformation, which only involves matrix addi-
tions and subtractions (Xu, 2006), to obtain equiva-
lent skew-Hamiltonian/Hamiltonian pencils.
The paper presents some preliminary results ob-
tained by the author using new software, devel-
oped in cooperation with Technical University Chem-
nitz, for computing the eigenvalues and stable deflat-
ing subspaces (with application in solving CAREs)
based on structure-exploiting algorithms for skew-
Hamiltonian/Hamiltonian matrix pencils. To the au-
thor’s knowledge, this is the first attempt to use such
algorithms in Riccati solvers.
This section is finished with few definitions. A
matrix pencil N −λM is Hamiltonian if NJ M
H
=
−MJ N
H
, and it is symplectic if NJ N
H
= MJ M
H
,
where
J :=
0 I
n
−I
n
0
, J
T
= −J = J
−1
,
the superscripts H and T denote the conjugate-
transpose and transpose, respectively, and I
n
denotes
the identity matrix of order n. If M = I
2n
, defini-
tions for Hamiltonian and symplectic matrices are ob-
tained; for instance, N is Hamiltonian if (NJ )
H
= NJ ,
and it is skew-Hamiltonian if (NJ )
H
= −NJ . A ma-
trix pencil λM −N is skew-Hamiltonian/Hamiltonian
if M is skew-Hamiltonian, and N is Hamiltonian.
These pencils have spectra which are symmetric with
respect to the imaginary axis. In the sequel, the pen-
cils λM −N will be represented in the numerically
better form αM −βN, with λ = α/β (possibly ∞).
2 COMPUTATION OF
EIGENVALUES AND STABLE
DEFLATING SUBSPACES
Let αS −βH be skew-Hamiltonian/Hamiltonian, i.e.,
(S J )
H
= −S J , (H J )
H
= H J . By definition, these
pencils have evensize. After eventualextension (to an
even size, 2(n+ℓ)), permutation and scaling, the pen-
cils corresponding to CARE have the following form
αS −βH = α
E 0 0 0
0 0 0 0
0 0 E
H
0
0 0 0 0
−β
A B
1
0 B
2
L
H
2
R
H
12
B
H
2
R
22
−Q −L
1
−A
H
−L
2
−L
H
1
−R
11
−B
H
1
−R
12
, (1)
where the four block rows and columns have or-
ders n, ℓ, n, and ℓ, respectively. For some prob-
lems, including linear-quadratic optimization applica-
tions, S can be given in a factored form, the so-called
skew-Hamiltonian Cholesky factorization, defined by
S = J Z
H
J
T
Z (with the blocks of J of order n + ℓ).
For instance, in (1),
Z =
I
n
0 0 0
0 I
ℓ
0 0
0 0 E
H
0
0 0 0 0
.
Some properties of skew-Hamiltonian/Hamilto-
nian pencils are proven, e.g., in (Benner et al., 2002).
For convenience, the real case only is dealt with in
the sequel. An algorithm for computing the eigenval-
ues and a basis for the stable right deflating subspace
(corresponding to the eigenvalues with strictly neg-
ative real part) of a skew-Hamiltonian/Hamiltonian
pencil is summarized below, based on Algorithm 4
in (Benner et al., 2007):
1. Compute the following decompositions, defined
by the matrices Q
1
and Q
2
,
Q
T
1
S J Q
1
J
T
=
N
1
N
2
0 N
T
1
,
(J Q
2
J
T
)
T
S Q
2
=
M
1
M
2
0 M
T
1
,
Q
T
1
H Q
2
=
H
11
H
12
0 H
22
,
where N
1
, M
1
, and H
11
are upper triangular, N
2
=
−N
T
2
, M
2
= −M
T
2
, and H
T
22
is upper quasi-triangular.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
92

2. Find orthogonal matrices Q
3
and Q
4
, such that
N
11
= Q
T
4
N
1
0
0 M
1
Q
3
,
H
11
= Q
T
4
0 H
11
−H
T
22
0
Q
3
,
where N
11
is upper triangular, and H
11
is upper quasi-
triangular.
3. Update
N
12
= Q
T
4
N
2
0
0 M
2
Q
4
,
H
12
= Q
T
4
0 H
12
H
T
12
0
Q
4
,
and form
R
N
=
N
11
N
12
0 N
T
11
, R
H
=
H
11
H
12
0 −H
T
11
.
4. Determine an orthogonal matrix
b
Q , such that
J
b
Q
T
J
T
αR
N
−βR
H
b
Q is still in structured triangu-
lar form and Λ (R
H
,R
N
) is contained in the spec-
trum of the leading 2p × 2p principal subpencil of
αN
11
−βH
11
. The notation Λ (N,M) denotes the sta-
ble spectrum of the pencil αM−βN, and p is the num-
ber of eigenvalues in Λ (H ,S ).
5. Set
V =
I
2n
0
Y
J Q
1
J
T
0
0 Q
2
P
×
Q
3
0
0 Q
4
b
Q
I
2p
0
,
where
Y =
√
2
2
I
2n
I
2n
−I
2n
I
2n
, P =
I
n
0 0 0
0 0 I
n
0
0 I
n
0 0
0 0 0 I
n
,
and compute an orthogonal basis of the stable deflat-
ing subspace.
Step 2 of the algorithm needs to reorder the eigen-
values in the formal matrix product
N
−1
1
H
11
M
−1
1
H
T
22
, (2)
where H
T
22
is upper quasi-triangular, and all the other
matrices are upper triangular, so that the triangular
form is kept, but the last diagonal blocks correspond
to all nonpositive real eigenvalues and the first di-
agonal blocks correspond to the other eigenvalues.
Note that Step 1 also uses the formal matrix prod-
uct in (2), to reduce the obtained upper Hessenberg
matrix H
T
22
to upper quasi-triangular form, while pre-
serving the other factors upper triangular. The peri-
odic QZ algorithm (Bojanczyk et al., 1992; Sreed-
har and Van Dooren, 1994) is used. Techniques for
eigenvalue reordering in formal matrix products are
discussed in (Sima, 2010) and the references therein.
Solutions of certain periodic Sylvester-like equations
are used. No factor is actually inverted. If only the
eigenvalues are desired, they are returned by the peri-
odic QZ algorithm called in Step 1 of the algorithm.
The structure can be exploited in Step 3 of the al-
gorithm. For instance, N
12
= −N
T
12
and H
12
= H
T
12
,
and so, only their upper triangular parts should be
computed. Also, the first block row only of the matri-
ces R
N
and R
H
can be used in Step 4.
The reordering involved in Step 4 does not need
the periodic QZ algorithm, but the standard QZ al-
gorithm, for upper block triangular pencils of order
3 or 4. (Actually, the second matrix of the small or-
der pencils is upper triangular.) In addition, reorder-
ing of the eigenvalues of special 2 ×2 or 4 ×4 skew-
Hamiltonian/Hamiltonian pencils is needed. This can
be done using relatively simple matrix calculations,
as well as the QR factorization, and Givens rotations.
A similar algorithm for a factored matrix S is sum-
marized in (Sima, 2010), based on Algorithm 3 in
(Benner et al., 2007), and the called algorithms. In
this case, the formal matrix product involves six fac-
tors. Moreover, the computations begin with an ini-
tial reduction, called generalized symplectic URV de-
composition, defined as follows (Benner et al., 2007):
Given a real 2n ×2n skew-Hamiltonian/Hamiltonian
pencil αS −βH , S = T Z (T = J Z
T
J
T
), orthogonal
matrices Q
1
, Q
2
and orthogonal symplectic matrices
U
1
, U
2
are determined, such that
Q
T
1
T U
1
=
T
11
T
12
0 T
22
,
U
T
2
Z Q
2
=
Z
11
Z
12
0 Z
22
,
Q
T
1
H Q
2
=
H
11
H
12
0 H
22
,
where T
11
, T
T
22
, Z
11
, Z
T
22
, and H
11
are upper triangular,
and H
T
22
is upper quasi-triangular. By definition, the
matrices U
i
, i = 1,2, have the following form,
U
i
=
U
i1
U
i2
−U
i2
U
i1
,
so, they can be stored compactly in an implementation
(the first n rows only).
Below is a summary about the related software:
• Fortran and MATLAB software for eigenvalues and
deflating subspaces have just been developed.
COMPUTATIONAL EXPERIENCE WITH STRUCTURE-PRESERVING HAMILTONIAN SOLVERS IN OPTIMAL
CONTROL
93

• Both real and complex cases are considered.
• Factored or unfactored versions are covered.
• Optimized kernels for problems of order 2, 3, or 4,
called by the general solvers, are available.
3 NUMERICAL RESULTS
This section presents some preliminary numerical re-
sults. These results have been obtained on a portable
Intel Dual Core computer at 2 GHz, with 2 GB
RAM, and relative machine precision ε ≈ 2.22 ×
10
−16
, using Windows XP (Service Pack 2) operat-
ing system, Intel Visual Fortran 11.1 compiler, and
MATLAB 7.11.0.584 (R2010b).
3.1 Computation of Eigenvalues
Many numerical tests have been performed, to assess
the correct behavior of the developed solvers. The
matrices
S =
A D
E A
T
, H =
B V
W −B
T
,
where A, B, D, E, V, W ∈ R
m×m
, have been gener-
ated with MATLAB commands using either uniform
(0,1) random generator or the normal random gen-
erator, so that D and E be skew-symmetric matrices
and V and W be symmetric matrices, resulting skew-
Hamiltonian/Hamiltonian pencils.
Few very small skew-Hamiltonian/Hamiltonian
examples are used below to illustrate the limita-
tions of the standard, non-structured approach. The
generalized eigenvalues computed by a structure-
preserving algorithm and the standard QZ algorithm,
optimally implemented in the MATLAB function
eig
,
have been compared with those delivered by sym-
bolic calculations, using the following MATLAB com-
mands
1
Ss = sym( S ); Hs = sym( H );
evs = double( eig( Ss \ Hs ) );
It was not possible to symbolically solve problems
with m ≥ 5. Based on the symmetry properties of
the eigenvalues of the (H ,S ) pencils, just eigenvalues
with real parts larger than or equal to 0, and, for purely
imaginary eigenvalues, those with positive imaginary
parts, are reported. For instance, with
1
Unfortunately, there is no MATLAB generalized sym-
bolic eigensolver, so the
mldivide
(or
mrdivide
) operator
has been used, but the condition numbers of the tried skew-
Hamiltonian matrices were very small, with one exception,
for which S was singular.
S =
47 86 0 17
31 92 −17 0
0 −10 47 31
10 0 86 92
,
H =
2 86 88 15
10 69 15 2
15 67 −2 −10
67 95 −86 −69
,
the structured algorithm found the eigenvalues
0.483611677311569, 1.310473800979598ı
the MATLAB function
eig
returned
0.4836116773115708,
2.140945364757078·10
−15
+ 1.310473800979599ı
and the symbolic MATLAB function
eig
computed
0.4836116773115688, 1.310473800979598ı
where ı denotes the purely imaginary unit. The rela-
tive error norms of the first two solvers, compared to
the symbolic solver, have the values 1.19·10
−16
and
2.33 ·10
−15
, respectively. The first value is about 20
times smaller than the second one.
Fig. 1 and Fig. 2 show a comparison between the
eigenvalues computed by the factored version of the
structured algorithm and the standard algorithm
eig
for two examples of order 4 (m = 2).
−3 −2 −1 0 1
x 10
−13
−100
−50
0
50
100
Real axis
Imaginary axis
Eigenvalues found by eig and structured algorithm
eig
str−alg
Figure 1: Eigenvalue scatter plot for an example of order 4.
For larger matrices, the differences between the
results produced by the structured solver and by
eig
were more pronounced. An example of order 8 had
two eigenvalues with real parts of order 10
−10
, and
an example of order 14 had two eigenvalues with real
parts of order 10
−8
, while the structured solver cor-
rectly found zero real parts for those eigenvalues.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
94

−2 −1.5 −1 −0.5 0
x 10
−11
−1000
−500
0
500
1000
Real axis
Imaginary axis
Eigenvalues found by eig and structured algorithm
eig
str−alg
Figure 2: Eigenvalue scatter plot for another example of or-
der 4. Two eigenvalues computed by
eig
are close between
them and close to the corresponding eigenvalues computed
by the structured solver.
3.2 Computation of Right Deflating
Subspaces
Thousands of tests have been performed with random
matrices for computing right deflating subspaces of
skew-Hamiltonian/Hamiltonian matrix pencils. The
results computed by the structured solver have been
in good agreement to those obtained by the stan-
dard solver. In addition, the solvers have been com-
pared for example problems from the SLICOT CARE
benchmark collection (Abels and Benner, 1999).
Most of them are difficult numerical examples. Three
alternativeoptions have been used for orthogonalizing
the subspace basis—QR factorization (QR, for short),
QR factorization with column pivoting (QRP), and
singular valuedecomposition(SVD). The results have
been compared with those delivered by the MATLAB
function
care
.
Table 1 defines the parameters of the CARE exam-
ples. The codification of the column “parameter” is as
follows: a value of -1 means that the default parame-
ter value(s) are used (see (Abels and Benner, 1999));
a value of 1 means that the other parameter value(s)
defined in (Abels and Benner, 1999) are used; a value
0 means that there are no parameters.
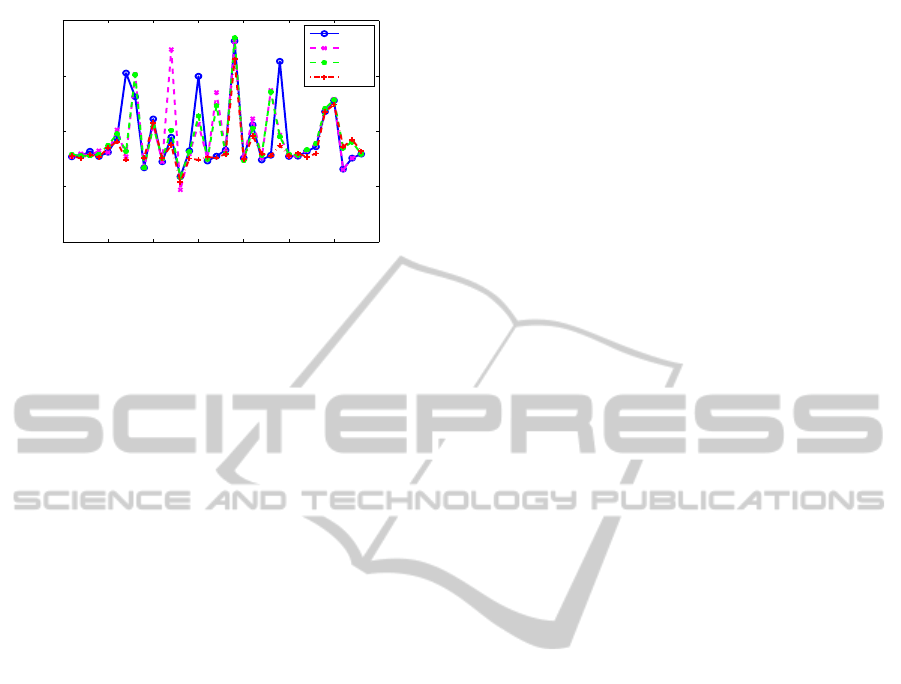
Fig. 3 presents the relative errors of the structured
CARE solver for the three orthogonalizing options:
QR, QRP, and SVD. The errors are relative to the ex-
act solution, when known, or to the solution returned
by the MATLAB function
care
, otherwise. Fig. 4
presents the relative residuals of the structured CARE
solver and
care
. The function
care
uses scaling and
permutations of the matrix or pencil, before reducing
it. The same scaling, but no permutation, was used by
the structured solver.
No orthogonalizing option is the best for all prob-
Table 1: CARE benchmark examples.
Test example n m parameter
1 1.1 2 1 0
2 1.2 2 1 0
3 1.3 4 2 0
4 1.4 8 2 0
5 1.5 9 3 0
6 1.6 30 3 0
7 2.1 2 1 1
8 2.1 2 1 -1
9 2.2 2 2 1
10 2.2 2 2 -1
11 2.3 2 1 1
12 2.3 2 1 -1
13 2.3 2 1 10
−6
14 2.4 2 2 1
15 2.4 2 2 -1
16 2.5 2 1 1
17 2.5 2 1 -1
18 2.6 3 3 1
19 2.6 3 3 -1
20 2.7 4 1 1
21 2.7 4 1 -1
22 2.8 4 1 1
23 2.8 4 1 -1
24 2.9 55 2 -1
25 3.1 9 5 1
26 3.1 39 20 -1
27 3.2 8 8 1
28 3.2 64 64 -1
29 4.1 21 1 -1
30 4.1 21 1 1
31 4.2 20 1 1
32 4.2 100 1 -1
33 4.3 60 2 -1
lems. Most examples are solved very well, but the re-
sults for some problems are not good enough. A pos-
sible explanation might be the fact that the structured
algorithm for computing the stable deflating subspace
doubles the eigenvalue multiplicities. Further investi-
gation is needed.
0 5 10 15 20 25 30 35
10
−20
10
−15
10
−10
10
−5
10
0
10
5
Test #
Relative errors
Relative errors for structured CARE solver
QR
QRP
SVD
Figure 3: Relative errors of the structured CARE solver for
CARE benchmark examples.
COMPUTATIONAL EXPERIENCE WITH STRUCTURE-PRESERVING HAMILTONIAN SOLVERS IN OPTIMAL
CONTROL
95
0 5 10 15 20 25 30 35
10
−30
10
−20
10
−10
10
0
10
10
Test #
Relative residuals
Relative residuals for CARE solvers
QR
QRP
SVD
care
Figure 4: Relative residuals of CARE solvers for CARE
benchmark examples.
4 CONCLUSIONS
Main issues related to the structure-preserving al-
gorithms for solving some essential control prob-
lems in optimal and robust systems analysis and de-
sign are summarized. Eigenvalues and stable right
deflating subspaces are computed based on skew-
Hamiltonian/Hamiltonian pencils. The results for
eigenvalue computations, with applications, e.g., in
evaluating L
∞
- and H
∞
-norms, are very good. The
computation of stable deflating subspaces, with ap-
plications in CARE/DARE solvers, deserves further
investigation for difficult numerical problems.
ACKNOWLEDGEMENTS
The work was partially supported by the German Re-
search Foundation (DFG) and The MathWorks, Inc.
The collaboration with Peter Benner and Matthias
Voigt from TU Chemnitz is highly acknowledged.
REFERENCES
Abels, J. and Benner, P. (1999). CAREX—A collection
of benchmark examples for continuous-time algebraic
Riccati equations (Version 2.0). SLICOT Working
Note 1999-14. http://www.slicot.org/.
Bender, D. J. and Laub, A. J. (1987a). The linear-quadratic
optimal regulator for descriptor systems. IEEE Trans.
Automat. Contr., AC-32(8):672–688.
Bender, D. J. and Laub, A. J. (1987b). The linear-quadratic
optimal regulator for descriptor systems: Discrete-
time case. Automatica, 23(1):71–85.
Benner, P., Byers, R., Losse, P., Mehrmann, V., and
Xu, H. (2007). Numerical solution of real skew-
Hamiltonian/Hamiltonian eigenproblems. Technical
report, Technische Universit¨at Chemnitz, Chemnitz.
Benner, P., Byers, R., Mehrmann, V., and Xu, H. (2002).
Numerical computation of deflating subspaces of
skew Hamiltonian/Hamiltonian pencils. SIAM J. Ma-
trix Anal. Appl., 24(1):165–190.
Benner, P., Kressner, D., Sima, V., and Varga, A.
(2010). Die SLICOT-Toolboxen f¨ur Matlab. at—
Automatisierungstechnik, 58(1):15–25.
Benner, P., Mehrmann, V., Sima, V., Van Huffel, S., and
Varga, A. (1999). SLICOT — A subroutine library in
systems and control theory. In Applied and Compu-
tational Control, Signals, and Circuits, vol. 1, ch. 10,
499–539. Birkh¨auser, Boston.
Bojanczyk, A. W., Golub, G., and Van Dooren, P. (1992).
The periodic Schur decomposition: algorithms and
applications. In Proc. of the SPIE Conference,
vol. 1770, 31–42.
Boyd, S., Balakrishnan, V., and Kabamba, P. (1989). A bi-
section method for computing the H
∞
norm of a trans-
fer matrix and related problems. Mathematics of Con-
trol, Signals, and Systems, 2(3):207–219.
Bruinsma, N. A. and Steinbuch, M. (1990). A fast algo-
rithm to compute the H
∞
-norm of a transfer function.
Systems & Control Letters, 14:287–293.
Lancaster, P. and Rodman, L. (1995). The Algebraic Riccati
Equation. Oxford University Press, Oxford.
Laub, A. J. (1979). A Schur method for solving algebraic
Riccati equations. IEEE Trans. Automat. Contr., AC–
24(6):913–921.
MATLAB (2010). The MATLAB Control System Toolbox.
Version 9.0.
Mehrmann, V. (1991). The Autonomous Linear Quadratic
Control Problem. Theory and Numerical Solution,
volume 163 of Lect. Notes in Control and Information
Sciences. Springer-Verlag, Berlin.
Pappas, T., Laub, A. J., and Sandell, N. R. (1980). On
the numerical solution of the discrete-time algebraic
Riccati equation. IEEE Trans. Automat. Contr., AC–
25(4):631–641.
Sima, V. (1996). Algorithms for Linear-Quadratic Opti-
mization. Marcel Dekker, Inc., New York.
Sima, V. (2006). Efficient algorithm for L
∞
-norm calcu-
lations. In 5th IFAC Symposium on Robust Control
Design, July 5–7, 2006, Toulouse, France.
Sima, V. (2010). Structure-preserving computation of stable
deflating subspaces. In Proceedings of the 10th IFAC
Workshop “Adaptation and Learning in Control and
Signal Processing”, Antalya, Turkey, 26–28 August
2010 — Kudret Press & Digital Printing Co.
Sreedhar, J. and Van Dooren, P. (1994). Periodic Schur form
and some matrix equations. In Proc. of the Symposium
on the Mathematical Theory of Networks and Systems,
vol. 1, 339–362, Regensburg, Germany.
Van Dooren, P. (1981). A generalized eigenvalue approach
for solving Riccati equations. SIAM J. Sci. Stat. Com-
put., 2(2):121–135.
Xu, H. (2006). On equivalence of pencils from discrete-time
and continuous-time control. Lin. Alg. Appl., 414:97–
124.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
96
