ON THE LIMIT BEHAVIOR OF MULTI-AGENT SYSTEMS
Ionela Prodan, Sorin Olaru, Cristina Stoica
SUPELEC Systems Sciences (E3S) - Automatic Control Department, 3 rue Joliot Curie, 91190 Gif-sur-Yvette, France
Silviu-Iulian Niculescu
Laboratory of Signals and Systems, CNRS-SUPELEC, 3 rue Joliot Curie, 91190, Gif-sur-Yvette, France
Keywords:
Linear quadratic (LQ) optimal controller, Model predictive control (MPC), Multi-agent systems.
Abstract:
This paper addresses the optimal control of multiple (linear) agents in the presence of a set of adversary con-
straints which makes the convergence towards the ”zero” relative position an infeasible task. By consequence,
this fixed point of the relative dynamics is replaced by a set of fixed points with different basin of attraction or
even by limit cycles. The present analysis is based on the existence of an optimum control law over a receding
horizon with one step ahead constraint. The feasible explicit solution in terms of a piecewise affine control
law is analyzed in order to characterize the limit behavior of an agent.
1 INTRODUCTION
Collision avoidance plays an important role in the
context of managing multiple agents. In the same
time it is known to be a difficult problem, since certain
constraints are non-convex.
The goal of the present paper is to describe the
limit behavior for an agent in the presence of adver-
sary constraints. More precisely, the agent state tra-
jectory has to avoid a convex region containing the
origin in its strict interior. This region can represent
an obstacle (static constraints) or another agent (dy-
namic constraints - leading in fact to a parametriza-
tion of the set of constraints with respect to the cur-
rent state). There are many applications which are of
particular interest to the present work, which include
either static or dynamic constraints. Examples for a
Mars rover which has to select feasible paths through
an obstacle field are presented in (Shiller, 2000). Re-
sults in the case of robots with full dynamics and mov-
ing along a given path avoiding stationary obstacles
are provided in (Bobrow et al., 1985). The behav-
ior analysis for an agent near a restricted region is
closely related to study the existence of fixed points
or limit cycles (see (Poincar´e and Magini, 1899)) and
their stability properties.
Our interest in these phenomena is originated by
the finite horizon formulation of Model Predictive
Control (MPC) technique including avoidance const-
straints for an agent. The first remark is that the pres-
ence of such constraints leads to the infeasibility of
the control law around the origin (which is an equi-
librium point for the autonomous system). This is
an unusual formulation for the classical MPC design.
To the best of the authors knowledge, all the studies
on constrained MPC rely on the assumption that the
origin is in the relative interior of the feasible region
(Mayne et al., 2000), (Seron et al., 2002), (Bemporad
et al., 2002) or on the frontier of the feasible region
(Pannocchia et al., 2003).
The main contribution of this paper is to provide a
description of the optimal solution of a constrained fi-
nite horizon optimization problem (originated by the
predictive control formulation). A simple algebraic
test can be formulated in order to verify the existence
of a stable equilibrium point with the basin of attrac-
tion equivalent to the entire feasible region. Alter-
natively, similar conditions can be formulated in or-
der to certify that the closed-loop behavior is unstable
over the entire feasible region. This last result can
be subsequently used for the design of unstable con-
trol laws (Chetaev, 1952) with the ultimate goal of
”repelling” the trajectories from a certain sensitive re-
gion of the state space. However these considerations
are out of the main topic of the present paper which
concentrates on the algebraic conditions for exclud-
ing limit cycles. The employed methods are specific
for Piecewise Affine (PWA) systems analysis, with a
344
Prodan I., Olaru S., Stoica C. and Niculescu S..
ON THE LIMIT BEHAVIOR OF MULTI-AGENT SYSTEMS.
DOI: 10.5220/0003535703440349
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 344-349
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

geometric insight on the invarianceproperties of poly-
topic regions in the state space.
The rest of the paper is organized as follows. In
Section 2 the constrained predictive control problem
is formulated. Section 3 considers the unbounded
interdicted region and analyzes the existence and
uniqueness of a fixed point on the frontier of the fea-
sible domain. Discussions based on the simulation re-
sults are presented in Section 4, while the conclusions
are drawn in Section 5.
The following notations will be used throughout
the paper. Denote B
n
p
= {x ∈ R
n
: kxk
p
≤ 1} as the
unit ball of norm p, where kxk
p
is the p-norm of vec-
tor x. The spectrum of a matrix M is the set of the
eigenvalues of M, denoted by Λ(M) = {λ
i
: i ∈ N} . A
point x
f
is a fixed point of a function f if and only if
f(x
f
) = x
f
(i.e. a point identical to its own image).
The boundary of a set S, denoted by ∂S is the set of
points which can be approached both from S and from
the outside of S.
2 PROBLEM STATEMENT
In the sequel, the principles of a receding horizoncon-
trol problem are recalled. Let us model the behavior
of an agent with a discrete time linear time-invariant
system:
x
k+1
= Ax
k
+ Bu
k
, (1)
where x
k
∈ R
n
is the state of the agent, u
k
∈ R
m
is
the input signal and A, B are matrices of appropriate
dimensions. It is assumed that the pair (A, B) is sta-
bilizable. The state constraints describe a polytopic
region S in the state-space:
S =

x ∈ R
n
:
˜
h
T
i
x ≤
˜
k
i
, i = 1 : n
h

, (2)
with (
˜
h
i
,
˜
k
i
) ∈ R
n
× R and n
h
the number of half-
spaces. This paper focuses on the case where
˜
k
i
> 0,
meaning that the origin is contained in the strict inte-
rior of the polytopic region, i.e. 0 ∈ S. The normaliza-
tion of the right hand side of the inequalities (2) leads
to
S =

x ∈ R
n
: h
T
i
x ≤ 1, i = 1 : n
h

, (3)
with h
i
=
˜
h
i
/
˜
k
i
∈ R
n
. Such limitations arise both from
for collision or obstacles avoidance problems. Note
that the feasible region in the solutions space is a non-
convex region defined as the complement R
n
\S. This
implies at the modeling stage a compact represen-
tation of the obstacles and/or a safety region for an
agent in terms of (3)
1
.
1
A safety region can be associated to each agent and im-
poses that the inter-agent dynamics do not overlap each in-
Let x
k+1|k
denote the value of x at time instant
k + 1, predicted upon the information available at
time k ∈ N. A finite receding horizon implemen-
tation of the optimal control law is typically based
on the real-time construction of a control sequence
u = {u
k|k
,u
k+1|k
,··· ,u
k+N−1|k
} that minimizes the fi-
nite horizon quadratic objective function:
u
∗
= arg
u
min(x
T
k+N|k
Px
k+N|k
+
N−1
∑
i=1
x
T
k+i|k
Qx
k+i|k
+
+
N−1
∑
i=0
u
T
k+i|k
Ru
k+i|k
) (4)
subject to:
(
x
k+i+1|k
= Ax
k+i|k
+ Bu
k+i|k
x
k+i|k
∈ R
n
\ S, i = 1 : N
Here Q = Q
T
 0, R ≻ 0 are positive definite weight-
ing matrices, P = P
T
 0 defines the terminal cost and
N denotes the prediction horizon.
It has to be mentioned that the solution of the un-
constrained finite horizon problem is the well-known
linear state-feedback control law:
u
k
= K
LQ
x
k
(5)
where K
LQ
is computed from the solution of the dis-
crete algebraic Riccati equation. Making the assump-
tion that the pair (A, B) is stabilizable, the stabilizing
LQ-optimal controller can be found before the res-
olution of the problem (4), closed-loop stability ex-
plicitly requiring that the state enters into a terminal
region (containing the origin) at the end of the predic-
tion horizon (Mayne et al., 2000). This considerations
do not fit the present framework as long as the equi-
librium point is not ”approachable”. Nevertheless, the
stability analysis is an important issue and it will be
one of the aims in the rest of the paper.
The objective is to find if the agent state either ap-
proaches a fixed point, or a periodic orbit (a ”limit cy-
cle”), or a finite set of fixed points. In a second stage
we will be interested in the description of the basin
of attraction and relate the analysis with classical sta-
bility results. For the sake of compactness, simplicity
of notation and representation, an analysis of second
order dynamical systems is proposed, i.e. the planar
case. It turns out that this situation is simple enough
to obtain useful results, and rich enough to gain some
understanding about the difficulties in higher dimen-
sions. Note that some of the 2-dimensional case argu-
ments from planar geometry will not longer be valid
in higher dimensions. Therefore, the generalization
for the n-dimensional case is still an open issue.
dividual restriction. It is important to assure that a control
action will not lead to a cycling behavior which implies en-
ergy consumption.
ON THE LIMIT BEHAVIOR OF MULTI-AGENT SYSTEMS
345

3 THE UNBOUNDED
RESTRICTED REGION
The half-spaces defining the frontier of the feasible
domain in (3) is considered. The LQ optimal con-
trol action is admitted as long as the trajectory does
not transpass the constraints. Otherwise, the con-
trol action is modified such that the constraint is ac-
tivated. Consequently, the explicit solution of an
one-step ahead receding horizon optimization prob-
lem (i.e. N = 1 in (4)) is analyzed, with the impli-
cations on the resulting autonomous agent dynamics.
Figure 1 describes the regions obtained through parti-
tioning with the imposed constraints, the hyperplane
of the restricted region and the explicit MPC parti-
tioning, respectively.
Consider the case of a single half-space, i.e n
h
=
1 in (3). The optimization problem to be solved is
formulated as follows:
u
∗
k
= arg
u
k
min(x
T
k+1
Px
k+1
+ u
T
k
Ru
k
), (6)
subject to:
(
x
k+1
= Ax
k
+ Bu
k
h
T
1
x
k+1
≥ 1
After introducing x
k+1
in the cost function and the in-
equality constraint, the optimization problem (6) is re-
formulated as follows:
u
∗
k
= arg
u
k
min(
1
2
u
T
k
(R+ B
T
PB)u
k
+ x
T
k
A
T
PBu
k
), (7)
subject to: − h
T
1
Bu
k
≤ −1+ h
T
1
Ax
k
.
The solution of (7) is a continuous piecewise affine
function of x, defined over a polyhedral partition
{C
j
}
j∈{0,1}
of C ⊆ R
2
satisfying C =
S
j∈{0,1}
C
j
and
for which C
0
∩C
1
have a relative empty intersection.
Explicitly, the solution of (7) is defined as:
u
∗
k
= F
j
x
k
+ G
j
, ∀ x
k
∈ C
j
and j ∈ {0,1}, (8)
where F
T
j
∈ R
2
, G
j
∈ R. As illustrated in Figure 1,
the polyhedral partitions {C
j
}
j∈{0,1}
are defined as:
C
0
= {x ∈ R
2
: h
T
c
x ≥ 1}, (9)
C
1
= {x ∈ R
2
: h
T
c
x < 1}, (10)
where h
c
∈ R
2
is given by the first-order Karush-
Kuhn-Tucker (KKT) optimality conditions (Bempo-
rad et al., 2002):
h
T
c
= h
T
1
(A−B(R+ B
T
PB)
−1
B
T
P
T
A
| {z }
K
LQ
). (11)
Let us consider
W =

x ∈ R
2
: h
T
1
x ≥ 1

, (12)
h
T
1
x = 1
(0,0)
h
T
c
x = 1
W =

x : h
T
1
x ≥ 1

S =

x : h
T
1
x < 1

X
1
= C
1
∩ W
X
0
= C
0
∩ W
Figure 1: Exemplification of the regions determined
by constraints.
where 0 /∈ W (from the definition of the restricted re-
gion (3), for the case n
h
= 1). Define X
0
, X
1
⊆ R
2
such that, X
0
= C
0
∩W denotes all the state trajecto-
ries fromW which under the LQ dynamics (5) remain
in W at the next iteration and X
1
= C
1
∩W denotes all
the state trajectories that at the next iteration transit in
the restricted region. The previous definitions can be
formally described as:
X
0
= {x ∈ R
2
: h
T
1
x ≥ 1, h
T
1
(A+ BK
LQ
)x ≥ 1}, (13)
X
1
= {x ∈ R
2
: h
T
1
x ≥ 1, h
T
1
(A+ BK
LQ
)x ≤ 1} (14)
with X
0
∪ X
1
= W.
Remark 1. One of the optimal solutions (8) corre-
sponds to the unconstrained optimum (5). Without
any loss of generality it is assumed to be for the par-
tition C
0
(i.e. the affine term is G
0
= 0).
Thereforethe closed-loop system can be described
by the following piecewise affine dynamics:
x
k+1
=
(
(A+ BK
LQ
)x
k
, for x
k
∈ X
0
(A+ BF
1
)x
k
+ BG
1
, for x
k
∈ X
1
(15)
Remark 2. The existence of the constraint in the op-
timization problem (7) makes the origin, which rep-
resents the fixed point for the dynamics associated to
the polyhedral set X
0
, to reside outside the validity
domain: 0 /∈ X
0
.
Proposition 1. Consider the system (1) with the con-
trol law defined by (8). The following statements are
verified:
a. All the state trajectories initiated in x
k
∈ X
0
transit
in a finite time to X
1
.
b. The dynamics associated to the polyhedral set X
1
defined by (15) will steer any point from X
1
in one
step on the boundary of the feasible region, i.e.
{x ∈ R
2
: h
T
1
x = 1}.
Proof: a. Consider x
k
∈ X
0
such that all the
future values under LQ dynamics (5) reside in X
0
.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
346

As (A+ BK
LQ
) is a Schur matrix it means that
for any ε ∈ R
∗
+
there exists a t
max
∈ N such that
||(A+ BK
LQ
)
t
max
x
k
|| < ε. But, Remark 2 states that
0 /∈ X
0
, therefore it follows that any x
k
has to transit
from X
0
in a finite time. From the definition of X
0
(13)
it follows that the transit set is X
1
, thus concluding the
proof.
b. Since inside the polyhedral set X
0
(defined in
(13)) the result of the optimization problem (6) corre-
sponds to the unconstrained optimum (5) due to the
fact that h
T
1
x
k+1
> 1, it follows that the polyhedral
set X
1
(14) corresponds to the constraint activation
h
T
1
x
k+1
= 1. As a consequence, for any x
k
∈ X
1
one
has x
k+1
on the boundary of the feasible region, thus
concluding the proof. 
Remark 3. Note that a consequence of Proposition
1.b is that one of the eigenvalues of the state matrix
associated to X
1
is 0 since the dynamics of X
1
repre-
sent a projection on a ”n− 1” dimensional set (i.e. on
∂S, with n
h
= 1).
Taking into account the above remarks, the forth-
coming study is concentratedon the polyhedralset X
1
.
In particular, the aim is to define simple mathematical
conditions for the existence and uniqueness of a stable
fixed point on the frontier of the feasible domain.
Therefore, the qualitativebehavior of the agent (1)
is determined by the pattern of its fixed points, as well
as by their stability properties. One issue of practical
importance is whether the fixed point x
f
associated
to the polyhedral region X
1
is stable or unstable and
whether x
f
is included in X
1
or X
0
.
The following theorem is stated as a main result
for defining simple and sufficient algebraic conditions
for the existence and uniqueness of a stable/attractive
fixed point of system (15).
Theorem 1. Consider the discrete-time system (1) in
closed-loop, with the optimal solution (8) of the opti-
mization problem (6).
If there existsV ∈ R
2×2
with nonnegativeelements
such that

−h
T
1
h
T
c

(A+ BF
1
) = V

−h
T
1
h
T
c

, (16)
and
(V − I)1 < −

−h
T
1
h
T
c

BG
1
, (17)
with h
c
defined by (11) and
F
1
= −G
1
h
T
1
h
c
− (R+ B
T
PB)
−1
B
T
PA,
G
1
= (R + B
T
PB)
−1
B
T
h
1
(h
T
1
B(R+ B
T
PB)
−1
B
T
h
1
)
−1
,
then we have the following properties with respect to
x
f
= (I − (A+ BF
1
))
−1
BG
1
:
a. If x
f
∈ X
1
, then x
f
is a unique stable fixed point
with a basin of attraction W defined by (12).
b. If x
f
/∈ X
1
, then the closed-loop dynamics are
globally unstable in W with x
f
an unstable fixed
point. Moreover, all the trajectories transit to in-
finity along the boundary of the feasible region.
Proof: The first-order Karush-Kuhn-Tucker
(KKT) optimality conditions (Bemporad et al., 2002)
provides the construction of F
1
and G
1
. Consider the
polyhedral set X
1
described as X
1
= C
1
∩ W, where
the set W defined in (12) is invariant with respect
to the piecewise affine dynamics (15) (the set W is
composed by two regions X
0
,X
1
, which do not tran-
sit outside the set, see Proposition 1). Using Lemma
1 (see Appendix) we prove that C
1
defined in (10) is
a positively invariant set with respect to the dynam-
ics x
k+1
= (A + BF
1
)x
k
+ BG
1
from (15). Therefore,
taking into account that the set X
1
is the intersection
between two invariant sets, results that X
1
is also a
positively invariant set.
a. Now, let us consider the case where the fixed
point x
f
is contained by the invariant set X
1
. Since the
dynamics x
k+1
= (A+ BF
1
)x
k
+ BG
1
associated to X
1
are affine, then the fixed point is:
- unique by the fact that over the frontier X
0
∩X
1
the
system dynamics correspond to the closed-loop
dynamics x
k+1
= (A + BK
LQ
)x
k
which admits a
unique fixed point on the origin. But 0 /∈ X
1
and
thus {1} /∈ Λ(A+ BF
1
).
- stable by the fact that the dynamics in X
1
contain
an eigenvalue at the origin (see Remark 3) while
the second eigenvalue is inside the unit disc as a
consequence of the invariance and continuity.
The local attractivity in X
1
is completed with the at-
tractivity in W = X
0
∪ X
1
as a consequence of Propo-
sition 1.
b. Let us consider the point z
k
∈ R
n
such that
z
k
∈ {x ∈ R
2
: h
T
1
x
k
= 1} ∩ {x ∈ R
2
: h
T
c
x
k
= 1},
(18)
with h
c
given by (11). In order to establish that in the
case where the affine dynamics of X
1
is unstable, all
the trajectories convergeto infinity, it suffices to prove
that all future values starting from z
k
as in (18) will
transit in X
1
on the boundary of the feasible region.
We prove this by contradiction.
Assume that z
k
will transit in one step in X
0
(i.e.
z
k+1
∈ X
0
). Since by its definition z
k
∈ X
1
it follows
from Proposition 1.b that z
k+1
is on the boundary of
the feasible region. Consequently we state the follow-
ing relations:
h
T
1
z
k
= 1, (19)
h
T
1
z
k+1
= h
T
1
A
LQ
z
k
= 1, (20)
where A
LQ
= A + BK
LQ
denotes the closed-loop dy-
namics of region X
0
. Consequently, at the next itera-
ON THE LIMIT BEHAVIOR OF MULTI-AGENT SYSTEMS
347

tion we have that
h
T
1
z
k+2
> 1. (21)
The Cayley-Hamilton theorem states that replacing
A
LQ
∈ R
2×2
in the characteristic polynomial yields to
A
2
LQ
+ c
1
A
LQ
+ c
2
I = 0, which is equivalent to
A
2
LQ
= −c
1
A
LQ
− c
2
I, (22)
with c
1
,c
2
∈ R and
c
1
+ c
2
< 1. (23)
Introducing (22) and (23) in (21) it results that
h
T
1
z
k+2
= h
T
1
(−c
1
A
LQ
− c
2
I)z
k
= −(c
1
+ c
2
).
We reach a contradiction as long as (21) is satisfied.
Subsequently, we have shown by contradiction that
z
k+1
∈ X
0
is false, therefore all future values starting
from z
k
will transit in X
1
.
Let there be V and Λ the Jordan decomposition
VΛV
−1
= A + BF
1
. Remark 3 states that one of the
eigenvalues of the state matrix is 0, allowing to write
the dynamics associated to the set X
1
:
x
k+1
= VΛV
−1
x
k
+ BG
1
. (24)
After elementary algebraic operations it results that

y
1
k+1
y
2
k+1

=

0
λ

y
1
k
y
2
k

+

δ
1
δ
2

, (25)
where y
k
=

y
1
k
y
2
k

= V
−1
x
k
,

δ
1
δ
2

= V
−1
BG
1
and λ is
the nonzero eigenvalue of Λ. After k iterations the
following relations are obtained:
y
1
k+1
= δ
1
(26)
y
2
k+1
= λ
k
y
2
0
+
k−1
∑
i=0
λ
i
δ
2
(27)
Using (27) we observe that as long as λ ≥ 1 the dis-
tance between x
f
and z
k
expands at the next iteration,
that is
||z
k
− x
f
|| = |λ| · kz
k+1
− x
f
k. (28)
In addition, if there exists V ∈ R
2×2
such that the con-
ditions (16), (17) are satisfied, X
1
is an invariant set.
Therefore, any point from W has a trajectory that di-
verges from x
f
(x
f
/∈ X
1
). Finally, it results that all
the trajectories transit to infinity along the boundary
of the feasible region. 
4 SIMULATION RESULTS
Consider an agent in two spatial dimensions with the
dynamics described by:
A = 0.9

cos(
π
4
) −sin(
π
4
)
sin(
π
4
) cos(
π
4
)

, B =

1
1

(29)
where [x y]
T
and u are the state and the input of the
agent, respectively. The components of the state are
the position coordinates of the agent. The pair (A, B)
is stabilizable. The tunning parameters of the opti-
mization problem (7) are
P =

1.32 0.08
0.08 2.32

, R = 1. (30)
a. Consider the set of state constraints as defined
in (3) with h
T
1
= [−0.1 0.01]
T
and n
h
= 1. Solv-
ing the optimization problem (7), an explicit solution
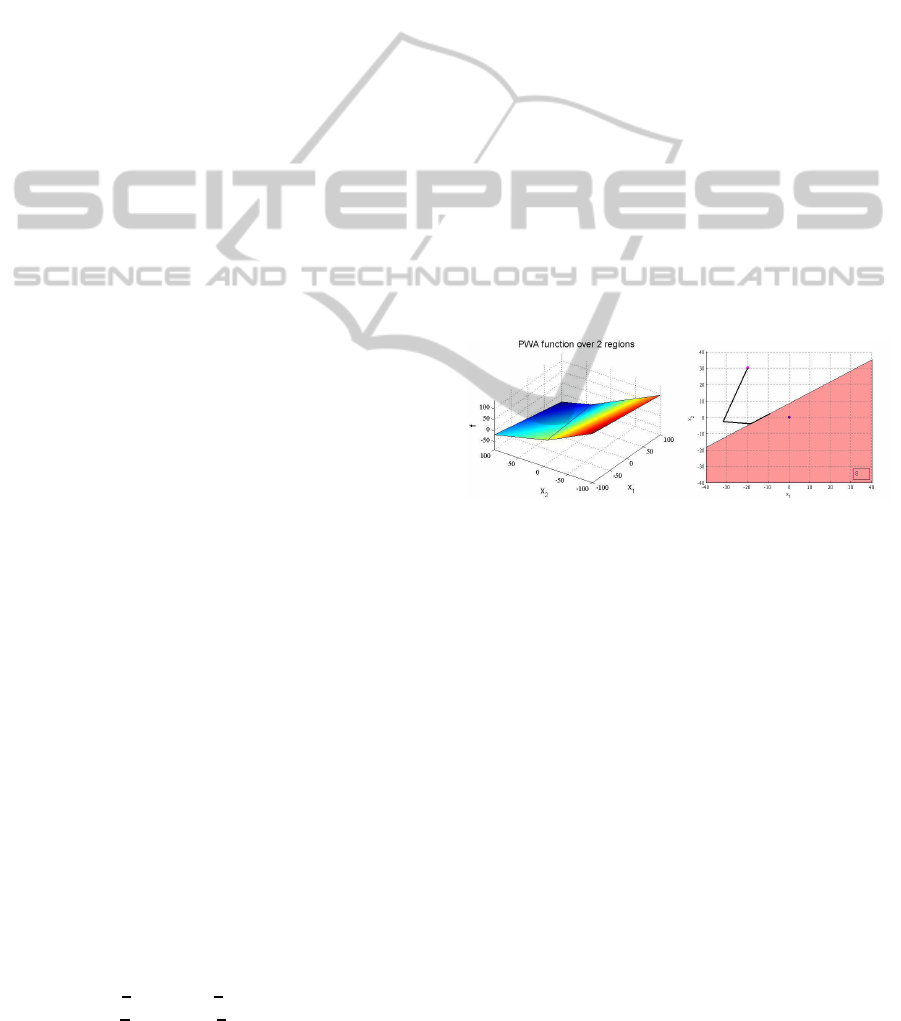
defined over two polyhedral regions is obtained (Fig-
ure 2.a). The optimization problem is feasible since
the agent trajectory satisfies the imposed constraints,
Figure 2.b. We obtained V =

0 0
0.16 0.8

such
that the algebraic conditions (16) and (17) defined in
Theorem 1 are verified. Figure 3.a depicts the re-
gion X
0
corresponding to the unconstrained control
action and the invariant set X
1
for which condition
the {x ∈ R
n
: h
T
1
x ≥ 1} is saturated. In this particu-
lar case, X
1
has a stable dynamics and contains the
associated stable fixed point x
f
= [−5.18 2.96]
T
.
(a) (b)
Figure 2: (a) The optimal explicit solution. (b) The evo-
lution of the agent state trajectory which satisfies the con-
straints described by the half-space.
b. Consider the set of state constraints as defined
in (3) with h
T
1
= [0.31 0.42]
T
and n
h
= 1. We
obtained V =

0 0
0.16 3.01

such that the alge-
braic conditions (16) and (17) defined in Theorem 1
are verified. Figure 3.b illustrates the region X
0
corresponding to the unconstrained control action
and the region X
1
corresponding to the saturation of
{x ∈ R
n
: h
T
1
x ≥ 1}. In this case, X
1
has an unsta-
ble dynamics and the associated unstable fixed point
x
f
= [14.05 −8.03]
T
is in X
0
. The conditions of The-
orem 1.b are fulfilled, therefore all the points transit
to infinity along the boundary of the feasible region,
Figure 3.b.
For any hyperplane tangent to the circle (Figure 3)
there existsV ∈ R
2×2
with nonnegative elements such
that (16) and (17) defined in Theorem 1 are verified.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
348

−40
−35
−30
−25
−20
−15
−10
−5
0
5
10
15
20
25
30
35
40
−40
−30
−20
−10
0
10
20
30
40
x
1
x
2
S
x
f
X
1
X
0
(a)
−40
−35
−30
−25
−20
−15
−10
−5
0
5
10
15
20
25
30
35
40
−40
−30
−20
−10
0
10
20
30
40
x
1
x
2
S
x
f
X
1
X
0
(b)
Figure 3: (a) Exemplification for the existence of a unique
stable fixed point on the boundary of the feasible region. (b)
Exemplification for the case where all the points transit to
infinity.
5 CONCLUSIONS
The paper presents and develops a set of conditions
for the optimality of a dynamic motion planning of
an agent in the presence of a set of adversary con-
straints. This type of constraints are unusual because
they make the agent trajectory converging to origin
to be infeasible. Since the origin is normally a sta-
ble point, these conditions may generate a limit cycle.
Consequently, simple algebraic conditions for the ex-
istence and uniqueness of a stable fixed point on the
boundary of the feasible region represent the main re-
sult of this paper.
ACKNOWLEDGEMENTS
The authors would like to thank anonymous review-
ers for their useful comments and remarks. The re-
search of Ionela Prodan is financially supported by
the EADS Corporate Foundation (091-AO09-1006).
REFERENCES
Bemporad, A., Morari, M., Dua, V., and Pistikopoulos, E.
(2002). The explicit linear quadratic regulator for con-
strained systems. Automatica, 38(1):3–20.
Bitsoris, G. (1988). On the positive invariance of polyhe-
dral sets for discrete-time systems. Systems & Control
Letters, 11(3):243–248.
Bobrow, J., Dubowsky, S., and Gibson, J. (1985). Time-
optimal control of robotic manipulators along speci-
fied paths. The International Journal of Robotics Re-
search, 4(3):3.
Chetaev, N. (1952). On the instability of equilibrium in
some cases where the force function is not maximum.
Prikl. Mat. Mekh, 16(1).
Mayne, D., Rawlings, J., Rao, C., and Scokaert, P. O.
(2000). Constrained model predictive control: Sta-
bility and optimality. Automatica, 36:789–814.
Pannocchia, G., Wright, S., and Rawlings, J. (2003). Ex-
istence and computation of infinite horizon model
predictive control with active steady-state input con-
straints. IEEE Transactions on Automatic Control,,
48(6):1002–1006.
Poincar´e, H. and Magini, R. (1899). Les m´ethodes nou-
velles de la m´ecanique c´eleste. Il Nuovo Cimento
(1895-1900), 10(1):128–130.
Seron, M., De Dona, J., and Goodwin, G. (2002). Global
analytical model predictive control with input con-
straints. In Proceedings of the 39th IEEE Conference
on Decision and Control, volume 1, pages 154–159,
Sydney, Australia.
Shiller, Z. (2000). Obstacle traversal for space explo-
ration. In Robotics and Automation, 2000. Proceed-
ings. ICRA’00. IEEE International Conference on,
volume 2, pages 989–994.
APPENDIX
Set Invariance
We use as an instrumental result the following lemma,
which is an adaptation for affine systems of the Propo-
sition 2 from (Bitsoris, 1988).
Lemma 1 . Consider the polyhedral set
Z(H, K) =

x ∈ R
n
: Hx ≤ K

,
with (H,K) ∈ R
r×n
×R
r
. If there existsV ∈ R
r×r
with
nonnegative elements such that
HΦ = VH and (31)
(V − I)K + HΓ ≤ 0, (32)
then Z(H,K) is a positively invariant set with respect
to the affine dynamics x
k+1
= Φx
k
+ Γ.
Proof: Suppose x
k
∈ Z. We want to prove that
x
k+1
∈ Z. By explicitly replacing
Hx
k+1
= H(Φx
k
+ Γ)
(31)
= VHx
k
+ HΓ,
and taking into account the hypothesis that Hx
k
≤ K
and V has nonnegative elements it follows that
Hx
k+1
≤ VK + HΓ.
with VK + HΓ = (V − I)K + HΓ+ K ≤ K which can
then be verified by (32). 
ON THE LIMIT BEHAVIOR OF MULTI-AGENT SYSTEMS
349