
BILATERAL CONTROL OF MASTER-SLAVE MANIPULATOR
SYSTEM USING TIME DELAY CONTROL
Jong Kwang Lee, Hyo Jik Lee, Byung Suk Park, Seung-Nam Yu, Kiho Kim and Ho Dong Kim
Fuel Cycle System Engineering Development Division, Korea Atomic Energy Research Institute, Daejeon, Korea
Keywords: Time delay control, Master-slave manipulator, Teleoperation.
Abstract: A prototype of dual arm master-slave manipulator system has been developed for use in a hot-cell at Korea
Atomic Energy Research Institute. The slave manipulator can handle a 25 kgf payload in any posture, where
the gravity force of remote tools or handling equipment has a great impact on the position error which
produces the unnecessary force that operator does not have to feel. In this work, we applied a time delay
controller for bilateral teleoperaiton of the manipulator system. Experimental results show that the time
delay controller has good performance of the position tracking as well as force reflection.
1 INTRODUCTION
The use of remotely operated manipulators and other
mechanical devices as replacements for human
workers in hazardous environment is a growing field
of research. In particular, master-slave manipulators
have been extensively used in the nuclear industries
governed by the ALARA principle for more than
five decades. The master manipulator is an input
device which interfaces with a human operator on
one side and with a slave manipulator on the other.
Bilateral force-reflecting control plays a key support
role in a successful dexterous manipulator for
master-slave manipulators. Great increases in the
performance of master-slave manipulator systems
can be achieved through a good design of the
mechanical hardware and a proper implementation
of the embedded control strategies.
Recently, we developed a prototype master-slave
manipulator system for integrated demonstration of
Pyroprocess which is a technology for refining
nuclear materials from spent nuclear fuels using an
electrochemical method in a molten salt bath at high
temperature (Lee, Park, Lee, Kim & Kim, 2010).
The Pyroprocess demonstration facility has a
completely sealed argon gas-filled cell, with
dimensions 40.3 × 4.8 × 6.4 m (L × W × H), where
direct access by human operators is not possible
during operation due to the high toxicity of argon
gas. Therefore, all the operation and maintenance of
process equipment must be performed remotely
through master-slave manipulation.
Position-based bilateral control of master-slave
manipulator system using PD controller has been
mainly applied in the real field teleoperation system
for practical reasons. However, the control
performance will be degraded in case of existence of
disturbances. In the controller, the position error
occurs significantly due to the change of the gravity
force of handling equipments. Therefore, it produces
unnecessary force reflected to an operator owing to
the nature of position error based force reflection.
To achieve a good tracking performance as well
as highly transparent control, we applied Time
Delay Control (TDC) for master-slave teleoperation.
TDC has been proposed as an effective control
method for nonlinear time-varying systems with
unknown dynamics and/or unpredictable
disturbances (Youcef-Toumi and Ito, 1990) and its
stability was proven by Youcef-Toumi (1992) and
Jung, Chang and Kang (2007). Hasia and Gao (1990)
applied TDC to robot position control. Chang, Kim
and Park (2004) used TDC to force/position control
for robot manipulator. Song and Byun (2000)
suggested a time delay controller with a variable
reference model to improve the transient response
characteristics and verified its performance on the
BLDC motor position control. Recently, to
overcome the performance degradation of the TDC
in presence of nonlinear friction, Han and Chang
(2010) proposed TDC with gradient estimator.
In this paper, we applied TDC to bilateral control
of master-slave teleoperation system and verified its
performance through experimental studies. This
37
Lee J., Lee H., Park B., Yu S., Kim K. and Kim H..
BILATERAL CONTROL OF MASTER-SLAVE MANIPULATOR SYSTEM USING TIME DELAY CONTROL.
DOI: 10.5220/0003535800370042
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 37-42
ISBN: 978-989-8425-75-1
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
paper is organized as follows. Section 2 describes a
prototype master-slave manipulator system and it
control system. TDC is introduced in section 3.
Section 4 illustrates experimental results of the TDC.
The conclusion is described in the final section.
2 TELEOPERATION SYSTEM
2.1 Master-slave Manipulator System
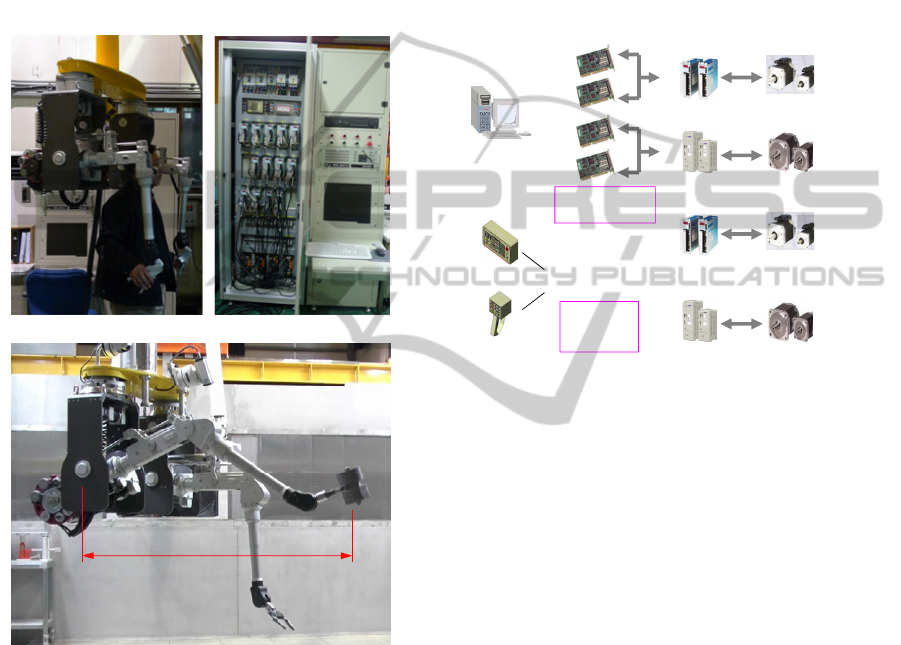
(a) master manipulator (b) control system
(c) slave manipulator
Figure 1: Master-slave teleoperation system.
Figure 1 shows a master-slave servo-manipulator
system, which have identical kinematic structures,
except for link lengths, drive system, and end-
effector type. Each arm of the master and the slave
manipulators was designed with a 6-DOF serial link
mechanism with all revolute joints, and power to
each joint is transmitted through a cable from a
corresponding motor mounted to a base frame. The
slave manipulator can hold a 25 kg object in any
pose, whereas the master manipulator reflects forces
of up to 5 kgf to the operator. To use the
teleoperation system, an operator manipulates the
master arm while viewing the equipment or objects
through an operating window or camera system.
2.2 Control System Hardware
Figure 2 shows configuration of the main control
system. It consists of a control PC, four 8-axes
motion control boards, motor drivers, a manual
console, a pendant, etc. Servo motors adopted in the
master-slave servo-manipulator are controlled by
using a torque control mode for realizing a bilateral
force reflection control.
Figure 2: Configuration of the motion control system.
A GUI operation program was written in Visual C++
6.0 and runs on Windows XP. This program displays
the status of the system, updates several control
parameters, and controls the transporter system. And
instead of the Windows timer function, which has a
somewhat unpredictable interval, we use a high-
precision multimedia timer callback function for
greater accuracy and resolution, achieving a control
update frequency of up to 1 kHz. This approach is
advantageous at the development stage because of
the ease of implementation and debugging.
3 REMOTE CONTROL
The master and slave manipulator have kinematically
identical structures, and so each pair arms can be
controlled by bilateral servo control without any
coordinate transformation. For achieving stable and
possibly transparent teleoperation, various
teleoperation control architectures such as position-
position control, position-force control, impedance
control, and compliant control have been proposed
(Aliaga, Rubio and Sánchez, 2004). However, in our
system, because of force/torque sensors cannot be
placed on the wrist of the slave manipulator, given
1.6 m
25 kgf
{
Motor
Drivers
Control
PC
Slave arm
(14 Axes)
Master arm
(14 Axes)
Slave
Transporter
(4 Axes)
Master
Transporter
(3 Axes)
{
JOG Mode
(velocity
control)
SERVO Mode
(torque control)
Manual console
Pendant
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
38
the high possibility for sensor failure and difficulties
in maintenance, the control architecture is
constrained to the use of only motor positions and
motor rates. For this reason, we have adopted
position-based bilateral force reflection controller
based on TDC. TDC uses recent past data to
estimate the uncertain dynamics and disturbances in
the system. It cancels out the undesired dynamics
and disturbances, and substitutes them with the
desired dynamics that given in terms of the reference
model. The controller design can be performed even
if the accurate model was not found. And modeling
error has little effect on the controller performance.
3.1 Time Delay Control Law
The dynamic equation of robot manipulator is given
by:
(
)
+
(
,
)
+
(
)
+
(
,
)
= (1)
where τ is the actuator torque; , and denote the
joint angle, joint angular velocity, and joint
acceleration, respectively. () is the inertia matrix;
(,) is the Coriolis and the centrifugal forces;
() is gravity force. (,) represents the friction
and unmodeled nonlinearities. In equation (1), let
() be approximated with
() as a constant
matrix, then the equation can be rewritten as
+
(
,,
)
= (2)
(
)
=(−
) +
(
,
)
+
(
)
+
(
,
)
(3)
Following the idea established by the computed
torque control approach, the control input is
computed as
=
+(,,) (4)
=
+
+
(5)
where
is the desired joint acceleration, =
−
,
and
are the derivative and the proportional
gain matrices, respectively. Substituting Equation
(4) and (5) into Equation (2), closed-loop error
equation can be obtained as follows:
+
+
=0 (6)
In the time delay control, it is usually assumed that
the value of the uncertainty at present time is very
close to its value at time − in past for a very
small time delay. Then, () can be estimated as
(
)
≈
(
−
)
=
(
−
)
−
(
−
)
. (7)
Combining equations (4), (5) and (7), the TDC law
is obtained as follows:
=
(
−
)
−
(
−
)
+
(
+
+
) (8)
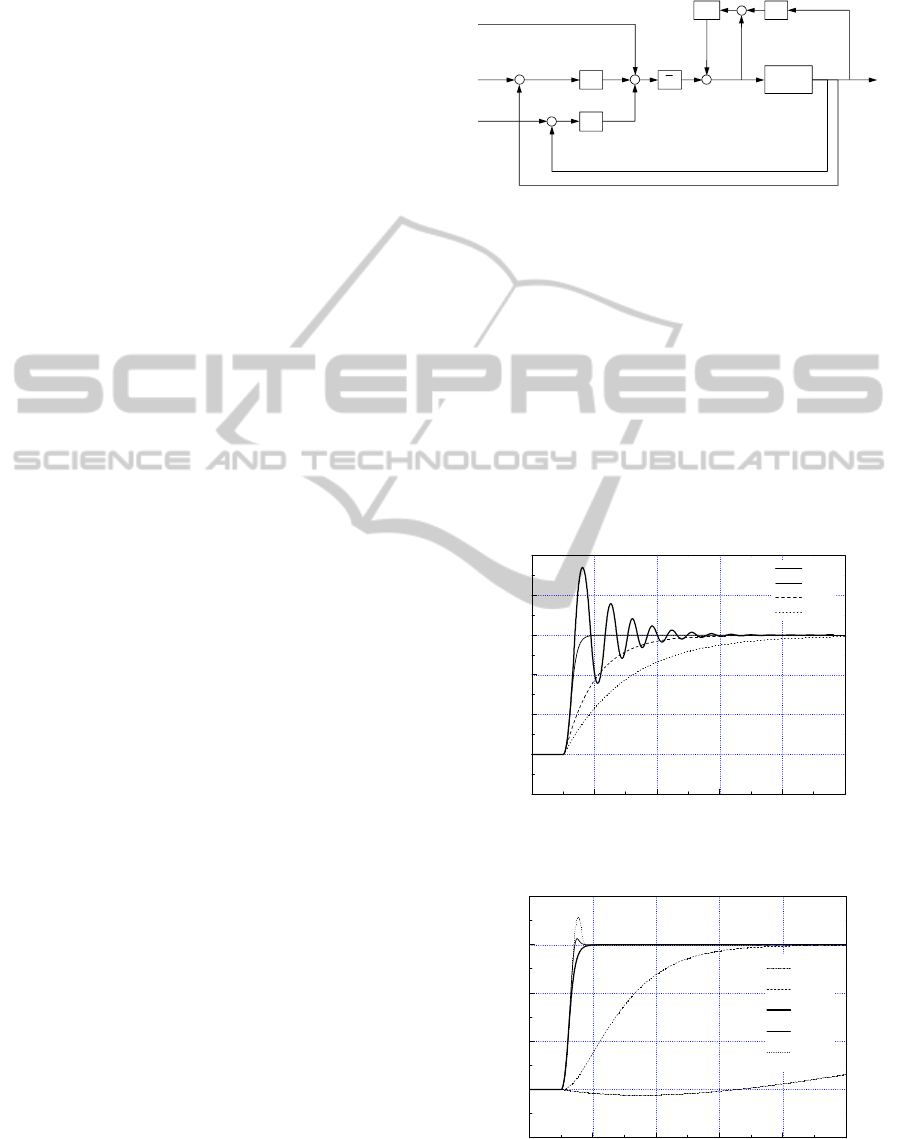
The structure of the controller is shown in Figure 3.
Figure 3: TDC block diagram.
The time delay is set as the sampling time of
the control system. Two PD-type gains,
and
,
can be determined from an error dynamics which
has a desired natural frequency
and a desired
damping ratio as
=
,
=2
(9)
Step responses of one link arm with variation of
and
, are shown in Figure 4 and 5, respectively.
Since these responses have typical characteristics of
second order system, the tuning procedure of the
TDC can be simple and straightforward.
Figure 4: Step responses of various .
Figure 5: Step responses of various
.
v
K
plant
p
K
d
q
d
q
d
q
q
q
q
M
L
s
e
−
+
−
+
−
+
+
+
+
+
−
+
τ
q
0246810
-20
0
20
40
60
80
100
Angle (deg)
Time (sec)
ζ=0.1
ζ=1
ζ=5
ζ=10
0246810
-20
0
20
40
60
80
Angle (deg)
Time (sec)
ω
n
=0.1
ω
n
=1
ω
n
=10
ω
n
=20
ω
n
=30
BILATERAL CONTROL OF MASTER-SLAVE MANIPULATOR SYSTEM USING TIME DELAY CONTROL
39
3.2 Controller Design for Master-slave
System
The dynamics of master and slave is given by the
following equations:
+
=
(
)
+
,
+
(
) (10)
−
=
(
)
+
,
+
(
) (11)
where
and
denote the position vector of
master and slave. and represent the inertia
matrix and the Coriolis and the centrifugal force
respectively. is the gravity vector.
is the force
that the operator applies to the master link and
denotes the force that the slave arm applied to the
object. Actuator driving forces are represented by
and
.
According to the TDC law, Eq.(10) and (11) are
rewritten in another form:
=
(
−
)
−
(
−
)
+
(
+k
+k
) (12)
=
(
−
)
−
(
−
)
+
(
+k
+k
) (13)
where
=
−
and
=
−
are position
errors of master and slave manipulators. And the
closed-loop error equation is
+
+
=0 (14)
+
+
=0 (15)
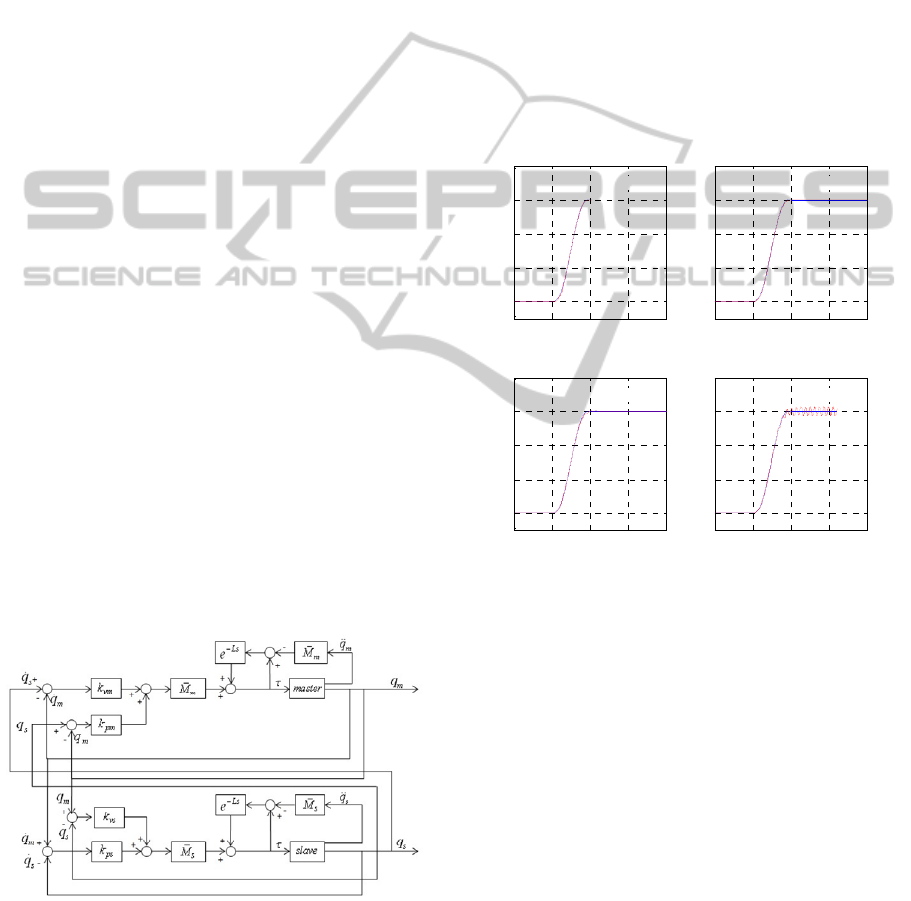
The structure of the master-slave control system
using TDC, is shown in Figure 6. Although it
represents simple one DOF model, it can be easily
extended to multi-DOF manipulator system since the
master-slave system is a replica type which enables
to apply a joint-to-joint control.
Figure 6: Master-slave control system with TDC.
4 EXPERIMENT
The developed master-slave system was tested to
determine its basic operating performance as well as
remote handling capability. The angular position of
the master-slave system was measured by counting
the encoder pulse signals. The angular velocity and
the angular acceleration were calculated by
numerical differentiation after passing them through
a low pass filter.
Figure 7 shows reference trajectory following
results with some TDC parameter variations. The
natural frequency and damping ratio of desired
response are set to be ω
=10 and ζ=1. M
in (8) could
be selected to satisfy the stability condition (Hsia
and Gao, 1990).
Figure 7: Reference trajectory following results with some
parameter variations.
The performances of the system with the TDC are
compared with those of the system with the PD. The
reference input is designed based on jerk-bounded
trajectory planning (Sonja and Elizabeth, 2003) and
it applied to both controllers with same values. The
gains of two controllers are same in all experiments.
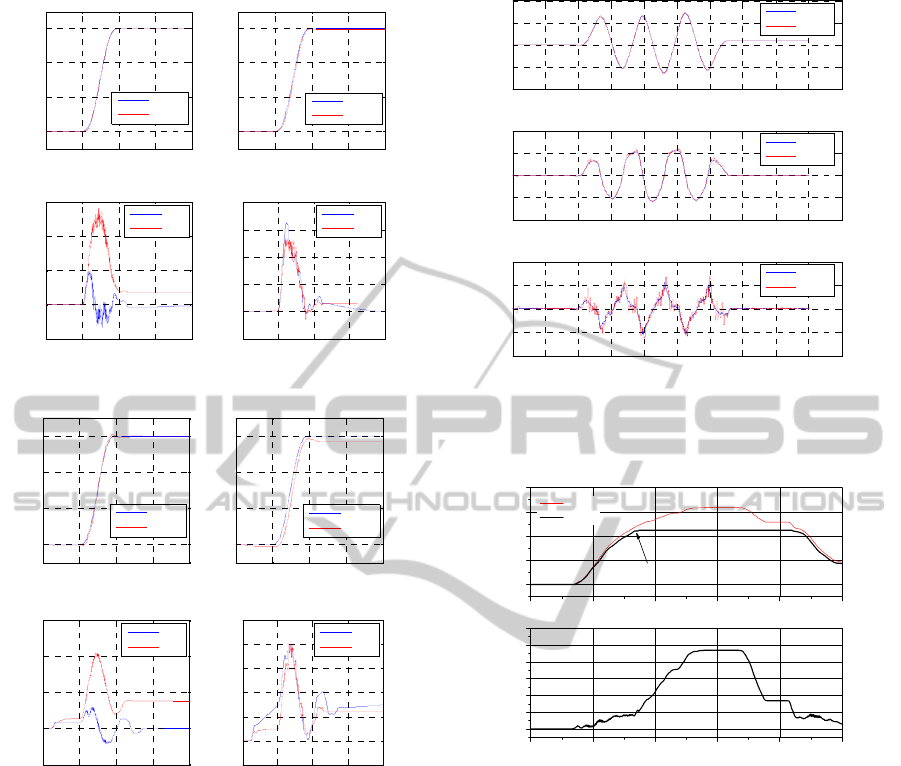
Figure 8 shows experimental results both with a
noload and with 25 kgf payload. The system with
PD controller has the steady-state error because the
controller has fixed gains and it cannot compensate
when the load changes or unpredictable disturbances
exist. Unlike PD controller, the TDC effectively
handles the effect of parameter variations and there
are no significant changes in the overall control
performance regardless of changes in payloads.
0 1 2 3 4
0
10
20
30
40
Mbar = 0.15
time (sec)
Angle (deg)
0 1 2 3 4
0
10
20
30
40
Mbar = 0.20
time (sec)
Angle (deg)
0 1 2 3 4
0
10
20
30
40
Mbar = 0.25
time (sec)
Angle (deg)
0 1 2 3 4
0
10
20
30
40
Mbar = 0.30
time (sec)
Angle (deg)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
40
(a) without payload
(b) with a payload of 25 kgf.
Figure 8: Comparison of the performance of PD and TDC.
Figure 9 illustrates a master-to-slave position
tracking performances along axis 1 during handling
a 10 kgf load. The three tracking indexes—position,
velocity, and acceleration—are quite similar across
both the master and slave manipulator even though
small errors and overshoot exist. However, an
operator could deal with these errors without
significant degradation since he is located in the
teleoperation loop.
Figure 10 shows a force feedback result when a
gripper is restricted by an obstacle during master-
slave operation. Instead of direct force measurement
of the master arm, we calculated the reflected force
through measuring the torque acting on its joints. In
the figure, we can see that an operator can feel the
contact with an environment.
Figure 9: Position tracking results during axis 1 motion
where the slave arm with a payload of 10 kgf follows
arbitrary motion of the master.
Figure 10: Position-based force reflection.
5 CONCLUSIONS
Time delay controller has been successfully
implemented for master-slave teleoperation system
and its performance was compared with that of the
conventional PD controller. From the experimental
results, TDC showed good performance in master
position tracking in spite of the changes in payload
and the force at slave site was effectively reflected to
the operator without additional force sensor.
Therefore, TDC is an efficient and applicable
bilateral force reflection scheme for the master-slave
servo-manipulation.
0 1 2 3 4
0
10
20
30
TDC
time (sec)
Angle (deg)
master
slave
0 1 2 3 4
0
10
20
30
PD
time (sec)
Angle (deg)
master
slave
0 1 2 3 4
-0.5
0
0.5
1
1.5
time (sec)
Tracking error (deg)
TDC
PD
0 1 2 3 4
-100
0
100
200
300
400
time (sec)
Output torque (Nm)
TDC
PD
0 1 2 3 4
0
10
20
30
TDC
time (sec)
Angle (deg)
master
slave
0 1 2 3 4
0
10
20
30
PD
time (sec)
Angle (deg)
master
slave
0 1 2 3 4
-2
0
2
4
6
time (sec)
Tracking error (deg)
TDC
PD
0 1 2 3 4
-200
0
200
400
600
800
1000
time (sec)
Output torque (Nm)
TDC
PD
0 2 4 6 8 10 12 14 16 18 20
-40
-20
0
20
40
time (sec)
Angle (deg)
master
slave
0 2 4 6 8 10 12 14 16 18 20
-100
-50
0
50
100
time (sec)
Vel. (deg/s)
master
slave
0 2 4 6 8 10 12 14 16 18 20
-400
-200
0
200
400
time (sec)
Acc. (deg/s
2
)
master
slave
0246810
0
1
2
3
4
5
6
Reflected force (N)
Time (sec)
0246810
0
10
20
30
40
slave
master
Angle (deg)
slave contacts to environment
BILATERAL CONTROL OF MASTER-SLAVE MANIPULATOR SYSTEM USING TIME DELAY CONTROL
41

ACKNOWLEDGEMENTS
This work was supported by Nuclear Research &
Development Program of National Research
Foundation of Korea (NRF) funded by Ministry of
Education, Science & Technology (MEST).
REFERENCES
Aliaga, I., Rubio, Á. & Sánchez, E. Inãki, A., Ángel, R.,
and Emilio, S. (2004). Experimental quantitative
comparison of different control architectures for
master-slave teleoperation. IEEE Trans. on Control
Systems Technology. 12(1): 2-11.
Chang, P. H., Kim, D. S. and Park, K. C. (1995). Robust
force/position control of a robot manipulator using
time-delay control. Control Engineering Practice, 3(9):
1255-1264.
Han, D. K. and Chang, P.-H. (2010). Robust tracking of
robot manipulator with nonlinear friction using time
delay control with gradient estimator. Joural of
Mechanical Science and Technology, 24(8): 1743-
1752.
Hsia, T. C. and Gao, L.S. (1990). Robot Manipulator
Control using Decentralized Linear Time-Invariant
Time-delayed Joint Controllers, IEEE Int. Conf. On
Robotics and Automation, 3:2070-2075.
Jung, J. H., Chang, P.-H. and Kang, S. H. (2007). Stability
analysis of discrete time delay control for nonlinear
systems. Proceeding American Control Conference,
5995-6002.
Lee, J. K., Park, B. S., Lee, H. J., Kim, K. and Kim, H. D.
(2010). Master-slave servo manipulator system for the
PRIDE facility. 1
st
Int. Conf. On Applied Robotics for
the Power Industry, 1-5.
Song, J.-B. and Byun, K.-S. (2000). Design of time delay
controller using variable reference model. Control
Engineering Practice, 8(5): 581-588.
Sonja, M. and Elizabeth A. C. (2003). Jerk-bounded
manipulator trajectory planning: design for real-time
application. IEEE Trans. on Robotics and Automation,
19(1): 42-52.
Youcef-Toumi, K. (1992). Robustness and stability
analysis of time delay control. American Control
Conference, 2691-2695.
Youcef-Toumi, K. and Ito, O. (1990). A time delay
controller for systems with unknown dynamics. ASME
J. Dynamic Systems Measurement and Control, 122:
904-911.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
42
