EFFICIENT RECONSTRUCTION OF UNIFORM SAMPLES FROM
BUNCHED NONUNIFORM SAMPLES
V. Harish, K. M. M. Prabhu
Department of Electrical Engineering, Indian Institute of Technology Madras, 600036 Chennai, India
Piet Sommen
Signal Processing Systems Group, Department of Electrical Engineering
Technical University Eindhoven, 5600 MB, Eindhoven, The Netherlands
Keywords:
Nyquist sampling rate, Bunched sampling, Recurrent nonuniform sampling, Uniform discrete Fourier trans-
form (DFT) filter bank.
Abstract:
In this paper, we derive a mathematically equivalent frequency-domain relation between uniform and bunched
nonuniform samples. This relation aids in the reconstruction of uniform samples, obtained from nonuniform
samples, using a uniform discrete Fourier transform (DFT) modulated filter bank. We consider a general case
of unequal spacing between the bunches of nonuniform samples. Simulation results demonstrate the practical
utility of the theory proposed.
1 INTRODUCTION
Shannon sampling theorem states that a signal ban-
dlimited to the frequencies [− f
0
, f
0
], can be recon-
structed perfectly from its samples taken uniformly at
no less than the Nyquist rate 2f
0
(Oppenheim et al.,
1999). This theorem also states that there will be dis-
tortion due to aliasing if the above condition is not
satisfied. In practice, there are situations in which the
reconstruction of the signal is required from nonuni-
form samples, say, due to channel erasures. How-
ever, it has potential applications, which include data
compression (Singh and Rajpal, 2007), speech cod-
ing, and error correcting codes (Marvasti, 2001). In
(Ouderaa and Renneboog, 1988), an exact nonuni-
form sampling scheme is proposed based on Cauchy’s
residue theorem, while a method for nonuniform sam-
pling based on amplitude of signals is proposed in
(Wang et al., 2004). There are various nonuniform
sampling techniques outlined in the literature (Jerri,
1977), (Marvasti, 2001), one of which is the periodic
or recurrent nonuniform sampling (Papoulis, 1977).
Recurrent nonuniform sampling finds an important
application in time interleaved analog-to-digital con-
verters (TI-ADCs) (Black and Hodges, 1980). The
time skews within the TI-ADCs produce recurrent
nonuniform samples. A digital signal processing ap-
proach is discussed in (Sommen and Janse, 2008),
which relates uniform samples and recurrent nonuni-
form samples using a uniform discrete Fourier trans-
form (DFT) modulated filter bank. In case of known
time skews, the reconstruction of uniform samples is
proposed in (Johansson and L¨owenborg, 2006) us-
ing a synthesis system composed of fractional delay
filters. However, in order to avoid the re-designing
of fractional delay filters, a slight over sampling of
bandlimited signal is considered in (Johansson and
L¨owenborg, 2006).
A near-perfect method of reconstructing uniform
samples from bunched samples has been proposed in
(Prendergast et al., 2004). In particular, the bunches
of uniform samples in (Prendergast et al., 2004) are
considered as equally spaced , which can be viewed
as a special case of recurrent nonuniform samples.
The proposed reconstruction technique in (Prender-
gast et al., 2004) uses least squares method. In this
paper, we propose a linear relation between uniform
samples and bunched nonuniform samples. But, un-
like in (Prendergast et al., 2004), we consider a gen-
eral case with unequal spacing between the bunches.
The linear relation proposed in this paper aids in per-
fect reconstruction of uniform samples from bunched
nonuniform samples.
One of the situations where bunched nonuniform
sampling occurs is in the context of lithographic ma-
chines. A lithographic machine is a robotic machine
350
Harish V., M. M. Prabhu K. and Sommen P..
EFFICIENT RECONSTRUCTION OF UNIFORM SAMPLES FROM BUNCHED NONUNIFORM SAMPLES.
DOI: 10.5220/0003537003500356
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 350-356
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

|
2
3
T
0
5
3
T
0
9
3
T
0
first bunch
δ
1
=
11
3
T
0
δ
2
=
12
3
T
0
δ
3
=
13
3
T
0
second bunch third bunch
|
time
Figure 1: Timing diagram of bunched nonuniform samples.
which apply patterns on wafers at high speeds. Dur-
ing the measurement on wafers, nonuniform expo-
sure parts of the movement profile produces bunched
nonuniform sampling patterns. This happens due to
missing data between the bunched samples. From
these bunched nonuniform samples, we require to
generate uniform samples. This paper is organized as
follows : In Section 2, we define bunched nonuniform
sampling scheme and present discrete time models for
the same. In Section 3, a frequency domain relation
between uniform and bunched nonuniform samples
is described. This section also deals with the recon-
struction of uniform samples from nonuniform sam-
ples. Section 4 presents the simulation results which
demonstrates the theory proposed and Section 5 con-
cludes the paper.
Notations Convention. In this paper, we follow the
notation conventions similar to those used in (Som-
men and Janse, 2008). Lower case letters for time
domain, upper case letters for frequency domain rep-
resentation of signals. Matrices, vectors are denoted
by boldface, underlined boldface letters, respectively;
[·]
T
denotes transpose, while diag {·} represents diag-
onal matrix.
2 BUNCHED NONUNIFORM
SAMPLING (BNU)
We consider recurrent frames of nonuniform sam-
ples, where the samples in each frame are grouped
into bunches. Precisely, bunches within a frame con-
tain equal number of samples, but these bunches are
not equally spaced. However, the number of sam-
ples within a frame satisfies the Nyquist rate. Fig-
ure 1 depicts a typical bunched nonuniform sam-
pling paradigm. In Fig. 1, we observe that one
recurrent frame of duration 12T
0
[s] contains three
bunches. Each bunch contains four nonuniform sam-
ples. In each bunch, the last three samples are sep-
arated by
2
3
T
0
,
5
3
T
0
, and
9
3
T
0
seconds from the first
sample. However, the time durations of the consec-
utive bunches are
11
3
T
0
,
12
3
T
0
, and
13
3
T
0
seconds, re-
spectively, and hence the gaps between consecutive
bunches are
2
3
T
0
,
3
3
T
0
, and
4
3
T
0
, respectively. It is
evident from Fig. 1 that the number of samples in
the frame satisfies the Nyquist criterion with
1
T
0
as
the Nyquist rate. Generally, a frame of M
1
M
2
T
0
[s]
contains M
2
bunches each containing M
1
samples.
Within a bunch, the consecutive samples are sepa-
rated by τ
1
T
0
,τ
2
T
0
,··· ,τ
M
1
−1
T
0
from the first sample
and we consider τ
0
= 0. The time durations of the
bunches are denoted by δ
1
T
0
, δ
2
T
0
, ·· · , δ
M
2
T
0
. To
analyze the bunched nonuniform sampling scheme,
we first consider the generation of bunched nonuni-
form samples of a bandlimited signal x(t). Without
of loss of generality, we assume the maximum fre-
quency of x(t) as
1
2T
0
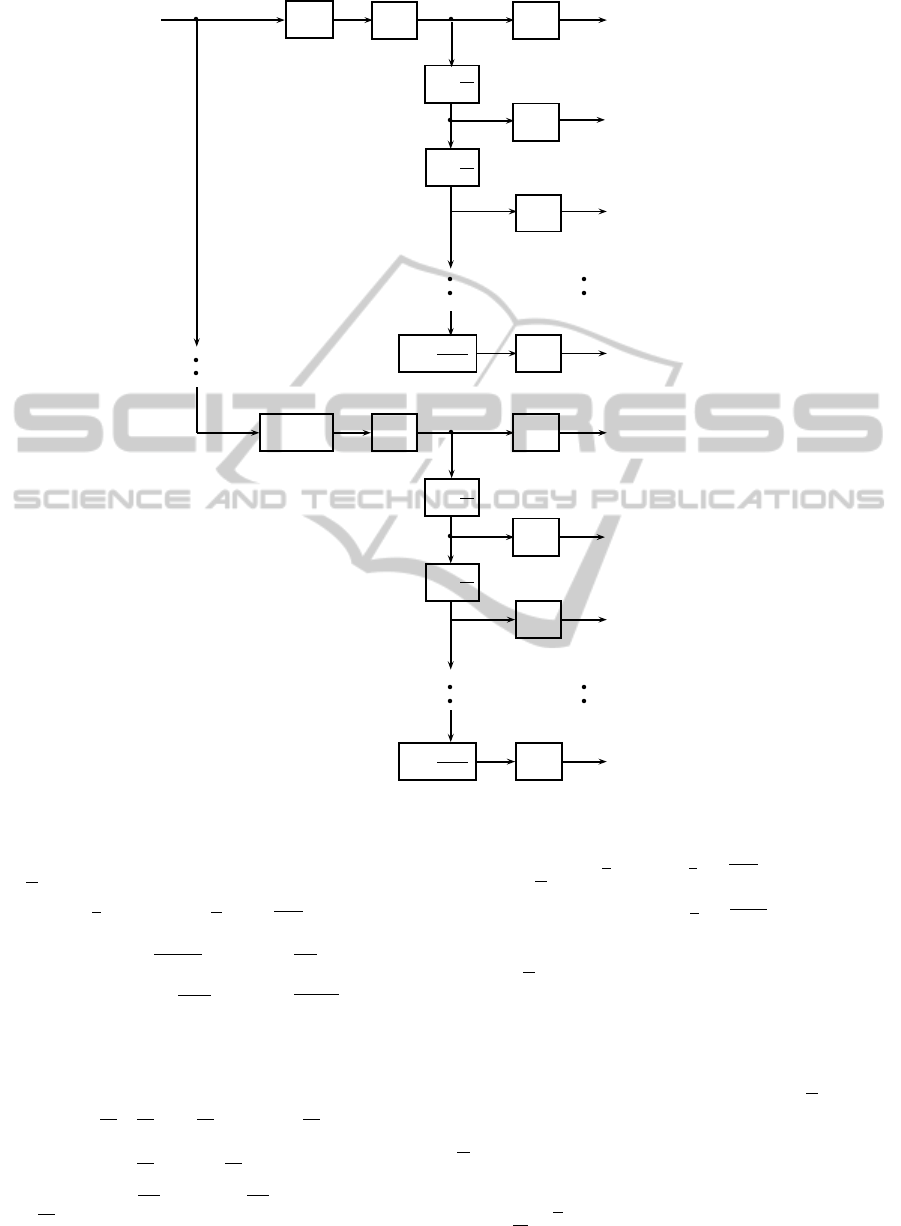
Hz. Figure 2 depicts a discrete
time model for the generation of bunched nonuniform
samples from uniform samples. In Fig. 2, the vari-
able θ denotes the digital frequency in radians. By as-
suming M = M
1
M
2
, we obtain an alternative discrete
time model (Sommen and Janse, 2008), which relates
uniform samples and bunched nonuniform samples as
shown in Fig. 3. In Fig. 3, the pairs of modulation and
demodulation terms are used to avoid phase jumps of
aliased signals after down sampling operation within
the fundamental interval θ ∈ [−π,π) (Sommen and
Janse, 2008). The delay elements in Figs. 2 and 3
are represented in the frequency domain with respect
to their corresponding sampling rates. In Fig. 3, the
frequency responses of the delays for the p-th branch
are defined as,
∆
s,p
(e
jθ
) = e
− jτ
p

θ−
M−1
M
π

, p = 0,1,· ·· ,M
1
− 1,
(1)
∆
k
s,p
(e
jθ
) = e
− j

θ−
M−1
M
·M
1
π

δ
k
M
1
, k = 1,2,·· · ,M
2
− 1.
(2)
3 FREQUENCY DOMAIN
RELATION BETWEEN
UNIFORM AND BUNCHED
NONUNIFORM SAMPLES
In this section, we provide a relation between uniform
and bunched nonuniform samples in the frequency
domain. With the help of alternative discrete time
model as well as Eqs. (1) and (2), we write,
Y
s
M× 1
(e
jθ
) =
1
M
· ∆(e
jθ
)
M× M
· W
M× M
· X
M× 1
(e
j
θ
M
)
(3)
where,
EFFICIENT RECONSTRUCTION OF UNIFORM SAMPLES FROM BUNCHED NONUNIFORM SAMPLES
351

x[n]
e
− jθτ
0
↓ M
1
↓ M
2
y
0
[m]
e
− jθ
δ
1
M
1
↓ M
2
y
1
[m]
e
− jθ
δ
2
M
1
e
− jθ
δ
M
2
−1
M
1
↓ M
2
↓ M
2
y
2
[m]
y
M
2
−1
[m]
e
− jθτ
M
1
−1
↓ M
1
↓ M
2
y
M
2
(M
1
−1)
[m]
e
− jθ
δ
1
M
1
↓ M
2
y
M
2
(M
1
−1)+1
[m]
e
− jθ
δ
2
M
1
y
M
2
(M
1
−1)+2
[m]
↓ M
2
↓ M
2
e
− jθ
δ
M
2
−1
M
1
y
M
1
M
2
−1
[m]
Figure 2: Discrete time model of bunched nonuniform sampling scheme.
Y
s
M×1
(e
jθ
) =
h
Y
s,0
(e
jθ
),··· ,Y
s,M−1
(e
jθ
)
i
T
(4)
∆
M×M
(e
j
θ
M
) = diag
n
e
− jθ
τ
0
M
,e
− jθ

τ
0
+δ
1
M

,
e
− jθ

τ
0
+δ
1
+δ
2
M

,··· , e
− jθ

τ
0
+δ
M

,
··· ,e
− jθ
τ
M
1
−1
M
,··· ,e
− jθ

τ
M
1
−1
+δ
M

o
(5)
δ =
M
2
−1
∑
p=1
δ
p
(6)
W
M×M
=
h
W
τ
0
M
,W
τ
0
+δ
1
M
,W
τ
0
+δ
1
+δ
2
M
,· ·,W
τ
0
+δ
M
,··· ,
··· ,W
τ
M
1
−1
M
,··· ,W
τ
M
1
−1
+δ
M
i
T
(7)
W
τ
p
M
=

W
−

M−1
2

τ
p
M
,··· ,W

M−1
2

τ
p
M

T
(8)
X
M×1
(e
j
θ
M
) =
h
X

e
j
θ
M
·W
(M−1)
2
M

,··· ,
··· , X

e
j
θ
M
·W
−(M−1)
2
M

i
T
(9)
Y
M×1
(e
jθ
) =
h
Y
0
(e
jθ
),··· ,Y
M−1
(e
jθ
)
i
T
(10)
=
h
Y
s,0
(e
jθ
· e
j(M−1)π
),··· ,
···Y
s,M−1
(e
jθ
· e
j(M−1)π
)
i
T
. (11)
In the above definitions, W
M
= e
− j
2π
M
repre-
sents the twiddle factor. In Eq. (3), the vector
Y
s
M× 1
(e
jθ
) represents unmodulated bunched nonuni-
form samples in the frequency domain. The matri-
ces ∆
M× M
and W
M× M
are full rank matrices. The
vector X(e
j
θ
M
) in Eq. (3) consists of M number of
uniformly distributed, downsampled frequency bands
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
352

N
e
j
(M−1)
M
πn
X(e
jθ
)
∆
s,0
(e
jθ
)
↓ M
1
↓ M
2
N
e
− j(M−1)πn
Y
0
(e
jθ
)
Y
s,0
∆
1
s,0
(e
jθ
)
↓ M
2
N
e
− j(M−1)πn
Y
1
(e
jθ
)
∆
2
s,0
(e
jθ
)
∆
M
2
−1
s,0
(e
jθ
)
↓ M
2
↓ M
2
N
e
− j(M−1)πn
Y
2
(e
jθ
)
N
e
− j(M−1)πn
Y
M
2
−1
(e
jθ
)
N
e
j
(M−1)
M
πn
∆
s,M
1
−1
(e
jθ
)
↓ M
1
↓ M
2
N
e
− j(M−1)πn
Y
M
2
(M
1
−1)
(e
jθ
)
∆
1
s,M
1
−1
(e
jθ
)
↓ M
2
N
e
− j(M−1)πn
Y
M
2
(M
1
−1)+1
(e
jθ
)
∆
2
s,M
1
−1
(e
jθ
)
N
e
− j(M−1)πn
Y
M
2
(M
1
−1)+2
(e
jθ
)
↓ M
2
↓ M
2
∆
M
2
−1
s,M
1
−1
(e
jθ
)
N
e
− j(M−1)πn
Y
M−1
(e
jθ
)
Y
s,M−1
Figure 3: Alternative discrete time model of bunched nonuniform sampling scheme.
of the input signal X (e
jθ
) when applied to the anal-
ysis part of the uniform discrete Fourier transform
(DFT) modulated filter bank (Sommen and Janse,
2008; Vaidyanathan, 1993). The representation of
X(e
jθ
) in terms of X
(e
j
θ
M
) enhances the efficiency
of processing by optimizing the number of compu-
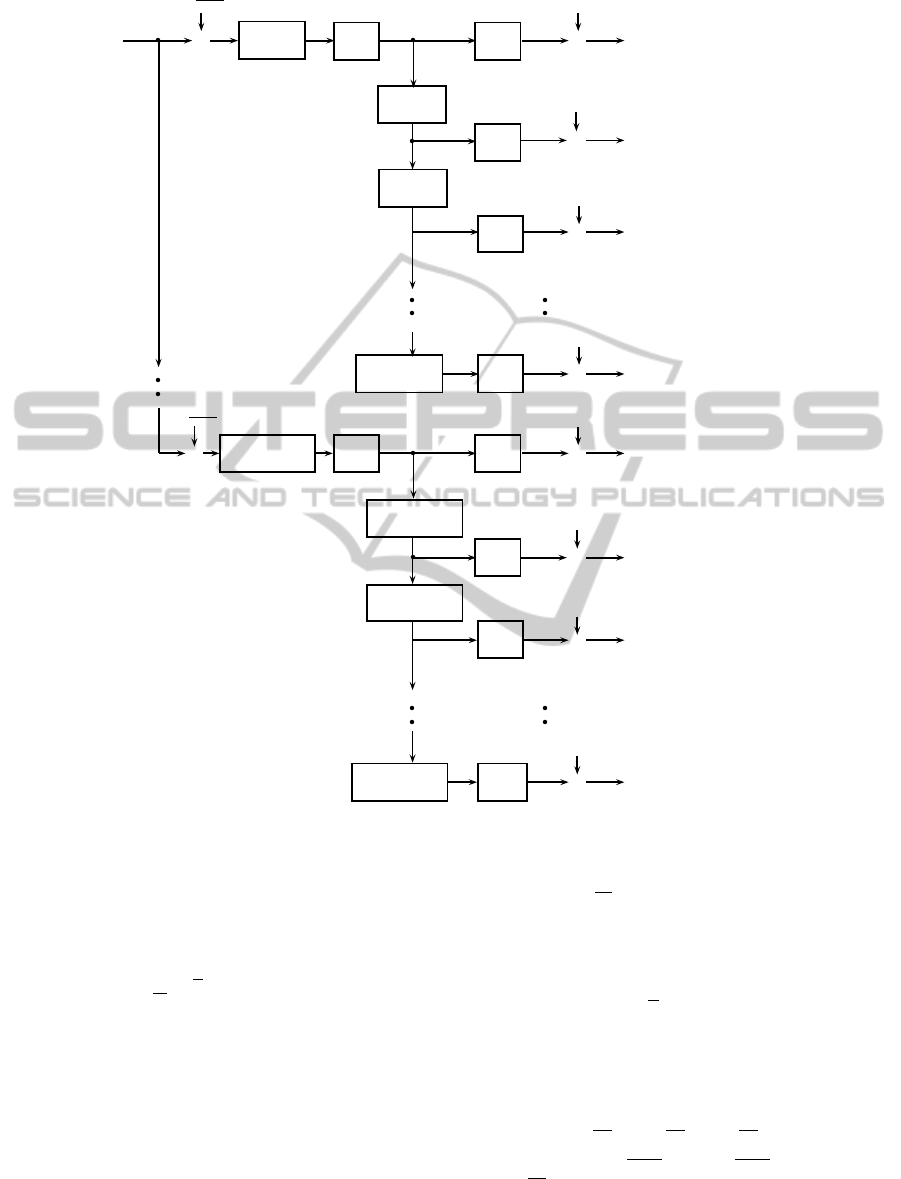
tations. Using Eqn. (3), we draw a structure to
relate uniform and bunched nonuniform samples as
shown in Fig. 4. This structure can be considered
as an extended version of the analysis part of uni-
form DFT modulated filter bank presented in (Som-
men and Janse, 2008). In Fig. 4, filters with fre-
quency responses H
p
M
(e
jθ
), p = 0, 1,· ·· ,M − 1, are
the polyphase components of the prototype filter used
in the uniform DFT filter bank (Sommen and Janse,
2008). The prototype filter is a lowpass filter with
cutoff frequency
π
M
. We note that these polyphase fil-
ters are allpass filters, with the frequency responses
as that of fractional delay filters (Sommen and Janse,
2008), i.e., for p = 0,1, ··· ,M − 1,
H
p
M
(e
jθ
) = e
j
θ
M
p
, −π ≤ θ < π. (12)
The block F
−1
s
in Fig. 4 represents a shifted M -
point inverse DFT matrix (Sommen and Janse, 2008),
which is defined as
F
s
=

W
0
M
,··· ,W
p
M
,··· ,W
M− 1
M

T
(13)
W
p
M
=

W
−
(M−1)
2
p
M
,··· ,W
(M−1)
2
p
M

T
. (14)
The reconstruction of uniform samples is simple and
perfect by inverting linear Eqn. (3). From Eqn. (3),
EFFICIENT RECONSTRUCTION OF UNIFORM SAMPLES FROM BUNCHED NONUNIFORM SAMPLES
353

x[n]
X(e
jθ
)
↓ M
H
0
M
(e
jθ
)
N
e
j(M−1)πn
↓ M
H
1
M
(e
jθ
)
N
e
j(M−1)πn
↓ M
H
M−1
M
(e
jθ
)
N
e
j(M−1)πn
e
− jθ
e
− jθ
F
−1
s
W
e
− j
θ
M
τ
0
e
− j
θ
M
(τ
0
+δ
1
)
e
− j
θ
M
(τ
M
1
−1
+δ)
Y
0
(e
jθ
)
Y
1
(e
jθ
)
Y
M−1
(e
jθ
)
N
e
− j(M−1)πn
N
e
− j(M−1)πn
N
e
− j(M−1)πn
Figure 4: Generation of bunched nonuniform samples.
Y
0
(e
jθ
)
e
j
θ
M
τ
0
N
e
j(M−1)πn
Y
1
(e
jθ
)
e
j
θ
M
(τ
0
+δ
1
)
N
e
j(M−1)πn
Y
M−1
(e
jθ
)
e
j
θ
M
(τ
M
1
−1
+δ)
N
e
j(M−1)πn
W
−1
F
s
↑ M
↑ M
↑ M
e
jθ
L
e
jθ
L
X(e
jθ
)
x[nT
0
]
e
− j
θ
M
.0
e
− j
θ
M
.1
e
− j
θ
M
.(M−1)
N
N
N
e
− j(M−1)πn
e
− j(M−1)πn
e
− j(M−1)πn
Figure 5: Reconstruction of uniform samples from bunched nonuniform samples.
we obtain
1
M
X
M× 1
(e
j
θ
M
) = W
−1
M× M
·∆
−1
M× M
·Y
s
M× 1
(e
jθ
). (15)
We use the synthesis part of the uniform DFT
modulated filter bank in order to obtain X(e
jθ
)
from X(e
j
θ
M
). The reconstruction of uniform samples
x[nT
0
] from bunched nonuniform samples is depicted
in Fig. 5, which is an extended version of the syn-
thesis part of the uniform DFT modulated filter bank
presented in (Sommen and Janse, 2008).
4 SIMULATION RESULTS AND
DISCUSSIONS
We have carried out simulation studies to verify
the performance of the proposed structures shown
in Figs. 4 and 5. Table 1 provides the set
of parameters considered for simulations.We have
considered 6,144 samples of two different sig-
nals x
1
[n] = sin[0.1πn] + 2sin[0.6πn] and x
2
[n] =
10
3
sin[0.6πn]/(πn) + 10
2
sin(0.7πn)/(πn) as inputs
for the simulations. Causal versions of the structures
presented in Figs. 4 and 5 are implemented with frac-
tional delay filters (Laakso et al., 1996) of order 184.
We have calculated the signal-to-error ratio (SER) as
defined in (Prendergast et al., 2004) and the absolute
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
354

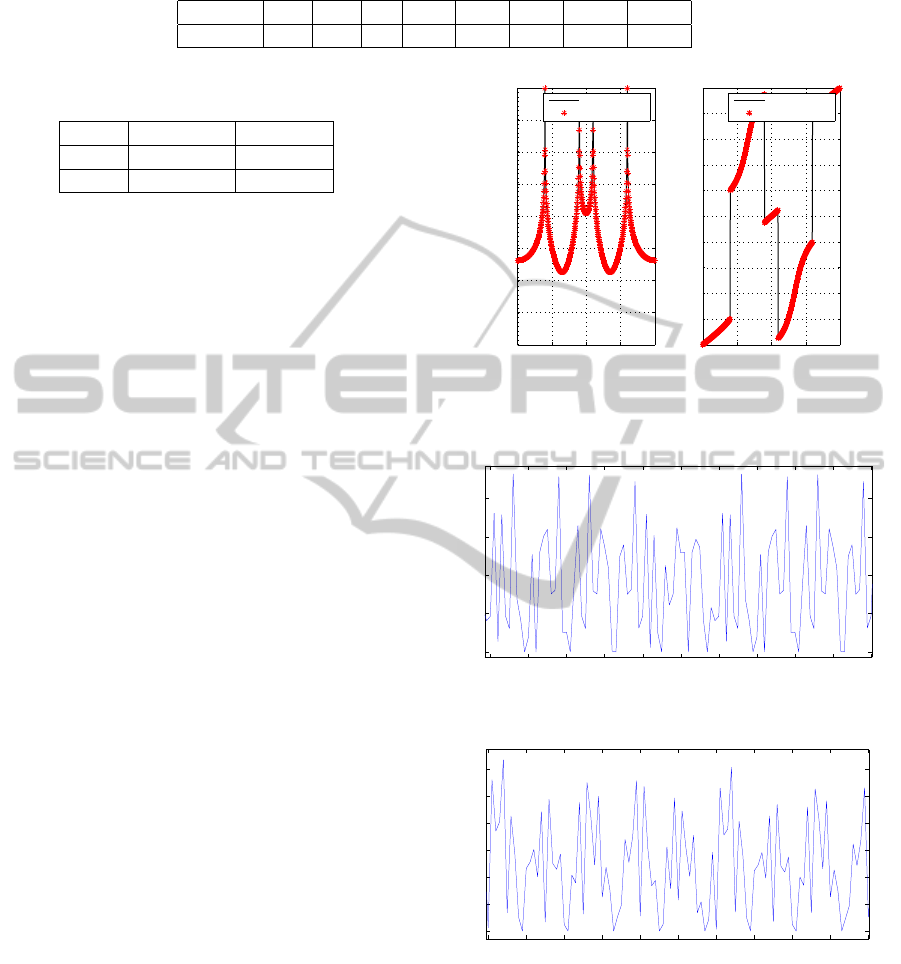
Table 1: Parameters considered for simulation.
T
0
[sec] M
1
M
2
τ
0
τ
1
τ
2
τ
3
δ
1
δ
2
1 4 3 0 2/3 4/3 6/3 11/3 12/3
Table 2: Performances of proposed structures.
Input AME [dB] SER [dB]
x
1
[n] −161 163
x
2
[n] −179 154
mean error (AME) defined in (Sommen and Janse,
2008) by considering 512 number of samples of both
the inputs and the respective reconstructed uniform
samples ex[n]. We compare x[n] and ex[n] by calculat-
ing the absolute error function e[n] for 512 samples,
where
e[n] = |x[n] − ex[n]|. (16)
The SER and AME for both the test signals are shown
in Table. 2 and these are calculated by considering all
possible shifts caused by the implementation of causal
fractional delay filters. Figure 6 shows the magnitude
and phase spectra for 512 samples of x
1
[n] and its
reconstructed uniform samples. It can be seen from
Fig. 6 that the results reflect the theory proposed for
the perfect reconstruction of uniform samples from
bunched nonuniform samples. Figures 7 and 8 de-
pict zoomed versions of e[n] for both the test signals
x
1
[n], x
2
[n] , respectively. It is evident from Figs.
7 and 8 that the reconstruction errors are very small
for both the input signals which are of the order of
10
−8
, 10
−9
, respectively. Even though it is proved
that perfect reconstruction is possible theoretically,
simulations show small reconstruction errors which
are due to finite length implementation of causal frac-
tional delay filters.
5 CONCLUSIONS
We have discussed the problem of reconstruction of
uniform samples from bunched nonuniform samples
using the synthesis part of a uniform discrete Fourier
transform (DFT) modulated filter bank. We con-
sidered a general case of unequal spacing between
bunches of nonuniform samples. The scheme pro-
posed for the reconstruction of uniform samples from
bunched nonuniform samples and the simulation re-
sults obtained show the efficiency of the signal pro-
cessing approach followed for the reconstruction of
uniform samples from bunched nonuniform samples.
−1 −0.5 0 0.5 1
−80
−70
−60
−50
−40
−30
−20
−10
0
Normalised frequency, θ
Magnitude [dB]
Input
Reconstructed
−1 −0.5 0 0.5 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
Normalised frequency, θ
Phase Φ ∈ [−π, π)
Input
Reconstructed
Figure 6: Magnitude and phase spectra of x
1
[n] and its re-
constructed uniform samples.
100 110 120 130 140 150 160 170 180 190 200
0
0.5
1
1.5
2
x 10
−8
Time index, n
Absolute error amplitude
Figure 7: Absolute error function of x
1
[n].
100 110 120 130 140 150 160 170 180 190 200
0
0.5
1
1.5
2
2.5
3
x 10
−9
Time index, n
Absolute error amplitude
Figure 8: Absolute error function of x
2
[n].
ACKNOWLEDGEMENTS
The authors wish to thank the three anonymous re-
viewers for their constructive criticisms and sugges-
tions which have greatly enhanced the presentation
and quality of the paper.
EFFICIENT RECONSTRUCTION OF UNIFORM SAMPLES FROM BUNCHED NONUNIFORM SAMPLES
355

REFERENCES
Black, W. and Hodges, D. (1980). Time interleaved con-
verter arrays. Solid-State Circuits, IEEE Journal of,
15(6):1022 – 1029.
Jerri, A. J. (1977). The shannon sampling theorem—its
various extensions and applications: a tutorial review.
Proceedings of the IEEE, 65(11):1565 – 1596.
Johansson, H. and L¨owenborg, P. (2006). Reconstruction of
nonuniformly sampled bandlimited signals by means
of time-varying discrete-time fir filters. EURASIP J.
Appl. Signal Process., pages 105–105.
Laakso, T., Valimaki, V., Karjalainen, M., and Laine, U.
(1996). Splitting the unit delay fir/all pass filters de-
sign. IEEE Signal Processing Magazine, 13(1):30 –
60.
Marvasti, F. A. (2001). Nonuniform sampling: Theory and
Practice. Plenum Pub Corp.
Oppenheim, A., Schafer, R., and Buck, J. (1999). Discrete-
time signal processing. Prentice-Hall, Inc., Engle-
wood Cliffs, NJ, USA, 2nd edition.
Ouderaa, E. V. D. and Renneboog, J. (1988). Some for-
mulas and applications of nonuniform sampling of
bandwidth-limited signals. IEEE Transactions on In-
strumentation and Measurement, IM-37:353–357.
Papoulis, A. (1977). Generalized sampling expansion.
IEEE Transactions on Circuits and Systems, CAS-
24:652–654.
Prendergast, R., Levy, B., and Hurst, P. (2004). Reconstruc-
tion of bandlimited periodic nonuniformly sampled
signals through multirate filter banks. IEEE Trans-
actions on Circuits and Systems I: Regular Papers,
51(8):1612 – 1622.
Singh, V. and Rajpal, N. (2007). Datacompression using
non - uniform sampling. In International Conference
on Signal Processing, Communications and Network-
ing, pages 603 –607.
Sommen, P. and Janse, K. (2008). On the relationship
between uniform and recurrent nonuniform discrete-
time sampling schemes. IEEE Transactions on Signal
Processing, 56(10-2):5147–5156.
Vaidyanathan, P. P. (1993). Multirate systems and filter
banks. Prentice-Hall, Inc., Upper Saddle River, NJ,
USA.
Wang, A., Wang, S., and Chen, M. (2004). A novel nonuni-
form sampling method and processing system to over-
come the nyquist rate limit and suppress the noise.
Proc. of the World congress on Intelligent Control and
Automation, pages 3842–3845.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
356