2-DOF PI-FUZZY CONTROLLERS FOR A MAGNETIC
LEVITATION SYSTEM
Claudia-Adina Dragoş, Radu-Emil Precup
Dept. of Automation and Appl. Inf., “Politehnica” University of Timisoara, Bd. V. Parvan 2, 300223 Timisoara, Romania
Emil M. Petriu
School of Information Technology and Eng., University of Ottawa, 800 King Edward, Ottawa, ON, K1N 6N5, Canada
Marius L. Tomescu
Computer Sci. Faculty, “Aurel Vlaicu” University of Arad, Complex Univ. M, Str. Elena Dragoi 2, 310330 Arad, Romania
Stefan Preitl, Radu-Codruţ David, Mircea-Bogdan Rădac
Dept. of Automation and Appl. Inf., “Politehnica” University of Timisoara, Bd. V. Parvan 2, 300223 Timisoara, Romania
Keywords: 2-DOF PI-fuzzy controllers, Cascade control system structures, Magnetic levitation system, PI controllers.
Abstract: This paper treats aspects concerning the design of two-degree-of-freedom (2-DOF) PI-fuzzy controllers
dedicated to the position control of magnetic levitation system. 2-DOF Mamdani and Takagi-Sugeno PI-
fuzzy controller structures based on the fuzzification of some linear blocks in the 2-DOF linear controller
structures are discussed. A design approach of three new cascade control system structures is offered. The
design approach carries out first the pole placement design of the inner state feedback control system. The
2-DOF PI-fuzzy controllers in the outer loops are next designed to merge separately designed linear PI
controllers accounting for the linearization of the process model at certain operating points. Samples of real-
time experimental results related to a laboratory equipment are given to validate the new fuzzy control
system structures and the design approach.
1 INTRODUCTION
The two-degree-of-freedom (2-DOF) controllers are
successful with respect to the one-degree-of-freedom
ones as they ensure very good control system
performance indices (overshoot, settling time, etc.)
defined in the performance specifications related to
reference input tracking and disturbance input
regulation (Åström, 1995; Araki, 2003; Bascetta,
2008; Precup et al., 2009). But the main drawback of
the control systems (CS) with 2-DOF controllers is
that the overshoot reduction is paid by slower
responses for reference input variations.
The systematic design and stability of fuzzy CS
have received much attention recently and many
significant results have been reported recently
(Gusikhin et al., 2007; Lam, 2009; Chohra et al.,
2010; Linda and Manic, 2011; Liu et al., 2011). The
fuzzy logic is inserted in 2-DOF CS structures to
ensure the further performance improvement. A 2-
DOF controller which involves a one-step-ahead
fuzzy prefilter in the feed-forward loop and a PI-
fuzzy controller in the feedback loop meant for the
foot trajectory tracking control of a hydraulically
actuated hexapod robot is discussed in (Barai and
Nonami, 2007). A 2-DOF CS that consists of a
conventional foreword internal model controller and
a feedback fuzzy controller for an electro-hydraulic
servo system is suggested in (Li and Xiong, 2008).
A simulated 2-DOF Mamdani fuzzy controller for
automotive semi-active suspension control is
presented in (Bei, 2009). Different structures of 2-
DOF Mamdani and Takagi-Sugeno (TS) PI(D)-
111
Drago¸s C., Precup R., Petriu E., L. Tomescu M., Preitl S., David R. and R
ˇ
adac M..
2-DOF PI-FUZZY CONTROLLERS FOR A MAGNETIC LEVITATION SYSTEM.
DOI: 10.5220/0003537201110116
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 111-116
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

fuzzy controllers applied to speed and position
control of servo systems are given in (Preitl et al.,
2010). Several nonlinear control approaches
including fuzzy control have been proposed recently
to deal with magnetic levitation systems. They
include the Lyapunov-based guaranteed stability
(Shameli et al., 2007), adaptive robust nonlinear
control (Wu and Hu, 2009) and fuzzy control
(Dragoş et al., 2010).
This paper suggests twofold contributions. First,
2-DOF PI-fuzzy controllers applicable as both
Mamdani and TS PI-fuzzy controller structures are
offered. Second, three cascade CS structures for a
magnetic levitation system laboratory equipment
(MLSLE) are proposed. The new CS structures
employ an inner state feedback CS and 2-DOF PI-
fuzzy controllers in the outer loops. The design
approach for these structures starts with the pole
placement design of the inner state feedback CS.
The 2-DOF PI-fuzzy controllers in the outer loops
are next designed to merge separately designed
linear PI controllers accounting for the linearization
of the process model at certain operating points.
Our new contributions are important and
advantageous with respect to other recent solutions
analyzed in the literature because they ensure very
good CS performance with respect to reference and
disturbance inputs. In addition, our fuzzy control
solutions belong to the class of low cost solutions as
the design approaches are relatively simple and the
structures are easily to implement.
This paper is organized as follows. The 2-DOF
PI-fuzzy controller structures are presented in
Section 2. The process models related to the MLSLE
are discussed in Section 3. The design of the new
CSs and samples of real-time experimental results
are given in Section 4. The concluding remarks are
highlighted in Section 5.
2 2-DOF PI-Fuzzy CONTROLLER
STRUCTURES
Three frequently used 2-DOF linear CS structures
focused on the linear PI(D) controller with the
transfer function (t.f.) C(s) are presented in Figure 1
as the set-point filter structure (a), the feedforward
structure (b) and the feedback structure (c) (Araki
and Taguchi, 2003; Precup et al., 2009). The main
variables in Figure 1 are r – the reference input, r
1
–
the filtered set-point, y – the controlled output, e=r–y
or e=r
1
–y – the control error, u – the control signal,
and d
1
, d
2
and d
3
– the three types of disturbance
inputs.
Figure 1: 2-DOF linear CS structures.
In Figure 1, P(s) indicates the t.f. of the plant
which is linear in this case but generally nonlinear in
2-DOF PI(D)-fuzzy CS structures. The t.f C(s) of PI
controller is
ssTksC
cc
/)1()(
+
=
,
(1)
where k
c
is the controller gain and T
c
is the integral
time constant.
The expressions of the t.f. of the reference input
filter, referred to also as set-point filter, in Figure 1
(a) and of the t.f. of the rest of two blocks in Figure
1 (b) and (c) are
./)1()(
),()(
0 ),1/()1()(
*
ssTksC
TTksC
TsTsTsF
Fc
FccF
FcF
+=
−=
≥
+
+
=
,
(2)
where
F
T
is the filter time constant.
The 2-DOF CS structures presented in Figure 1
(a), (b) and (c) are equivalent as they are
characterized by the same controller t.f. in the linear
case:
./)1()(/)()(
,/)1()(/)()(
,
,
ssTksrsusG
ssTksysusG
Fcru
ccyu
+==
+−
=
=
(3)
They will be fuzzified as follows aiming the CS
performance enhancement.
An alternative to the operational representation
of the t.f.s of the three 2-DOF controllers is based on
in the definition of the generic PI block with the t.f.
0 ,/) 1()( ≥ττ+=
τ
ssksG
c
.
(4)
The t.f. defined in (4) is used in different
particular forms to express the components with
dynamics in Figure 1 to be fuzzified. The
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
112

fuzzification of the block with the t.f. C(s) in the set-
point filter structure and in the feedforward structure
is based on the following relationship that results
from (1) and (4):
)()( sGsC
c
T
=
.
(5)
The fuzzification of the block with the t.f. C
*
(s)
is supported by (2) and (5) that lead to
)()(
*
sGsC
F
T
=
.
(6)
The fuzzification of the generic PI block with the
t.f. defined in (4) starts with its discretization. The
fuzzification results in the fuzzy block FB-τ
presented in Figure 2 (a), where FB is the Mamdani
or the TS fuzzy block without dynamics (Preitl et al.,
2010). The block FB is based on the input
membership functions with the shapes and
parameters defined in Figure 2 (b). These input
membership functions are used in the Mamdani
fuzzy block and in the TS fuzzy block as well; the
output membership functions are defined only for
the Mamdani fuzzy block. The low cost aim was
accounted for to set three input membership
functions for each FB input.
Figure 2: Structure (a) and membership functions (b) of
block FB-τ.
The tuning parameters of the block FB-τ (shown
in Figure 2 (b)) are
e
B
,
e
B
Δ
and
u
B
Δ
for the
Mamdani fuzzy block FB-τ, and
e
B
and
e
B
Δ
for the
TS fuzzy block FB-τ. The discretization involves
setting the sampling period T
s
in accordance with the
requirements of quasi-continuous digital control.
Tustin’s method is next applied to discretize the
continuous-time linear PI block with the t.f.
)(sG
τ
resulting in the recurrent equation of the incremental
digital generic PI block and on its parameters given
in (7) and (8), respectively:
)]( )([)( kekeKku
P
μ+Δ=Δ
,
(7)
)2/(2 ),2/(
ssscP
TTTkK −τ=
μ
−τ=
.
(8)
Mamdani’s MAX-MIN composition is used in
the inference engine of the Mamdani fuzzy block
FB-τ, and the centre of gravity method is used in the
defuzzification module of FB-τ. The SUM and
PROD operators are used in the inference engine of
the TS fuzzy block FB-τ, and the weighted average
method is used in the defuzzification module of FB-
τ. The rule base of the TS fuzzy block FB-τ is (Preitl
et al., 2010):
. )]()([)( THEN
N IS )( AND P IS )( IF :9 Rule
)],()([)( THEN
P IS )( AND N IS )( IF :1 Rule
99
11
kekeKku
keke
kekeKku
keke
P
P
μ+Δ=Δ
Δ
μ+Δ=Δ
Δ
#
(9)
The superscripts presented in (9) indicate the
index of the certain rule. For complete rule bases as
those presented in (9) the superscripts highlight the
possibility to carry out the separate design of a
maximum of nine linear PI controllers. The blocks
FB-τ will behave like bumpless interpolators
between these separately designed PI controllers as
shown in the next section.
The unified structures of 2-DOF PI-fuzzy
controllers are presented in Figure 3.
Figure 3: 2-DOF PI-fuzzy controller structures.
They are referred to as set-point filter 2-DOF PI-
fuzzy controller (a), the feedforward 2-DOF PI-
fuzzy controller (b) and the feedback 2-DOF PI-
fuzzy controller (c). The linear blocks can be
discretized to ensure the discrete-time treatment of
all signals in the 2-DOF PI-fuzzy controller
structures to increase the application areas.
3 MODELS OF MAGNETIC
LEVITATION SYSTEM
The nonlinear state-space model of the MLSLE is
2-DOF PI-FUZZY CONTROLLERS FOR A MAGNETIC LEVITATION SYSTEM
113

,
),(/)(
),(/)(
,/),(/),(
,
1
1424
1313
4123112
21
xy
xxfxcukx
xfxcukx
mxxFgmxxFx
xx
diii
iii
EMEM
=
−−+=
−+=
++−=
=




(10)
where x
1
is the sphere position 0≤ x
1
≤0.016 m, x
2
is
the sphere speed, x
3
and x
4
, are the currents in the
upper and lower electromagnetic coil, respectively
0.038 A≤x
3
,x
4
≤2.38 A, u
1
and u
2
are the voltages
applied to the upper and lower electromagnet,
respectively 0.0049≤u
1
,u
2
≤1, g is the gravity
acceleration, m is the sphere mass, y is the controlled
output, x
d
is the distance between electromagnets
minus the sphere diameter, and the parameters k
i
and
c
i
set the actuator dynamics. The control signal is
applied to the upper electromagnet (EM1), u=u
1
, and
the disturbance input is applied to the lower
electromagnet (EM2) d=u
2
. The numerical values of
the parameters are given in (Inteco, 2008).
We are carrying out the linearization of the
nonlinear model (10) at several operating points
A
j
(x
10
, x
2o
, x
3
, x
40
) (with j – the index of the operating
point) to meet the control objectives and also to offer
low cost solutions. Accepting u
2
=0 (the state
variable x
4
is neglected but its effect is not) the
following general linearized state-space
mathematical model is employed in the design:
,
,
xc
bxAx
Δ=Δ
Δ
+
Δ=Δ
T
y
u

(11)
where ∆u=u–u
0
and ∆y=y–y
0
are the differences of
the variables u and y with respect to their values at
the operating point, u
0
and y
0
, respectively, ∆x=[∆x
1
∆x
2
∆x
3
∆x
4
]
T
is the state vector, and the superscript
T indicates the matrix transposition. For three
operating points A
1
(0.007,0,0.3,0), A
2
(0.008,0,0.285,
0), A
3
(0.009,0,0.6,0) the expressions of the matrices
in (11) are
].001[)(
,
786.8
0
0
,
3186020224
9339308.132
010
],001[)(
,
468.8
0
0
,
3186018125
6031708.186
010
],001[)(
,
376.6
0
0
,
6149015056
5028908244
010
3
33
2
22
1
11
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
T
T
T
.
.
.
.
.
..
c
bA
c
bA
c
bA
(12)
4 CONTROLLER DESIGN AND
EXPERIMENTAL RESULTS
The cascade CS structures are represented by the
unified structure presented in Figure 4, where r
x
is
the reference input for the inner state feedback
control loop,
T
k
is the state feedback gain matrix,
and the MLSLE process includes the actuators and
sensors dynamics.
The unified design approach dedicated to 2-DOF
PI-fuzzy controllers consists of six design steps.
 Step I. Apply the pole placement method to the
linearized state-space models (11) and obtain the
state feedback gain matrix
]0075.0536[k
T
=
Figure 4: Unified cascade CS structure.
 Step II. Express the t.f.s of the inner state
feedback control loops resulted from (12):
}.3,2,1{
,
])(21)[1(
)(
22
1
∈
+ξ++
=
ΣΣ
j
sTsTsT
k
sP
jjjj
P
j
(13)
 Step III. Apply a linear design method to tune
the parameters of the 2-DOF linear PI
controllers for the processes with the t.f.s (13).
 Step IV. Set the sampling period T
s
, according
to the requirements of quasi-continuous digital
control, (T
s
=0.01s in our case), take into account
the zero-order hold, and discretize the
continuous-time 2-DOF PI linear controllers
resulting in the parameters
BMSB
P
M
P
S
P
KKK μ<μ<μ<< ,
.
(14)
 Step V. Set the parameter Be=0.05 and apply
the tuning conditions
e
BS
Pue
B
e
BKBBB , μ=μ=
ΔΔ
,
(15)
 Step VI. Formulate the rule base (13) of the TS
fuzzy block FB-τ:
. ,
,
, ,
,
738
462951
7384
62951
BM
S
B
PPP
M
PPP
PP
S
PPPP
KKKKKK
KKKKKK
μ<μ=μμ=μ=
μ=μ=μμμ=μ=μ
=====
====
(16)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
114

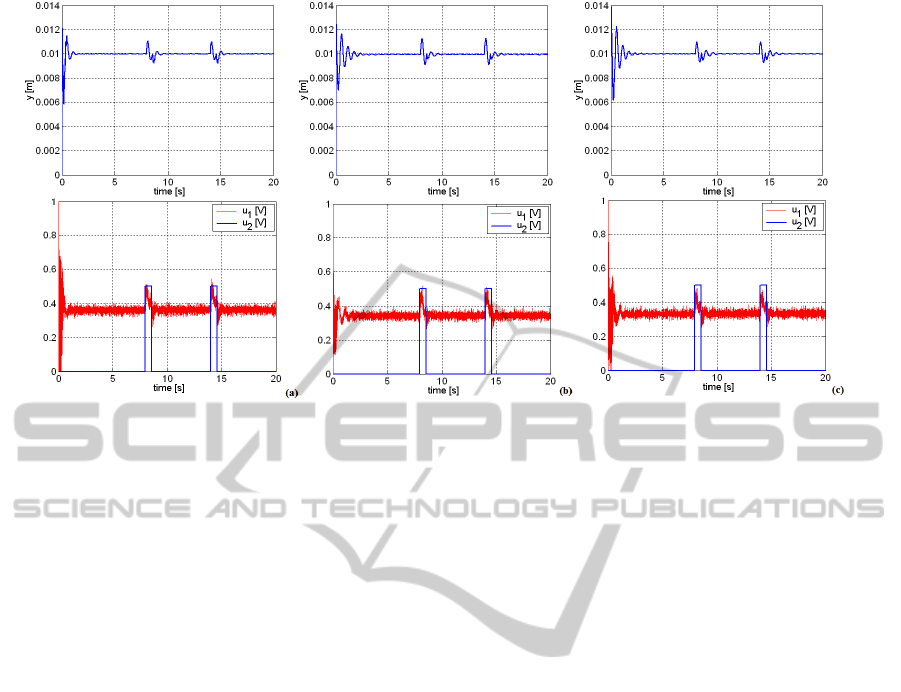
Figure 5: Experimental results for the TS fuzzy CS with the set-point filter (a), with the feedforward (b) and with the
feedback (c) 2-DOF PI-fuzzy controller: position (y), control signal
1
uu
=
and disturbance input
2
ud =
versus time.
The tuning conditions (15) are obtained from the
modal equivalence principle in order to guarantee
the quasi-PI behaviour of the Mamdani fuzzy block
FB-τ and of the TS fuzzy block FB-τ. Both tuning
conditions are applied in the tuning of Mamdani
fuzzy block FB-τ, and the first one is applied in the
tuning of TS fuzzy block FB-τ. The setting of the
parameter B
e
is important. The experience of CS
designer can be taken into consideration but other
mathematical or engineering analyses can be taken
into consideration including the stability analysis
(Škrjanc et al., 2005). The linear blocks in Figure 3
are implemented for one of the linear controllers that
correspond to (14), and the results are presented as
follows for
S
P
K
and
S
μ
.
Some real-time experimental results for the TS
fuzzy CSs with the set-point filter 2-DOF PI-fuzzy
controller, with the feedforward 2-DOF PI-fuzzy
controller, and the feedback 2-DOF PI-fuzzy
controller, are presented in Figures 5. The
experimental scenario is characterized by the
application of a step reference input
m 01.0=r
and
of a pulse width modulated disturbance input.
The results presented in Figure 5 show very good
CS performance indices, therefore our new fuzzy
controllers are validated. The best performance
indices (in terms of overshoot and settling time) are
exhibited by the fuzzy CS with the set-point filter 2-
DOF PI-fuzzy controller.
5 CONCLUSIONS
This paper has suggested a new generation of 2-
DOF PI-fuzzy controller structures that consists of
three fuzzy CS structures. A unified approach to the
design of these fuzzy controller structures that
enables the design of both Mamdani and TS fuzzy
controllers has bee offered with focus on the
position control of an MLSLE.
Our approach is justified because of the process
nonlinearities. Therefore very good CS performance
is ensured by means of low cost fuzzy controllers.
Future research will be focused on the
convenient proof of the stability of the 2-DOF fuzzy
control structures. Extensions to other models and
processes are targeted.
ACKNOWLEDGEMENTS
This work was partially supported by the UEFISCDI
of Romania, and by the strategic grant POSDRU
6/1.5/S/13 (2008) of the Ministry of Labour, Family
and Social Protection, Romania, co-financed by the
European Social Fund – Investing in People.
REFERENCES
Araki, M., Taguchi, H., 2003. Two-degree-of-freedom
PID controllers, International Journal of Control,
Automation, and Systems. 1, 401-411.
2-DOF PI-FUZZY CONTROLLERS FOR A MAGNETIC LEVITATION SYSTEM
115

Åström, K.-J., Hägglund, T., 1995. PID Controllers
Theory: Design and Tuning. Research Triangle Park,
NC: Instrument Society of America.
Barai, R. K., Nonami, K., 2007. Optimal two-degree-of-
freedom fuzzy control for locomotion control of a
hydraulically actuated hexapod robot. Information
Sciences. 177, 1892-1915.
Bascetta, L., Leva, A., 2008. FIR based causal design of 2-
d.o.f. controllers for optimal set point tracking.
Journal of Process Control. 18, 465-478.
Bei, S.-Y., 2009. Fuzzy controller for automotive semi-
active suspension based on damping control. In
Proceedings of 2009 ISECS International Colloquium
on Computing, Communication, Control, and Mana-
gement (CCCM 2009). Sanya, China, 4, 296-299.
Chohra, A., Madani, K., Kanzari, D., 2010. Fuzzy
cognitive and social negotiation agent strategy for
computational collective intelligence. Transactions on
Computational Collective Intelligence. 1, 143-159.
Dragoş, C.-A., Preitl, S., Precup, R.-E., Bulzan, R.-G.,
Pozna, C., Tar, J. K., 2010b. Takagi-Sugeno fuzzy
controller for a magnetic levitation system laboratory
equipment. In Proceedings of International Joint
Conferences on Computational Cybernetics and Te-
chnical Informatics (ICCC-CONTI 2010). Timisoara,
Romania, 55-60.
Gusikhin, O., Rychtyckyj, N., Filev, D., 2007. Intelligent
systems in the automotive industry: applications and
trends. Knowledge and Information Systems. 12, 147-
168.
Inteco Ltd, 2008. Magnetic Levitation System 2EM
(MLS2EM), User’s Manual (Laboratory Set). Krakow,
Poland: Inteco Ltd.
Lam, H. K., 2009. Stability analysis of sampled-data fuzzy
controller for nonlinear systems based on switching T-
S fuzzy model. Nonlinear Analysis: Hybrid Systems.
3, 418-432.
Li, H., Xiong, S., 2008. A new type of control method for
electro-hydraulic servo systems. In Proceedings of 7
th
World Congress on Intelligent Control and Auto-
mation (WCICA 2008). Chongqing, China, 6450-6453.
Linda, O., Manic, M., 2011. Online spatio-temporal risk
assessment for intelligent transportation systems.
IEEE Transactions on Intelligent Transportation
Systems. 12, 194-200.
Liu, Y.-J., Tong, S.-C., Li, T.-S., 2011. Observer-based
adaptive fuzzy tracking control for a class of uncertain
nonlinear MIMO systems. Fuzzy Sets and Systems.
164, 25-44.
Precup, R.-E., Preitl, S., Petriu, E. M., Tar, J. K.,
Tomescu, M. L., Pozna, C., 2009. Generic two-degree-
of-freedom linear and fuzzy controllers for integral
processes. Journal of The Franklin Institute. 346, 980-
1003.
Preitl, S., Precup, R.-E., Dragoş, C.-A., Rădac, M.-B.,
2010. Tuning of 2-DOF fuzzy PI(D) controllers.
Laboratory applications. In Proceedings of 11
th
IEEE
International Symposium on Computational Intelli-
gence and Informatics (CINTI 2010), Budapest,
Hungary, 237-242.
Shameli, E., Khamesee, M. B., Huissoon, J. P., 2007.
Nonlinear controller design for a magnetic levitation
device. Microsystem Technologies. 13, pp. 831-835.
Škrjanc, I., Blažič, S., Agamennoni, O., 2005. Interval
fuzzy model identification using l
∞
-norm. IEEE Tran-
sactions on Fuzzy Systems. 13, 561-568.
Wu, H., Hu, Y., 2009. Study on fuzzy control algorithm
for magnetic levitated platform. In Proceedings of
2009 International Conference on Measuring Te-
chnology and Mechatronics Automation (ICMTMA
2009). Hunan, China, 2, 598-601.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
116