
CAUSAL REASONING IMPROVED BY FUZZY LOGIC
FOR DIAGNOSIS OF BOND GRAPH MODELLED
UNCERTAIN PARAMETERS SYSTEMS
Walid Bouallègue, Salma Bouslama Bouabdallah
LACS, National Engineering School of Tunis, BP 37, Le Belvedere, 1002, Tunis, Tunisia
Moncef Tagina
L3I, National School of Computer Sciences, Manouba, Tunisia
Keywords: Fault detection and isolation (FDI), Bond graph (BG), Parameters uncertainties, Fuzzy logic, Causal
reasoning.
Abstract: In this paper, a method for on-line fault detection and isolation (FDI) of bond graph (BG) modelled
uncertain parameters systems is proposed. In this case, we don’t have to calculate the Analytical
Redundancy Relations (RRAs) since residuals are directly generated from the Diagnostic Bond Graph
(DBG). Detection is based on fuzzy logic approach. For isolation, two methods exploiting the causal
properties of the BG model are used: Fault Signature Matrix (FSM), and exoneration. A real simulation
example is provided to show the efficiency of the proposed methods.
1 INTRODUCTION
Presently, Fault Detection and Isolation (FDI) is an
increasingly active research domain. FDI consists in
identifying when a fault has occurred, the type of
fault and its location. A widespread solution for FDI
consists in comparing the behaviour of the real
system to a theorical model.
FDI methods can be divided into three
categories: quantitative methods, qualitative
methods and process history based methods
(Staroswiecki, 2000); (Venkatasubramanian,
2003.a); (Venkatasubramanian, 2003.b); (Venkata-
subramanian, 2003.c).
The most frequently quantitative diagnosis
approaches are based on Analytical Redundancy
Relations (ARRs), Kalman filters and parameter
estimation. The ARRs are relations comparing
informations given by the real process to those
generated by the theorical model.
The qualitative methods are based on qualitative
models such as causal graphs, fault trees or
abstraction hierarchies … (Montmain and Gentil,
1999). These models are obtained by analyzing the
cause and effect relationships in the process and the
association of observations (symptoms) to failures
using qualitative operators.
Because of its behavioural, structural and causal
properties, the BG tool is used in complex processes
modelling and FDI (Samantaray and al., 2008);
(Dauphin-Tanguy, 2000); (Dauphin-Tanguy and
Tagina, 2000). Its causal properties are used to
determine the fault origins; Bond Graph is exploited
in both qualitative and quantitative diagnosis
methods (Samantaray et al., 2008).
Qualitative methods transform the BG model to a
qualitative model expressing the states of variables
with qualitative states ([+], [-] or 0) (Montmain and
Gentil, 1999). When an inconsistency (fault) is
detected, backward and forward propagation
procedure can be used for isolation. The BG model
can also be transformed to a Temporal Causal Graph
(TCG) or tree graph that can be used for FDI
(Samantaray et al., 2008).
In quantitative approaches, many methods are
proposed. By covering the causal paths in the BG
model, Analytical Redundancy Relations (ARRs)
can be derived from the energy conservation laws in
junctions 0 and 1, the principle of fault signature can
then be used to isolate the fault affecting sensors and
59
Bouallègue W., Bouslama Bouabdallah S. and Tagina M..
CAUSAL REASONING IMPROVED BY FUZZY LOGIC FOR DIAGNOSIS OF BOND GRAPH MODELLED UNCERTAIN PARAMETERS SYSTEMS.
DOI: 10.5220/0003537500590066
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 59-66
ISBN: 978-989-8425-75-1
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
actuators (Tagina, 1995). In (Samantaray et al.,
2006), residuals are directly generated in the
Diagnostic Bond Graph (DBG), and a fault signature
matrix (FSM) is elaborated by covering causal paths
from residuals detectors to the components.
Therefore, the efficiency and robustness of these
methods depend on the model’s accuracy.
In case of uncertain parameters systems, (Djeziri,
2007); (Djeziri et al., 2009) proposed a robust
diagnosis algorithm, from a BG model in Linear
Fractional Transformations (LFT) form. They
derived ARRs in which they separated the quantity
of energy given by the uncertain part from the
residual to be evaluated, this idea allows the
generation of adaptive thresholds for fault detection.
A study of sensitivity was elaborated to deduce
detectability indexes defining the detectable value of
the residual in case of faults and parameters
uncertainties. In (Bouallègue et al., 2010), a method
for robust fixed and adaptive thresholds is proposed.
This method exploits the sensitivity of residuals to
different system parameters in order to determine
their thresholds; the FSM is used for isolation. In
(Bouslama-Bouabdallah et al., 2006), a fuzzy logic
approach applied to residuals deduced from the BG
model is used in detection stage. For isolation, the
FSM is transformed into inference rules allowing the
determination of the fault’s origin.
The main contribution of this paper is to use the
bond graph model directly in the task of robust FDI
in case of uncertain parameters systems. The
detection module is based on a fuzzy logic system.
For isolation, two causal reasoning based methods
were proposed.
This paper is organized as follows: Section 2
details the notion of DBG used to generate directly
the residuals in the BG model. Section 3 describes
the proposed fuzzy detection method. Section 4
presents two isolation methods: signature matrix and
exoneration. Section 5 describes the hydraulic
benchmark composed of three tanks. Finally,
different results and their interpretations are given in
section 6.
2 RESIDUALS GENERATION
FROM DBG
The generation of Analytical Redundancy Relations
(ARRs) from the bond graph model uses the
structural relations given by the conservation law in
all 0 and 1 junctions and aims to express the
unknown variables by those known (inputs and
sensors). This method cannot deal with algebraic
loops, so, unknown variables cannot be eliminated.
So, the structural independence of the different
residuals has to be checked with existing residuals.
In (Samantaray et al., 2006), a direct method for
ARR generation from BG model is proposed. The
causality inversion of detectors (which are
considered as sources) has been proposed as a
unified approach to generate residuals.
When the bond graph model is assigned
preferred differential causality and using inversion
of sensor causalities, if necessary, the following five
compositions are possible (Samantaray et al., 2006):
1. Inverted causality in effort sensor (De),
2. Inverted causality in flow sensor (Df),
3. non-inverted causality in effort sensor (De),
4. non-inverted causality in flow sensor (Df),
5. Inversion of signal sensor, Ds, to signal
source, Ss (for controllers).
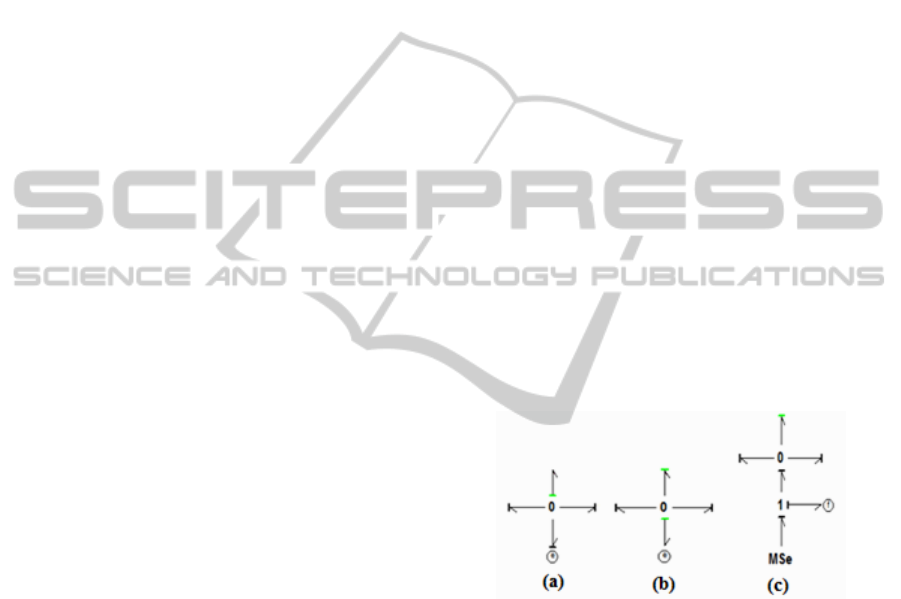
Let us consider the case of inverted causality in
the effort sensor, De, (see Figure 1). This sensor will
be equivalent to an effort source (measurements
from real process), so expression of the source
loading flow variable is equated to zero (Samantaray
et al., 2006). This expression is a residual (it does
not involve any states, since all storage elements are
in differential causality) which’s measured by a
virtual flow sensor (Samantaray et al., 2006).
Figure 1: (a) Sensor e in behavioral model, (b) inverted
causality in e and (c) substituted representation for
inverted causality in e.
The bond graph of the system with these
substitutions using preferred derivative causality is
called the Diagnostic Bond Graph (DBG)
(Samantaray et al., 2008).
3 DETECTION USING FUZZY
LOGIC APPROACH
In ideal conditions, residual value is equal to zero in
fault free context. In practice, due to the uncertainty
and the measurement noise, residuals are different
from zero. Thresholds are used to deduce whether
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
60

systems are in normal functioning mode or faulty
mode. Unfortunately, thresholds near to zero can
cause false alarms problems because of noise
variation; and assigning larger thresholds reduce the
fault detection sensitivity (Frank et al., 1997).
Fuzzy logic is the most common solution to
overcome the uncertainty problems. Many works
used this approach in residuals processing in order to
know the system state (Evsukoff et al., 2000)
(Bouslama-Bouabdallah et al., 2006).
In this work, we propose fuzzy processing of
residuals generated by the DBG in the task of fault
detection in case of parameters uncertainty.
From residuals values, two features can be
extracted:
• The absolute value of the residuals: r
• Residual variation over a sliding time
window: d
1
1
1
tN
it
dr(i)r(i)
N
+−
=
=−−
∑
The choice of the parameter N depends on the
residual variation and the noise effects, it is fixed
experimentally until we can get clearly the signal
trend.
The descriptor sets associated with each feature
fuzzy partition are:
r= {“SMALL”, “LARGE”}
d= {“SMALL”, “LARGE”}
These two variables are fuzzified using two
trapezoidal membership functions (Figure 2). So,
four parameters have to be determined for each
function.
Figure 2: Fuzzy sets of the residuals.
The trapezoidal boundaries of the set SMALL are
given by:
r : μ
small
=[0, 0, r-max, Rmin]
d : μ
small
=[0, 0, d-max, Dmin]
And for the set LARGE, they are given by:
r : μ
Large
=[r-max, Rmin, Rmax, Rmax]
d : μ
Large
=[d-max, Dmin, Dmax, Dmax]
Where:
r-max respectively d-max is the maximum value
of the residual respectively residual variation in
normal operating mode
Rmin = K
r
* r-max.
Dmin= K
d
*d-max ,
K
r
, K
d
is fixed experimentally.
Rmax respectively Dmax: is the maximum value
respectively variation of residual in faulty case.
For each residual, we have established a set of
inference rules which are presented in the following
table:
Table 1: Rules base of the fuzzy system.
r
d
Small Large
Small Normal Fault
Large Fault Fault
Rules are obtained using MIN-MAX inference
method, the MIN operator represents the logic
function AND, and the MAX operator for the logic
function OR.
The output of this fuzzy system is a fault index
indicating whether the concerned residual is in
normal operating mode or faulty mode (Figure 3).
Figure 3: Residual defuzzification.
4 THE PROPOSED FAULT
ISOLATION METHODS
Many procedures issued from FDI and Artificial
Intelligence communities were proposed in the task
of Fault Isolation. Causal properties of the BG tool
could be used in many methods such as Fault
Signature Matrix (FSM) and the exoneration
algorithm. In this work, these two methods are
combined with fuzzy reasoning in order to improve
FDI efficiency.
4.1 Signature Matrix
In FDI terminology, the Fault Signature Matrix
(FSM) crosses ARRs in rows and faults in column
(Cordier et al., 2004) (Biswas et al., 2009). Fault
isolation uses structural properties of the ARR
expressed in terms of a binary fault signature matrix
S, which describes the participation of various
CAUSAL REASONING IMPROVED BY FUZZY LOGIC FOR DIAGNOSIS OF BOND GRAPH MODELLED
UNCERTAIN PARAMETERS SYSTEMS
61

components (physical devices, sensors, actuators and
controllers) in each residual and forms a structure
that links the discrepancies in components to
changes in the residuals (Cordier et al., 2004).
Let us consider that fj is a fault affecting
component Cj, then in the binary fault signature
matrix F is,
0
1
, if the occurence of fault fj does not affect ARRi
, if the fault fj will violate ARRi
F
ij
=
⎧
⎨
⎩
From the DBG model, the analysis of the causal
paths to each residual is used to generate these
signatures (Samantaray et al., 2006). In fact, every
component causally linked to the residual detector
can affect its value. Let us consider the DBG of
Figure 4:
Figure 4: Example of DBG.
If we consider residual detector r1, the next causal
paths can be found:
CÆf4Æf2Æf1Ær1
RÆf5Æf2Æf1Ær1
PÆe6Æe2Æe4ÆCÆf4Æf2Æf1Ær1
Then, any variation in components C, R and
sensor P can affect the value of residual r1. In the
same way, and using all residuals, we can deduce the
FSM.
In this work, fuzzy detection module output is
exploited in isolation task. So, a fuzzy fault
signature matrix F is defined as follows:
Small , if the occurence of fault fj does not affect ARRi
L arg e, if the fault fj will violate ARRi
F
ij
=
⎧
⎨
⎩
4.2 Exoneration
4.2.1 Principle of Exoneration
Exoneration principle is a fundamental concept that
is often used implicitly in diagnosis (Cordier et al.,
2004); (Fagarasan et al., 2004). It uses consistency
of tests (residuals) to check if its support can be
faulty or not. The supports of a residual are variables
that can affect it and change its value. The
exoneration algorithm manages two lists, a list of
components whose state is normal, LN and a list of
suspect components LS. LS is made by the union of
the inconsistent test supports that are not exonerated
by the consistent tests (Fagarasan et al., 2004).
The steps of the algorithm are the followings
(Fagarasan et al., 2004):
1. Initialize L
N
and L
S
to the empty list
=
={Ø}.
2. At each sampling time and for each test Ti:
2.1. IF Ti result is consistent, THEN Ti support Ci
is considered normal thus added to L
N
, L
N
={C
i
ᴗL
N
}
and deleted from L
S
, L
S
=L
S
\C
i
2.2. IF Ti result is inconsistent, Ti support Ci is
suspected of being faulty and its components that
are not in L
N
are added to L
S
,L
S
={C
i
ᴗL
S
}\L
N
.
Finally, after the analysis of the tests, the
components in L
S
represent the final diagnosis.
4.2.2 Exoneration Improved by Fuzzy Logic
This algorithm is based on fuzzy logic to check the
consistency of the residuals. To use the fuzzy
detection module results, some improvements have
to be done.
1. Initialize L
N
and L
S
to the empty list
=
={Ø}
2. At each sampling time and for each test Ti:
2.1. IF Ti result is NORMAL, then Ti
support Ci is considered normal thus added to
L
N
, L
N
={C
i
ᴗL
N
} and deleted from L
S
, L
S
=L
S
\C
i
2.2. IF Ti result is FAULT, then Ti support
Ci is suspected of being faulty and its
components that are not in L
N
are added to
L
S
,L
S
={C
i
ᴗL
S
}\L
N
5 APPLICATION EXAMPLE
5.1 Test Bench Presentation
Let us consider the following hydraulic system
(Figure 5):
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
62
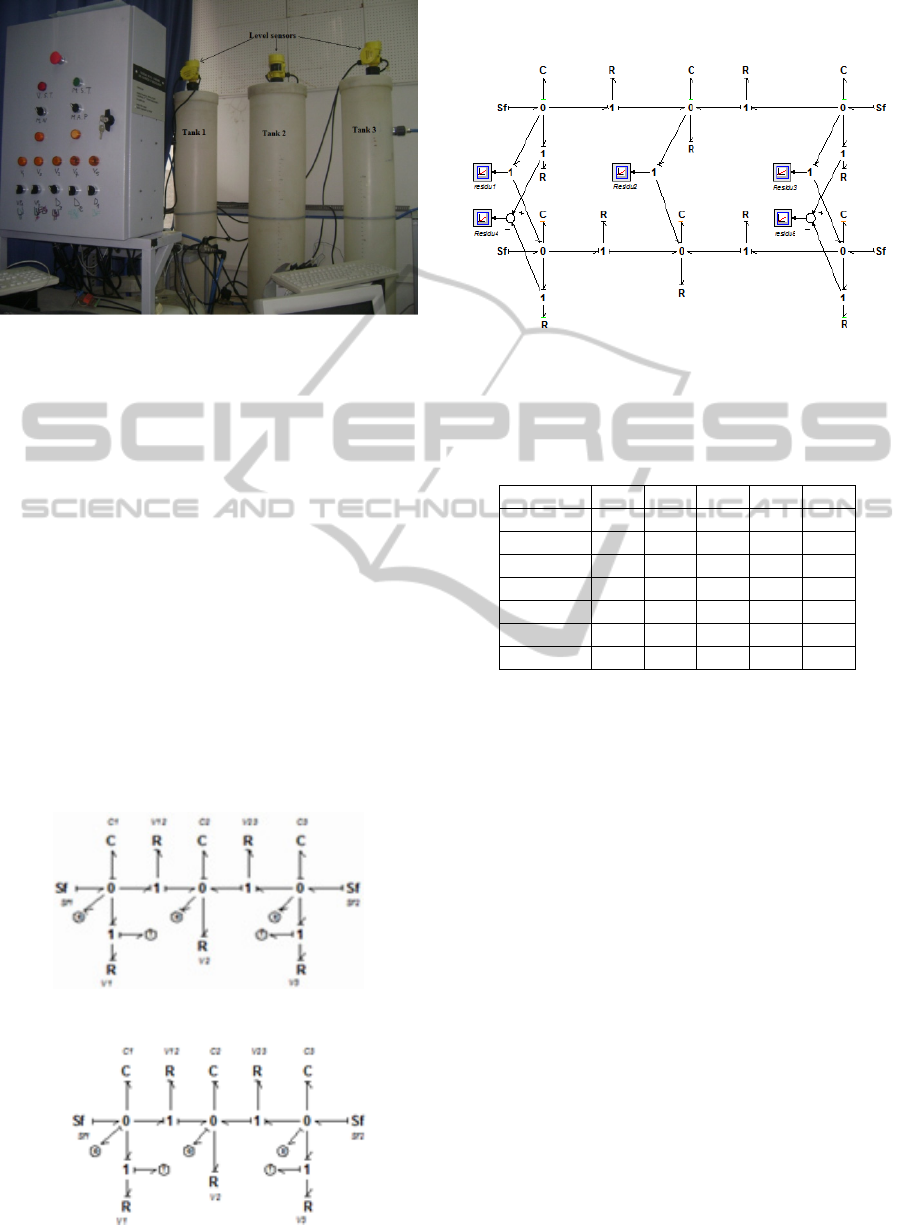
Figure 5: Real system.
This system is composed of three tanks T1, T2
and T3 respectively of diameters D1, D2 and D3;
water level in tanks, H1, H2 and H3 (proportional
respectively to the pressures P1, P2 and P3) is
measured by level sensors. This system is fed by two
pumps which deliver flows Sf1 (flow of entrance at
T1) and Sf2 (flow of entrance at T3).
Tanks T1 and T2 communicate through valve
V12 and tanks T2 and T3 through valve V23 of
diameter Sv. Each tank has a draining valve noted
Vi (i=1 to 3). Flow going out from valves V1 and
V2 is measured by flow sensors f1 and f2.
5.2 System BG Modelling
A procedure described in (Tagina, 1995) allows
elaborating the BG model of the system in integral
causality (Figure 6) as well as the corresponding
model in derivative causality (Figure 7).
Figure 6: BG model in preferred integral causality.
Figure 7: BG model in preferred differential causality.
The coupling between the two precedent models
produces the DBG of Figure 8:
Figure 8: DBG of the three tanks system.
From Figure 8, the following FSM can be
determined:
Table 2: Fault signature matrix of the three tanks system.
r1 r2 r3 r4 r5
Sf1 1 0 0 0 0
Sf2 0 0 1 0 0
V1 1 0 0 1 0
V12 1 1 0 0 0
V2 0 1 0 0 0
V23 0 1 1 0 0
V3 0 0 1 0 1
The supports of each residual deduced from the
DBG are given below:
C
1
:{Sf1, V1, V12}
C
2
:{V12, V2, V23}
C
3
:{Sf2, V23, V3}
C
4
:{V1}
C
5
:{V3}
6 EXPERIMENTAL RESULTS
6.1 Case of Normal Operating Mode
In Figure 9, different residuals in normal operating
mode are presented.
We notice that residuals have low values around
zero; this variation is due to parameters
uncertainties.
From Figure 9, we can deduce different
boundaries numeric values of the trapezoidal
memberships functions in the fuzzy detection
module. Different isolation methods were applied
with those boundaries. The results are given in
Figure 10. All the fault indexes of different methods
are equal to zero indicating that there are no faulty
CAUSAL REASONING IMPROVED BY FUZZY LOGIC FOR DIAGNOSIS OF BOND GRAPH MODELLED
UNCERTAIN PARAMETERS SYSTEMS
63

components.
Figure 9: Residuals evolution in normal operating mode.
Figure 10: Fault indexes with fault signature and
exoneration.
6.2 Case of Faulty Operating Mode
In case of faulty operating mode, some residuals
deviate from their normal values and isolation
methods are then used to identify the faulty
component.
6.2.1 First Case: Fault affecting Valve V12
We totally fill in valve V12 at time 5000s; Figure 11
illustrates the evolution of the different residuals.
We notice, at the occurrence of the fault,
residuals sensors r1 and r2 deviation; all the other
residuals do not exceed normal functioning
thresholds, the signature (1, 1, 0, 0, 0) is equivalent
to fault in component V12 (Table 2).
Figure 12 represents the fault indexes generated
by the fuzzy FSM method. We notice that fault’s
origin is perfectly identified. In fact, fault index
DefR12 passes to 1 at instant 5000s.
Figure 11: Residuals evolution in case of V12 fault.
Figure 12 represents the fault indexes generated
by the fuzzy FSM method. We notice that fault’s
origin is perfectly identified. In fact, fault index
DefR12 passes to 1 at instant 5000s.
Figure 12: Fault indexes with fault signature matrix.
The results of localization by exoneration
algorithm are shown in Figure 13. In this case, the
fault indexes of components SF1, V2 and V12
passed to 1 at time 5000s. Then, we obtain 3
candidates components: {SF1, V2, V12}.
Figure 13: Fault indexes with exoneration algorithm.
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-5
r1
Residuals variation
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-5
r3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r4
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r5
Time (s )
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defSF1
Fault indexes
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defSF2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defR1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defR2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defR3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defR12
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
-1
0
1
defR23
Time(s)
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-4
r1
Residuals' evolution
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-4
r2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-5
r3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r4
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r5
Time
(
s
)
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defSF1
Signature matrix
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defSF2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0
0.5
1
defR12
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR23
Time
(
s
)
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
0
0.5
1
defSF1
Exoneration
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
-1
0
1
defSF2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
-1
0
1
defR1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
0
0.5
1
defR2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
-1
0
1
defR3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
0
0.5
1
defR12
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
1
-1
0
1
defR23
Time
(
s
)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
64

6.2.2 Second Case: Fault Affecting Valve V3
We suppose that valve V3 is closed at instant 5000s,
Figure 14 presents the evolution of the different
residuals in this case.
Figure 14: Residuals evolution in case of V3 fault.
We notice that residuals r3 and r5 are affected by
this fault and make a distinctive variation from their
normal values. The signature (0, 0, 1, 0, 1)
represents fault in component V3 (Table 2)
In Figure 15, fault indexes obtained by signature
matrix method are shown. This method localizes
perfectly the faulty component (V3).
Figure 15: Fault indexes with fault signature matrix.
Localization indexes determined by exoneration
procedure are given in Figure 16. They identify two
candidates to the fault: SF2 and V3.
Figure 16: Fault indexes with exoneration algorithm.
7 CONCLUSIONS
In this paper, fuzzy logic approach and causal
properties of the BG model are combined for FDI.
The residuals generated from the DBG are processed
in the fuzzy detection module. Output is a fault
index indicating whether the residual is faulty or it is
in fault free case.
Causal properties of the BG model allow using 2
localization methods: FSM and exoneration
algorithm. Our principle criterion to judge proposed
methods performances is the false alarm rate. The
FSM has proved its superiority in case of single fault
hypothesis. Exoneration methods give a conflict set
composed of more than one element in most cases.
REFERENCES
Biswas, G., Koutsoukos, X., Bregon, A., Pulido, B.
(2009). Analytic Redundancy, Possible Conflicts, and
TCG-based Fault Signature Diagnosis applied to
Nonlinear Dynamic Systems, Proceedings of the
IFAC-Safeprocess, Barcelona, Spain.
Bouallègue, W., Bouslama Bouabdallah, S., Tagina, M.
(2010). Diagnosis of Bond Graph modelled uncertain
parameters systems using residuals sensitivity,
Proceedings of the IEEE International conference on
Systems, Man, and Cybernetics, Turkey, 593-600.
Bouslama Bouabdallah, S., Tagina, M. (2006). A fuzzy
approach for fault detection and isolation of uncertain
parameter systems and comparison to binary logic,
IFAC, IEEE 3rd International Conference on
Informatics in Control, Automation and Robotics,
ICINCO 2006. Portugal, Intelligent Control Systems
and Optimization, 98-106.
Cordier, M. O., Dague, P., Dumas, M., Levy, F.,
Montmain, J., Staroswiecki, M., and Trave-Massuyes,
L. (2004). Conflicts versus Analytical Redundancy
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-5
r1
Residuals' evolution
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
x 10
-5
r2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-4
r3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-2
0
2
x 10
-5
r4
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-5
0
5
x 10
-4
r5
Time (s)
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defSF1
Signature matrix
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defSF2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0
0.5
1
defR3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR12
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR23
Time (s)
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defSF1
Exoneration
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0
0.5
1
defSF2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR2
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0
0.5
1
defR3
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR12
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
-1
0
1
defR23
Time (s)
CAUSAL REASONING IMPROVED BY FUZZY LOGIC FOR DIAGNOSIS OF BOND GRAPH MODELLED
UNCERTAIN PARAMETERS SYSTEMS
65

Relations: a comparative analysis of the Model-based
Diagnosis approach from the Artificial Intelligence
and Automatic Control perspectives, IEEE Trans. on
Systems, Man, and Cybernetics (Part B), 34(5), 2163-
2177.
Dauphin-Tanguy, G. (2000). Les bond graphs, Hermès,
Paris.
Dauphin-Tanguy, G., Tagina, M. (2003). La méthodologie
bond graph: Principes et applications, Centre de
publications universitaires, Tunis.
Djeziri, M. A. (2007). Diagnostic des Systèmes Incertains
par l’Approche Bond Graph, Thesis, Ecole centrale of
Lille France.
Djeziri, M. A., Ould Bouamama, B., Merzouki, R. (2009).
Modelling and robust FDI of steam generator using
uncertain bond graph model, Journal of process
control.
Evsukoff A., Gentil S., Montmain J. (2000). Fuzzy
reasoning in co-operative supervision systems,
Control Engineering Practice, 389-407.
Frank, P. M., Köppen-Seliger. B. (1997). Fuzzy logic and
neural network applications to fault diagnosis,
International Journal of Approximate Reasoning,
Volume 16, Issue 1,67-88.
Fagarasan, I., Ploix, S., Gentil, S. (2004). Causal Fault
Detection and Isolation Based on a Set-Membership
Approach, Automatica, volume 40, 2099-2110.
Montmain, J., Gentil, S. (1999). Causal Modeling for
Supervision, Intelligent Control/Intelligent Systems
and Semiotics, Proceedings of the IEEE International
Symposium.
Samantaray A. K., Medjaher K., Ould Bouamama B.,
Staroswiecki M., Dauphin-Tanguy G. (2006).
Diagnostic bond graphs for online fault detection and
isolation. In Simulation Modelling Practice and
Theory.
Samantaray A. K., Ould Bouamama B. (2008). Model-
based Process Supervision: A Bond Graph Approach,
Springer.
Staroswiecki, M. (2000). Quantitative and qualitative
model for fault detection and isolation, Mechanical
Systems and Signal Processing, 2000.
Tagina, M. (1995). L'application de la modélisation bond
graph à la surveillance des systèmes complexes,
Thesis, University of Lille1, France 1995.
Venkatasubramanian, V., Rengaswamy, R., Kavuri, S. N.,
Yin, K. (2003.a). A review of process fault detection
and diagnosis Part I: Quantitative model-based
methods, Computers and Chemical Engineering 27,
293-311.
Venkatasubramanian, V., Rengaswamy, R., Kavuri, S. N.,
Yin, K. (2003.b). A review of process fault detection
and diagnosis Part II: Qualitative models and search
strategies, Computers and Chemical Engineering 27,
313-326.
Venkatasubramanian, V., Rengaswamy, R., Kavuri, S. N.,
Yin, K. (2003.c). A review of process fault detection
and diagnosis Part III: Process history based methods,
Computers and Chemical Engineering 27, 327-346.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
66
