A NEW PROPOSAL FOR A MULTI-OBJECTIVE TECHNIQUE

USING TRIBES AND SIMULATED ANNEALING

Nadia Smairi, Sadok Bouamama

National School of Computer Sciences, University of Manouba, 2010, Manouba, Tunisia

Khaled Ghedira, Patrick Siarry

High Institute of Management, University of Tunis, Tunis, Tunisia

University of Paris 12, LiSSi, E. A., 3956, Paris, France

Keywords: Particle Swarm Optimization, Tribes, Simulated Annealing, Multi-objective Optimization.

Abstract: This paper proposes a new hybrid multi-objective particle swarm optimizer which incorporates a particle

swarm optimization approach (Tribes) and Simulated Annealing (SA). The main idea of the approach is to

propose a skilled combination of Tribes with a local search technique based on Simulated Annealing

technique. Besides, we are studying the impact of the place where we apply local search on the performance

of the obtained algorithm which leads us to three different versions: applying SA on the archive’s particles,

applying SA only on the best particle among each tribe and applying SA on each particle of the swarm. In

order to validate our approach, we use ten well-known test functions proposed in the specialized literature of

multi-objective optimization. The obtained results show that using this kind of hybridization is justified as it

is able to improve the quality of the solutions in the majority of cases.

1 INTRODUCTION

Problems with multiple objectives present in a great

variety of real-life optimization problems. These

problems are generally involving multiple

contradictory objectives to be optimized

simultaneously. Therefore, the solution is different

from that of a mono-objective optimization problem.

The main difference is that they have a set of

solutions that are equally good. Thus multi-objective

optimization has been extensively studied during the

last decades. Several techniques are proposed: those

which are developed in the operational research field

but with great complexity and those based on meta-

heuristics that find approximate solutions. Among

these meta-heuristics, the Multi-Objective

Evolutionary Algorithms have been considered as

successful to deal with this kind of problems.

In the last years, the PSO is also adopted to solve

these problems, which is the approach considered in

the reported work in this paper. In fact, it consists on

the adaptation of Tribes, a parameter free algorithm

based on PSO to deal with multi-objective problems.

In fact, we propose in this paper, a skilled

combination of Tribes with a local search technique

which is SA in order to provide a more efficient

behaviour and higher flexibility when dealing with

the real world problems: SA is used to cover widely

the solution space and to avoid the risk of trapping in

non Pareto solutions and Tribes is used to accelerate

the convergence. In addition, we study the impact of

the place where we apply local search on the

performance of the algorithm which leads us to three

different versions. In our study, we use ten well-

known multi-objective test functions in order to find

the best one from the proposed techniques and to

justify the use of the local search.

2 TRIBES

2.1 Presentation

Tribes is a PSO algorithm that works in an

autonomous way. Indeed, it is enough to describe

the problem to be resolved and the way of making it

130

Smairi N., Bouamama S., Ghedira K. and Siarry P..

A NEW PROPOSAL FOR A MULTI-OBJECTIVE TECHNIQUE USING TRIBES AND SIMULATED ANNEALING .

DOI: 10.5220/0003538301300135

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 130-135

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

at the beginning of the execution. Then, it is the role

of the program to choose the strategies to be adopted

(Clerc, 2006).

2.2 Tribes Components

 The particle informer: A particle A is an

informer of a particle B, if B is capable of

reading the best position visited by A.

 The tribe: In the general case, a given particle

A can not inform the rest of the other particles

of the swarm. That’s why we define the tribe,

which is a subset of the swarm, where every

particle is capable of communicating directly

with the rest of the tribe’s particles.

 The swarm: it is formed by a set of tribes; each

one is looking to finding a local optimum. A

group of decisions is therefore necessary to

find the global optimum. For this reason, tribes

have to communicate between themselves.

 Quality of a particle: The notion of a good or

bad particle is relative to its tribe. We organize

particles, belonging to the same tribe according

to their fitness evaluations. As a result, we can

define the best particle and the worst particle

following every tribe.

 Quality of a tribe: to decide if a tribe T is good

or bad, we generate a random number t

between 0 and n (n being the size of T). If the

number of good particles is bigger than t, then

the tribe is considered as a good one.

Otherwise, the tribe is bad.

2.3 Tribe Evolution

The evolution of a tribe involves the removal or the

generation of a particle. The removal of a particle

consists in eliminating a particle without risking the

missing of the optimal solution. For that purpose,

only the good tribes are capable of eliminating their

worst elements. The creation of a particle is made

for bad tribes as they need new information to

improve their situations. However, we note that it is

neither necessary nor desirable to perform these

structural adaptations at each iteration because some

time must be allowed for the information to

propagate among the particles. Several possible rules

can be formulated to ensure this. The rule used is: if

the total number of information links is L after one

structural adaptation, then the next structural

adaptation will occur after L/2 iterations.

2.4 Swarm Move

The only remarkable difference between the

movements of the classic PSO algorithm and those

of Tribes is situated at the level of the probability

distribution of the next position which is modified; it

is D-spherical in the case of Tribes and

D-rectangular in the case of the classic PSO.

2.5 Swarm Evolution

At the beginning, we start with a single particle

forming a tribe. After the first iteration, the first

adaptation takes place and we generate a new

particle which is going to form a new tribe, while

keeping in touch with the generative tribe. In the

following iteration, if the situation of both particles

does not improve, then every tribe creates two new

particles: we form a new tribe containing four

particles. In this way, if the situation deteriorates,

then the size of the swarm grows (creation of new

particles). However, if we are close to an optimal

solution, the process is reversed and we begin to

eliminate particles, even tribes.

3 OUR APPROACH

3.1 Preliminary Study

In the multi-objective case, we have essentially to:

 Obtain a set of solution close to the true Pareto

front.

 Maintain the diversity within the found set.

For that purpose, several problems are detected:

 The choice of the informer of every particle.

 The choice of the best performance of every

particle.

 A remedy to the fact that Tribes can’t be

considered neither a local search technique nor

a global search one (Bergh, 2002).

The proposed solution to those problems consists in

using the Pareto dominance to respect the

completeness of every objective and to add an

external archive to save the found not dominated

solutions. Furthermore, the hybridization between

Tribes and a local search algorithm can be

considered as a competitive approach to handle

difficult problems of multi-objective optimization.

In order to improve the capacity of exploitation of

Tribes, we apply a local search technique: SA. In

fact, the local search is not going to be inevitably

applied in a canonical way that is on all the particles

A NEW PROPOSAL FOR A MULTI-OBJECTIVE TECHNIQUE USING TRIBES AND SIMULATED ANNEALING

131

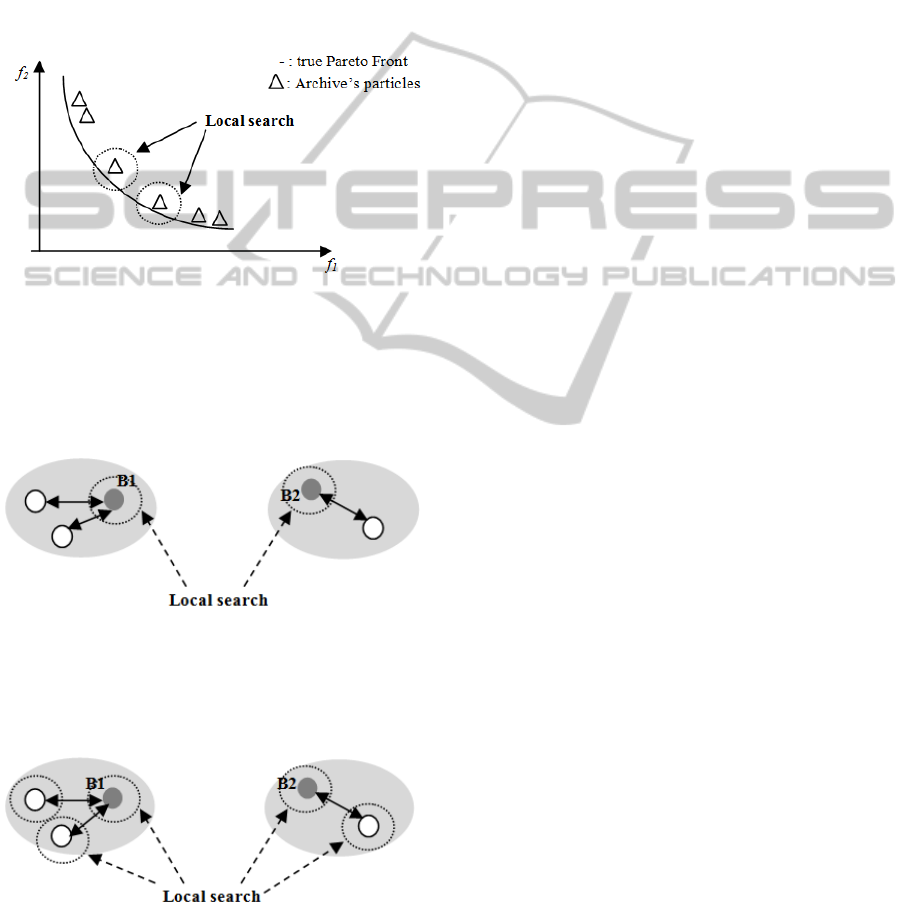
of the swarm: we also propose two other manners,

the first one consists in applying the local search

only among the best particle of every tribe. The

second one consists in applying it among the

particles of the archive. We shall have then three

versions of the algorithm.

The first one consists in applying the SA only to

the particles of the archive which are situated in the

least crowded zones. Let us note that, in this case,

the local search is not applied unless the archive is

full so that some time is allowed to the information

to propagate in the swarm.

Figure 1: SA-TribesV1.

The second version of the algorithm consists in

applying the SA only to the best particles of the

tribes. In fact, we consider that those particles are

situated in promising zones and probably they need

further intensification to find out other solutions.

Figure 2: SA-TribesV2.

The third version consists in applying the SA to

all the particles of the swarm. It is made at the

moment of the swarm adaptation.

Figure 3: SA-TribesV3.

3.2 Updating the External Archive

The update of the archive consists in adding all the

not dominated particles to the archive and deleting

the already present dominated ones. If the number of

particles in the archives exceeds a fixed number, we

apply a crowd function to reduce the size of the

archive and to maintain its variety. Indeed, Crowd

divides the objective space into a set of hypercube.

The role of the function Crowd is to give, for

every particle, the number of particles of the archive

which occupy the same hypercube.

In that case, when the addition of a particle to the

archive creates an overflow, we eliminate the one

who has the highest Crowd.

3.3 Choosing the Particle Informer

The choice of the particle informer is similar to the

case of mono-objective Tribes. Indeed, if we take a

particle which is not the best of its tribe, his guide is

then the best particle of the tribe. If we consider, on

the other hand, the best particle of a given tribe, the

informer is then some random particle from the

archive.

3.4 Hybridizing Tribes with SA

Simulated Annealing (SA) is a local search method

that accepts worsening moves to escape local

optimal. It was proposed originally by Kirkpatrick et

al. (1983), and it is based on an analogy with

thermodynamics, when simulating the cooling of a

set of heated atoms.

For use SA, a method for generation of an initial

solution, a method for generation of neighbouring

solutions and an objective function should be

defined.

However, SA is essentially intended for the

resolution of the combinatorial problems. Few works

considered its adaptation for the continuous

optimization. In our case, we are inspired from the

approach of Chelouah and Siarry (2000). In that

case, this method is similar to the classic SA. The

difference lies essentially in the generation of the

neighbourhood. It is necessary to define first of all a

way to discretize the search space. In fact, the

neighbourhood is defined by using the concept of

“ball”. A ball B(x, r) centered on x (current solution)

with radius r. To obtain a homogeneous exploration

of the space, we consider a set of balls centered on

the current solution x with radius r

, r

,…r

Hence the space is partitioned into concentric

crowns.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

132

The n neighbours of x are obtained by random

selection of a point inside each crown C

, for i

varying from 1 to n. Finally, we select the best

neighbour x ' even if it is worse than x.

Figure 4: Generating the neighbourhood.

4 EXPERIMENTATIONS AND

RESULTS

4.1 Test Functions

In order to compare the proposed techniques, we

perform a study using ten well-known test functions

taken from the specialized literature on evolutionary

algorithms. These functions present different

difficulties such as convexity, concavity,

multimodality …etc. The detailed description of

these functions was omitted due to space

restrictions. However, all of them are unconstrained,

minimization and have between 3 and 30 decision

variables. Indeed, we fix the maximal size of the

archive to 100 for the two-objective functions and to

150 to the three-objective ones. Moreover, we fix

the maximal number of evaluations in the

experimentations to 5e+4.

4.2 Metrics of Comparison

For assessing the performance of the algorithms,

there are many existent unary and binary indicators

measuring quality, diversity and convergence. In the

literature, there are many proposed combination in

order to perform a convenient study and comparison.

We choose the combination of two binary indicators

that was proposed in (Knowles, Thiele and Zitler,

2006): R indicator and hypervolume indicator.

4.3 Results

In order to validate our approach and to justify the

use of SA, we are going to compare those proposed

techniques against two other PSO-based-multi-

objective approaches representative of the state of

art: Mo-Tribes (Cooren, 2008) and adaptive MOPSO

technique (Zielinski and Laur, 2007). Moreover, we

compare them to multi-objective Tribes without

local search (Tribes-V4) in order to validate the use

of local search.

The binary indicators used to make the

comparison measure both convergence and

diversity. The results regarding the R indicator are

given in table 1 (R can take values between -1 and 1

where smaller values correspond to better results).

The hypervolume difference is given for all test

functions in table 2. Again, smaller values mean

better quality of the results because the difference to

a reference set is measured.

For both indicators, we present the summary of

the results obtained. In each case, we present the

average of R and hypervolume measures over 25

independent runs. These values are given for the

different sizes of neighbourhood.

According to these tables, we notice that the

adaptive MOPSO algorithm is giving the worst

results in comparison to the other techniques,

presumably because this algorithm presents a classic

PSO technique without sophisticated enhancements

used to handle the case of multi-objective

optimization. In fact, the proposed ameliorations are

used to control the parameters settings.

We notice also that the hybridization with the SA

gives generally better results than Tribes-V4.

Moreover, SA-TribesV1 outperforms generally the

others versions except for test functions S_ZDT4

and R_ZDT4 where SA-TribesV3 gives the best

results. In fact, at this case, a bad convergence

behaviour is detected for S_ZDT4 and R_ZDT4 for

all the versions except SA-TribesV3. We note that a

bad convergence behaviour is detected also with

another PSO algorithm for ZDT4 in (Hu, Eberhart

and Shi, 2003).

The results of Mo-Tribes are very close to those

of SA-TribesV1. This can be explained by the fact

that Mo-Tribes uses also a local search technique

applied only on the archive’s particles.

Finally, we recapitulate that SA-Tribes is very

competitive as it supports both intensification and

diversification. In fact, the choice of particle’s

informer is done in order to accelerate the swarm’s

convergence towards the search space zones where

are situated the archive’s particles. This can be

considered as an intensification process. Moreover,

the archive’s updating is done thanks to the Crowd

function that maintains the archive’s diversity. This

can be considered as a diversification process.

Indeed, SA supports both intensification and

diversification. The good neighbourhood exploration

A NEW PROPOSAL FOR A MULTI-OBJECTIVE TECHNIQUE USING TRIBES AND SIMULATED ANNEALING

133

Table 1: Results for R indicator.

Test

Functions

SA-TribesV1 SA-TribesV2 SA-TribesV3 Tribes-V4 MO-Tribes Adaptive-MOPSO

Oka2

-1

23e-3

-8

07e-5 -6

43e-4 8

51e-5 -1

10e-3 2

79e-2

art

08e-6

57e-5 8

12e-5 2

39e-4 5

18e-5 7

22e-5

SZDT1

27e-4

26e-3 6

43e-4 2

79e-3 5

12e-4 1

93e-2

SZDT2

07e-6

78e-3 5

32e-5 2

80e-4 5

01e-5 9

64e-2

SZDT4

86e-3 8

16e-3

74e-6

07e-3 4

96e-3 4

10e-2

RZDT4

24e-3 4

59e-3

16e-4

98e-3 5

23e-3 8

14e-3

SZDT6

96e-3

37e-3 3

84e-3 3

05e-3 3

51e-3 1

21e-1

WFG1

42e-2 6

72e-2 3

11e-2

22e-2

53e-2 7

68e-2

WFG8

-2

85e-2

-1

12e-2 -4

23e-3 -4

59e-4 -2

26e-2 -1

30e-2

WFG9

-2

14e-2

-3

60e-3 -7

52e-3 -5

06e-3 -9

10e-3 -6

78e-3

Table 2: Results for ܫ

ு

ഥ

indicator.

Test functions SA-TribesV1 SA-TribesV2 SA-TribesV3 Tribes-V4 MO-Tribes Adaptive-MOPSO

Oka2

-1,14e-3

-9,82e-4 -1,06e-3 -1,10e-4 -1,12e-3 5,54e-2

Sympart

1,23e-4

1,65e-4 1,97e-4 1,28e-4 1,52e-4 2,09e-4

S_ZDT1

6,49e-4

4,68e-3 5,12e-3 2,05e-3 2,25e-3 6,27e-2

S_ZDT2

3,15e-4

3,32e-3 3,74e-4 2,87e-4 3,38e-4 2,25e-1

S_ZDT4

6,71e-3 4,03e-2

2,51e-4

2,16e-2 2,12e-2 1,21e-1

R_ZDT4

2,16e-2 8,74e-3

1,07e-3

2,06e-2 1,55e-2 2,42e-2

S_ZDT6

1,01e-2 2,64e-2 1,60e-2 6,54e-2

7,41e-3

3,02e-1

WFG1

1,64e-1 1,97e-1 1,44e-1 3,44e-1

8,51e-2

3,88e-1

WFG8

-1,24e-1

-7,03e-2 -7,05e-2 -2,95e-2 -1,43e-2 -8,68e-2

WFG9

-2,83e-2 -2,12e-2 -4,17e-3 -3,28e-2

-5,72e-2

-3,86e-2

intensifies the search towards specific zones in the

search space. Besides, the SA mechanisms such as

accepting worsening moves allow avoiding the risk

of trapping in non Pareto solutions.

5 CONCLUSIONS

This work presented a new hybrid multi-objective

evolutionary algorithm based on Tribes and SA.

This hybrid aims to combine the high convergence

rate of Tribes with the good neighbourhood

exploration performed by the SA algorithm.

Therefore, we have studied the impact of the place

where we apply SA technique on the performance of

the algorithm. Two widely used metrics have been

used to evaluate the results. The proposed version

SA-TribesV1 gave the best results almost for all the

test functions except for S-ZDT4 and R-ZDT4 for

which the SA-TribesV3 gave the best results.

The results showed that the hybridization is a

very promising approach to multi-objective

optimization. However, for some complex problems

such as S-ZDT4 and R-ZDT4, SA-Tribes still need

to improve its performance. As part of our ongoing

work we are going to study some other strategies of

displacement and adaptation in order to remedy to

those problems.

REFERENCES

Bergh, F. (2002). An Analysis of Particle Swarm

Optimizers. PhD thesis, Departement of Computer

Science, University of Pretoria, Pretoria, South Africa.

Carlos, A. and Coello, C.A.C. (2000, June). An Updated

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

134

Survey of GA-Based Multiobjective Optimization

Techniques. ACM Computing Surveys, Vol. 32, No. 2.

Chelouah, R. and Siarry, P. (2000). Tabu Search applied

to global optimization. European Journal of

Operational Research 123, 256-270.

Clerc, M. (2006). Particle Swarm Optimization.

International Scientific and Technical Encyclopaedia,

John Wiley & sons.

Cooren, Y. (2008). Perfectionnement d'un algorithme

adaptatif d'optimisation par essaim particulaire.

Applications en génie médicale et en électronique.

PhD thesis, Université Paris 12.

Hu, X., Eberhart, R. and Shi, Y. (2003). Particle swarm

with Extended Memory for multi-objective

Optimization. In IEEE Swarm Intelligence

Symposium.

Kirkpatrick, S., Gellat, D.C. and Vecchi, M.P. (1983).

Optimization by simulated annealing. Science, 220:

671-680.

Knowles, J., Thiele, L. and Zitler, E. (2006, February). A

tutorial on the Performance Assessement of Stochastic

Multi-objective Optimizers. Tik-Report No-214,

Computer Engineering and Networks Laboratory,

ETH Zurich, Switzerland.

Zielinski, K. and Laur, R. (2007). Adaptive Parameter

Setting for a Multi-Objective Particle Swarm

Optimization Algorithm. Proceedings of the 2007

IEEE Congress on Evolutionary Computation, IEEE

Press, 3019 - 3026.

Zitzler, E. and Deb, K. (2007, July). Tutorial on

Evolutionary Multiobjective Optimization.

Proceedings of the Genetic and Evolutionary

Computation Conference (GECCO’07), London,

United Kingdom.

A NEW PROPOSAL FOR A MULTI-OBJECTIVE TECHNIQUE USING TRIBES AND SIMULATED ANNEALING

135