WHEELED MOBILE MANIPULATOR MODELING FOR TASK

PACE CONTROL

Gast´on H. Salazar-Silva

UPIITA, Instituto Polit´ecnico Nacional, Av. IPN 2580, Mexico City, D.F., Mexico

aime

Alvarez Gallegos

Secretar´ıa de Investigaci´on y Posgrado, Instituto Polit´ecnico Nacional, Mexico City, D.F., Mexico

Marco A. Moreno-Armend´ariz

Centro de Investigaci´on en Computaci´on, Instituto Polit´ecnico Nacional, Mexico City, D.F., Mexico

Keywords:

Robot control, Mobile robots, Robots kinematics.

Abstract:

Mobile manipulators have attracted a lot attention lately because they have many advantages over stationary

manipulator, such as larger a work space than a stationary manipulator could have in practice. However, the

proposed methods in the state of the art to obtain the kinematic model of a mobile manipulator are based in

modeling separately the mobile base and the manipulator arm, and later combining both models.

This paper shows a systematic approach to obtain the kinematic model of mobile manipulators that transforms

in the modeling problem of a stationary manipulator with non-holonomic kinematic constraints in the joints;

it is also showed an example of the application of the method, where the kinematic and dynamic models are

obtained with extensions of the same tools used in stationary robots.

1 INTRODUCTION

A mobile manipulator is a manipulator mounted on

a mobile robot; an example is a manipulator arm

mounted on a mobile robot with differential traction.

Mobile manipulators have many advantages over sta-

tionary manipulator, such as a larger work space. Mo-

bile manipulators can perform the tasks of locomotion

and handling; those tasks have been handled as two

separate problems, for example in (Wang et al., 2008)

the focus is on movement of the mobile base and in

(Joshi and Desrochers, 1986) the task is the motion of

the manipulator arm. However, recently there are lot

of attention to the performance of both tasks simulta-

neously, for example in (Mazur, 2010).

The problem of kinematic modeling of a mobile

manipulator has been attacked by obtaining sepa-

rately the kinematic models of the base and arm ma-

nipulator, and then combining both models (De Luca

et al., 2006). Due to the usefulness of mobile manip-

ulators, it is important to have methods and tools that

allow an easier analysis of the mobile manipulator.

This paper shows an integrated approach to the

kinematic modeling of wheeled mobile manipulators

that apply the same tools used in modeling stationary

robots. This method assumes that the mobile manipu-

lator is a stationary robot which have joints with non-

holonomic constraints; this approach allows the use

of existing tools to obtain the kinematic and dynamic

models, for example the Denavit–Hartenberg param-

eters and geometric Jacobians.

A kinematic modeling scheme for mobile manipu-

lators is presented in (Bayle et al., 2003; Mazur,2010)

where the kinematic models for the mobile platform

and the arm are determined separately. In (De Luca

et al., 2006) a method is presented for combining the

kinematic model of the mobile base with the station-

ary manipulator, but the mobile base and the manipu-

lator are still modeled with different methods. Partic-

ularly interesting example is in (Mazur, 2010), where

both the mobile base and the manipulator have non-

holonomic constraints and yet are modeled by differ-

ent methods.

The outline of this paper is as follows: the kine-

matic modeling of mobile robots is reviewed in Sec-

tion 2. The modeling method proposed in this report,

modeling the mobile manipulator simply as station-

ary manipulators with joints that have kinematic con-

313

H. Salazar-Silva G., Álvarez Gallegos J. and A. Moreno-Armendáriz M..

WHEELED MOBILE MANIPULATOR MODELING FOR TASK SPACE CONTROL.

DOI: 10.5220/0003540203130316

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 313-316

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

straints, is presented in Section 3. In Section 4 a con-

trol for task space is proposed. As an example of the

method, in Section 5 the kinematic and dynamic mod-

els of a 5-degree of freedom (DOF) mobile manipula-

tor are obtained and the implementation of the control

presented in Section 4 is done.

2 KINEMATIC MODEL OF

MOBILE ROBOT

A kinematic model describes the relationship between

the motion of a mechanical system and the actuation

velocities. The motion of a wheeled mobile robot

is characterized by the constraints imposed by the

wheels (Campion et al., 1996); in this section it is

brieﬂy reviewed the issues on kinematic constraints

and the development of kinematics models.

A set of k kinematic constraints restricts the mo-

tion of a mechanical system and can be expressed as

(q, ˙q) = 0,

where q ∈ R

is the conﬁguration variables vector, ˙q∈

is the conﬁguration velocities vector and n is the

size of the conﬁguration vector, usually called degree

of freedom (DOF), a

are scalar functions on q and

˙q. If the function a

does not depend on ˙q then the

system is called holonomic, otherwise it is said that

the system is nonholonomic.

There are two kinds of kinematic models as pro-

posed in (Campion et al., 1996). The ﬁrst is the pos-

ture kinematic model and is a relationship between

the motion on the task space and the motion of the ac-

tuators; for a wheeled mobile robot with differential

traction it can be expressed as (Campion et al., 1996)

˙r

(t) = B

(q)η

(1)

where ˙r

(t) ∈ R

are the posture velocities on a task

space of dimension p, η

(t) ∈ R

n−k

is the vector

which contains the velocities of the actuators, and

(q) ∈ R

n×(n−k)

is a matrix with its columns are

a base of the null space of the nonholonomic con-

straints.

On the other hand, the conﬁguration kinematic

model is the relationship between the velocities of the

joints variables and the velocities of the actuators and

it is deﬁned as

˙q

(t) = S

(q)η

(2)

where S

(q) ∈ R

n×(n−k)

is a matrix with its columns

are also a base of null space of the constraints. It is

also important to note that S(q) is an annihilator of the

kinematic constraints, such that

A(q)

(q) = 0; (3)

this fact can be used to simplify the dynamic model

(De Luca and Oriolo, 1995).

3 MOBILE MANIPULATOR

MODELING

The kinematics of a mobile manipulator is given by

the function f, deﬁned as

r = f(q) (4)

where r is the combined posture of the mobile manip-

ulator and q are the combined generalized coordinates

of the mobile base and the manipulator arm; Thus the

kinematic modeling of a mobile manipulator depends

on ﬁnding the Jacobian J,

J =

∂

∂q

f(q) (5)

and which depends in turn on combining the kinemat-

ics of the manipulator and the base mobile.

A method to ﬁnd the direct kinematics of the

manipulator arm and mobile base, and also allows

combine them, are the homogeneous transformations;

speciﬁcally for the mobile manipulator it is deﬁned as

(Li and Liu, 2004):

= T

where T

is the homogeneous transformation which

goes from a frame {b} ﬁxed on the mobile base to

a frame {0} ﬁxed on surface on which the mobile

base moves, and T

is the homogeneous transforma-

tion which goes from a frame {n} ﬁxed on the last

link of the mobile manipulator to the frame {b}; there

is not a standardized method to ﬁnd the transforma-

tion T

. It is important to remark that T

does not

take account of the nonholonomic constraints.

The proposed method is to obtain the forward

kinematics of the mobile base T

by assuming that the

mobile base is stationary manipulator of b DOF and

considering it a unique kinematic chain, and the ap-

plying a modeling method for stationary robots, such

as the Denavit–Hartenbergmethod. Also it is possible

to obtain the Jacobian J of the whole mobile manipu-

lator from the same geometric method used in station-

ary robots and then is possible to obtain the posture

kinematic model of mobile manipulator

˙r = B(q)η (6)

where η is the vector of the actuation variables and is

deﬁned as

η =



˙q



ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

314

B(q) is the posture kinematic relation of the mobile

manipulator, deﬁned as

B(q) = J(q)S(q)

S(q) is the conﬁguration kinematic relation for the

whole mobile manipulator

S(q) =



(q) I



where I is a identity matrix, showing that the conﬁg-

uration velocities are identical to the actuation veloci-

ties. Some advantages of the proposed method is that

uses the same methods and computational tools as the

stationary manipulators to obtain the kinematic mod-

els.

4 CONTROL IN TASK SPACE

The control proposed in this paper follows the classi-

cal combination of two control loops in cascade; the

internal loop control uses an inverse dynamics con-

trol. The external control loop is a resolution of ac-

celeration control over the task space. The dynamic

model of a mechanical system with non-holonomic

constraints is deﬁned by a set of n second-order dif-

ferential equations

D(q) ¨q+C(q, ˙q) ˙q+ g(q) = A(q)λ+ S(q)τ

A(q)

˙q = 0

(7)

where D(q) ∈ R

n×n

is the inertia matrix for the

system, C(q, ˙q) ∈ R

n×n

is the Coriolis and cross-

velocities matrix, g(q) ∈ R

is a vector which repre-

sents the impact of gravity on the links, A(q) ∈ R

n×k

is a matrix in which k kinematics constrains are ex-

pressed, S(q) ∈ R

m×n

in the input matrix, and τ ∈ R

are the generalized forces that go into system.

Taking advantage of (3), it is possible to eliminate

the explicit statement of the kinematic constraint in

(7) by applying (1), thus the following reduced order

system is obtained (De Luca and Oriolo, 1995)

˙q = S(q)η

η = −M(q)

−1



m(q,η) + S(q)

S(q)τ



(8)

where

M(q) = S(q)

D(q)S(q)

m(q,η) = S(q)



D(q)

Sη+C(q,Sη)Sη + g(q)



A control τ is proposed such that it cancels the dy-

namics in (8)

τ = (S(q)

S(q))

−1

m(q,η) + (S(q)

S(q))

−1

Ma (9)

where a(t) ∈ R

is the acceleration reference for the

system.

For the external control loop, the resolution of ac-

celeration control (RAC) is used. Firstly, a measure

of the error on task space is proposed, ˜r, such that

˜r(t) = r

(t) − r(t).

where r

(t) ∈ R

is the desired posture. The control

is then proposed according to the following error dy-

namics

˜r(t) + K

˜r(t) = 0 (10)

where

˜r and

˜r are the ﬁrst and second derivatives of

the error with respect time. Then (10) in combination

with (2) are used to obtain

η = B(q)

†



¨r

−

B(q,η)

η+ K

˜r+ K

˜r



. (11)

5 EXAMPLE

To test the proposed method, a mobile manipulator

was modeled; it is integrated by a diferential-traction

Pioneer 3DX mobile robot and a Cyton manipulator

arm with 7 DOF, but only two joint were considered,

thus the mobile manipulator has 5 DOF. It is assumed

that the mobile base is a unicyclewithout slipping and

the surface on which the mobile base moves is ﬂat

and horizontal. The mobile manipulator was numeri-

cally modeled with the Matlab’s

robotics toolbox

(Corke, 1996).

The mobile manipulator was modeled as a station-

ary manipulator, as shown in Figure 1. The Denavit–

Hartenberg parameters are showed on Table 1. The

conﬁguration of the mobile manipulator, q(t), is de-

ﬁned as:

q =





Table 1: The Denavit–Hartenberg parameters for the 5-DOF

mobile manipulator.

i α a θ d Kinematic

[mm] [mm] pair

1 −π/2 0 0 0 prismatic

2 π/2 0 −π/2 0 prismatic

3 0 0 0 237 revolute

4 0 150 0 0 revolute

5 0 168 0 0 revolute

where d

, d

are the surface coordinates (x,y) of the

mobile base, θ

= φ is the orientation of the mobile

base, and θ

, θ

are the joint variables of the manipu-

lator arm.

On the other hand, the kinematic constraint of the

5-DOF mobile manipulator is given by the matrix

A(q) ∈ R

5×1

and it is deﬁned by the expresion

A(q) =



sinq

−cosq

0 0 0



. (12)

WHEELED MOBILE MANIPULATOR MODELING FOR TASK SPACE CONTROL

315

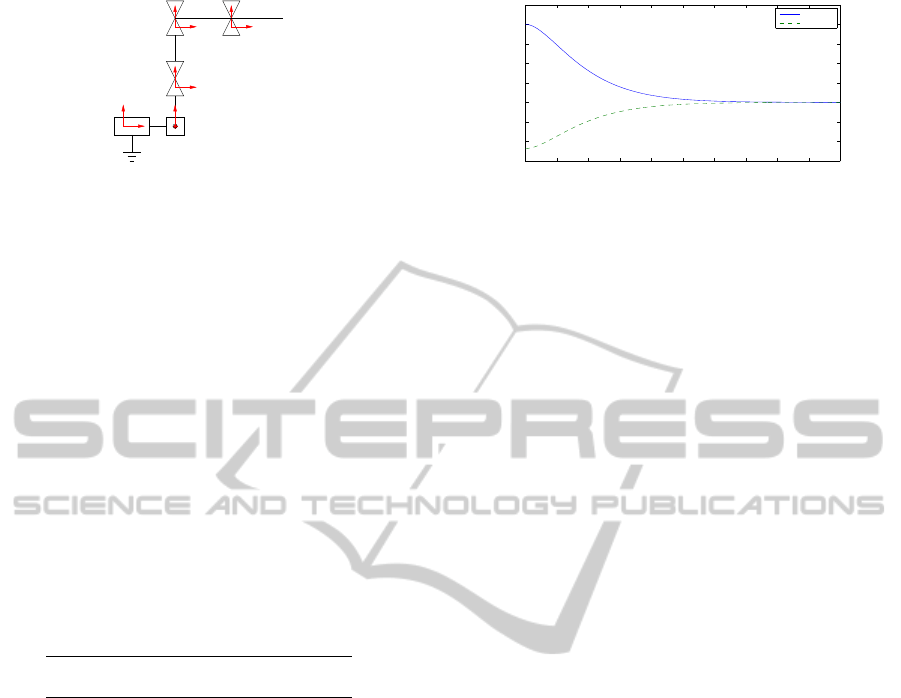
Figure 1: Kinematic representation of a mobile manipulator

5 DOF.

The actuators velocities, η ∈ R

, are deﬁned as:

η = (v, ˙q

, ˙q

)

where v(t) is an scalar which describes the lineal ve-

locity of the mobile robot, and conﬁguration kine-

matic model S(q) ∈ R

5×4

is deﬁned by

S(q) =







cosq

0 0 0

sinq

0 0 0

0 1 0 0

0 0 1 0

0 0 0 1







(13)

which satisfy the property of being an annihilator for

(12). The parameters of (7) are obtained according to

(Spong et al., 2006) and the data that appears in Table

Table 2: Link data for dynamic model from the 5-DOF mo-

bile manipulator.

i Length Wide Height Mass

[mm] [mm] [mm] [kg]

3 445 393 237 9.0

4 150 50 50 0.1

5 168 50 50 0.1

The control described in Section 4 was applied to

a numerical model of the mobile manipulator. The

result of the simulations are showed in Figure 2; the

reference is a trajectory in task space generated by a

linear interpolation between two points; it is impor-

tant to note that the trajectory not necessarily satisfy

the nonholonomic constraint.

6 CONCLUSIONS

This paper shows a systematic approach to model-

ing mobile manipulators that transforms the problem

to the modeling of a stationary manipulator station-

ary with non-holonomic kinematic constraints on the

joints. It is also presented a control that uses an esti-

mate of the derivative of the posture kinematic model.

Finally, an example is presented using this method.

In future work, it will develop a priority control in

the task space for a mobile manipulator, and it will be

develop a teleoperation scheme on the real system.

0 1 2 3 4 5 6 7 8 9 10

−0.15

−0.1

−0.05

0.05

0.1

0.15

0.2

0.25

Time [s]

Error [m]

Error on x

Error on y

Figure 2: Posture error graph for the mobile manipulator

under the control, as described in Section 4.

ACKNOWLEDGEMENTS

The authors appreciate the support of Mexican Gov-

ernment (SNI, SIP-IPN, COFAA-IPN, PIFI-IPN and

CONACYT).

REFERENCES

Bayle, B., Fourquet, J.-Y., and Renaud, M. (2003). Kine-

matic modelling of wheeled mobile manipulators. In

Robotics and Automation, 2003. Proceedings. ICRA

’03. IEEE International Conference on, pages 69–74.

Campion, G., Bastin, G., and Dandrea-Novel, B. (1996).

Structural properties and classiﬁcation of kinematic

and dynamic models of wheeled mobile robots. IEEE

Trans. Robot., 12(1):47–62.

Corke, P. (1996). A robotics toolbox for MATLAB. IEEE

Robotics and Automation Magazine, 3(1):24–32.

De Luca, A. and Oriolo, G. (1995). Kinematics and Dy-

namics of Multi-Body Systems, chapter Modelling and

control of nonholonomic mechanical systems, pages

277–342. Springer.

De Luca, A., Oriolo, G., and Giordano, P. R. (2006). Kine-

matic modeling and redundancy resolution for non-

holonomic mobile manipulators. In Proceedings of

the 2006 IEEE International Conference on Robotics

and Automation, pages 1867–1873, Orlando, Florida,

USA.

Joshi, J. and Desrochers, A. (1986). Modeling and con-

trol of a mobile robot subject to disturbances. In Pro-

ceedings of the 1986 IEEE International Conference

on Robotics and Automation, pages 1508–1513.

Li, Y. and Liu, Y. (2004). Control of a mobile modular ma-

nipulator moving on a slope. In Mechatronics, 2004.

ICM ’04. Proceedings of the IEEE International Con-

ference on, pages 135–140.

Mazur, A. (2010). Trajectory tracking control in workspace-

deﬁned tasks for nonholonomic mobile manipulators.

Robotica, 28:1–12.

Spong, M. W., Hutchinson, S., and Vidyasagar, M. (2006).

Robot Modeling and Control. Wiley.

Wang, Y., Lang, H., and de Silva, C. W. (2008). Visual servo

control and parameter calibration for mobile multi-

robot cooperative assembly tasks. In IEEE Interna-

tional Conference on Automation and Logistics, 2008.

ICAL 2008, pages 635–639, Qingdao.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

316