
CROSSLINKING BY PEROXIDE AND SULPHUR
VULCANIZATION: CHEMICAL MECHANISMS
AND REACTION KINETIC DETERMINATION
A Comprehensive Numerical Model
Gabriele Milani
Technical University of Milan, Piazza Leonardo da Vinci 32, 20133, Milan, Italy
Federico Milani
CHEMCO Consultant, Via J. F. Kennedy 2, 45030, Occhiobello, Rovigo, Italy
Keywords: Vulcanization, Kinetic model, Peroxides, Accelerated sulphur, Crosslinking, Mathematical model.
Abstract: The work presents a comprehensive numerical model to optimize mechanical properties of thick rubber
vulcanized items, comprising medium and high voltage electric cables and 3D devices. Several
vulcanization systems are considered, including peroxides and accelerated sulphur. In the case of peroxides,
both a genetic algorithm (GA) with zooming and elitist strategy and an alternating tangent (AT) approach
are adopted to determine the optimal final mechanical properties (tensile strength) of 2D and 3D rubber
items. The use of a mixture of peroxides is also taken into account, demonstrating that it helps in reducing
the curing time and/or in increasing the optimal tensile strength in both core and skin of thick devices. For
sulphur vulcanization, a mathematical kinetic model is presented to accurately predict the crosslinking
density of vulcanized rubber. It bases on the actual reactions occurring in practice and allows to estimate the
overall degree of vulcanization of real manufactured items.
1 INTRODUCTION
The matter of vulcanizing adequately thick rubber
items has been in the recent past largely under-
investigated, since the utilization was limited to
items with thicknesses not exceeding 5 mm. The
need of producing rubber insulators for medium and
high voltage electric cables have made critical the
problem of obtaining a sufficient vulcanization level
for thick items. As a matter of fact, for thick objects,
the skin results usually over-vulcanized whereas the
core remains essentially under-vulcanized.
Considering that the final mechanical properties
(elastic and inelastic) of the items are strongly
dependent on the degree of vulcanization, it can be
argued that the optimization of the vulcanization
production parameters (temperature and exposition
time) is critical. In particular, it has been widely
shown that final vulcanized rubber mechanical
properties (elastic modulus, tension set, tensile
strength, tear resistance, etc.) depend on the degree
of vulcanization.
In this framework, this paper presents a
comprehensive numerical model to optimize
mechanical properties of thick rubber vulcanized
items, comprising medium and high voltage electric
cables and 3D devices. Both peroxides and
accelerated sulphur vulcanization systems are
considered. In the case of peroxides, both a genetic
algorithm (GA) with zooming and elitist strategy
and an alternating tangent (AT) approach are
adopted to determine the optimal final mechanical
properties (tensile strength) of 2D and 3D rubber
items. The use of a mixture of peroxides is also
taken into account, demonstrating that it helps in
reducing the curing time and/or in increasing the
optimal tensile strength in both core and skin thick
items. While for peroxides the decomposition kinetic
is known, and hence the reticulation level is directly
dependent on the quantity of decomposed peroxide,
for accelerated sulphur a comprehensive kinetic
87
Milani G. and Milani F..
CROSSLINKING BY PEROXIDE AND SULPHUR VULCANIZATION: CHEMICAL MECHANISMS AND REACTION KINETIC DETERMINATION - A
Comprehensive Numerical Model.
DOI: 10.5220/0003543000870092
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
87-92
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
model is still missing, Kresja & Koenig (1993). At
this aim, for sulphur vulcanization, a mathematical
kinetic model is presented to accurately predict the
crosslinking density of vulcanized rubber. Unknown
parameters of the model are numerically fitted
through experimental cure curves provided by the
rotor-less cure-meter RPM 2000 (ASTM D 5289)
and/or rotor cure-meter (ASTM D 2084-81).
2 HEAT EXCHANGE MODEL:
GOVERNING PARTIAL
DIFFERENTIAL EQUATIONS
Temperature profiles for each point of a generic item
can be obtained solving numerically a differential
equation field problem representing Fourier’s heat
equation law, which, in its general form, may be
written as:
0
2
rpp
p
pp
HrT
t
T
c
(1)
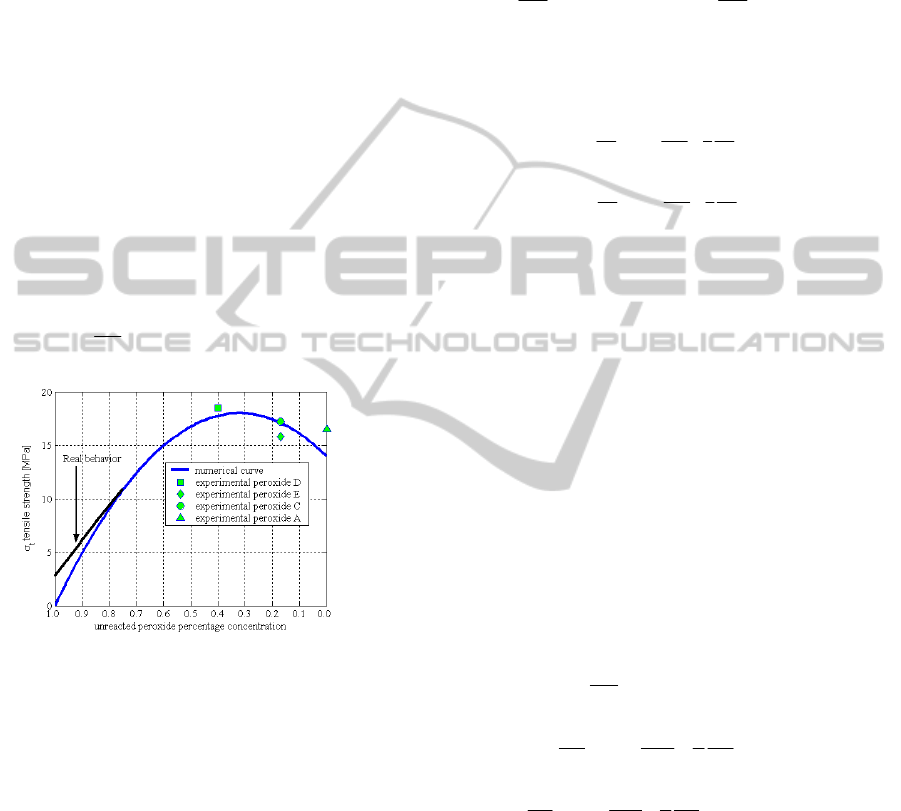
Figure 1: Non-linear behaviour of final tensile strength of
an item with respect to unreacted peroxide concentration.
Where
p
is the coefficient of thermal
conductivity,
p
p
c
is the specific heat,
p
is rubber
density,
r
H
is rubber specific heat (enthalpy) of
reaction,
p
r
is the rate of cross-linking. The term
rp
Hr
in equation (1) is the heat required by the
decomposition of the peroxide during peroxidic
crosslinking.
r
H
usually ranges from 120 to 180
kJ/mo
. From a technical point of view, the final
tensile strength of a vulcanized item does not
increase linearly with the curing time, but it passes
from a maximum as shown in Figure 1.
Optimal
T
ˆ
curves (expressed as implicit
functions in cure temperature
c
T
and
t
) can be
deter-
mined solving point by point the following
optimization problem:
max
max
11
0
0
tosubject
,
1
maxor,
1
max
tt
TT
tTF
N
tT
N
i
c
i
c
N
k
ii
c
k
t
L
N
k
ii
c
k
t
L
LL
conditionsinitialandboundary
0
1
0
1
systemPDEs
2
2
2
2
rpp
p
pp
j
p
jj
Hr
r
T
r
r
T
t
T
c
r
T
r
r
T
t
T
c
(2)
Where
L
N
is the number of layers in which the
insulator thickness is subdivided,
k
is the
k
-th
layer and
max
c
T
(
max
t
) is an upper bound limitation
for cure temperature (exposition time).
Two dedicated distinct models have been
developed and tested by the authors to solve (2), see
Milani & Milani (2008, 2009, 2010a) for algorithm
details. The first one is a non-standard genetic
algorithm (GA), whereas the second is an alternating
tangent approach (AT), described in detail hereafter.
When an expensive grid procedure is used, for
each point
ji
c
ji
tTP ,
,
of the grid, a mixed
algebraic-PDEs system is numerically solved by
means of the finite element method:
L
N
k
ji
c
k
t
L
t
tT
N
1
,
1
0
1
2
2
r
T
rr
T
t
T
c
j
p
jj
0
1
2
2
rpp
p
pp
Hr
r
T
r
r
T
t
T
c
+ initial and boundary conditions
(3)
2.1 Peroxidic Vulcanization
For EPM/EPDM the following peroxides are
ordinarily used (commercial names by Akzo):
Trigonox 101 (t
1/2
=0,1h at 171°C)(E), Perkadox BC
(t
1/2
=0,1h at 162°C)(C), Trigonox 29 (t
1/2
=0,1h at
138°C)(A) and Perkadox 14 (t
1/2
=0,1h at 169°C)(D).
As well known, peroxides decomposition kinetic is
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
88

of first order, i.e.
k
C
dtdC
/
. Peroxides follow the
Arrhenius equation and hence the reaction constant
is ruled by:
TR
E
g
a
eKTK
(4)
Where
K
and
a
E
are the only two constants to be
determined that define completely the behaviour of
the peroxide at different temperatures. Once known
2/1
t
at a given temperature, it can be easily shown
that:
TR
E
TR
E
g
a
g
a
eTtTt
~
2/12/1
/
~
(5)
Producers furnish, for each commercial peroxides,
values of
K
and
a
E
or, alternatively curves of
2/1
t
at different temperatures.
-a -b
-c
Figure 2: High voltage electric cables (green squares
represent GA optimization points). Cure time-
temperature-tensile strength surfaces. –a: di-cumyl-
peroxide C. –b: peroxide A. –c: peroxide D.
2.2 GA Numerical Results
In Figure 2-a,b,c rubber mean tensile strength at
different temperatures and exposition times is
reported for high voltage cables, assuming as
reticulation inducer three different peroxides. The
3D surface is obtained by means of the iterated
solution of problem (3 on an expensive regular grid
of points, whereas green squares represent the GA
best fitness points. As it is possible to notice, the
algorithm proposed is able to reach tensile maximum
strength with sufficient accuracy for all the
simulations performed.
A detailed comparison among all the results
underlines that peroxide choice is crucial. Each
peroxide, in fact, exhibits a different
0,
ˆ
tTT
c
behavior; in some cases, optimal curves
T
ˆ
are
sensibly different resulting in completely different
production line parameters to select during design.
For engineering interest, we have made
additional numerical simulations on realistic 3D
items using again the above GA, but with mixtures
of peroxides, with the aim optimizing again the
curing time and the tensile strength.
When a total initial concentration
0
C
of two
peroxides is present in the mixture, we assume that
each peroxide decomposes separately, following a
first order differential equation. Indicating with
index 1 and 2 peroxide 1 and 2 respectively and with
21
CCC
the sum of peroxides unreacted
concentrations, we obtain:
2211
21
22
2
11
1
CkCk
dt
CCd
Ck
dt
dC
Ck
dt
dC
(6)
Figure 3: Temperature profile of 3D item at
CT
c
160
. –
a: 6000 seconds. –b: 2500 seconds.
Obviously, during vulcanization,
tTT
and
therefore a numerical integration is needed for each
point of the items to vulcanize. In particular, a Finite
Element FEM approach (Evans et al. 2001) is used
to solve the 3D heat transmission problem. In order
to have an insight into this phenomenon, in Figure 3
temperature patches for a 3D docks bumper (only ¼
of the mesh is shown) are represented at 6000 and
2500 seconds, assuming
c
T
=160°C and highlighting
two different nodes with colored dots (one is a node
near the external surface, whereas the other belongs
to the internal core). In the simulations, a 50%-50%
percentage of Peroxide A and E is used.
Temperature-time, residual peroxides
concentration vs time and tensile strength diagrams
for the two nodes are reported in Figure 4, assuming
a curing time equal to 4400 seconds. As it is possible
CROSSLINKING BY PEROXIDE AND SULPHUR VULCANIZATION: CHEMICAL MECHANISMS AND
REACTION KINETIC DETERMINATION - A Comprehensive Numerical Model
89
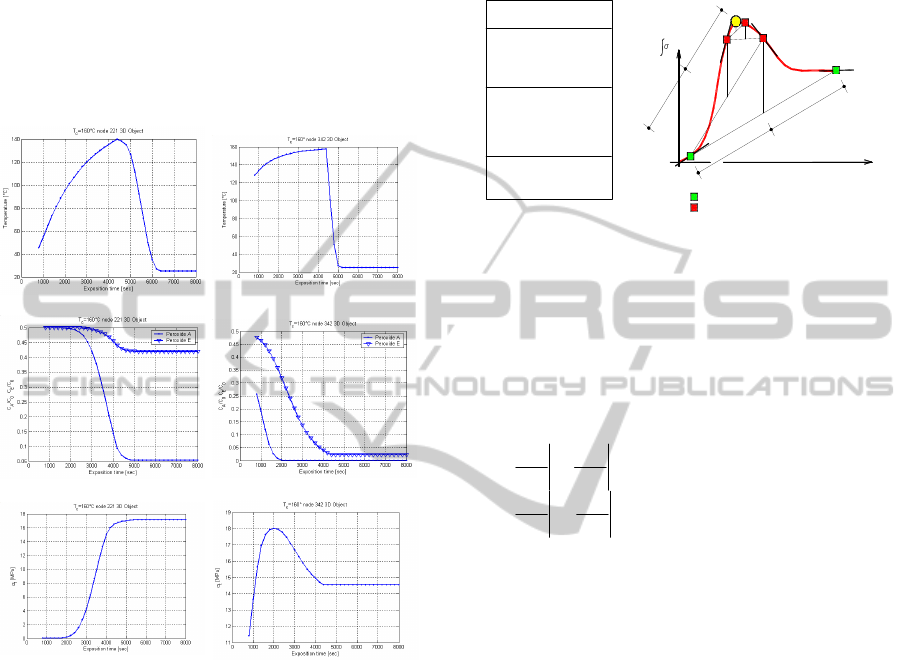
to notice, Point A reaches a good level of
vulcanization (Figure 4-c left), which is also
addressed by the residual unreacted concentration of
one of the two peroxides (Figure 4-b left). On the
contrary, Point B results over-vulcanized (Figure 4
right), meaning that both peroxides residual
concentration is negligible. As one can note, it is
particularly evident the difference in the resulting
tensile strength at the end of the vulcanization
process.
Point A Point B
-a
-b
-c
Figure 4: Point a & b response. (-a)
t
-
T
, (-b)
t
-peroxide
concentration and (-c)
t
-
t
curves. In the case analyzed
5.0
.
2.3 Alternating Tangent Approach (AT)
The AT approach used in the case of the 3D item is
based on the numerical evaluation of tensile strength
first derivatives with respect to exposition time on
several sections at fixed curing temperatures T
c
and
in the iterated bisection of a determined exposition
time search interval.
At a fixed T
c
temperature, Figure 5, tensile
strength is evaluated on two starting points (points 1
and 2), usually placed at a very under-vulcanized
and a very over-vulcanized exposition time. First
derivatives
dtd
t
/
of tensile strength with respect to
exposition time are needed at the search interval
extremes and are determined through finite
differences.
Middle point first derivative of the search
interval is also needed.
Figure 5: Alternating tangent approach (AT) basic scheme.
Once that first derivatives are at disposal on the
search interval extremes and on the middle point, a
bisection procedure is adopted, reducing the search
interval to one-half. In particular, the new interval is
respectively the right or the left one half depending
on the sign of first derivatives of the extremes with
respect to the middle point one:
intervalsemileft0if
intervalsemiright0if
32
31
dt
d
dt
d
dt
d
dt
d
tt
tt
(7)
The procedure is repeated on the new reduced
interval, until a desired degree of accuracy is
obtained (yellow circle in Figure 5).
3 SULPHUR VULCANIZATION
Sulphur vulcanization chemistry is somewhat
complex and has not been well understood
throughout the century of the practice of the process
since its discovery by Goodyear (1844). In
particular, because of the prohibitive complexity of
the reactions induced by sulphur during crosslinking
-differently to peroxidic curing- no precise reaction
kinetics formulas are available in the technical
literature. However, for EPDM, the basic reactions
involved are commonly accepted to be the
following:
f
v
K
ve
K
vx
K
vv
KK
PPDPQPPPPAP
edcba
54321
*
1
*
1
)()()()()(
(8)
Where the symbols have the following meaning:
-
P
and
A
are the polymer (EPDM) and soluble
sulphureted zinc complex(S8 + accelerators +ZnO +
Step 0: evaluate first
derivative at points 1 and 2
1
2
Step 1: evaluate first
derivative at point 3 (mean
value between abscissae 1
and 2)
3
Step 3: select the new
extreme of the interval on
the bases of the sign of 3
first derivative (negative
1-3 positive 3-2)
4
Step 4: repeat Step 1
substituting original points
with the new extremes
5
Optimal point
Curing time t
t
t
Starting extremes
Extremes at successive iterations
L
L
L
'
L
'
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
90
stearic acid) respectively;
*
1
P
is the pendent sulphur
(crosslink precursor);
v
P
is the reticulated EPDM;
f
v
P
,
x
Q
and
e
D
are the matured cross-link, the
oxidation product and diaryl-disulphide respectively,
5,...,1
K
are kinetic reaction constants, which depend
only on reaction temperature.
Here it is worth noting that reaction (a) in (8)
represents an allylic substitution, reaction (b) is the
disproportionation, whereas reactions (c) (d) and (e)
occurring in parallel are respectively the oxidation,
the de-sulphuration and the de-vulcanization.
From a practical point of view, it is commonly
accepted that the variation of the cure-meter curve,
intended as the progressive increase of rotor
resistance during vulcanization, characterizes
macroscopically the rubber reticulation level.
3.1 Kinetic Model Proposed
Chemical reactions occurring during sulphur
vulcanization reported in Milani & Milani (2010b,
2011a and 2011b) obey the following rate equations:
v
v
v
e
v
x
vex
v
PK
d
t
dP
e
PK
dt
dD
d
PK
dt
dQ
c
PKDKQKPK
dt
dP
b
APK
dt
dP
a
f
f
5
4
3
543
*
12
1
(9)
Differentiating equation (9), after several trivial
arrangements, reticulation law can be written as:
APKK
dt
dP
KPK
dt
dP
K
dt
Pd
v
vv
212
2
2
2
2
~
(10)
being
2
5
2
4
2
35432
2
~
KKKKKKKK
.
The solution of (10) turns out to be:
tPK
tt
v
eKPKKPKPKK
eCeCtP
01
1
2
012
2
01
2
021
21
~
(11)
Provided that the homogeneous term is suitably
substituted with an exponential function, equivalent
to the original one in integral terms.
To fully solve the problem, it is necessary to
determine constants
1
C
and
2
C
. They are found
from initial conditions:
0000
*
2
0
PK
dt
dP
P
t
v
v
(12)
which lead to determine the concentration of
vulcanized polymer within the mixture during the
vulcanization range. The crosslinking density obeys
the following closed form equation:
2
5
2
4
2
35432
22
1
2
012
2
01
2
021
2
2
2
2
01
2
01
1
21
~~
~
~
2/
2
2
1
222
1
22
01
KKKKKKKKK
KPKKPKPKK
KK
K
PK
C
PK
C
eeCeCtP
tPK
tt
v
(13)
Kinetic constants to determine are only three, i.e.
1
K
,
2
K
and
2
~
K
.
The most straightforward method to have a
numerical estimation of kinetic constants is to fit
equation (13) on experimental scorch curve,
normalized scaling the peak value to
0
P
and
translating the initial rotation resistance to zero, as
suggested by Ding and Leonov (1996).
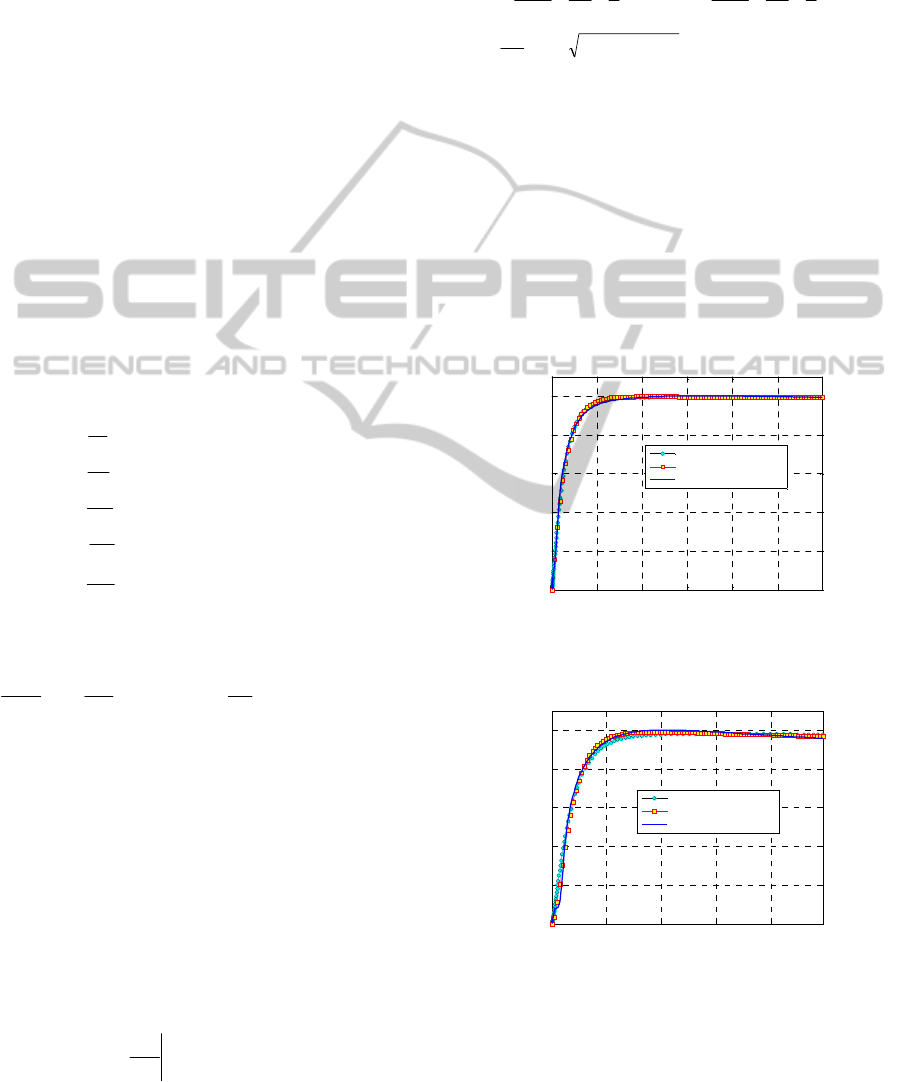
Figure 6: Dutral TER 4049 160°C. Comparison between
experimental data and the numerical models proposed.
Figure 7: Dutral TER 4049 200°C. Comparison between
experimental data and the numerical models proposed.
As a rule, variables
1
K
,
2
K
and
2
~
K
are
estimated through a standard nonlinear least square
routine. Since the problem is rather easy to handle, a
0 20 40 60 80 100
0
0.2
0.4
0.6
0.8
1
Tim e [mi n]
Normalized torque M
t
/M
tmax
Dutral TER 4049 160°C
ODEs system solution
Single DIFF-EQ solution
Experimental
0 2 4 6 8
0
0.2
0.4
0.6
0.8
1
Time [min]
Normalized torque M
t
/M
tmax
Dutral TER 4049 200°C
ODEs system solution
Single DIFF-EQ solution
Experimental
CROSSLINKING BY PEROXIDE AND SULPHUR VULCANIZATION: CHEMICAL MECHANISMS AND
REACTION KINETIC DETERMINATION - A Comprehensive Numerical Model
91

trust-region-reflective algorithm is used. This
algorithm is a subspace trust-region method and is
based on the interior-reflective Newton method.
Each iteration involves the approximate solution of a
linear system using the method of preconditioned
conjugate gradients (PCG).
3.2 Numerical Simulations
To assess model results, some experimental data
available, Milani & Milani (2011b) (cure-meter
curves for a commercial blend called Dutral TER
4049) are considered as reference data. To perform a
numerical optimization of the kinetic model
proposed, experimental cure values are normalized
dividing each point of the curve by the maximum
torque values, so that experimental data are always
within the range 0-1. In Figure 6 and Figure 7, a
comparison between cure curves provided by the
present approach and experimental results is
sketched for Dutral TER 4049, for a temperature
equal to 160°C and 200°C. Data for 180°C are also
available, but are not reported here for the sake of
conciseness.
As it is possible to notice, an almost perfect
agreement between the experimental data and the
numerical procedure proposed is found in both
cases, meaning that the simple second order
differential equation model proposed may represent
a valuable tool for all practitioners interested in a
fast evaluation of the reticulation degree of rubber
compounds vulcanized with accelerated sulphur.
4 CONCLUSIONS
From the results presented in this paper, the
following conclusions can be drawn:
1. Both the GA and the AT approaches are able to
determine optimal input parameters to optimize the
production of medium and high voltage power
cables, as well as of thick 3D items.
2. Numerical simulations have shown how different
mixtures of peroxides may: a) reduce optimal curing
time at almost constant optimized tensile strength or
b) increase optimal tensile strength with an
acceptable increase of curing time. Therefore, the
numerical procedure proposed may represent a
valuable tool for practitioners to obtain high quality
vulcanized items, limiting total curing time required.
3. For sulphur vulcanization, we have proposed a
mathematical kinetic model to predict EPDM
compounds reticulation level, which is based on a
best fitting procedure of experimental cure curves
obtained through rubber process analyzers (RPA
2000) following the ASTM D 5289 method or
ASTM D 2084-81 in a predetermined temperature
range. A simple second order non homogeneous
differential equation model has been derived directly
from the partial reactions occurring in series and
parallel during vulcanization with accelerated
sulphur. The model has demonstrated good
performance when compared to experimental cure-
curves available from a previous experimentation by
the authors.
REFERENCES
ASTM D 2084-81 and ASTM D 5289, Standard Test
Methods for Vulcanized Rubber and Thermoplastic
Elastomers.
Brydson, J. A., 1988. Rubbery Materials and Their
Compounds, Elsevier Science Publishers LTD, Essex.
Ding, R., Leonov, I., 1996. A kinetic model for sulfur
accelerated vulcanization of a natural rubber
compound. Journal of Applied Polymer Science, 61:
45.
Evans, G., Blackledge, J., Yardley, P., 2001. Numerical
methods for partial differential equations. Springer-
Verlag, Berlin, 2nd edition.
Goodyear, C., 1844. US Patent 3633.
Kresja, M. R., Koenig, J. L., 1993. A review of sulphur
cross-linking fundamentals for accelerated and
unaccelerated vulcanization.Rubber Chemistry and
Technology, 66: 376.
Milani, G., Milani, F., 2008. Genetic algorithm for the
optimization of rubber insulated high voltage power
cables production lines. Computers & Chemical
Engineering, 32: 3198-3212.
Milani, G., Milani, F., 2009. Optimization of power cable
production lines for EPM/EPDM elastomers by
Genetic Algorithm with different peroxides. Journal of
Applied Polymer Science, 111(1): 482-507.
Milani, G., Milani, F., 2010b. Optimal vulcanization of
2D-3D EPM/EPDM thick elements through peroxidic
mixtures. Journal of Mathematical Chemistry 47(1),
pp. 229-267.
Milani, G., Milani, F., 2010a. A new simple numerical
model based on experimental scorch curve data fitting
for the interpretation of sulphur vulcanization. Journal
of Mathematical Chemistry, 48: 530–557.
Milani, G., Milani, F., 2011a. A three function numerical
model for the prediction of vulcanization-reversion of
rubber during sulphur curing. Journal of
AppliedPolymer Science, 119(2), pp. 419–437.
Milani, G., Milani, F., 2011b. Simple kinetic model fitting
rheometer data for EPDMacceleratedsulphur. Under
review.
Treloar, L. R. G., 1975. The Physics of Rubber
Elasticity,3d ed., Clarendon Press, Oxford.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
92
