
THE BRAIDED RECONSTRUCTION THEOREMS
Duanliang Liu, Shouchuan Zhang
Department of Mathematics, Hunan University, Changsha, P.R. China
Yange Xu, Guichao Wu
Department of Mathematics, Pingdingshan College, Pingdingshan, P.R. China
Department of Mathematics, Hunan University, Changsha, P.R. China
Keywords:
Braided Hopf algebra, (Co)Quasitriangular, Braided reconstruction theorem.
Abstract:
In this paper, we introduce the method (transmutation) turning an ordinary (co)quasitriangular Hopf algebra
into a braided Hopf algebra, and give the other one which is dual to it.
1 INTRODUCTION
Braided tensor categories become more and more im-
portant. They have been applied in conformal field,
vertex operator algebras, isotopy invariants of links
(see(Huang, 2005; Huang and Kong, 2004; Bakalov
and Kirillov, 2001; Hennings, 1991; Kauffman, 1997;
Radford, 1994)). So studying in braided tensor cat-
egories is interesting, some jobs have been done(see
(Zhang, 2003; Shouchuan and Yange, 2008; Xu and
Zhang)). In this paper, we will turn an ordinary
(co)quasitriangular Hopf algebra into a braided Hopf
algebra, which is due to S. Majid (Majid, 1995). Of
course, our results only hold in symmetric braided
tensor categories, others need be studied furthermore.
Since every braided tensor category is always equiv-
alent to a strict braided tensor category, we can view
every braided tensor as a strict braided tensor and use
braiding diagrams freely.
Some Notations. Let (D , ⊗, I, C) be a braided tensor
category, where I is the identity object and C is the
braiding, with the inverseC
−1
. For f :U → V, g :V →
W, h: I →V, k :U → I, α :U ⊗V → P, α
I
:U ⊗V → I
are morphisms in D , we denote them by:
f =
U
f
V
, gf =
U
f
g
W
, h =
h
V
, k =
U
k
, α =
U V
α
P
, α
I
=
U V
α
I
,
C
U,V
=
U V
V U
, C
−1
U,V
=
V U
U V
,
C
U,V
= C
−1
U,V
=
U V
V U
where U, V, W are in D .
Let C be a tensor category, the braided bialgebra
(H, R,
¯
∆) in C is called quasitrangular bialgebra, if
(H,
¯
∆, ε) is a co-algebra and satisfy:
(QT1):
R
∆
H H H
=
R
R
H H H
(QT2):
R
¯
∆
H H A
=
R
R
H H H
(QT3):
H
R
H H
=
H
¯
∆
R
H H
.
400
Liu D., Zhang S., Xu Y. and Wu G..
THE BRAIDED RECONSTRUCTION THEOREMS.
DOI: 10.5220/0003543904000403
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 400-403
ISBN: 978-989-8425-55-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

(H, R,
¯
∆) is also named that braided quasitrangu-
lar bialgebra in C , with R ∈ Hom
C
(I, H ⊗ H) has
convolution-invertible.
Dually, braided bialgebra (H, r, ¯m) is called
braided co-quasitrangular bialgebra in C , if (H, ¯m, ε)
is an algebra and satisfy:
(CQT1):
H H H
r
=
H H H
r
r
(CQT2):
H H H
¯m
r
=
H H H
r
r
(CQT3):
H H
r
H
=
H H
¯m
r
H
and r ∈ Hom
C
(H ⊗ H, I) has convolution-invertible
too.
2 THE BRAIDED
RECONSTRUCTION
THEOREM I
Let C be a tensor category, D a braided tensor cate-
gory and (F, µ
0
, µ) a tensor functor from C to D with
µ
0
= id
I
. Let Nat(G, T) denote all the natural trans-
formations from functor G to functor T. Assume that
there is an object B of D and a natural transformation
α in Nat(B⊗ F, F). Here (B⊗ F)(X) = B⊗ F(X) for
any object X in D .
Lemma 2.1. ((Zhang)) H be a bialgebra in symmet-
ric braided tensor category, then (i) (H, R) is quasitri-
angular Hopf algebra iff (
H
M , C
R
) is braided tensor
category. (ii) (H, r) is co-quasitriangular Hopf alge-
bra iff (
H
M , C
r
) is braided tensor category.
Theorem 2.2. Let X be a symmetric braided tensor
category, H be a Hopf algebra and (H
1
, R) be a qua-
sitriangular Hopf algebra in X . Let f be a bialgebra
homomorphism from H
1
to H. Then
(i) There exists a bialgebra B(braided Hopf alge-
bra if H has left dual), written as B(H
1
, f, H), liv-
ing in (
H
1
M , C
R
). Here B(H
1
, f, H) = H as algebra,
its counit is ε
H
, and its comultiplication and antipode
are:
B
H H
=
B
R
f
fS
ad
H H
and
B
S
B
B
=
B
R
f
f
ad
S
B
respectively.
(ii) If H is a braided quasitriangular bialgebra,
then B is a braided quasitriangular bialgebra. In par-
ticular, when H = H
1
and f = id
H
, B(H
1
, f, H) is a
braided group, called the braided group analogue of
H and written as H.
Proof (i)Set C =
H
M , D = (
H
1
M , C
R
). Let F
be the functor by pull-back along f. That is, for any
(X, α
X
) ∈
H
M , we obtain an H
1
-module (X, α
′
X
) with
α
′
X
= α
X
( f ⊗ id
X
), written as (X, α
′
X
) = F(X). For
any morphism g ∈ Hom
C
(U, V), define F(g) = g. B
is a left B-module by adjoint action. Let B
L
denote
the left regular B-module. Obviously, α is a natural
transformation from B ⊗ F to F. Now, we show that
θ
V
is injective for any V ∈
H
1
M . If θ
V
(g) = θ
V
(h).It
is straightforward since g and h are H
1
-module homo-
morphisoms from V to B. Similary, we can show that
θ
(2)
V
and θ
(3)
V
are injective.
Obviously, B is a braided bialgebra living in
(
H
1
M , C
R
) determined by braided reconstruction.
THE BRAIDED RECONSTRUCTION THEOREMS
401
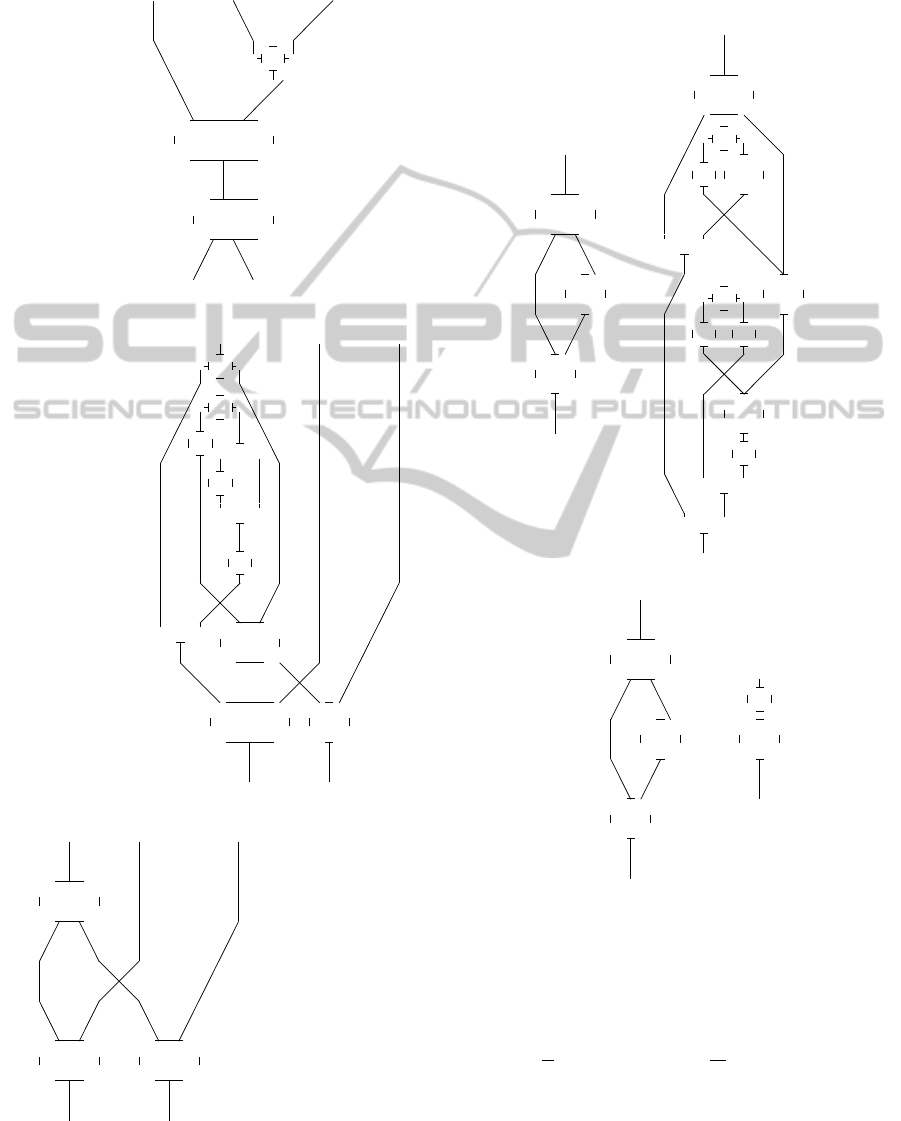
Now we prove that, the comultiplication of B is
the same as stated. That is, we need to show that:
θ
(2)
B
(∆
B
)
X⊗Y
=
B F(X) F(Y)
µ
α
X⊗Y
µ
−1
F(X) F(Y)
(1)
The left side of (1) =
B F(X) F(Y)
∆
H
R
f
S
f
ad
α
X
α
Y
F(X) F(Y)
=
B F(X) F(Y)
∆
H
α
X
α
Y
F(X) F(Y)
= the right side of (1).
If H has left dual, set C = {M ∈
H
M |
Mhas left dual}, it is clear that C is a rigid tensor cate-
gory(every object has a left dual). Thus B is a braided
Hopf algebra.
And
B
∆
B
S
B
m
B
B
=
B
∆
H
R
f
fS
R
ad
f
f
ad
S
B
=
B
∆
H
S
H
m
H
B
=
B
ε
η
H
B
,
which show that the definition of the antipode of B is
reasonable.
If H is a quasitriangular Hopf algebra,
H
M is
braided tensor category by lemma 2.1, then by propo-
sition 1.1 (iii), B is a quasitriangular Hopf algebra.
If H
1
= H, F is identical functor in
H
M , and let
¯
∆ = ∆
B
= ∆, R
B
= η ⊗ η, then H is a braided group.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
402

3 THE BRAIDED
RECONSTRUCTION
THEOREM II
The notation like C , D , (F, µ
0
, µ), Nat(G, T) are same
as stated in section 1. Assume that B is a object of D ,
and φ is natural transformation in Nat(F, B⊗F). Here
(B⊗ F)(X) = B⊗ F(X) for any X ∈ D .
Theorem 3.1. Let X be a symmetric braided tensor
category, H be a Hopf algebra and (H
1
, r) be a coqu-
asitriangular Hopf algebra in X . Let f be a bialgebra
homomorphism from H
1
to H. Then
(i) There exists a bialgebra B(braided Hopf algebra
if H has right dual), written as B(H
1
, f, H), living in
(
H
1
M , C
r
). Here B(H
1
, f, H) = H as coalgebra, its
unit is η
H
, and its multiplication and antipode are:
H H
B
=
H H
cd
f
Sf
r
B
;
B
S
B
B
=
B
S
cd
f
f
r
B
respectively.
(ii) If H is a braided coquasitriangular bialgebra,
then B is a braided coquasitriangular bialgebra. In
particular, when H = H
1
and f = id
H
, B(H
1
, f, H) is
a braided group, called the braided group analogue
of H and written as H.
REFERENCES
Yi-Zhi Huang, Vertex operator algebras, the Verlinde con-
jecture and modular tensor categories, Proc. Nat.
Acad. Sci. 102 (2005) 5352-5356.
Yi-Zhi Huang, Liang Kong, Open-string vertex algebras,
tensor categories and operads, Commun.Math.Phys.
250 (2004) 433-471.
B. Bakalov, A. Kirillov, Lectures on tensor categories and
modular functors, University Lecture Series Vol. 21,
American Mathematical Society, Providence, 2001.
M. A. Hennings, Hopf algebras and regular isotopy invari-
ants for link diagrams, Proc. Cambridge Phil. Soc.
109(1991) 59-77.
L. Kauffman, Invariants of links and 3-manifolds via Hopf
algebras, in Geometry and Physics, Marcel Dekker
Lecture Notes in Pure and Appl. Math. 184 (1997)
471-479.
D. E. Radford, The trace function and Hopf algebras, J. Al-
gebra. 163 (1994), 583-622.
Shouchuan Zhang, Duality theorem and Drinfeld double in
braided tensor categories, Algebra Colloq. 10 (2003)2,
127-134. math.RA/0307255.
Zhang Shouchuan, Xu Yange, The Factorization of Braided
Hopf Algebras, Journal of Mathematical Research
and Exposition, 28(2008)3 489-497.
Yange Xu, Shouchuan Zhang, Duality theorem and Hom
functor in braided tensor categories(to appear), Int. J.
Mod. Math.
S. Majid, Foundations of quantum group theory, Cambridge
University Press, 1995.
Shouchuan Zhang, Braided Hopf Algebras, Hunan Normal
University Press, Changsha, Second edition. Also in
math. RA/0511251.
THE BRAIDED RECONSTRUCTION THEOREMS
403
