
A WIDELY INFINITE PAST PREDICTION PROCEDURE
Jes´us Navarro-Moreno, Rosa M. Fern´andez-Alcal´a, Juan C. Ruiz-Molina and Antonia Oya
Department of Statistics and Operations Research, University of Ja´en, 23071 Ja´en, Spain
Keywords:
Prediction theory, Transfer function models, Widely linear processing.
Abstract:
Using a widely linear (WL) processing, a prediction algorithm has been designed for WL transfer function
models in terms of an infinite number of past observations. This algorithm leads to a suboptimum infinite
past predictor which approximates the optimal predictor based on a finite past information when the size of
the series goes to infinite. Hence, the applicability of our solution lies in those situations where the predictor
based on a finite past is difficult to obtain.
1 INTRODUCTION
Prediction based upon an infinite number of past ob-
servations is a problem of great relevance in statistical
communication theory. Specifically, in those situa-
tions where the predictor based on finite past is diffi-
cult to obtain because of the number of available ob-
servations is extremely large, infinite past prediction
problemsprovidefeasible recursivealgorithmsfor the
computation of a suboptimum estimate which approx-
imates the finite past predictor optimally [see, for ex-
ample, (Brockwell and Davis, 1991)].
In particular, this strategy has been widely used
in transfer function models (Box and Jenkins, 1970;
Brockwell and Davis, 1991). Transfer function mod-
els, also called dynamic regression models, are exten-
sions of familiar linear regression models which in-
clude not only information related to the past of the
time series of interest but also the present and past
values of other time series. Thus, the prediction of
the first time series may be considerably improved by
using information coming from the second.
On the other hand, the widely linear (WL) pro-
cessing has provided a new perspective for solving
several problems concerned with noncircular or im-
proper complex-valued time series. This approach,
based on the information supplied by both the sig-
nal and its conjugate, has shown its efficiency against
the conventional or strictly linear (SL) processing in
many areas of statistical signal processing such as
modeling and estimation, among others [see, e.g.,
(Mandic and Goh, 2009; Navarro-Moreno, 2008;
Navarro-Moreno et al., 2009; Picinbono and Cheva-
lier, 1995; Picinbono and Bondon, 1997)]. Indeed,
in the modeling field, WL systems appear to be more
suitable than SL systems in the representation of this
type of signal. In this framework, the WL finite past
prediction problem for WL ARMA models has been
studied in (Navarro-Moreno, 2008).
This paper tackles the WL infinite past prediction
problem for a more general WL system than the one
considered in (Navarro-Moreno, 2008). Specifically,
the time series of interest is assumed to be modeled
by a WL transfer function system and thus, following
a WL processing, a recursive prediction algorithm is
devised from the infinite past information supplied by
both the input and output of such a model. This al-
gorithm becomes an alternative approach to the WL
finite past prediction problem of this type of system
which, in general, is difficult to address. For this pur-
pose, we first introduce WL transfer function models
in Section 2. Next, the WL infinite past prediction
problem is addressed in Section 3. Finally, an illus-
trative example is developed in Section 4.
2 WL TRANSFER FUNCTION
MODELS
To start with, we introduce some important notations
that will be used throughout the paper.
The real part of a complex number will be denoted
by ℜ{ ·}, the transpose of a vector by (·)
′
, the complex
conjugate by (·)
∗
and the conjugate transpose by (·)
H
.
In general, we will consider the augmented version
X
t
= [X
t
, X
∗
t
]
′
of the complex-valued random process
X
t
.
441
Navarro-Moreno J., M. Fernández-Alcalá R., C. Ruiz-Molina J. and Oya A..
A WIDELY INFINITE PAST PREDICTION PROCEDURE.
DOI: 10.5220/0003544704410444
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 441-444
ISBN: 978-989-8425-74-4
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Moreover, M
2
represents the set of 2×2 complex-
valued matrices
1
A
j
=
a
1j
a
2j
a
∗
2j
a
∗
1j
Now, to attain the WL infinite past prediction
problem, we consider a more general WL model than
those previously suggested in (Picinbono and Bon-
don, 1997; Navarro-Moreno, 2008; Box and Jenkins,
1970). Specifically, let a process Y
t
which is the out-
put of the transfer function model
Y
t
=
∞
∑
j=0
t
1j
X
t−j
+ t
2j
X
∗
t−j
+ N
t
(1)
which satisfies the following characteristics:
• The input process X
t
satisfies the WL ARMA sys-
tem (Navarro-Moreno, 2008)
X
t
=
p
1
∑
j=1
g
1j
X
t−j
+ g
2j
X
∗
t−j
+
q
1
∑
j=0
h
1j
Z
t−j
+ h
2j
Z
∗
t−j
(2)
where Z
t
is a centered doubly white noise with
correlation function E[Z
i
Z
∗
j
] = d
1
δ(i − j) and
complementary function E[Z
i
Z
j
] = d
2
δ
ij
, with
|d
2
| < d
1
and δ
ij
the Kronecker delta function.
• The noise N
t
is supposed to be generated by a WL
system
N
t
=
p
2
∑
j=1
m
1j
N
t−j
+ m
2j
N
∗
t−j
+
q
2
∑
j=0
l
1j
W
t−j
+ l
2j
W
∗
t−j
(3)
with E[W
i
W
∗
j
] = e
1
δ(i− j), E[W
i
W
j
] = e
2
δ(i− j),
|e
2
| < e
1
and the augmented noises Z
t
and W
t
are
uncorrelated.
As it is usual in the prediction process for transfer
function models, the predictor of Y
t
based on a fi-
nite past is, in general, difficult to obtain and the
only simple way to compute the predictor is by us-
ing the infinite past (Box and Jenkins, 1970; Brock-
well and Davis, 1991). Thus, our aim here is to
predict the process Y
n+s
based on the infinite joint
past {[Y
t
, X
t
]
′
, −∞ < t ≤ n} under a WL processing.
Specifically, expressions for computing this WL in-
finite past predictor, denoted by
ˆ
Y
WL
n+s
, as well as its
1
M
2
constitutes a matrix algebra which is closed un-
der addition, multiplication, inversion (when inverses ex-
ist), and multiplication with a real, but not with a complex
scalar.
associated mean square error are provided in the next
section. The proofs and further details about these
results here can be found in (Navarro-Moreno et al.,
2011).
3 WL INFINITE PAST
PREDICTION
First of all, we must note that the WL infinite past pre-
dictor
ˆ
Y
WL
n+s
is the projection of Y
n+s
onto the space
2
H
∞
= sp{[Y
t
, X
t
]
′
, −∞ < t ≤ n}.
Then, introducing the following three types of ma-
trix operators
G
−
p
(B) := I−
p
∑
i=1
G
i
B
i
H
q
(B) :=
q
∑
j=0
H
j
B
j
T(B) :=
∞
∑
k=0
T
k
B
k
with I the identity matrix, B
j
the backward shift oper-
ator (B
j
X
t
= X
t−j
) and G
i
, H
j
, T
k
∈ M
2
, i = 1, . . . , p,
j = 0, 1, . . . , q, k = 0, 1, . . . , equations (1), (2) and (3)
can be rewritten in terms of the augmented processes
Y
t
, X
t
, Z
t
, N
t
and W
t
as
Y
t
= T(B)X
t
+ N
t
G
−
p
1
(B)X
t
= H
q
1
(B)Z
t
M
−
p
2
(B)N
t
= L
q
2
(B)W
t
and hence, it is clear that H
∞
= sp{[Z
t
, W
t
]
′
, −∞ <
t ≤ n}. This fact leads to the following expressions
for the WL infinite past predictor Y
n+s
as well as its
mean square error
Theorem 1. The WL infinite past predictor
ˆ
Y
WL
n+s
of
the process Y
t
given by (1), has the following form
ˆ
Y
WL
n+s
=
∞
∑
j=s
a
1j
Z
n+s−j
+ a
2j
Z
∗
n+s−j
+
∞
∑
j=s
f
1j
W
n+s−j
+ f
2j
W
∗
n+s−j
(4)
where the coefficients a
1j
, a
2j
, f
1j
, f
2j
are obtained
from the equations
∞
∑
j=0
A
j
B
j
= T(B)(G
−
p
1
)
−1
(B)H
q
1
(B)
∞
∑
j=0
F
j
B
j
= (M
−
p
2
)
−1
(B)L
q
2
(B)
(5)
2
sp{[Y
t
, X
t
]
′
, −∞ < t ≤ n} denotes the closed span of
the vectors set {[Y
t
, X
t
]
′
, −∞ < t ≤n}.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
442

with A
j
, F
j
∈ M
2
, j = 0, 1, . . . Also the error of
ˆ
Y
WL
n+s
is
Error(
ˆ
Y
WL
n+s
) = E
h
Y
n+s
−
ˆ
Y
WL
n+s
2
i
=
s−1
∑
j=0
2ℜ{a
1j
d
2
a
∗
2j
}+ a
1j
d
1
a
∗
1j
+ a
2j
d
1
a
∗
2j
+
s−1
∑
j=0
2ℜ{f
1j
e
2
f
∗
2j
}+ f
1j
e
1
f
∗
1j
+ f
2j
e
1
f
∗
2j
(6)
Representation (4) is not convenient from the
computational point of view since it depends on an
infinite number of past observations and thus another
expression is necessary. For this purpose, using oper-
ators of the form (Box and Jenkins, 1970)
T(B) := (V
−
p
3
)
−1
(B)R
q
3
(B)B
b
with V
i
, R
j
∈ M
2
, i = 1, . . . , p
3
and j = 0, 1, . . . , q
3
,
a recursive expression for computing the WL infinite
past predictor Y
n+s
is derived in next theorem
Theorem2. The WL infinite past predictor
ˆ
Y
WL
n+s
of the
process Y
t
given by (1), can be computed as follows:
ˆ
Y
WL
n+s
=
p
3
∑
j=1
v
1j
ˆ
Y
WL
n+s−j
+ v
2j
ˆ
Y
WL
∗
n+s−j
+
q
3
∑
j=0
r
1j
ˆ
X
WL
n+s−b−j
+ r
2j
ˆ
X
WL
∗
n+s−b−j
+
p
4
∑
j=s
c
1j
W
n+s−j
+ c
2j
W
∗
n+s−j
(7)
with
ˆ
Y
WL
j
= Y
j
and
ˆ
X
WL
j
= X
j
, j = 1, . . . , n and where
ˆ
X
WL
j
is the WL predictor of X
j
calculated throughout
the expressions
ˆ
X
WL
n+1
= −
∞
∑
j=1
¯
k
1j
X
n+1−j
+
¯
k
2j
X
∗
n+1−j
ˆ
X
WL
n+2
= −
¯
k
1,1
ˆ
X
WL
n+1
−
¯
k
2,1
ˆ
X
WL
∗
n+1
−
∞
∑
j=2
¯
k
1j
X
n+2−j
+
¯
k
2j
X
∗
n+2−j
.
.
.
(8)
Moreover, for s ≤ p
4
, the coefficients c
1j
, c
2j
are
the elements of C
j
, obtained from the equation
p
4
∑
j=0
C
j
B
j
= V
−
p
3
(B)(M
−
p
2
)
−1
(B)L
q
2
(B)
with C
j
∈ M
2
, j = 0, . . . , p
4
and, for s > p
4
, the last
term in (7) vanishes.
Remark 1. For large n, we can define a WL subop-
timum predictor by truncating (8) at n terms and re-
placing in (7), the predictors
ˆ
X
WL
j
by the approximate
predictors
˜
X
WL
j
given by the expressions
˜
X
WL
n+1
= −
n
∑
j=1
¯
k
1j
X
n+1−j
+
¯
k
2j
X
∗
n+1−j
˜
X
WL
n+2
= −
¯
k
1,1
˜
X
WL
n+1
−
¯
k
2,1
˜
X
WL
∗
n+1
−
n+1
∑
j=2
¯
k
1j
X
n+2−j
+
¯
k
2j
X
∗
n+2−j
.
.
.
˜
X
WL
n+s
= −
n+s−1
∑
j=1
¯
k
1j
˜
X
WL
n+s−j
+
¯
k
2j
˜
X
WL
∗
n+s−j
with
˜
X
WL
j
= X
j
, j = 1, . . . , n.
The performance of the resultant finite past pre-
dictor can be assessed by comparing its error with
the lower bound found in (6).
4 NUMERICAL EXAMPLE
Consider the WL transfer function model
Y
t
= X
t
+ exp{5j}X
∗
t
+ N
t
where j =
√
−1 and X
t
and N
t
are the following WL
MA(1) and MA(2) models respectively
X
t
= Z
t
+ Z
t− 1
N
t
= W
t
+ 0.5W
t− 1
+ 2W
∗
t− 1
+ 3W
∗
t− 2
with E[Z
i
Z
∗
j
] = δ(i − j), E[Z
i
Z
j
] = d
2
δ(i − j),
E[W
i
W
∗
j
] = δ(i− j) and E[W
i
W
j
] = e
2
δ(i− j).
We carry out an analysis of prediction for s = 1, 2
in function of d
2
and e
2
, with d
2
and e
2
varying be-
tween 0 and 0.99. Denote the errors associated with
the WL and with SL predictors for every value d
2
and
e
2
by Error(
ˆ
Y
WL
n+s
(d
2
, e
2
)) and Error(
ˆ
Y
SL
n+s
(d
2
, e
2
)), re-
spectively. From (6) it can be shown that
Error(
ˆ
Y
WL
n+1
(d
2
, e
2
)) = 2ℜ{exp{−5j}d
2
}+ 3
Error(
ˆ
Y
WL
n+2
(d
2
, e
2
)) = 4ℜ{exp{−5j}d
2
}+ 2e
2
+ 9.25
Figures 1 and 2 depict the following error dif-
ferences: Error(
ˆ
Y
SL
n+1
(d
2
, e
2
)) − Error(
ˆ
Y
WL
n+1
(d
2
, e
2
))
and Error(Y
SL
n+2
(d
2
, e
2
))−Error(Y
WL
n+2
(d
2
, e
2
)), respec-
tively. We can observe that the WL predictor has a
slight better performance in the case of one-stage pre-
diction than in the case of two-stage prediction, that
A WIDELY INFINITE PAST PREDICTION PROCEDURE
443
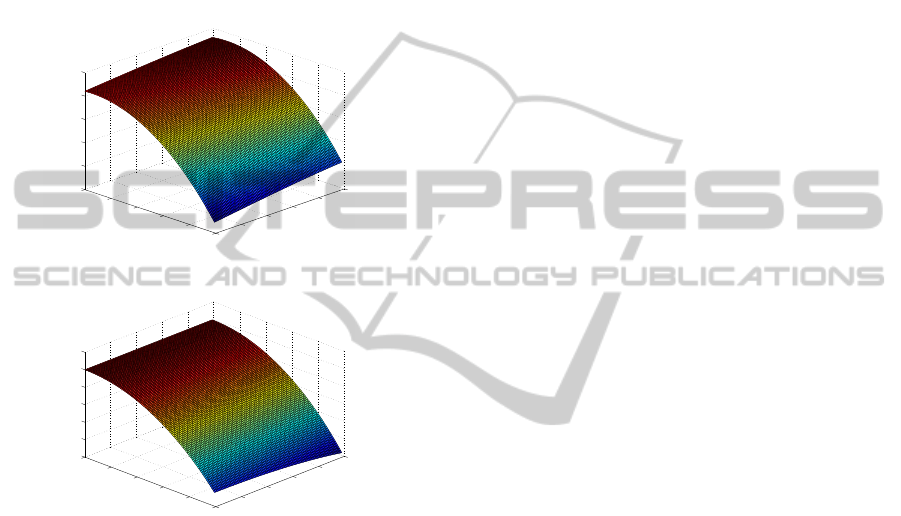
is, the WL one-aheadpredictor attains a greater differ-
ence with respect to the SL one-ahead predictor than
that achieved by the WL two-ahead predictor in rela-
tion to the SL. Moreover, the noise N
t
has a greater
influence on the difference of errors than the noise Z
t
,
i.e., we observe a more significant change in this dif-
ference if a value of d
2
is fixed and we vary e
2
than if
we fix a value of e
2
while d
2
varies. Finally, the ad-
vantages of WL processing are lost when s > 2 since
the WL and the SL predictors coincide.
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
8.6
8.8
9
9.2
9.4
9.6
d
2
e
2
Figure 1: Error(
ˆ
Y
SL
n+1
(d
2
, e
2
)) −Error(
ˆ
Y
WL
n+1
(d
2
, e
2
)).
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
8
8.2
8.4
8.6
8.8
9
9.2
d
2
e
2
Figure 2: Error(
ˆ
Y
SL
n+2
(d
2
, e
2
)) −Error(
ˆ
Y
WL
n+2
(d
2
, e
2
)).
ACKNOWLEDGEMENTS
This work was supported in part by Project
MTM2007-66791 of the Plan Nacional de I+D+I,
Ministerio de Educaci´on y Ciencia, Spain, which is
financed jointly by the FEDER.
REFERENCES
Box, G. and Jenkins, G. (1970). Time Series Analysis: Fore-
casting and Control. Holden-Day, San Francisco.
Brockwell, P. and Davis, R. (1991). Time Series: Theory
and Methods. Springer-Verlag, New York, 2nd edi-
tion.
Mandic, D. P. and Goh, V. S. L. (2009). Complex Valued
Nonlinear Adaptative Filters. Noncircularity, Widely
Linear and Neural Models. Wiley.
Navarro-Moreno, J. (2008). ARMA Prediction of Widely
Linear Systems by Using the Innovations Algorithm.
IEEE, Trans. Signal Processing, 56(7):3061–3068.
Navarro-Moreno, J., Moreno-Kayser, J., Fern´andez-Alcal´a,
R. M., and Ruiz-Molina, J. C. (2009). Widely Linear
Estimation Algorithms for Second-Order Stationary
Signals. IEEE, Trans. Signal Processing, 51(1):306–
312.
Navarro-Moreno, J., Moreno-Kayser, J., Fern´andez-Alcal´a,
R. M., and Ruiz-Molina, J. C. (2011). Widely Linear
Prediction for Transfer Function Models Based on the
Infinite Past. Computational Statistics & Data Analy-
sis. In press.
Picinbono, B. and Bondon, P. (1997). Second-Order Statis-
tics of Complex Signals. IEEE, Trans. Signal Process-
ing, 45(2):411–420.
Picinbono, B. and Chevalier, P. (1995). Widely Linear Esti-
mation with Complex Data. IEEE, Trans. Signal Pro-
cessing, 43(8):2030–2033.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
444
