
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON
CALCULATING THE WEIGHTS OF ECONOMIC MODEL
EVALUATION
Dai Wang, Dan Chang, Na Luo and Jingyi Xu
School of Economics and Management, Beijing Jiaotong University, No.3 Shangyuancun, Beijing, China
Keywords: Weight, Evaluation system, AHP, Adjust.
Abstract: With the combination of teaching resources and IT technology being more and more close, it has attracted
more attention on the issue of how to manage the quality of online teaching resources. This thesis has
constructed an evaluation system for the model library of the Economic Model Resource Platform, and
adjusted the weighted scales and the corresponding calculations based on both of the theory of the Analytic
Hierarchy Process (AHP to be brief) and the characteristics of the Economic Model Resource Platform
during the process of determining the weights of the evaluation system in order to make the final weights
more suitable for practical applications. This study helps achieve the purposes of monitoring the quality of
the economic models and promoting the optimization of the models. On the other hand, the calculation
method of determining the weights has provided a reference for the application of AHP.
1 INTRODUCTION
With the rapid development of information
technology, network technology gradually
penetrated into the educational applications.
However, with the rapid increase of the amount of
teaching resources on the Internet, how to effectively
improve the quality of teaching resources has gotten
more and more concentration. The foundation of this
thesis is the Economic Model Resource Platform.
This platform which works as a library of the
economic models based on the internet technology
contains 170 models up to now. And the platform is
an important teaching resource with the goals of
training the scientific and engineering thoughts of
the economics and management students and
training them to be the compound and creative
talents. With the increasing number of the models on
the platform, the quality of the models varies greatly,
and needs improving continuously. Therefore, the
management of the models on the platform is
particularly important.
Analytic Hierarchy Process (AHP to be brief) has
the characters of clear, simply, and with strong
systematicness (XIANG Qing, 1997). In recent
years, this method has been widely applied to
analyze and evaluate in many territories such as
social science, economy, education and others. The
examples of the applications come as the
constructing of the analysis method of meandering
river underground reservoir (Yue Dali et al., 2010),
the constructing of the evaluation system of the
emergency logistics plan(MA Li, 2010) , the
constructing of the quality evaluation system in the
hospital work (ZENG Wenting et al., 2010),
analyzing the leading industries in direct foreign
investments (Zhao Fu-hou, 2010), etc.
This thesis is based on AHP. The first step is to
construct the index system of model library
evaluation system, and the second step is to
determine the weights. In the process of the second
step, there is a combination of the theory of AHP
and the characteristics of the application of the
evaluation system. The method of constructing the
judgment matrixes has been adjusted, making it
more suitable with the actual situation. And it proves
to be correct by the validation afterwards.
2 CONSTRUCT THE INDEX
SYSTEM OF ECONOMIC
MODELS
This thesis uses the AHP method to construct the
index system of the economic model evaluation
108
Wang D., Chang D., Luo N. and Xu J..
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON CALCULATING THE WEIGHTS OF ECONOMIC MODEL EVALUATION.
DOI: 10.5220/0003549201080116
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 108-116
ISBN: 978-989-8425-55-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

system (Rong RUAN et al., 2011). Based on the
basic principles of AHP, the index system is divided
into three levels, namely, the target layer, rule layer
and project layer. By consulting criteria of teaching
resources and combining the features of the
economic models, the target layer is divided into
content, technical, effectiveness and application.
Those are the first-level indexes. Then get the target
level indexes in the same way. After this, there are
11 indexes of the criterion level and 24 indexes in
the program level finally.
The index system is shown in Table 6.
3 DETERMINE THE INITIAL
WEIGHTS USING AHP
3.1 Theory and Characteristics of AHP
AHP is proposed by the U.S. operations researcher
T.L Saaty (1980), which is a multi-objective
decision analysis method combined with qualitative
and quantitative analysis. It suits for the problem that
has complex structure and many decision criteria
that are difficult to quantify. The basic idea of AHP
is that the system is decomposed into different
elements according to the nature, decision-making or
evaluation of goals of the object. Then different
elements are arranged from high to low by the
linkages between elements.
AHP is not only a simple method for making
quantitative analysis by non-quantitative systems in
engineering event, but also an effective method to
make subjective judgments on the objective
description.
3.2 The Implementation Steps of AHP
The general process of AHP is, shown in Figure 1.
Analysis
Establish
Hierarchy Model
Construct
Judgment Matrix
Consistency
Test
One Order
Analysis
Sort of the
Total(All
Weights)
Value of
Comprehensive
Evaluation
Decision
Analysis
Conclusion
Ye
s
Yes
No
No
Figure 1: The general process of AHP.
1. Analyze the research questions.
2. Establish the hierarchy models based on the
results of the research questions.
3. Construct the judgment matrix.
4. Conduct consistency test, if the test failed, re-
analyze the problem or construct a new judgment
matrix, else make the single-pass order analysis.
5. Make the total sequencing analysis of all
weights.
6. Test the value of comprehensive evaluation, if
the decision can be accepted, draw conclusions, or
re-test the consistency.
3.3 Application of AHP to Get the
Weights of the Economic Model
Evaluation System
3.3.1 Construct Variables
The economic model evaluation system is divided
into three levels based on the target layer, rule layer
and project layer. Level one indexes include content,
technical, effectiveness and application; the
secondary indexes include integrity, accuracy and
ease of understanding and so on. Indexes have been
shown in Table 6.
Level one indexes will be set respectively
as
1
A
、
2
A
、
3
A
、
4
A
. The secondary indexes
corresponding to level one indexes will be set
respectively as
1m
B
、
2n
B
、
3k
B
(
m
、
n
、
k are natural
numbers
),
so do the third level indexes.
Assume that the weights of the level one
indicators as
1
、
2
、
3
、
4
, and then:
4
1
01 (1,2,3)
1
i
i
i
i
(1)
(2)
Assume that the weights for the secondary indicators
are
ij
( 1, 2,3; 1, 2,..., max( , , ))ij mnk
, and then:
max( , , )
1
max( , , )
3
11
0 1 ( 1,2,3)
1
1
ij
mnk
ij
j
mnk
iij
ij
i
(3)
(4)
(5)
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON CALCULATING THE WEIGHTS OF ECONOMIC
MODEL EVALUATION
109

3.3.2 Determine the Weights of Evaluation
Indexes
(1) Construct judgment matrixes. On the same level,
the result of pair wise comparison can be generally
described by using "important", "slightly important",
"relatively important" and "very important". In AHP,
using
(, )
f
xy
to express whether factors
x
is more
important than factor
y . If
(, ) 1fxy
, it indicates that
x
is more important than y . If
(, ) 1fxy
, it indicates
that
x
is less important than y . Only
when
(, ) 1fxy
, it indicates that
x
and y are
equally important. And it is commonly agreed
that
1
(, )
(,)
fxy
f
yx
.
Numbers 1 to 9 are used to indicate the level of
importance of the indexes. The meanings of the
scales are in Table 1.
Table 1: The meaning of each scale in AHP.
Scale f(x,y) Definition Instructions
1 Equally important i is equally important with j
3
Somewhat
important
i is somewhat more
important than j
5
Relatively
important
i is relatively more
important than j
7 Very important i is more important than j
9
Absolutely
important
i is absolutely more
important than j
2 4 6 8 Between Between the two states
(2) Expert opinion to construct the Matrix method.
In the scoring process, the experts determine the
relative importance ratio of the indicators in the
same level based on their experience. The form of
collecting the data is questionnaire.
According to the evaluation system, we invited 55
experts to rate indexes in order to create a judgment
matrix by questionnaires. The experts are from three
research areas namely Department of Economics,
Department of Logistics and Department of
Information System. After the research, 50
questionnaires were recovered, and the recovery was
90.9%. Because each expert has a certain
understanding of bias and errors, we removed some
radical elements and do descriptive statistics when
using the original data. At last, we received 13
comparison matrixes.
Take the secondary indicators ‘integrity’ for
example. Its third-level indexes’ judgment matrix is
in Table 2.
(3) Calculating the weights and the maximum
eigenvalue of the third-level indexes of ‘integrity’.
Determine the matrix data (Row 2-5, Table 2) in
accordance with the instructions given afterwards.
The following is the calculation of the maximum
eigenvalue of the indexes; the results are in Table 3.
Calculation descriptions:
i
M
:
1/n
n
iij
j
Mb
(6)
Table 2: Judgment matrix of the level 3 indexes of ‘Integrality’.
Integrality Theoretical
source
Assumptions Theory to explain Analysis
Theoretical source 1 2 2 1
Assumptions 1/2 1 2 2
Theory to explain 1/2 1/2 1 1
Analysis 1 1/2 1 1
Table 3: Calculate the index weights and the maximum eigenvalue of the third-level indexes of ‘integrity’.
Scales A B C D Mi Wi (AW)i The largest eigenvalue Weights
A
1.00 2.00 2.00 1.00 1.414214 0.340657 2.043945 0.69628508 0.505198
B
0.50 1.00 2.00 2.00 1.189207 0.286458 1.575517 0.45131891 0.32746
C
0.50 0.50 1.00 1.00 0.707107 0.170329 0.510986 0.08703563 0.06315
D
1.00 0.50 1.00 1.00 0.840896 0.202556 0.708947 0.14360147 0.104192
Total
4.151424 1 1.3782411
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
110

In this case n = 4.
i
W
:
/
n
ii i
i
WM M
(7)
In this case n = 4.
A is comprehensive judgment matrix. Each
number in the number i line in A multiplied by each
number of the corresponding values in the
i
W
column, and the summation of all products is
()
i
A
W
.
The calculation of the maximum eigenvalue:
max
/
i
i
AW n W
(8)
In this case, the maximum eigenvalue is equal to
1.3782411.
(4) Consistency Test. Because the matrix structure
made by the experts do not necessarily meets the
matrix consistency. Judge the matrix consistency
test in order to limit this kind of error. Take the
largest eigenvalue and n's relative error as the
consistency indicator of matrix. Denoted by:
max
1
n
CI
n
(9)
( n equals to the order of matrix, also the number of
indexes in matrix.)
If
2n
,the matrix is always exactly the same, it
means
0CI
。
And when
2n
,the ratio of the
matrix's consistency index and the average random
consistency index is random consistency ratio which
is denoted as
CR
.
If
R<0.1C
, the judgment matrix has satisfactory
consistency and the calculated feature vector is
reliable. Otherwise the matrix the experts
constructed has larger error and is out of range. The
matrix needs to be re-adjusted until it gets the
satisfactory consistency.
After calculation, all comparison matrixes are
consistent, and the results are credible.
(5) Calculation of the total weight. The index system
is composed of the first-level indicators and
secondary indicators. Each first-level indicator
contains numbers of secondary-level indexes. As
described above, we calculate four first-level
indicators' weights, and analyze the consistency of
its matrix. And it is the same to the secondary-level
indexes.
Supposing that the indicator
i 's weight is equal
to
i
a ,its j secondary-level indicator's relative
weight is
j
b .Then this secondary-level indicator's
total weight is
ij
ab
.
In order to verify whether the total weight also
has the satisfaction of consistency, we need to
calculate the total random consistency index, the
indicator is calculated as:
1
1
n
ii
i
n
ii
i
aCI
CR
aRI
(10)
While:
i
a : the number i first-level indicator's weight.
i
CI : the number i first-level indicator's
consistency index value.
i
RI
:
the number i first-level indicator's average
random consistency index values.
The final overall consistency test result is
0.028312 which is far less than 0.1.So it is consistent
with consistency. Evaluation indexes’ weights are in
Table 6, the unadjusted weights.
3.4 Existing Problems in Weights
According to the analysis of the system above, the
following questions are found:
1) There are nine scales 1 to 9 which bring heavy
interference to define the actual level of importance.
According to the statistics, in the valid
questionnaires, 89.93 percent of the scores are
between 1 and 4, and this is not accord with the
actual. And a few high points such as score nine or
eight will cause big effect to the result of the data.
The reason lies in that nine scales range too wide,
and in the economic model evaluation system, the
differences of importance between indexes of the
same layer do not need so big a range. At the same
time, because the differences between the graders
own subjective thoughts, the specific meanings of 1
to 9 are difficult to be defined.
2) Traditional AHP method is applicable to the
systems with fewer indexes, and when they are used
to the economic model evaluation system, the big
workload will make raters be confused with the
concepts of indexes gradually.
3) Due to current mindset, in 90.1% of the
recovered questionnaires, the top right corner data of
judgment matrix are greater than 1. When some
experts do the rating, they default that the front
index is more important than the afterward indexes.
This kind of mindset leads to an obvious weight
stressed phenomenon in the same layer indexes,
namely the index Content’s weight is greater than
80%, which causes the weight of index Application
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON CALCULATING THE WEIGHTS OF ECONOMIC
MODEL EVALUATION
111

can be ignored, or even the indexes of the secondary
layer and the third layer. The phenomenon does not
match the facts.
4 ADJUST THE WEIGHTS OF
THE EVALUATION SYSTEM
4.1 Adjustments
It has shown that the direct application of AHP does
not match the evaluation system exactly based on
the analysis of the evaluation system above. Because
of this, it is needed to adjust the ways of calculating
the weights based on the characteristics and the
actual applications of the Economic Model Resource
Platform and re-calculate them.
The specific adjustments of the application of
AHP are as follows.
1) Narrow the scope of the scales to three numbers.
Narrowing the scope of the scales is more suitable
for this study compared to the initial nine numbers.
2) Set the scales to -1, 0 and 1(YE Jun, WANG Lei,
2010). -1 is introduced into the process in order to
express the degree of the importance of the indexes
and reduce the fatigue caused by the large amount of
work.
The meaning of each scale is shown in Table 4.
Table 4: The meaning of each adjusted scale.
Scale f(x,y) Definition Interpretation
-1
To be less
important
i is less important
than j
0
To be equally
important
i is equally
important with j
1
To be more
important
i is more important
than j
3) Using the adjusted questionnaires to obtain new
data from the same respondents.
4.2 Calculating Weights
(1) Structure the Judgment Matrixes. A judgment
matrix is based on the relative importance of each
index, denoted by C. Still take the level three
indexes of the secondary index ‘Integrality’ for
example. The experts assess the relative importance
of the indexes as ‘Theory to explain’ >
‘Assumptions’ = ‘Theoretical source’ > ‘Analysis’.
And the initial judgment matrix is shown in Table 5.
Thereupon,
00 1 1
00 1 1
11 00
11 0 0
C
(11)
(2) Calculate the optimal transfer matrix. Optimal
transfer matrix is set to be O. According to
1
1
()
n
ij ik kj
k
Occ
n
(12)
Get the optimal matrix as follows:
0 0.50 0.50 0
0.50 0 1.00 0.50
0.50 1.00 0 0.50
0 0.50 0.50 0
O
(13)
(3) Get the consistent matrix. Set the consistent
matrix as K. According to
exp( )
ij ij
ko to get the
consistent matrix as follows:
1.00 1.65 0.61 1.00
0.61 1.00 0.37 0.61
1.65 2.72 1.00 1.65
1.00 1.65 0.61 1.00
K
(14)
(4) Get the weights. Make use of the eigenvector to
get the weights. Set the weight matrix as
T
P
. Then
4
4
1
44
11
ij
j
i
Ti
ii
ii
o
p
p
pp
(15)
Table 5: Adjusted judgment matrix of the level 3 indexes
of ‘Integrality’.
Integrality
Theoretic
al source
Assumptions
Theory to
explain
Analysis
Theoretical
source
0 0 -1 1
Assumptions 0 0 -1 -1
Theory to
explain
1 1 0 0
Analysis -1 1 0 0
And the weight matrix is
0.235 0.143 0.387 0.235
T
P
(16)
(5) Complete the calculation of the weights in the
evaluation system. Complete the calculation of the
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
112
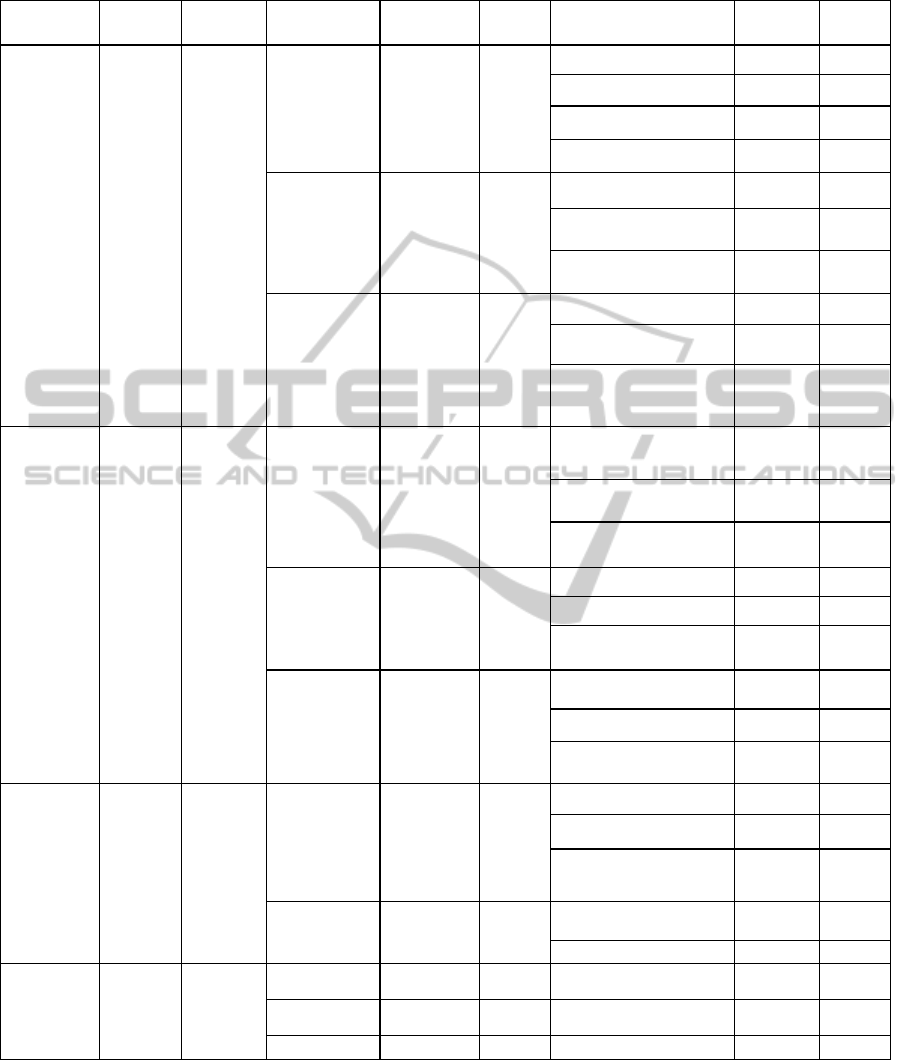
Table 6: Economical model evaluation system and the weights.
A Target layer
Unadjusted
weights
Adjusted
weights
B Rule layer
Unadjusted
weights
Adjusted
weights
C Project layer
Unadjusted
weights
Adjusted
weights
1 Content 0.870 0.276
11 Integrity 0.503 0.124
111 Theoretical source 0.234 0.029
112 Assumptions 0.244 0.017
113 Theory to explain 0.009 0.048
114 Analysis 0.016 0.047
12 Accuracy 0.238 0.089
121 Interpretation accuracy 0.073 0.038
122 The accuracy of
understanding
0.033 0.018
123 Whether to seize the
essence
0.132 0.027
13 Understand-
ability
0.125 0.063
131 Example 0.046 0.018
132 Analogy to explain 0.075 0.009
133 Whether has
interpretation of the
academic term
0.004 0.036
2 Technical 0.080 0.455
21 Operability 0.077 0.256
211 Whether the output of
experimental operation
0.068 0.148
212 Whether the result is
that the process
0.005 0.053
213 Whether has input data
validation
0.004 0.053
22 Friendly
interface
0.002 0.067
221 Tips range of input data 0.002 0.028
222 Sample data 0 0.016
223 The reasonable of the
control
0 0.022
23 Experiment to
explain
0.002 0.131
231 Experiment description 0.002 0.041
232 Interpretation of results 0 0.057
233 Whether is the steps to
explain logical
0 0.030
3 Effectiveness 0.030 0.102
31 Intuitive 0.025 0.027
311 Text 0 0.015
312 Graphic description 0.016 0.008
313 Other visual
presentation methods
0.008 0.004
32 Data Validation 0.075 0.075
321 The length of time to
get result
0 0.054
322 Error rate 0.001 0.018
4 Application 0.030 0.167
41 Case relevance 0.025 0.096 0.025 0.096
42 Case Study 0.001 0.035 0.001 0.035
43 Questions 0 0.035 0 0.035
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON CALCULATING THE WEIGHTS OF ECONOMIC
MODEL EVALUATION
113

entire weights in the evaluation system according to
the methods above. Set the weight of index i as
i
a ,
its secondary index j’s weight as
j
b , and the final
weight of the secondary weight is
ij
ab
.
4.3 The Evaluation System and the
Weights after the Adjustments
According to the methods above, the economical
model evaluation system and the weights are in the
table 6, the adjusted weights.
5 VALIDATION OF THE
EVALUATION INDEXES
5.1 The Basis of the Validation
To verify that the adjusted index’s weights are more
suitable for the economic model evaluation system,
it is needed to test the two sets of weights.
According to the experience of statistics, when
the size of the sample is not less than 30,it is large
sample, and the samples’ average can eliminate
personal biases and errors. In this case, 60 users of
the Economic Model Resource Platform were
selected for the investigation. And they were
randomly divided into group A and group B, 30
people in each group to make the results of the
validation more general and reliable (E.L.Lehman,
2010).
5.2 The Process of the Validation
1) Sampling. Randomly select 20 models from the
170 models in the model library of the Economic
Model Resource Platform, number them 1-20.
2) Select the respondents. Select 60 users of the
Economic Model Resource Platform randomly and
divided them into group A and group B, according
to the methods above.
3) Rating. Let the users of group A rate the models
0-20 according to the practical usage of the models
with 10 being the highest and 0 being the lowest. In
this case, it has been the rules that the scores of 8-10
are level A, 5-8 are level B, and the rest are level C.
4) Scoring. Request the users of group B score the
indexes of the 20 models.
5) Data analysis.
Firstly, the data of Group A were statistically
analyzed. Work out the average score of each model
and rate the models in the method above.
Secondly, put the scores of each index from
group B into the two sets of the index systems to get
two total scores for each model. And take the
average scores of all the raters as the final scores of
the models using two evaluation systems.
Finally, compare the three sets of data, as shown
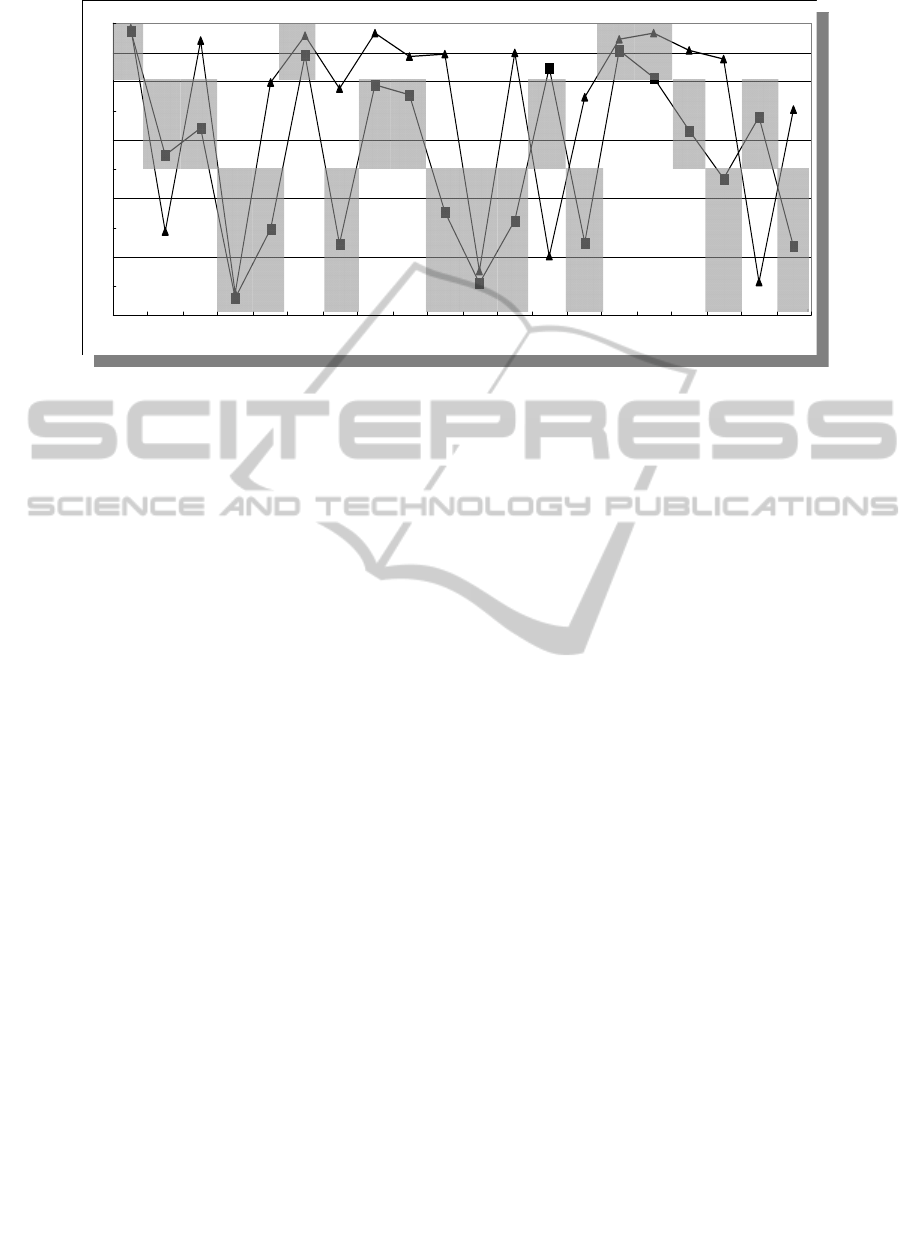
in Table 7.
Notes:
Horizontal axis: Model Numbers.
Vertical axis: Scores.
Grey areas: Levels from Group A.
Triangle marks: Model scores rated by Group B
using the evaluation system unadjusted.
Quadrate markers: Model scores rated by Group B
using the evaluation system after adjusted.
Table 7: The results of the validation.
Model Number 1 2 3 4 5 6 7 8 9 10
Rating by Group A
A B B C C A C B B C
Scoring by Group B(unadjusted)
9.82 2.85 9.43 0.78 7.99 9.58 7.78 9.65 8.87 8.96
Scoring by Group B(adjusted)
9.76 5.48 6.42 0.61 2.97 8.90 2.44 7.87 7.54 3.54
Model Number 11 12 13 14 15 16 17 18 19 20
Rating by Group A
C C B C A A B C B C
Scoring by Group B(unadjusted)
1.54 8.99 2.01 7.45 9.46 9.67 9.06 8.79 1.13 7.06
Scoring by Group B(adjusted)
1.08 3.25 8.50 2.48 9.08 8.16 6.35 4.70 6.78 2.35
The results of the matching are shown in Figure 2.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
114
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Figure 2: The matching Results of the Validation.
5.3 Analysis of the Validation
As is shown above, the number of matched models
between the rating from group A and the scores
gotten by the evaluation system unadjusted is 6
(respectively, model 1, model 4, model 6, model 11,
model 15 and model 16 ), 30% of the total number
of the samples. According to the data, the scores
from the unadjusted evaluation system are extreme,
and most of them are between 7-10 points. Observe
the weight of each index, it can be find that
“Theoretical source”, “Assumptions”,”
Interpretation accuracy ”,“Whether to seize the
essence ”,“Whether the output of experimental
operation” and “Analogy to explain” occupy the
larger share, weighing 82.6% in the whole
evaluation. So they have too much excessive traction
to the final score, resulting in relatively extreme
scores of models.
However, the number of matched models
between the rating from group A and the scores
made by the evaluation system adjusted is 19, 95%
of the total number of the samples. Therefore, the
weights made by the adjusted evaluation system are
more applicable and objective, mainly embodied in
the following three aspects.
Firstly, they solve the unsuitable problem of the
weights made by the unadjusted evaluation system.
Reduce the scales to - 1, 0 and 1 can indicate the
level of importance among indexes more clearly.
Meanwhile, the reduction of the number of scales
eases the workload of respondents and alleviates the
scoring fatigue, thus enhancing the effectiveness of
the initial matrixes. In addition, adjusting scales
solutes the difficulty of discriminating the large
amount of scales.
Secondly, accord with the actual importance of
the indexes. By the weights of the final indexes,
"Experimental operation is output or not" occupies
the largest share, as 14.8%. Followed is "Case
correlation" which occupies as 9.6%. The Economic
Model Resource Platform takes IT as the core, and
focuses on the applications of the models, so the
maneuverability and correlation of the cases indeed
weigh a larger proportion in evaluating the quality of
the models. And the weights of other indexes are
also accord with the actual situation.
Thirdly, be helpful with practical applications.
This economic model evaluation system can show
clearly the total scores of the models and typically
each score of the indexes. It not only evaluates the
models, but also indicates the low grade models’
weak more intuitively, which helps build a clear
target for the administrator to improve the quality of
the models.
6 CONCLUSIONS
There are numerals ways to get the weights of
indexes in an evaluation system. And this thesis gets
the weights by adjusting the process of AHP based
on the theory of AHP and the characteristics of the
Economic Model Resource Platform. This method
not only makes the meaning of the scales more
directly which results in reducing the workload of
scoring and relieving the fatigue of scoring, but also
gets a result more suitable to the practical
applications. The method in this thesis can be used
not only on the Economic Model Resource Platform,
but also provides some references to other similar
studies.
APPLICATION OF ANALYTIC HIERARCHY PROCESS ON CALCULATING THE WEIGHTS OF ECONOMIC
MODEL EVALUATION
115

However, although the way of getting the
weights is adjusted, it is unavoidable that the data
from the experts are some kind of subjective.
Therefore, it is important to choose the proper
experts, both from the experts of the corresponding
subjects and the users of the Economic Model
Resource Platform in order to make the weights of
the indexes more reasonable and practicable. The
users of the Economic Model Resource Platform can
rate the models according to this evaluation, and
when the number of the raters is large enough, we
can get the evaluation of the models.
REFERENCES
Emshoff, J. R.; Saaty, T. L.(1980). Application of the
Analytic Hierarchy Process to Long Range Planning
Processes. European Journal of Operational
Research
, 10(2),131-143.
Hambali, A., & Sapuan, S. M., & Ismail, N. & Nukman,
Y. (2010). Material election of polymeric composite
automotive bumper beam using analytical hierarchy
process. Journal of Central South University of
Technology
, 17 (2), 244-256.
Lehman, E. L. (2010). Elements of Large-Sample Theory.
In: Springer New York, New York.
Li, M. (2010). Based on rough sets and AHP evaluation of
emergency logistics plan. China Logistics and
Purchasing
, 15, 66-67.
Ruan R., & Zhang Z. J., & Meng J. J., & Liu Z. C. (2011).
The construction of economic model evaluation
system. In:
R. T. Zhang, ed. 13
th
International
Conference on Enterprise Information Systems,
Beijing
8-11 June 2011.
Xiang, Q. (1997). "Social Evaluation of Projects"
Review.
Dialectics of Nature
, 13, 24-26.
Ye, J. & Wang, L. (2010). Research on comprehensive
evaluation method based on rough set and AHP.
Computer Applications
,
7, 2486-2488.
Yue, D. L. & Wang J. & Wang Y. Z. & Wu S. H. & Liu J.
M. & Shu Q. L. (2010). Hierarchy analysis in
paleochannel reservoir architecture
:
A case study of
meandering river reservoir of Guantao Formation.
Gudao Oilfield. Geological Sciences, 3, 832-843.
Zhao, F. H. (2010). The Leading Industry Analysis in the
Foreign Direct Investment Industries by Using
Analytic Hierarchy Process.
Industrial Engineering,
13, 91-95.
Zeng, W. T. & Shi L. & Zhao W. L. (2010). The
application of AHP in the five top-three hospitals in
Chongqing City. China Health Statistics, 4, 406-408.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
116
