ACCUMULATING EVIDENCE BASED ON ESTIMATION
THEORY AND HUMAN PSYCHOLOGY
Michael E. Farmer
University of Michigan-Flint, 302 East Kearsley St., Flint, MI, U.S.A.
Keywords: Sensor fusion, Dempster-shafer, Kalman filtering, Belief updating.
Abstract: The traditional D-S conditioning is based on a collection of ‘experts’ inputting their evidence and
accumulating the beliefs. Researchers have often adopted this same mechanism for integrating evidence
from single sources of evidence over time, such as seen in sensor networks. One issue with this approach is
that the order of inputs does not matter. While this is sensible for a collection of experts we propose that it
is not suitable for a single input providing streams of evidence. Likewise research in psychology show
order of integration of evidence does matter, and depending on the application humans have a preference for
recency or primacy. Estimation theory provides frameworks for analyzing data over time, and recently
some researchers have proposed integrating evidence in an estimation-inspired manner. In light of this we
propose a Kalman-filter based approach for integrating single sensor evidence over time where the evidence
conflict plays the role of system noise in adapting the filter gain.
1 INTRODUCTION
There has been significant research in the artificial
intelligence (AI) community with respect to
evidential reasoning and updating beliefs, with the
most common approaches being Bayesian and
Dempster-Shafer. Likewise the field of cognitive
psychology has also been heavily involved in
research in belief updating. There are three key
areas where the existing AI research in evidential
reasoning has differed significantly from the
findings in human cognition, (i) order effects, (ii)
evidence impact reduction in long evidence streams,
and (iii) evidence evaluation versus estimation.
As sensor networks become more prevalent, it is
time to relook at the mechanisms of evidence
accumulation over time to support belief revision
and updating. In sensor networks inputs from
multiple sensors over time are integrated resulting in
both a lateral integration (sensor fusion across
sensors) as well as a longitudinal integration (data
integration over time for each sensor). This spatial-
temporal combining of evidence leads to issues
which have not been fully addressed to date and
relate back to the three issues relating to human
evidential reasoning.
The first issue, namely that of order
independence, is one of the key tenets of the more
common theories, and it is also a critical foundation
of the AGM framework of logic and Dempster
Shafer. Approaches such as Jeffrey’s conditioning
have been shown to have order dependence but it is
an accident of the mathematics and not a conscious
goal of the algorithm (Garber, 1980). This order
independence is not however found to exist in
human reasoning, and there are definite situations
when order-effects are demonstrated in humans
(Hogarth and Einhorn, 1992). as well as being
desirable in sensor networks.
The second issue is that of how to integrate
evidence over long streams of data. In human
cognition ‘as information accumulates, beliefs are
expected to become less sensitive to the impact of
new information because this represents an
increasingly small proportion of evidence already
processed” (Hogarth and Einhorn, 1992). This
contrasts sharply with the common approaches in AI
of Bayes and Dempster-Shafer which weight the
entire history equally with the most recent input.
The third issue related to human cognition is
based on what cognitive researchers call. In human
evidential reasoning there are two approaches,
evaluation and estimation. Evaluation is a process
in which the reasoning tasks tend to be formulated
into a true-false framework. Estimation tasks,
however, are additive in nature and assess ‘how
376
E. Farmer M..
ACCUMULATING EVIDENCE BASED ON ESTIMATION THEORY AND HUMAN PSYCHOLOGY.
DOI: 10.5220/0003569003760381
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 376-381
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

much evidence is to be allocated to a belief’
encoding (Hogarth and Einhorn, 1992). Cognitive
researchers have found that ‘estimation may be
more frequently used than evaluation’, whereas
artificial reasoning systems tend to adopt evaluative
approaches. In this paper we propose a framework
for evidence accumulation from a single sensor over
time devised from first-principles of Kalman
filtering that resolves these differences between
human subject behavior and artificial reasoning
systems.
2 BELIEF REVISION IN HUMAN
PSYCHOLOGY STUDIES
There is considerable research showing the
importance of order in human reasoning. Hogart
and Einhorn (Hogarth and Einhorn, 1992). suggest
that the recency effect is more important when
messages are inconsistent. This result was also
verified by Wang et al. for an interesting Combat
Information Center application (Wang et al., 1999).
Baratgin and Politzer recently address the issue of
updating (dynamic environment) in human decision
making and confirm by reviewing numerous studies
that “a message has greater contextual effects when
it is learnt in the last position” (Baratgin and
Politzer, 2007).
Likewise the repetition of evidence in human
reasoning has also been shown to be important
where repeated repetition of a message changes the
opinions of the test subjects (Baratgin and Politzer,
2007). Hogarth and Einhorn modeled human
behavior through anchoring and adjustment defined
by (Hogarth and Einhorn, 1992):
(
)
[]
(
)
RxsRxsSSS
kkkkk
≤−+=
−−
for
11
α
,
(1)
and
(
)
(
)
[]
(
)
RxsRxsSSS
kkkkk
>
−
−+=
−−
for 1
11
β
,
(2)
where
k
S
is the current level of belief,
1−k
S
is
the belief at the last update,
()
k
xs
is the new
evidence input into the system, and
α
and
β
are
weights to enforce recency or primacy. This model
also supports inertia through the mechanism where
“as information accumulates and as people become
more firmly committed to their beliefs, values of
α
and
β
would decline in a long series of evidence
items” (Hogarth and Einhorn, 1992).
While the goal of a system which integrates
evidence over extended time periods may not be to
replicate these effects in human behavior, these
results should provide cause for us to consider
whether a robust evidential integration paradigm
should have the flexibility to mathematically support
them.
3 EXISTING APPROACHES TO
EVIDENCE COMBINATION
There are numerous approaches in the literature for
evidence combining and Hawthorne observes: “The
issue regarding which kind of factor should be taken
as primitive [for sequential evidence accumulation]
is not a purely mathematical issue. It is an
epistemological, or an empirical, or a pragmatic
issue” (Hawthorne, 2004). We will briefly review
some of them.
3.1 Basic Approaches for Evidence
Combination
The most common approach for evidence
combining is Bayes’ conditioning when new
evidence, E, becomes ‘known’ to be true (Shafer,
1976):
(
)
(
)
EApAp |
12
=
(3)
Another rule of belief revision based on Bayes
conditioning include Jeffrey’s which directly
extends Bayes by allowing for uncertainty in the
options for E (Garber, 1980):
(
)
(
)()
∑
Ω∈
=
e
new
EpEApAp |
12
(4)
Dempster provides an alternative to conditioning
through his rule of combination (Shafer, 1976):
()
() ()
() ()
∑
∑
=
=
∩
∩
−
=⊕
φ YX
ZYX
YmXm
YmXm
Zmm
21
21
21
1 .
.
(5)
where X, Y and Z are the elements of the power set.
Note in all of these approaches there are no
mechanisms for specifically dealing with integrating
temporal streams of data and in particular
discounting information to support either
recency/primacy or long term inertia.
3.2 Extensions of the Basic Theories to
Temporal Evidence Streams
Dempster’s Rule of Combination has been extended
to process a temporal stream of sensor inputs by
viewing m
2
(a) “not as sensor S
j
’s observation, but
instead as the previously combined observations
ACCUMULATING EVIDENCE BASED ON ESTIMATION THEORY AND HUMAN PSYCHOLOGY
377

(Wu, Siegel, & Ablay, 2003):
()
() ()
() ()
∑
∑
=
=
∩
∩
⋅⋅−
⋅⋅
=⊕
φ YX
ZYX
YmwXmw
YmwXmw
Zmm
2211
2211
21
.1
.
,
(6)
where the weights are computed according to:
() ( )
n
n
ii
pTntctw ⋅Δ⋅−=
∑
∞
=0
,
(7)
and c
i
(t) is either 0 or 1 depending on whether the
sensor estimate is correct or not,
T
Δ
is the
incoming data sampling rate, and p controls the
decay rate of samples being considered.
Hawthorne discusses a collection of approaches
to sequential updating based on the basic Jeffrey’s
updating model in Equation (4) (Hawthorne, 2004).
He begins with a basic sequential update model that
is amnestic in that it completely replaces any past
evidence with the most recently gathered. He then
discusses a likelihood-ratio update model which
provides order independence, however this does not
fit well with the objectives of providing a
mathematical means for providing human-inspired
evidential reasoning.
3.3 Alternative Approaches based on
Estimation Theory
Integration of temporal streams of data sources
typically employs estimation techniques. The basic
processing requirements for any estimation system
are highlighted in Figure 1 (Blackman, 1986). For
the purpose of this paper we will focus
predominantly on Filtering, Prediction and Gain
Computation.
Figure 1: General Processing Flow for Estimation System.
For the Filtering task in Figure 1 the simplest
filter is the moving average filter (Nakamura,
Loureiro, & Frery, 2007):
() ()
∑
−
=
−=
1
0
1
ˆ
M
i
ikz
M
kx
,
(8)
where z is the incoming belief stream and x(k) is
the output beliefs. This moving average filter can
be extended to the Finite Impulse Response (FIR)
filter where the sum is replaced by a weighted sum
with coefficients chosen to control the frequency
response of the filter. Dewasurendra, et al developed
filters that integrate beliefs based on their frequency
of occurrence, using (Dewasurendra et al., 2007):
() () ( )
∑∑
=
−
=
−
⋅+⋅=
N
i
iki
N
i
kik
ABBelBBelBBel
11
1
| βα
(9)
and
∑∑
==
=+
N
i
i
N
i
i
11
1 βα
.
(10)
The
α
and
β
are weights which are defined to
produce a desired transfer function for detecting the
frequency behavior of the evidence being analyzed.
The simplest form of estimator which also
incorporates the Prediction processing block in
Figure 1 is the
β
α
−
tracker which is defined as
(Blackman, 1986):
(
)
(
)()()
[
]
kxkxkxkx
predobspredest
−
⋅
+
=
α
(11)
() ()
[
]
kxkx
T
kvkv
predobsestest
−⋅+−=
β
)1()(
(12)
(
)
(
)
)(1 kvTkxkx
estestpred
⋅+
=
+
,
(13)
where
(
)
kx
est
is the estimate for the state x,
(
)
kx
pred
is the prediction of the state at time k,
(
)
kx
obs
is the current observation,
)(kv
est
is the
estimate for the velocity, and
α
and
β
are the fixed
filter gains.
A framework for sequential belief updating that
is based on fixed weights, analogous to the
β
α
−
tracker, has been developed by Premaratne, et al.
(2007), using:
(
)
(
)
(
)
ABBelBBelBBel
kkkkk
|
1111
⋅
+
⋅
=
+
β
α
,
(14)
where the weights are constrained by
1
=
+
kk
β
α
and
(
)
kx
pred
corresponds to
(
)
1
BBel
k
and
(
)
kx
obs
corresponds to
()
ABBel
k
|
1
. Equation
(14) exhibits some of the behavior we tend to expect
in a signal processing framework, namely: “…when
encountered with the same streaming information
continuously, the belief converges to a value
decided solely by this incoming information”
(Premaratne, et al., 2007). The weight selection
controls the relative importance of new versus
historical evidence, thereby also providing support
for primacy and recency.
The Kalman filter is the next step in complexity
for estimation algorithms; however, to date no one
has implemented a quantitative evidence
accumulation system strictly based on the principles
of Kalman filtering. Benferhat, et al. developed an
analogy to the Kalman filter for qualitative belief
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
378

revision within Possibility Theory that (Benferhet et
al., 2000). In the following section we will develop
a complete Kalman filter formalism for evidence
accumulation.
4 PROPOSED STRUCTURE FOR
A KALMAN FILTER FOR
EVIDENCE FILTERING
Let us consider the estimate of a basic evidential
state at some time increment k, to be
()
kx
E
ˆ
and an
incoming measure of such a state to be
(
)
kx
obs
.
Assume an initial estimate of the uncertainty in that
state is defined to be:
2
E
σ
and the uncertainty in the
measurements to be
2
M
σ
. For simplicity we will
assume the state transition matrix and the
measurement matrix are the identity matrices.
The basic estimate update equation would be
(Gelb, 1974):
() ( ) () () ( )
[
] 1
ˆ
1
ˆˆ
−−
⋅
+−= kxkxkGkxkx
EobsEE
.
(15)
Recall in the Hogarth and Einhorn model defined
in Equations (1) and (2), there was a corresponding
term in the brackets which accounted for the
difference between the incoming evidence and a
reference which served as the anchor. In a Kalman-
based approach, the reference is the integrated belief
state.
After each update of the filter we compute a new
estimate for the estimate uncertainty to be (Gelb,
1974):
() ()()()
1
ˆ
1
ˆ
22
−⋅−= kkGk
EE
σσ
,
(16)
where the gain term is simply (Gelb, 1974):
()
(
)
() ()
kk
k
kG
ME
E
22
2
ˆ
ˆ
σσ
σ
+
=
.
(17)
Equations (15) through (17) represent the
simplest form possible for the Kalman filter. Note
however, that the gain term defined in Equation (17)
does not include the desired System Covariance
which captures the uncertainty in the system model.
The measurement and system noise uncertainty
terms parallel the two fundamental types of
uncertainty: Aleatory (relating to traditional issues
of variability) and Epistemic which relates to
ignorance and uncertainty in the state of knowledge)
(Sentz, 2002.).
To add this term we need to note that if there is an
added system error h introduced at time k, and then
the state for that time would actually be (Gelb,
1974):
(
)
(
)()
khkxkx
EE
+
−
=
1
.
(18)
This would then result in the covariance for the state
estimate to be (Gelb, 1974):
(
)
(
)()
kkk
hEE
222
ˆˆ
σσσ +=
.
(19)
The behavior of the gain and the resultant
behavior of the filtering system relative to the system
noise behavior,
2
h
σ
, is not obvious, but referring to
Figure 2 we see that in the traditional Kalman
formalism increases in the system noise result in
increases in gain. This behavior is desirable from a
traditional physical state filtering problem, since if
there is a change in the target behavior that we did
not anticipate in our model, we will need to increase
the gain to be able to maintain a track on the object.
There are two key questions we must address at this
point when extending the Kalman filter to evidence
filtering: (i) what behavior do we want from an
evidential filtering viewpoint, and (ii) what does the
term
(
)
k
h
2
σ
correspond to in the evidential
reasoning domain.
To address these questions we will begin with the
comment from Schubert: “A high degree of conflict
is seen if there is a representation error in the frame
of discernment; while a small conflict may be the
result of measuring error” (Schubert, 2008). Recall
the system noise represents the uncertainty in the
representation. Therefore it is natural to consider the
conflict between two sources of evidence as the
parameter to serve as the system noise measure. The
conflict in evidence is (Shafer, 1976):
(
)()
∑
=∩
=
φ YX
YmXm
2112
.K
,
(20)
We propose there should be a decrease in the gain
of the system in the face of conflict to allow us to
evolve the system of beliefs to provide an estimation
analog to traditional Demspter-Shafer where conflict
is simply removed and the masses re-normalized. If
we substitute
12
2
1 K
h
−= σ
in Equation (19) we get:
(
)
(
)()
kKkk
EE 12
22
1
ˆˆ
−+= σσ
.
(21)
The behavior will be as shown in Figure 3,
increases in conflict result in a reduction in gain
which means; evidence will be added to the system
at a reduced level rather than discarded. As this
conflicting evidence continues to come into the
system (assuming it is a sustained change in
environment), it will become less conflicting as the
ACCUMULATING EVIDENCE BASED ON ESTIMATION THEORY AND HUMAN PSYCHOLOGY
379

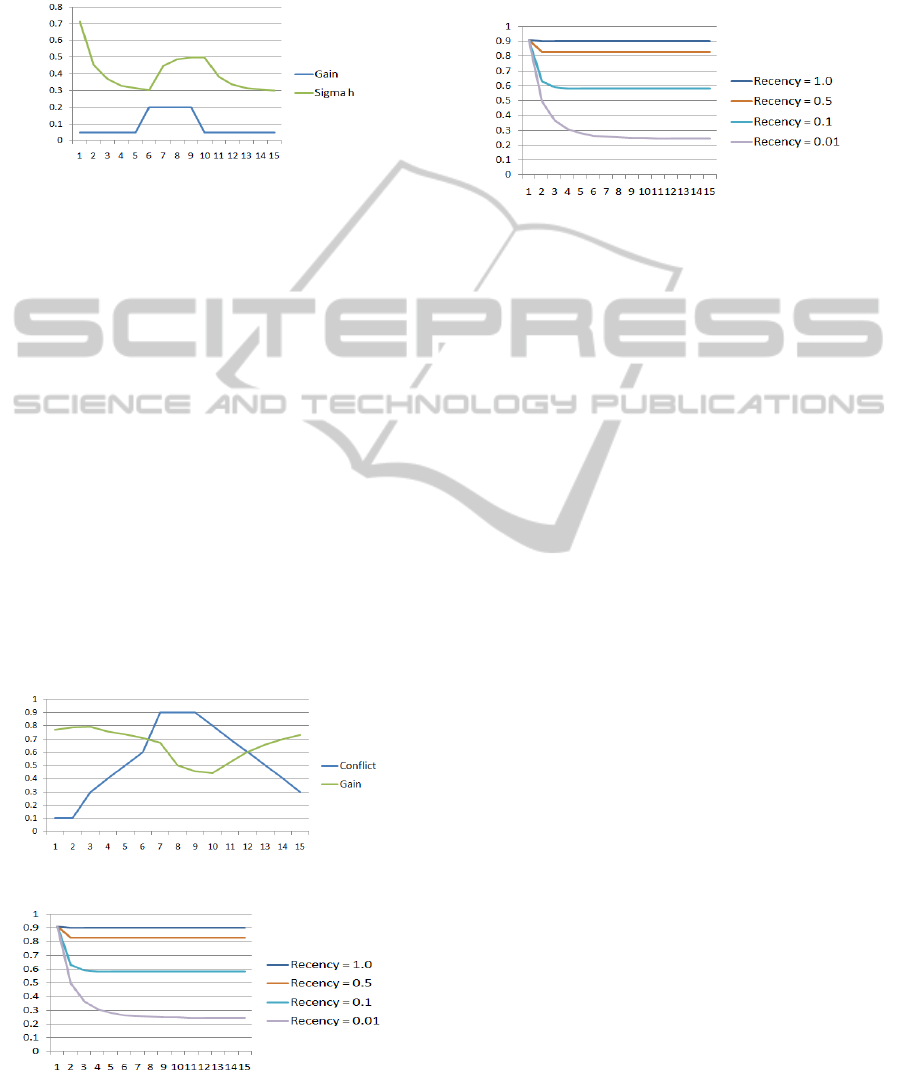
masses evolve, and the gain will increase as the
belief system evolves.
Since one goal of the evidential filter is
supporting desired time order preference we propose
Figure 2: Traditional Kalman gain due to increase in
2
h
σ
.
introducing a term we call the recency factor,
rec
α
,
to Equation (21) to bias the state estimate towards
recency or primacy:
() () ()()
kKkk
recEE 12
22
1
ˆˆ
−⋅+= ασσ
.
(22)
Our rationale for inserting the term into equation
(21) is based on recalling it is derived from the
addition of an offset into the state estimate (recall
Equation (18)), and we are adding to this term with
bias towards past or current measures based on the
desired behavior of the filter for a given application.
Figure 4 provides a set of curves for how the gain
behaves over time for varying recency factors.
Additionally Figure 5 shows the behavior of the gain
for various recency factors when there is a sudden
increase in conflict of the incoming measures with
the existing state, which support our objectives: (i)
higher gain for higher recency, and (ii) reduced gain
during periods of conflict.
Figure 3: Effect on gain with increase in conflict.
Figure 4: Gain versus recency factor,
rec
α
.
There are numerous candidates to serve the role of
2
M
σ
in gain term defined in Equation (17). Recall in
the traditional Kalman filter, the measurement
variance is based on the signal-to-noise ratio of the
Figure 5: Gain versus recency factors,
rec
α
during sudden
increase in conflict.
detected signals. For evidence filtering the most
logical choice is the variance in the classification
measure at each instance.
5 CONCLUSIONS AND FUTURE
WORK
We have reviewed results from evidence
accumulation in human subjects and discovered
there are three key issues when compared to
evidence accumulation in artificial intelligence,
namely: (i) order effects, (ii) evidence impact
reduction in long evidence streams, and (iii)
evidence evaluation versus estimation. Based on
this observation we proposed there is a need for an
alternative estimation theoretic approach to
accumulating evidence over long time streams from
single sensors. We then reviewed various
approaches for evidence accumulation, and showed
the parallelisms between existing evidence filtering
approaches to traditional FIR filters and
β
α
−
trackers and noted there are no systems strictly
based on the Kalman filter. We then developed a
formalism for evidence accumulation based on the
principles of the Kalman filter. We then related the
key Kalman noise terms, namely the measurement
noise and the system noise to the ideas of aleatory
and epistemic uncertainty in evidence accumulation.
As the concept of ignorance corresponds to the
epistemic uncertainty, we propose that the conflict in
the incoming evidential states can be used as a
means of estimating the system noise. The
measurement noise for systems which provide
classification outputs can be estimated the
classification system variance. Future work will be
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
380

directed at further studying the ability to use conflict
as a measure of system noise and to execute these
algorithms on a typical evidence accumulation
problem.
REFERENCES
Baratgin, J., & Politzer, G., 2007. The psychology of
dynamic probability judgment: order effect, normative
theories, and experimental methodology. Mind &
Society. Springer.
Benferhet, S., Dubois, D., & Prade, H., 2000. Kalman-like
filtering in a qualitative setting. INRIA.
Blackman, S. S., 1986. Multiple-target Tracking with
Radar Applications. Artech House.
Dewasurendra, D., Bauer, P. H., & Premaratne, K., 2007.
Evidence filtering. IEEE Trans. On Signal Processing.
IEEE.
Dubois, D., & Prade, H., 1997. A synthetic view of belief
revision with uncertain inputs in a framework of
possibility theory. International Journal of
Approximate Reasoning. Elsevier.
Garber, D., 1980. Discussion: Field and Jeffrey
conditionalization. Philosophy of Science, Philosophy
of Science Association.
Gelb, A., 1974. Applied Optimal Estimation. Cambridge:
MIT Press.
Hawthorne, J., 2004. Three models of sequential belief
updating on uncertain evidence. Journal of
Philosophical Logic. Springer.
Hogarth, R. M., & Einhorn, H. J., 1992. Order effects in
belief updating: The belief-adjustment model.
Cognitive Psychology. Elsevier.
Liu, W., & Hong, J., 2000. Re-investigating Dempster’s
idea on evidence combination. Knowledge and
Information Systems. Springer.
Nakamura, E. F., Loureiro, A. A., & Frery, A. C., 2007.
Information fusion for wireless sensor networks:
Methods, models and classifications. ACM Computing
Surveys. ACM.
Premaratne, K., Dewasurendra, D. A., & Bauer, P. H.,
2007. Evidence combination in an environment with
heterogeneous sources. IEEE. Trans on Systems, Man,
and Cybernetics-Part A: Systems and Humans. IEEE.
Schubert, J., 2008. Conflict management in Dempster-
Shafer theory by sequential discounting using the
degree of falsity. Procs. of Intl. Conf. on Information
Processing and Management of Uncertainty in
Knowledge-based Systems. Elsevier.
Sentz, K., 2002. Combination of evidence in Dempster-
Shafer theory - SAND 2002-0835. SANDIA.
Shafer, G., 1976. A Mathematical Theory of Evidence.
Princeton: Princeton University Press.
Wang, H., Zhang, J., & Johnson, T. R., 1999. Order
effects in human belief revision. Proceedings of the
1999 Cognitive Science Society Conference. Cognitive
Science Society.
Wu, H., Siegel, M., & Ablay, S., 2003. Sensor fusion
using Dempster-Shafer theory II: Static weighting and
Kalman filter-like dynamic weighting. Procs. of
Instrumentation and Measurement Technology
Conference. IEEE.
Zhao, J., & Osherson, D., 2010. Updating beliefs in light
of uncertain evidence: Descriptive assessment of
Jeffrey's rule. Thinking & Reasoning. Taylor &
Francis Group.
ACCUMULATING EVIDENCE BASED ON ESTIMATION THEORY AND HUMAN PSYCHOLOGY
381