CONTROL FOR OTM(ON-THE-MOVE) ANTENNA DRIVEN
BY INDIRECT SERVO MECHANISM WITH FLEXIBILITY
Min Sig Kang
Dept. of Mechanical and Automotive Engineering, Kyungwon University, Bokjung-Dong, Sungnam, Kyunggi-Do, Korea
Jong Kwang Lee, Ki Ho Kim
Korea Atomic Energy Research Institute, Dukjin-Dong, Yuseong-Gu, Daejeon, Korea
Keywords: OTM (on-the-move) Antenna, Satellite Communication, LOS(line of sight) stabilization, Two-inertia
system control, Damping control, Vehicle motion compensation, Roll compensation.
Abstract: In this study, an OTM(On-The-Move) antenna which is mounted on ground vehicles and used for
communication between vehicle and satellite was addressed. Since vehicles move during communication,
active antenna LOS(line-of-sight) stabilization is a core technology to guarantee satellite communication
quality. Stabilization control of the LOS of antenna which is driven by a motor coupled with gear and
flexible driving shaft has been addressed. In the consideration of finite stiffness of the shaft, disturbance
torque due to vehicle motion coupled with gear ratio, and kinematic coupling of the outer gimbal dynamics,
a stabilization control has been proposed. The feasibility of the proposed control design was verified along
with simulation results.
1 INTRODUCTION
Inertially stabilized platforms are used to stabilize
and point sensors, image acquisition devices,
telescopes, weapon systems, etc. These platforms are
usually equipped on various moving vehicles such as
ground vehicles, aircrafts, ships, satellites,
submarines, and are even used on handheld
devices(Hilkert, 2008; Debruin, 2008). This paper
considers an OTM(on-the-move) satellite
communication antenna mounted on a ground
moving vehicle in the control aspects. In this
application, LOS(line of sight) of antenna must be
pointed to a fixed-satellite accurately while the
vehicle on which the antenna is mounted is moving
over a rough terrain to ensure good communication
quality as shown in Fig. 1. To establish these
requirements, a gimbaled platform, suitable sensors
and active control are needed to stabilize the
LOS(line-of-sight) in an inertial frame.
In the aspect of control, direct driven gimbal servo-
mechanism is advisable (Kennedy et al., 2003), but a
motor drive system equipped with gear train and
flexible driving shaft is addressed in this paper.
Certainly this indirect driving mechanism is cost
effective then direct one. On the other hand,
vibration suppression and disturbance rejection is an
important problem in motion control. To overcome
the problems, various control methods were
suggested such as PI, PID, Optimal, Variable
Structural Control, etc. (Nam et al., 2008; Zhang et
al., 2000; Szabat et al., 2007; Hace et al., 2005).
However, though the research of the flexible
transmission control is widely present, the methods
often do not address the load position control
problem, which is a key issue in the LOS
stabilization.
In this paper, we propose a control design
technique which addresses the flexibility of torque
transmission, the disturbance torque coupled with
gear ratio and vehicle motion, and kinematic
coupling that is inherent problem of all two-axis
gimbals. The effectiveness of the proposed control is
established along with some simulation examples.
2 DYNAMIC MODEL OF
GIMBAL SYSTEM
A commonly used configuration for OTM antenna
227
Sig Kang M., Kwang Lee J. and Ho Kim K..
CONTROL FOR OTM(ON-THE-MOVE) ANTENNA DRIVEN BY INDIRECT SERVO MECHANISM WITH FLEXIBILITY.
DOI: 10.5220/0003571202270230
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 227-230
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

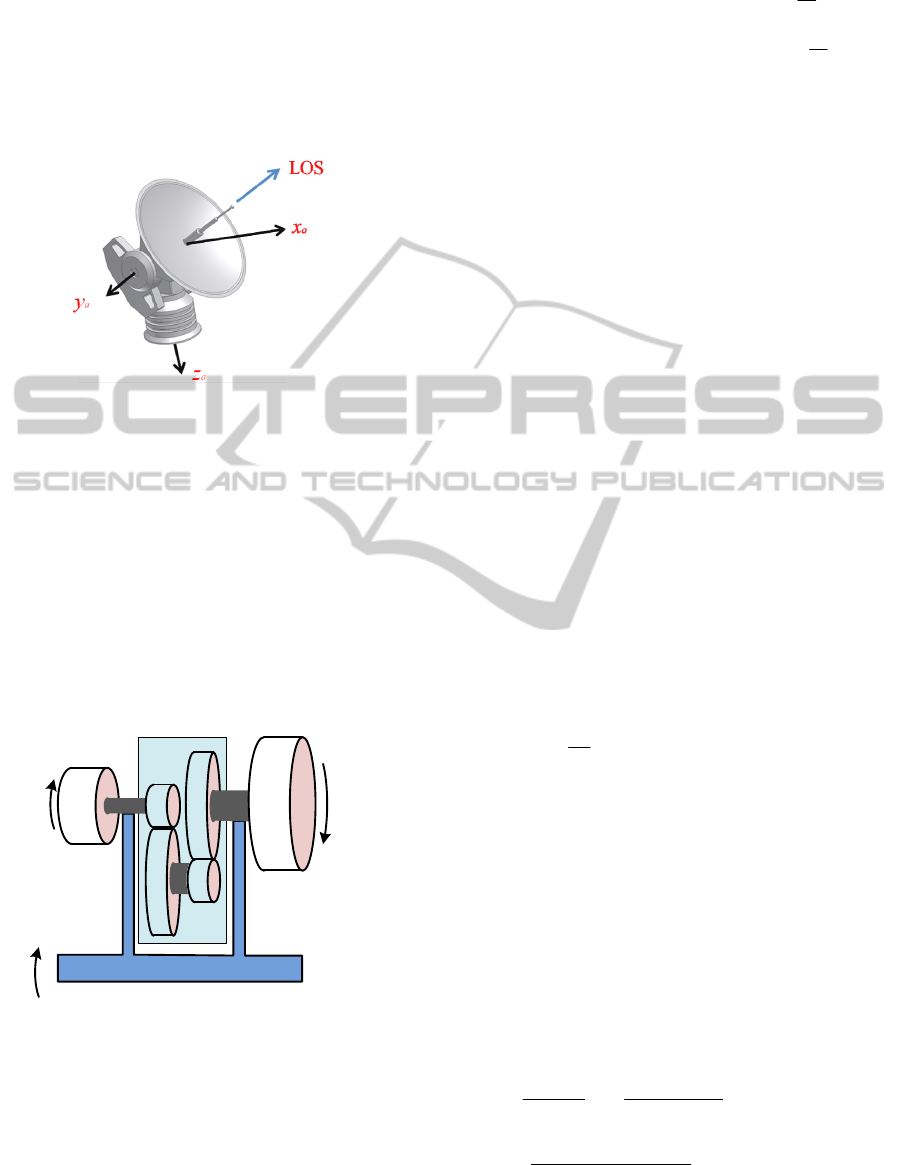
suspended by a two-axis gimbal (elevation over
azimuth) system is illustrated in Fig. 1. The gimbal
axes are orthogonal each other. An antenna
comprised of an aperture and a supporting device is
used to collect and direct RF energy from and to the
satellite. A dish type aperture is used in a traditional
antenna.
Figure 1: Structure of OTM Antenna.
To drive the antenna in Fig.1, two motors are used:
one for the inner gimbal and the other for outer
gimbal. A driving mechanism consists of a motor, a
gear of gear ration N, a flexible shaft and load is
shown in Fig. 2. Throughout this paper the
subscripts
m
and L denote the motor and load,
respectively. J is the moment of inertia, and
ω
is the
angle velocity measured in inertial space.
h
ω
is the
vehicle rotation.
1
k
and
2
k
are stiffness of the motor
axis and the gear train output axis, respectively.
M
otor
Gear Train
N
1
k
2
k
m
J
m
m
T
ω
1
ω
h
ω
Load
L
L
T
ω
L
J
Vehicle
Figure 2: Schematic of gimbal driving mechanism.
To measure the pitch rate and yaw rate of the LOS, a
set of orthogonal two-axis rate gyro is mounted on
the antenna.
If the moment of inertia of the gear train is small
enough compared with those of motor and load, then
the dynamic model can be represented by a two-
inertia system as follows:
2
(1)
(1)
mm eqm eqL eq h m
L L eq L eq m eq h d
d
JK NK KN T
dt
d
JNK NK KNN T
dt
ωω ω ω
ωωω ω
⎧
+− =−−+
⎪
⎪
⎨
⎪
+−=−+
⎪
⎩


(1)
where
()
2
12 1 2
/
eq
KkkNkk=+is the equivalent
stiffness represented in the motor side.
As can be seen in (1), vehicle motion coupled with
gear ratio and equivalent stiffness affects as a torque
disturbance on both the motor and load dynamics.
3 STABILIZATION CONTROL
3.1 Elevation Axis
The objective of stabilization control for antenna
pitch-direction is absolutely nullifying the inertial
angular rate of the load, i.e.
0
a
Ly
ωω ==
. Thus the
inner gimbal remains mass stabilized and does not
need to move in inertial space to stabilize the LOS,
and merely needs to drive to nullify the pitch rate
gyro output.
To stabilize the model in (1) which has two vibration
modes of no damping, we introduce a conventional
IPD-control(
IPD
T
) + damping-control(
damp
T ) +
vehicle motion feedforward compensation control
(
vffc
T ) of the form
m IPD damp vffc
TT T T
=
++
()
()
*
i
IPD r L d p L
K
TKsK
s
ωω ω =−−+
{}
(1)
damp m m h L
TK N N ωωω =− + − −
ˆ
(1)
vffc m h
TNJ ω =− −

(2)
where
r
ω is the reference rate input and
ˆ
h
ω

denotes
the measured or estimated vehicle angular
acceleration. The term in the parenthesis of the
damping control implies relative twisting rate of the
shaft between the motor and the load.
Applying the control (2) to the system (1) gives the
closed-loop model as
{}
{}
2
(1)
() ()
()
eq i eq
Lr mhh
mmeq
d
NK K N N K
J
ps ps
sJs Ks K
T
ps
ωω ωω
−
=+ −
++
+



(3)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
228

43 2 2
2
() ( )
()
mL L m L m d eq
m p eq eq i
p
sJJsJKs J NJ NKKs
N K NK K s NK K
=++++
++ +
(4)
From (3), we can see that the stabilization error due
to vehicle motion can be reduced by the vehicle
motion compensation. Certainly, from the closed-
loop characteristic equation
()ps , the damping
control gain
m
K
is necessary to stabilize the system.
To design control gains, we employ a simple pole-
assignment technique as follows:
()
2
22
() 2
mo n n
ps J J s ςω ω =++
(5)
where
ς
and
n
ω
are the desired damping ratio and
natural frequency, respectively.
The control gains can be easily determined from (4)
and (5).
3.2 Azimuth Axis
Apart from the inner gimbal, the outer gimbal axis
does not coincide with the antenna yaw axis. Thus
the outer gimbal must be rotated to stabilize the LOS
because of the kinematic coupling that is inherent
problem of all two-axis gimbals.
Figure 3: Yaw rate of LOS.
More precisely, as shown in Fig. 3, to stabilize the
LOS, the outer gimbal must rotate to nullify yaw
rate of the LOS. From the kinematic coupling, the
yaw rate is given by
cos sin
yaw EL outer EL roll
ω
θω θω =+
(6)
where
y
aw
ω
is the yaw rate of the LOS,
roll
ω
is the
roll rate of the outer gimbal, and
E
L
θ
the inner
gimbal angle.
Consequently, from (6), the outer gimbal rate should
satisfy the following to stabilize the LOS.
tan
outer EL roll
ω
θω =−
(7)
In other words, the kinematic coupling has the same
effect on the apparent motion of LOS as a torque
disturbance acting in the opposite direction.
In the consideration of the kinematic coupling, the
control in (2) is modified to include secant gain
correction and roll motion compensation as follows:
m IPD damp vffc roll
TT T T T
=
+++
()
()
*
1
cos
i
I
PD r yaw d p yaw
EL
K
TKsK
s
ωω ω
θ
⎡
⎤
=−−+
⎢
⎥
⎣
⎦
{
}
(1)
damp m m h outer
TK N N ωωω =− + − −
ˆ
(1)
vffc m h
TNJ
ω
=− −

2
tan
()
EL
roll L m roll
TJNJs
N
θ
ω
⎧⎫
=− +
⎨⎬
⎩⎭
(8)
Then the closed-loop yaw rate is given by
{
}
{}
3
,
2
,
sin
() ()
cos
()
eq m i
mo o m
y
aw r EL roll
mmeqmEL
d
NK K
sJJsJK
ps ps
sJs Ks K
T
ps
ω
ωθω
θ
+
=+
++
+
(9)
Without the roll compensation in (8), the closed-
loop yaw rate due to the coupling is given as
{
}
22 2
()
sin
()
mL o m L m eq
yaw EL roll
roll
sJJs JKs J NJK
ps
ω
θω
+++
=
(10)
Comparing (9) with (10), we can expect the roll
compensation can attenuate stabilization error due to
the kinematic coupling.
4 SIMULATION EXAMPLES
To evaluate the feasibility of the proposed control,
some simulations were carried for the outer gimbal
of the OTM antenna under consideration. A
controller was designed according to the method in
the previous section. Throughout the simulations,
the sampling frequency was kept at 1 kHz.
Some simulation results conformed the damping
control is necessary to stabilize the system. Also we
found that the vehicle motion compensation can
perfectly cancel the disturbance torque coupled with
gear ratio and vehicle angular acceleration when the
vehicle acceleration is measured accurately.
To establish the stabilization performance of the
roll motion compensation, a response to a typical
vehicle motion were simulated. For the simplicity,
the angular acceleration of the vehicle roll motion
was assumed to be a chirp signal of which frequency
varies linearly from 0.1Hz to 5Hz within 5 s. The
magnitude of the acceleration at each frequency was
kept to be 10 rad/s
2
. The elevation angle was
assumed to be 45
o
. Fig. 4 shows the stabilization
error resulted from the controls with and without the

1
o
J
s
outer
ω
cos
E
L
θ
sin
E
L
θ
roll
ω
d
T
yaw
ω
CONTROL FOR OTM(ON-THE-MOVE) ANTENNA DRIVEN BY INDIRECT SERVO MECHANISM WITH
FLEXIBILITY
229

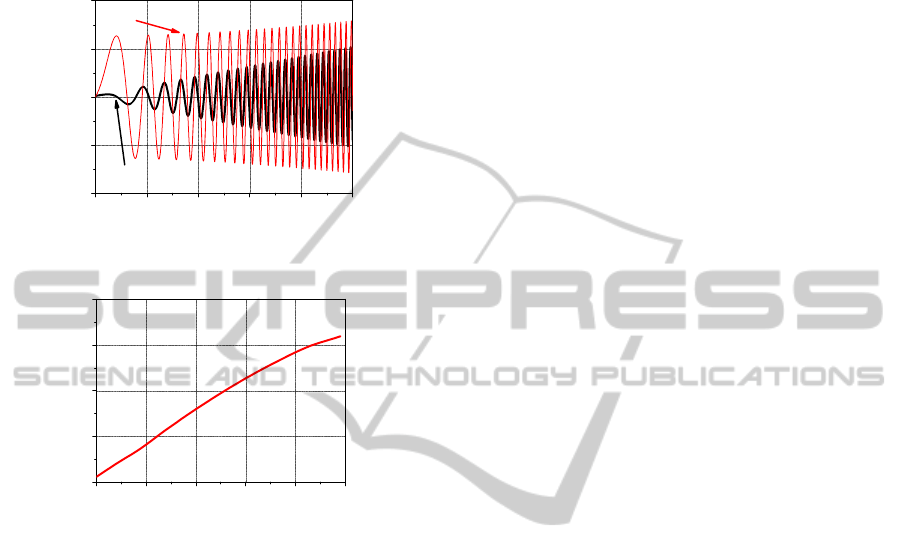
roll compensation. As expected from (9) and (10),
the responses exhibited the effectiveness of the roll
compensation for attenuating stabilization error due
to the gimbal kinematic coupling.
Figure 4: Stabilization error – azimuth direction.
Figure 5: Stabilization error attenuation ratio.
The stabilization error ratio which calculated
from the magnitude of error with compensation over
the magnitude of error without compensation is
shown in Fig. 5. Evidently, the error is largely
attenuated in low frequency region, and the lesser as
increasing frequency. This result is consistent with
the analytical results in (9) and (10). From the
simulation results, we can conclude the control
proposed in this paper is effective to improve
stabilization performance of OTM antenna.
5 CONCLUSIONS
In this work, an inertial stabilization control for the
LOS of an OTM antenna driven by a motor coupled
with gear and flexible driving shaft has been
addressed. In the consideration of flexibility of the
shaft, disturbance torque due to vehicle motion
coupled with gear ratio, and kinematic coupling of
the outer gimbal dynamics, a stabilization control
has been proposed. The control consists of a
conventional IPD-control, damping-control, vehicle
motion feed-forward compensation-control, and roll
motion feed-forward compensation control.
The simulation results demonstrated that the
proposed control design guarantees system stability
and effective to attenuate the stabilization error due
to the disturbance torque related to vehicle motion
and kinematic coupling.
ACKNOWLEDGEMENTS
This work was supported by Nuclear Research &
Development Program of National Research
Fundation(NRF) funded by Ministry of Education,
Science & Technology(MEST) and the Kyungwon
University Research Fund in 2011.
REFERENCES
Hilkert, J. M., Inertially stabilized platform technology:
concept and principles, IEEE Control Systems
Magazine, pp. 26-46, 2008.
Debruin, J., Control systems for mobile satcom antennas,
IEEE Control Systems Magazine, pp. 86-101, 2008.
Kennedy, P. J. and Kennedy, R. L., Direct and indirect
line of sight(LOS) stabilization, IEEE Trans. on
Control Systems Technology, Vol. 11, No. 1, pp. 3-15,
2003.
Nam, B. U., Kim, H. S., Lee H. J., and Kim, D. H.,
Optimal speed controller design of the two-inertia
stabilization system, World Academy of Science,
Engineering and Technology 41, pp.155-160, 2008.
Zhang, G. and Furusho, J., Speed control of two-inertia
system by PI/PID control, IEEE Trans. of Industrial
Elevtronics, Vol. 47, No. 3, pp.603-609, 2000.
Szabat, K. and Orlowalska, O., Vibration suppression in a
two-mass drive system using PI speed controller and
additional feedback-comparative study, IEEE Trans.
of Industrial Elevtronics, Vol. 54, No. 2, pp.1193-1206,
2007.
Hace, A., Jezernik, K., and Sabanovic, A., Improved
design of VSS controller for a linear belt-driven
servomechanism, IEEE/ASME Trans. on
Mechatronics, Vol. 10, No. 4, pp.385-389, 2005.
0246810
-0.2
-0.1
0.0
0.1
0.2
012345
Frequency [Hz]
W/ Roll Compensation
Angle [mrad]
Time [s]
W/O Roll Compensation
012345
0.0
0.2
0.4
0.6
0.8
Attenuation Ratio
Frequency [Hz]
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
230