SENSOR FAULT DETECTION IN A REAL HYDRAULIC SYSTEM

USING A CLASSIFICATION APPROACH

Oriane Le Pocher, Eric Duviella

Univ. Lille Nord de France, F-59000 Lille, France

EMDouai, IA, F-59500 Douai, France

Karine Chuquet

VNF - Service de la navigation du Nord Pas-de-Calais, 37 rue du Plat, 59034 Lille Cedex, France

Keywords:

Supervision, Fault detection, Classiﬁcation algorithm, Large scale system, Hydraulic system.

Abstract:

This paper focuses on the sensor fault detection of a hydraulic channel used for navigation. This system has the

particularities to have large scale dimension, without slope, with several inputs and ouputs, and thus difﬁcult

to be modelled according to classical modelling methods. For recent years, it was equipped with level sensors

in order to have better knowwledge of its behavior, to detect its state online and thus improve its management.

However, level sensors are subjected to measurement or transmission errors, setting errors, and quick or slow

drifts. In order to detect these sensor errors, a classiﬁcation approach is proposed. It appears adapted to the

fault detection of large scale hydraulic systems without model. The classiﬁcation approach is used on data

measured from 2006 to 2009. The ﬁrst results and analysis show that the classiﬁcation method is effective for

addressing the problem of sensor fault detection.

1 INTRODUCTION

Hydrographical networks are large scale systems

characterized by nonlineardynamics and varying time

delays. They are used for several human activities,

especially navigation and transport. In the northern

Europe, navigation channels assure the transport of

goods with the objective, within a few years, of ac-

comodating large broad gauge boats. The control of

the water level in navigation channels becomes cru-

cial. In order to achieve this objective, sensor net-

works have been implemented. These sensors allow

the measurement of water levels or water discharges,

and the implementation of levelcontrol algorithms for

a local water management. At a larger scale, the level

and discharge measurements are essential to provide

an efﬁcient water management of the navigation chan-

nel networks, by mainly characterizing their state on-

line. However, sensor networks are impacted by mea-

sure errors, transmission faults, or drifts of operation.

So, in order to improve the management of navigation

channels, sensor fault detection techniques have to be

employed.

Fault Detection and Isolation (FDI) techniques

are largely proposed in the litterature and employed

by following a systematic approach. The ﬁrst step

consists in characterizing the operating modes of the

system to be supervised. Several model-based ap-

proaches were proposed (Frank et al., 2000), based

on parameters identiﬁcation technique (Weihua et al.,

2003), parity equations method (Gertler, 1998), diag-

nosis observers (Akhenak et al., 2004), or Kalman ﬁl-

ters (Xie et al., 1994). Even if these FDI techniques

have proven to be as powerful and effective, they re-

quire an accurate model of the system by minimizing

the uncertainties and the process noise. Very recently,

fault detection methods based on residual generation,

extended Kalman ﬁlter and ﬁnite memory observer

are proposed in (Bedjaoui and Weyer, 2010), in order

to detect and localize leak in an irrigation network.

This detection method is based on physical hydraulic

system model, in particular on the Saint-Venant par-

tial differential equations (Chow et al., 1998). How-

ever, due to their physical characteristics, i.e. large

dimensions, no slope, etc., navigation channels can

not always be modelled using physical laws without

requiring numeric models. In this way, traditionnal

FDI techniques cannot reach the fault detection aims.

When the physical modelling of the system is

not realizable, pattern recognition techniques consti-

382

Le Pocher O., Duviella E. and Chuquet K..

SENSOR FAULT DETECTION IN A REAL HYDRAULIC SYSTEM USING A CLASSIFICATION APPROACH.

DOI: 10.5220/0003571603820387

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 382-387

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

tute an interesting alternative approach for fault de-

tection problem. They consist in extracting informa-

tion on the system state by using the signals collected

from sensors (Hartert et al., 2010). The operating

modes of the system are represented by classes which

are built according to dynamic classiﬁcation algo-

rithms, as the CDL algorithm (Cluster Detection and

Labeling), algorithms based on adaptive resonance

theory (ART) networks (Su and Liu, 2005), (Eltoft

and de Figueiredo, 1998), FMC algorithm (Fuzzy

Min-max Clustering) (Mouchaweh et al., 2002) or

AUDyC (Auto-Adaptive Dynamical Clustering) al-

gorithm (Lecoeuche et al., 2004). In (Traore et al.,

2009), the AUDyC algorithm is employed to super-

vise a thermo-regulator system subjected to slow and

quick drifts in its dynamics.

This paper focuses on sensor fault detection of the

Cuinchy-Fontinettes navigation channel. This sys-

tem, located in the north of France, is characterized

by large dimensions and no slope. Thus, it is not pos-

sible to be modelled according to physical approach.

Thus, a classiﬁcation approach is proposed to address

the fault detection problem. In section II, the real hy-

draulic system and the problem of sensor fault detec-

tion are presented. The classiﬁcation approach based

on AUDyC algorithm is detailed in section III. This

fault detection technique allows the determination of

indicators characterizingthe real-time drift of sensors.

Finally, in section V, the proposed approach is applied

on real data measured from 2006 to 2009, and its per-

formance for the detection of sensor faults are high-

lighted.

2 PROBLEM STATEMENT

The channel studied is the reach Cuinchy-Fontinettes

which is located in the North of France between the

lock of Cuinchy at the East of the town Bethune and,

at the Southwest of the town Saint-Omer, the lock of

Fontinettes (see Figure 1). With 42.3 km long and

51.8 m large, this reach is part of the broad gauge

river network of North of France. It is characterized

by no signiﬁcant slope. It can handle boats until 185

m long and 11.4 m large. This channel is entirely arti-

ﬁcial. The ﬁrst part of the channel, i.e. 28.7 km from

Cuinchy to Aire sur la Lys, is called ”canal d’Aire”

and has been built in 1820. The second part of the

channel, i.e. 13.6 km from Aire sur la Lys to Saint

Omer, is called ”canal de Neuffoss´e” and has been

built in the eleventh century.

The Cuinchy-Fontinettes is managed by VNF

(Voies Navigables de France). The role of VNF is

to maintain the level of the channel at NNL = 19.52

m to allow the navigation (NNL = Normal Naviga-

tion Level). The main issue for the management of

this reach is to counterbalance the navigation ﬂow

of 3 m

/s at Fontinettes. A part of the water comes

from the navigation ﬂow at Cuinchy which represents

0.6 m

/s. The difference between the two navigation

ﬂows comes from the size of the lock at Fontinettes

which is 13 m high whereas the lock at Cuinchy is

only 2 m high. The counterpart of water comes from

different hydrants and discharges. A high number of

rivers are inverted siphon and pass under the reach

but three of them feed directly the reach. Another

solution to feed the reach is the Cuinchy gate. This

gate allows a controlled feeding of the reach with the

water of the Deˆule river. In the same way, the gate

called ”Porte de Garde” at Aire sur la Lys allows con-

trolled exchanges between the Lys river and the reach.

Finally a high number of anthropogenic discharges

(more than 320) feed the reach in an unknown way.

Fontinettes Lock

Gate ‘Porte de Garde’

Cuinchy lock

Fort Gassion lock

Aire basin

Fort Gassion gate

Fontinettes level sensor

Aire level sensor

Cuinchy level sensor

Figure 1: Scheme of the navigation canal Cuinchy-

Fontinettes.

For recent years the reach has been equipped with

level sensors in order to better know its behaviour.

The level sensors used for this study are located

downstream from the lock of Cuinchy, upstream from

the lock of Fontinettes and in the Aire basin. The

Cuinchy and Aire sensors are composed of an ultra-

sonic transducer linked with a level transformer. The

Fontinettes sensor is a Probe with a transducer inte-

grated. The technology used is based on ultrasonic

sound and allows the processing of echoes. The data

processing and transmission are realized by telepro-

cessing equipments. The three sensors deliver the

mean of the levels measured every quarter hour. The

waves due to navigation or Fontinettes lock opera-

tions are averaged.

Sensors are subjected to the weather and the en-

vironment and as every electronic device can break

down or be impacted over time. Several types of er-

rors can occur. A bad setting of the sensors can lead to

systematic errors. Aberrant data are caused by local

and temporal errors. Blockade of data can be due to

SENSOR FAULT DETECTION IN A REAL HYDRAULIC SYSTEM USING A CLASSIFICATION APPROACH

383

a transmission fault for example. Level sensor can be

subjected to slow temporal drifts. In order to use re-

liable measured data, it is essential to propose a fault

detection technique.

The main problem for the fault detection tech-

nique proposal is the major difﬁculty of modeling

the Cuinchy-Fontinettes channel without numeric ap-

proach. A fault detection technique by a pattern

recognition approach is proposed in the next section

in order to be freed from a model of the channel.

3 FAULT DETECTION BY A

PATTERN RECOGNITION

APPROACH

The fault detection method proposed in this paper is

based on a classiﬁcation technique. This classiﬁca-

tion technique consists in characterizing an operating

mode of the dynamic system by a Gaussian model

which constitutes a class. A class is determined ac-

cording to pertinent selected data which present same

similarities. According to these selected data, a Rep-

resentation Space can be built, and the class can be

represented in this space. Thus, the class of the nor-

mal operating mode, denoted C

, can be determined

(see Figure 2). A new class is create when a sufﬁcient

number of points is present in an area of the Represen-

tation Space. The new class, which is updated or cre-

ated, is denoted evolutionary class C

. It corresponds

to a new operating mode.

When a measurement or transmission error oc-

curs, a new point appears in the Representation Space

far from the normal class C

(see Figure 2.a). This

point has to be detected and rejected if it is isolated.

When the level sensor is subjected to slow drifts, the

class updates online (see Figure 2.b). The character-

istics of the normal class evolve during time. Finally,

catalectic failures lead to a jump in the representation

space (see Figure 2.c).

(a)

(b)

(c)

Figure 2: (a) Measurement or transmission errors, (b) slow

drifts, (c) jump characterising catalectic failure, in a two

dimensions representation space.

The classiﬁcation technique which is proposed to

monitor slow drifts and jumps, is based on the AU-

DyC algorithm. AUDyC is an evolutionary data clas-

siﬁcation algorithm whose role is to model, in a con-

tinuous way, the operating modes of dynamical sys-

tems. The technique is inspired from the mixed Gaus-

sian model (Lecoeuche et al., 2004). The Gaussian

classes are represented by prototypes P

characterized

by a center and a matrix of covariance. The proto-

types characteristics are adapted to each new obser-

vation X = (x

, x

, ... x

), with n the number of per-

tinent data, by using rules of recursive update on a

sliding window of size N

fen

, and by considering the

totality of the prototype P

, noted Card (P

) on previ-

ous instant k− 1, according to the algorithm described

below. A new observation X is rejected if is too far

from the current class. In other case, this observation

is assigned to one of the N existing classes according

to an adaptation procedure of the prototypes.

• If Card(P

)=nb < N

fen

: add information











(k) = M

(k− 1) +

nb+ 1

− M

(k− 1)),

Ω

(k) =

nb− 1

Ω

(k− 1)+

nb+ 1

− M

(k− 1))

⊤

− M

(k− 1)).

(1)

• If nb ≥ N

fen

: add or retreive information











(k) = M

(k− 1) +

fen

(δX

− δX

−

Ω

j (k) = Ω

j (k− 1)+

∆X







fen

−1)

fen

−1)

−

fen

+1)

fen

−1)







∆X

⊤

(2)

where







δX

= X

new

− M

(k− 1),

δX

−

= X

old

− M

(k− 1),

∆X = [δX

δX

−

(3)

with M

(k) and Ω

(k) respectively the center and

the covariance matrix of the prototype P

at instant k,

fen

the width of the slipping window, X

new

and X

old

new and old observation vectors, respectively.

This fault detection method based on AUDyC al-

gorithm allows rejecting measurement or transmis-

sion errors, following slow drifts and catalectic fail-

ures. In order to detect drifts, fault indicators have

to be calculated. A ﬁrst indicator corresponds to the

mean of the measured levels on the sliding window

fen

. It allows the visualisation of quick and slows

drifts. A second indicator consists in computing the

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

384

distance between the evolutive class C

and the nor-

mal class C

. The normal class is taken as reference.

A fault occurence can lead to the drift of the evolu-

tive class C

from the normal class C

. Increasing of

this distance reveals, in some cases, the presence of

faults. Amongst the several existing metrics, the Eu-

clidian distance, denoted d(M

), is considered:

d(M

) =

− M

)(M

− M

)

⊤

, (4)

with M

is the center of the class C

and M

the center

of the normal classC

. The center of the normal class

is ﬁxed.

Moreover, by considering, for causal systems, that

the outputs depend on the variation of the inputs, cor-

relation indicators between the center of the evolutive

class according to each direction of the Representa-

tion Space, denoted K

i, j

for data x

and x

, can reveal

a fault occurence. That leads to compute correlation

coefﬁcients between the mean of each measured level

on a sliding window of size N

fen

. In a second step, er-

ror indicators are computed between the center of the

evolutive class amongst each direction of the Repre-

sentation Space also. The error indicators are denoted

i, j

for data x

and x

. Finally, the quadratic error in-

dicators ε

i, j

are computed according to ε

i, j

Quadratic error indicators ε

i, j

are used in order to

detect setting errors. Error indicators ε

i, j

are used in

order to detect slow drifts and to determine which sen-

sor is faulty. Finally, correlation indicators K

i, j

al-

low the detection of quick drifts and catalectic fail-

ures. The redondancy of the indicators and a cross-

comparison lead to determine which of the sensors is

faulty. The fault detection approach is applied in the

case of the Cuinchy-Fontinettes Channel on data from

2006 to 2009. Results and analysis are presented in

the next section.

4 FAULT DETECTION IN THE

CUINCHY-FONTINETTES

CHANNEL

Measured data on the Cuinchy-Fontinettes Channel

correspond to x

, x

and x

, for Aire in the middle

of the channel, for Cuinchy at the upstream, and for

Fontinettes at the downstream, respectively. These

data are measured with a sample time equal to 15

minutes from 2006 to 2009. It represents more than

135000 × 3 values. These data were not recorded at

the same time. Indeed, there are discrepancies of few

minutes between measurements. Then, the ﬁrst step

is to resynchronize all the data.

The second step consisted in building the Repre-

sentation Space with the three measured data x

, x

and x

, and to represent the normal class C

(see Fig-

ure 3). The normal class is built with accurate mea-

sured data from April to June 2006 according to a slid-

ing window N

fen

equal to 2500 values. The center of

the class C

is around zero (relative levels according

to the NNL), i.e. [−0.034 − 0.058 − 0.059], and its

covariance matrix is equal to:





0.0060 0.0052 0.0055

0.0052 0.0055 0.0052

0.0055 0.0052 0.0065





. (5)

Figure 3: Normal class C

in the Representation Space.

Although the total measured data was used, only

years 2006 and 2009 were shown to highlight the per-

formance of the proposed approach. Figure 4 shows

the measured levels, i.e. x

, x

and x

, and the de-

tection and isolation of wrong measured data during

the year 2009. The wrong data are depicted by black

cross in Figure 4. The classiﬁcation approach allows

to reject these points automatically.

Figure 4: Data x

(continuous line), x

(dotted line) and x

(dashed-dotted line) measured on 2009, and isolate wrong

data (black cross).

Figure 5.a shows the measured levels in Cuinchy

(blue continuous line), in Aire (red dashed line)

and in Fontinettes (green dashed-dotted line) during

2009. The distance d(M

) is depicted in Figure

SENSOR FAULT DETECTION IN A REAL HYDRAULIC SYSTEM USING A CLASSIFICATION APPROACH

385

5.b. The correlation indicators K

c,a

, K

c, f

and K

a, f

the quadratic error indicators ε

c,a

, ε

c, f

and ε

a, f

, and

the error indicators ε

c,a

, ε

c, f

and ε

a, f

, are computed

between the mean of measured levels in Cuinchy

and Aire, in Cuinchy and Fontinettes, in Aire and

Fontinettes, respectively. Indicators between Cuinchy

and Aire are depicted in blue continuous line, those

between Cuinchy and Fontinettes in red dashed line,

and those between Aire and Fontinettes in green

dashed-dotted line, in Figure 5.c, 5.d and 5.e, respec-

tively. A threshold deﬁned equal to 0.7 is considered

in order to detect fault when one of the correlation

indicators is under this threshold (see Figure 5.c).

−0.1

0.1

0.2

(a)

Level mean [m]

−0.3

−0.2

−0.1

(b)

0,5

(c)

i,j

0.01

0.02

(d)

i,j

0 1 2 3 4 5 6 7 8 9 10

x 10

−0.05

0.05

0.1

0.15

(e)

i,j

Time [step]

Figure 5: (a) Measured levels x

(continuous line), x

(dot-

ted line) and x

(dashed-dotted line), (b) Euclidienne dis-

tance d

), (c) correlation indicators K

c,a

(continu-

ous line), K

c, f

(dashed line) and K

a, f

(dashed-dotted line),

(d) quadratic error indicators ε

c,a

(continuous line), ε

c, f

(dashed line) and ε

a, f

(dashed-dotted line), (e) error in-

dicators ε

c,a

(continuous line), ε

c, f

(dashed line) and ε

a, f

(dashed-dotted line), measured on 2009.

During 2009, by considering the distance

d(M

) (see Figure 5.b), only one period around

the 90000

step, is relevant to signiﬁcant drift of the

class C

. However, around the 90000

sample, oth-

ers indicators are close to their objective values. This

means that there is no fault. In this period, the dis-

tance d(M

) is increasing because there is a mod-

iﬁcation of the operating mode, which can be the con-

sequence of ﬂood (see measured levels in Figure 5.a).

Figure 5.c shows three periods where correlation in-

dicators are under the ﬁxed threashold, i.e. around

20000

, 66000

and 88000

samples. For the two

ﬁrst periods, there are no signiﬁcant errors ε

and ε

(see Figure 5.d, 5.e). During the third period around

the 88000

sample, there are signiﬁcant errors ε

c, f

a, f

, ε

c, f

and ε

a, f

. Errors ε

c,a

,and ε

c,a

are close to

their objectives. This is relevant of slow drift on the

level sensor in Fontinettes.

Figure 6 shows the measured levels, i.e. x

, x

and x

, during the year 2006. The detected wrong

measured data appear during the period around the

55000

sample (see black cross).

0 1 2 3 4 5 6 7 8 9 10

x 10

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

Time [steps]

Level [m]

Figure 6: Data x

(continuous line), x

(dotted line) and x

(dashed-dotted line) measured on 2006, and isolate wrong

data (black cross).

The same indicators are determined for year 2006

and depicted in Figure 7, and the same conclusions

can be obtained if the distance d(M

) and corre-

lation indicators are taken into account. The most in-

teresting point to show is the detection of slow drift

of the Cuinchy level sensor during all the year. From

the beginning of year 2006 to the 26000

sample,

quadratic errors ε

c,a

and ε

c, f

are constant and around

0.0025 and ε

a, f

is close to zero (see Figure 7.d). It

means that there is a setting error on the level sensor

in Cuinchy. The setting error is evaluated from 0.05 m

according to the errors ε

c,a

and ε

c, f

(see Figure 7.e).

Then from the 26000

sample to the 65000

sam-

ple, all the errors are close to zero. It is possible to

assume that the Cuinchy level sensor is correctly set.

Finally, from the 65000

sample, quadratic errors ε

c,a

and ε

c, f

are increasing. It is relevant of slow drift of

the Cuinchy level sensor. Errors ε

c,a

and ε

c, f

are de-

creasing to reach −0.1 m.

The fault detection method proposed in this article

allows the detection of error setting, slow and quick

drifts. It can be implemented online in order to detect

these types of faults in real-time.

5 CONCLUSIONS

The sensor fault detection of real large scale systems

without model is an interesting research problem. The

well-known classical FDI techniques cannot be ap-

plied due to the difﬁculty of modelling. Thus, a fault

detection approach without model is proposed in or-

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

386

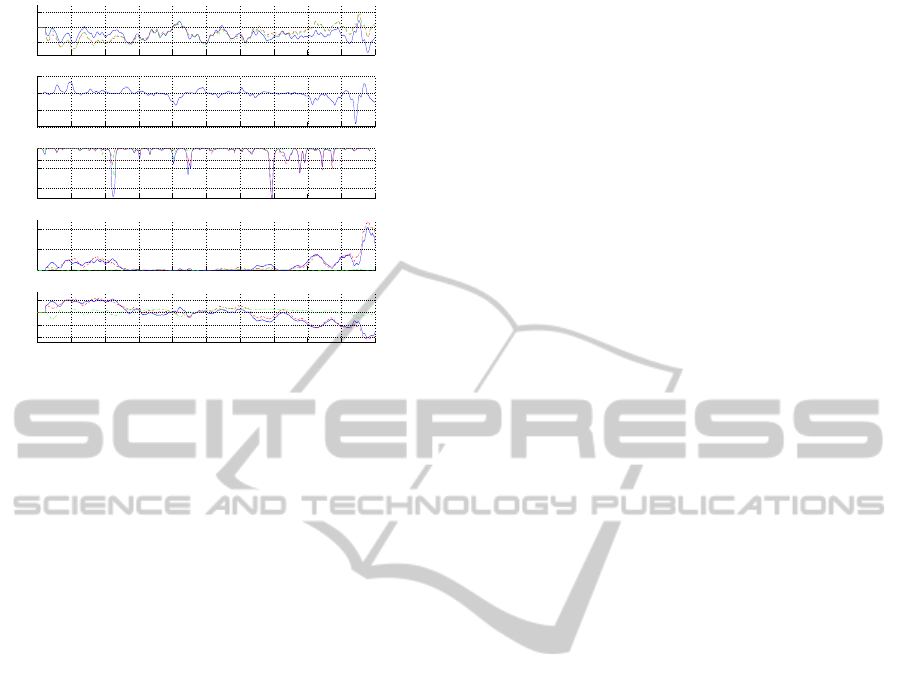
−0.1

0.1

(a)

Level mean [m]

−0.06

−0.03

0.03

(b)

0,5

(c)

i,j

0.005

0.01

(d)

i,j

0 1 2 3 4 5 6 7 8 9 10

x 10

−0.1

−0.05

0.05

(e)

i,j

Time [step]

Figure 7: (a) Measured levels x

(continuous line), x

(dot-

ted line) and x

(dashed-dotted line), (b) Euclidienne dis-

tance d

), (c) correlation indicators K

c,a

(continu-

ous line), K

c, f

(dashed line) and K

a, f

(dashed-dotted line),

(d) quadratic error indicators ε

c,a

(continuous line), ε

c, f

(dashed line) and ε

a, f

(dashed-dotted line), (e) error in-

dicators ε

c,a

(continuous line), ε

c, f

(dashed line) and ε

a, f

(dashed-dotted line), measured on 2006.

der to reach these objectives. The technique of super-

vision which is presented in this article is based on

the Pattern recognition AUDyC algorithm. It has the

advantage to limit physical knowledge of the system,

and aims to modelling the operating modes of dynam-

ical systems using only measured data. The charac-

teristics of the operating mode are updated in real-

time in order to follow the drifts due to sensor faults,

and detect setting errors and measurement or trans-

mission errors. The proposed technique is applied on

a real hydrographical system with presents the partic-

ularities to not being modelled according to classical

modelling methods. Fault indicators are determined

according to levels which are measured since 2006.

The ﬁrst obtained results highlight the efﬁciency of

the proposed fault detection method. However, these

results have to be improved. The futur purposes con-

sist in proposing more pertinent fault indicators by

considering the measured upstream and downstream

in the Cuinchy-Fontinettes channel. It should be also

interesting to take into account the unknown inputs

which correspond to overﬂows in the channel. In fu-

ture works, a prognosis approach will be proposed to

predict the future state of the level sensors in order to

detect as soon as possible sensor faults. Finally, an

implementation of the proposed technique on the real

system may be considered at term.

REFERENCES

Akhenak, A., Chadli, M., Ragot, J., and Maquin, D. (2004).

State estimation of uncertain multiple model with un-

known inputs. In 43rd IEEE Conference on Decision

and Control, Atlantis, Bahamas, page 35633568.

Bedjaoui, N. and Weyer, E. (2010). Algorithms for leak de-

tection, estimation, isolation and localization in open

water channels. Control Engineering Practice, In

Press.

Chow, V. T., Maidment, D. R., and Mays, L. W. (1998).

Applied Hydrology. McGraw-Hill.

Eltoft, T. and de Figueiredo, R. (1998). A nez neural net-

work for cluster-detection-and-labeling. IEEE Trans.

Neural Networks, 9:1021–1035.

Frank, P. M., Ding, S. X., and KCipper-Seligcr, B. (2000).

Current developments in the theory of fdi. In SAFE-

PROCESS00, Budapest, Hungary, pages 16–27.

Gertler, J. (1998). Fault Detection and Diagnosis in Engi-

neering Systems. Dekker.

Hartert, L., Mouchaweh, M. S., and Billaudel, P. (2010).

Intelligent Industrial Systems: Modeling, Automation

and Adaptive Behavior. IGI.

Lecoeuche, S., Lurette, C., and Lalot, S. (2004). New su-

pervision architecture based on on-line modeling of

non-stationary data. Neural Computing and Applica-

tions Journal, 13:323–338.

Mouchaweh, M. S., Devillez, A., Lecolier, G., and Bil-

laudel, P. (2002). Recursive learning in real time using

fuzzy pattern matching. Mathematics and Computers

in Simulation, 60:209–216.

Su, M.-C. and Liu, Y.-C. (2005). A new approach to clus-

tering data with arbitrary shapes. Pattern Recognition,

38:1887–1901.

Traore, M., Duviella, E., and Lecoeuche, S. (2009). Dy-

namical clustering technique to estimate the proba-

bility of the failure occurrence of process subjected

to slow degradation. In ICINCO, Milan, Italy, pages

636–643.

Weihua, L., Harigopal, R., and Sirish, S. (2003). Subspace

identiﬁcation of continuous time models for process

fault detection and isolation. Journal of Process Con-

trol, 13:407–421.

Xie, L., Soh, Y. C., and de Souzi, C. E. (1994). Ro-

bust kalman ﬁltering for uncertain discrete-time sys-

tems. IEEE Transaction on Automatic Control, 93:131

01314.

SENSOR FAULT DETECTION IN A REAL HYDRAULIC SYSTEM USING A CLASSIFICATION APPROACH

387