OPTIMIZED STRATEGIES FOR ARCHIVING
MULTI-DIMENSIONAL PROCESS DATA
Building a Fault-diagnosis Database
Sebastian Feller
1
, Yavor Todorov
1
, Dirk Pauli
1
and Folker Beck
2
1
FCE Frankfurt Consulting Engineers GmbH, Frankfurter Strasse 5, 65239 Hochheim/Main, Germany
2
John Deere Werke Zweibruecken, Homburger Strasse 117, 66482 Zweibruecken, Germany
Keywords:
Data compression, Time series analysis, Condition based maintenance.
Abstract:
In many real-world applications such as condition monitoring of technical facilities or vehicles the amount
of data to process and analyze has steadily increased during the last decades. In this paper a novel approach
to data compression is presented, namely the multivariate representative of the Perceptually Important Points
algorithm. Furthermore, approaches are given on how multivariate data should be dealt with to preserve all
relevant multivariate information during a lossy data compression. This involves an extensive analysis of the
stochastic dependencies of the process data. On the one hand the presented algorithm is able to compress the
multivariate time series and on the other hand the algorithm can be easily extended to reflect a model of the
original time series. It is shown that suggested multivariate compression algorithm outperforms its univariate
equivalent.
1 INTRODUCTION
The digitalization of sensor equipment and the inte-
gration of these sensors into communication networks
have immensely increased the amount of data avail-
able for various kinds of processes. For utility compa-
nies these large data streams are of particular concern.
For example, as a regulated industry, the power indus-
tries in most western countries are obliged to collect
extensive information on their power production pro-
cesses. Emissions and a diverse number of thermo-
dynamical and mechanical process variables are usu-
ally collected at a rate of one value set per second.
Since modern power plants can have value sets with
over 5000 different readings, a direct evaluation of
this incoming data flood is not possible, and data com-
pression and organization methods become urgent. In
general data compression is of interest, if the quantity
of collected data is too large for given performance in
terms of processing time and storage.
This paper gives a summary of state-of-the-art al-
gorithms used in modern data historians in section
2 and demonstrates their shortcomings considering
the requirements of typical condition monitoring soft-
ware and methods of empirical fault analysis on the
example of ’Perceptually Important Points’. In sec-
tion 4 a first simple example is given. In the following
two section datasets with a more complex structure
are studied under the same premise. Based on these
considerations an improved procedure for multivari-
ate time series compression is suggested in section 7.
2 PROBLEM DESCRIPTION
The initial situation of how data is collected and what
it is used for varies greatly from industry to industry.
In the following the focus is put on the power produc-
ing industry since companies in this industry already
have extensive sensory equipment installed and ex-
hibit capabilities of collecting data in central nodes in
each of their power plants. This is partially due to the
aforementioned regulations enforced on these utility
companies.
A primary purpose for data collection is of course
to control the power plant based on this information.
Additionally some form of data processing and stor-
age will be used. In the most basic variation of data
processing all incoming data is stored on a digital
storage device which is archived when it is full. This
usually fulfills regulation requirements, but valuable
information is lost.
With typical computational power steadily in-
388
Feller S., Todorov Y., Pauli D. and Beck F..
OPTIMIZED STRATEGIES FOR ARCHIVING MULTI-DIMENSIONAL PROCESS DATA - Building a Fault-diagnosis Database.
DOI: 10.5220/0003571803880393
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 388-393
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

creasing and becoming ever more affordable at the
same time, new plausible paths open up. The col-
lected data can be used to feed condition monitor soft-
ware (e.g. refer to (Chevalier et al., 2009)) which
is a key factor to reducing risks, as emerging dam-
ages can be detected long before they become serious
threats. These potentials are frequently recognized by
the operator of the equipment. Unfortunately the sta-
tistical and physical knowledge to process the data is
not always present in the concerning IT departments.
A variety of ’Off-the-Shelf’ data historians are avail-
able which assist the data collection process, but the
implemented algorithms are usually only designed to
quickly store away data and do not incorporate con-
cerns about advanced data evaluation techniques, e.g.
condition monitoring with anomaly detection algo-
rithms, such as Auto-Associative Kernel Regression,
refer to (Chevalier et al., 2009).
A survey of the current state-of-the-art time se-
ries data compression algorithms, such as Swinging-
Door-Compression, e.g. refer to (Fu, 2010), (Thorn-
hill et al., 2004), (Bristol, 1990), and Perceptually-
Important-Points (PIP), e.g. refer to (Fu, 2010),
(Chung et al., 2001), (Fu et al., 2001), or compres-
sion based on Fast-Fourier-Transformation, e.g. re-
fer to (Fu, 2010), (Stoffer, 1999), (Press et al., 2007),
Wavelet-Transformations, e.g. refer to (Fu, 2010),
(Chen et al., 2004), (Press et al., 2007), or Cheby-
shev polynomials (Hawkins III et al., 2003), (Eruhi-
mov et al., 2008), shows that current techniques fo-
cus on univariate compression. These approaches ne-
glect any correlations between different sensor read-
ings which lead to a suboptimal compression of the
process data as shown in the remaining paper.
3 NOVEL APPROACH ON
MULTIVARIATE DATA
COMPRESSION
The current paper concentrates on the development of
a multivariate variant of the PIP algorithm. Hence, its
univariate representative is introduced first.
The aim of the algorithm can be summarized
as approximating historical time series T = {x
i
} by
piecewise linear functions, where i ∈ {1, ...,n} is the
time index. The result is a set P of the so called per-
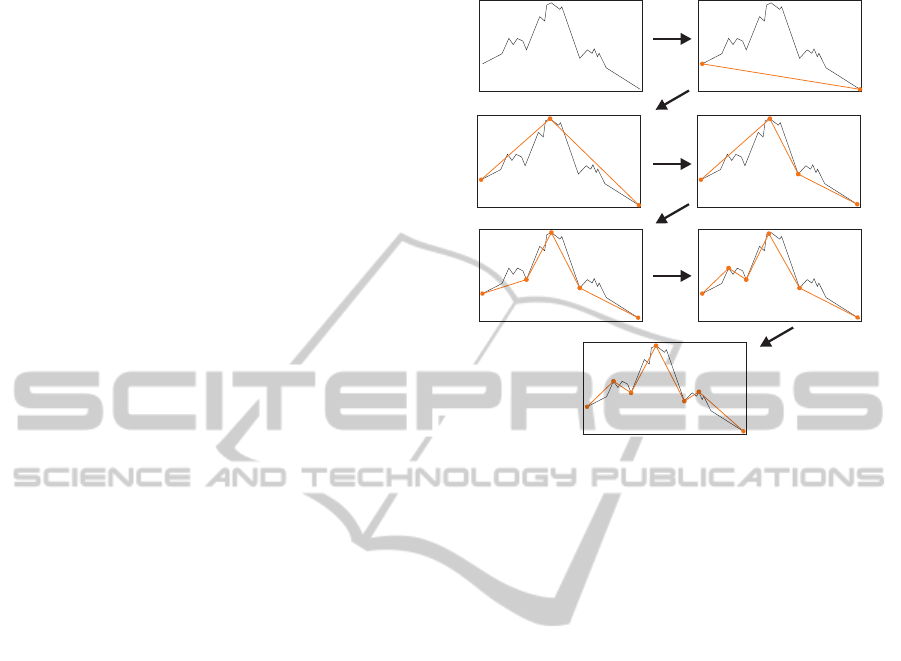
ceptually important points. Figure 1 gives an example
of an approximation. Note that linear functions are
defined by two sequent perceptually important points.
The algorithm is initialized with P = {x
1
,x
n
}, re-
fer to figure 1. Following, the next ’important’ point
of T/P is determined via its Euclidian distance to
‚PIP‘-Algorithm
Figure 1: Example of incrementally estimated PIP. The first
and last element of the time series are used for initializa-
tion, following ’important’ points are determined via their
distance to the corresponding linear function.
its corresponding approximation. As shown in fig-
ure 1, adding points to P changes the approximation
of T. The procedure of determining the next ’impor-
tant’ point terminates, if a criteria for convergence is
fulfilled. This can be a certain compression ratio or
a global mean squared error, to name a few possible
criteria.
In the following, the univariate PIP compression
algorithm is extended to its multivariate representa-
tive. This influences the estimation of the next ’im-
portant’ point as well as performance requirements or
convergence criteria. As with the univariate represen-
tative the first and last point of the time series are used
for initialization. Figure 2 depicts a typical situation
during the approximation procedure. The points at
times 0, 1 and n already have been selected. The in-
dex τ
∗
of the next point added to the approximation is
identified via
τ
∗
= argmax
τ∈{0,...,n}
kp(τ) − p
∗
(τ)k,
where p
∗
(t) is the linear approximation of the point
p(t) given the current selection of PIPs.
4 AN INTRODUCTORY
EXAMPLE
Beginning with artificial data, statistical properties of
OPTIMIZED STRATEGIES FOR ARCHIVING MULTI-DIMENSIONAL PROCESS DATA - Building a Fault-diagnosis
Database
389

p(t=0)
x
y
t
p(t=n)
x
y
p(t=1)
x
y
p(t=t)
x
y
d
t
p*(t= )t
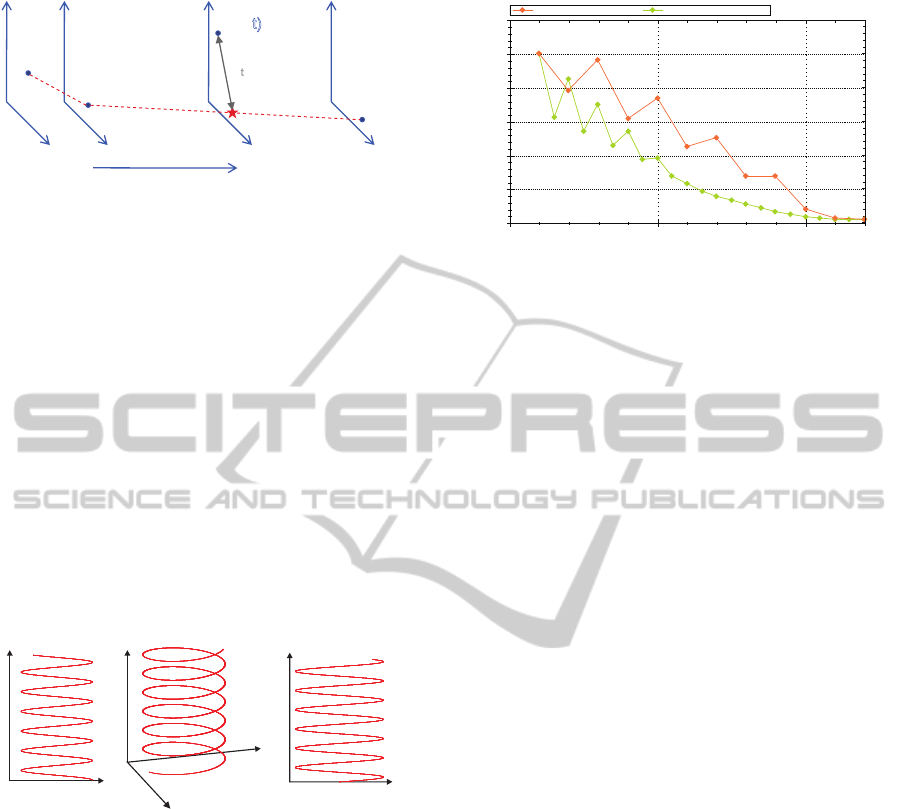
Figure 2: Snapshot of the approximation procedure of the
multivariate PIPs. The first and last elements of the time se-
ries are used for initialization. The following points are de-
termined via their Euclidian distance d
τ
to the correspond-
ing linear approximation.
the univariate and multivariate compression algo-
rithms are compared. A test on artificial data is shown
in figure 3 and 4. The compression algorithm used in
this example is a univariate and multivariate percep-
tual importance algorithm, e.g. compare (Fu, 2010),
(Chung et al., 2001), and (Fu et al., 2001). Consid-
ering the two dimensional goodness of fit, measured
by the mean squared error (fig. 4), it can be seen
that the multivariate algorithm outperforms the uni-
variate equivalent. To understand this, one has to bear
in mind that compressing a two dimensional or any
higher dimensional time series in a univariate fashion
generally results in PIPs not being aligned in the time
domain. This can lead to an inferior compression.
t
x
y
y
t
y(t) = cos(t)
f (t) = (x,y) = (sin(t), cos(t))
T T
x
t
x(t) = sin(t)
Figure 3: Two dimensional time series consisting of a sine
and cosine dependent on a parameter t with equal phase,
frequency and amplitude. The result in two dimensional
space is a helix.
5 COMPRESSION RATIO VS.
COMPRESSION QUALITY
The analysis of the multivariate PIP algorithm is con-
tinued by considering three artificial datasets. The
artificial datasets are chosen so that the statistical
properties, especially in terms of stochastic depen-
dence, are fully established. The first dataset con-
sists of ten independent Ornstein-Uhlenbeck pro-
cesses (Gillespie, 1996) and (Uhlenbeck and Orn-
stein, 1930) each given by the equation:
dX
t
= θ(µ− X
t
)dt + σdW
t
,
0 10 20
Number of Approximation Points
0,0
0,1
0,2
0,3
0,4
0,5
0,6
M
ean Squared Error of Approximation
Univariate Compression Multivariate Compression
Figure 4: Comparison between univariate (orange line) and
multivariate (green line) compression of the artificial data
shown in figure 3. The figure shows the mean squared ap-
proximation error versus the number of points used to ap-
proximate the helix. In this case the multivariate algorithm
outperforms the univariate equivalent.
where dW
t
is the increment of a Wiener process. The
processes are initialized by random values distributed
according to X
0
∼ N (0,σ
2
). Ornstein-Uhlenbeck
processes are chosen since they closely resemble the
dynamics of a real system (Feller, 2009). The two
additional datasets are also generated via Ornstein-
Uhlenbeck processes. In case of the second and third
dataset the processes are not independent any more.
A correlation is introduced by a system of differential
equations that drive the underlying dynamics of the
observed process and a observer equation. The sys-
tem of differential equations is in the form of
d
~
X
t
= Θ(~µ− Ψ
~
X
t
)dt + σ
X
d
~
W
t
,
where Ψ is a symmetrical matrix and Θ is a diago-
nal matrix with the elements θ
i
. For the first dataset
Ψ is an identity matrix. For the second example Ψ
has block diagonal structure and for the third random
correlations are chosen on initialization. The observer
equation is given by
~
Y
t
= A·
~
X
t
+ σ
Y
d
~
W
t
,
where
~
Y
t
is the observed signal vector. For the first
dataset
~
Y
t
≡
~
X
t
. For the second dataset
~
X
t
has 6 and
for the third 2 dimensions. The dimension of
~
Y
t
is al-
ways 10. The dimensions of A vary correspondingly.
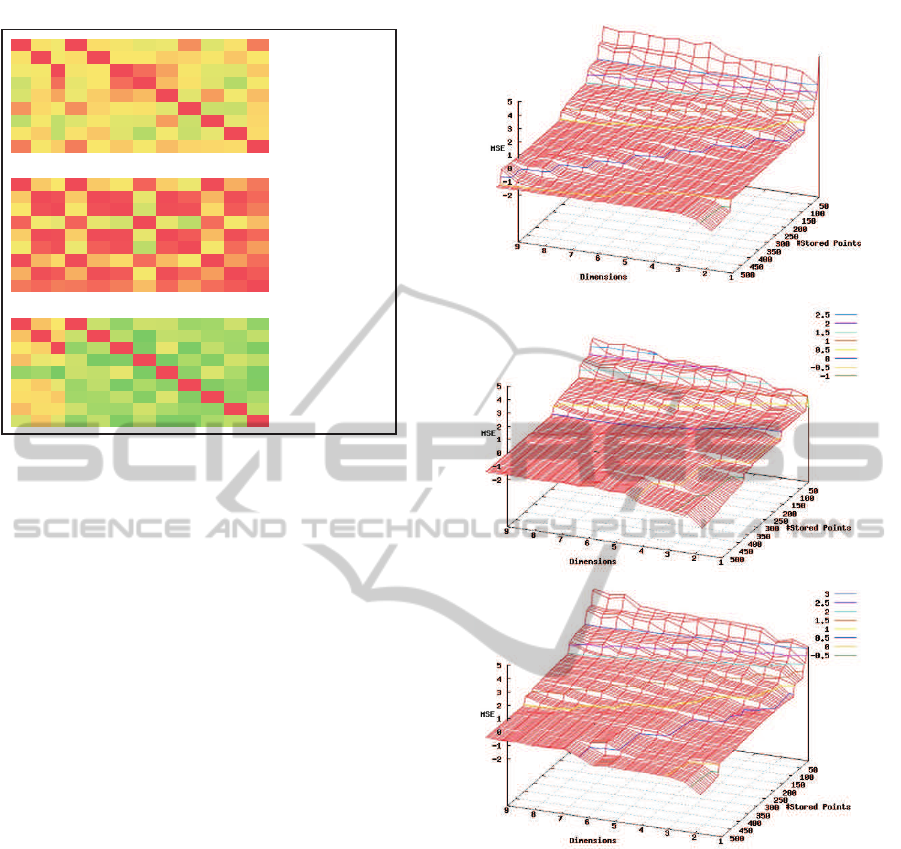
Figure 5 shows an example for the non-linear correla-
tion between the parameters of each dataset type. The
correlations were calculated from one sample. In this
figure green colors depict a low correlation and red
colors stand for a high correlation.
In figure 6 the compression results for the three
datasets are shown. In the graphs the logarithm of
MSE is shown versus the number of dimensions com-
pressed and the number of PIPs selected for linear
approximation. In order to smooth out any random
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
390

1,0 0,7 0,6 0,5 0,6 0,9 0,5 0,7 0,9
0,7 1,0 0,7 0,7 0,7 0,7 0,7 0,7 0,7
0,6 0,7 1,0 0,9 0,8 0,7 0,5 0,5 0,7
0,5 0,7 0,9 1,0 0,8 0,7 0,5 0,3 0,6
0,6 0,7 0,8 0,8 1,0 0,5 0,8 0,6 0,8
0,9 0,7 0,7 0,7 0,5 1,0 0,4 0,4 0,7
0,5 0,7 0,5 0,5 0,8 0,4 1,0 0,5 0,7
0,7 0,7 0,5 0,3 0,6 0,4 0,5 1,0 0,7
0,9 0,7 0,7 0,6 0,8 0,7 0,7 0,7 1,0
1,0 0,7 0,7 1,0 0,7 0,6 1,0 0,8 0,9
Dependent
0,7 1,0 1,0 0,5 1,0 1,0 0,8 1,0 0,9
0,7 1,0 1,0 0,4 1,0 1,0 0,7 1,0 0,9
1,0 0,5 0,4 1,0 0,5 0,3 0,9 0,6 0,8
0,7 1,0 1,0 0,5 1,0 1,0 0,8 1,0 0,9
0,6 1,0 1,0 0,3 1,0 1,0 0,6 0,9 0,8
1,0 0,8 0,7 0,9 0,8 0,6 1,0 0,8 0,9
0,8 1,0 1,0 0,6 1,0 0,9 0,8 1,0 1,0
0,9 0,9 0,9 0,8 0,9 0,8 0,9 1,0 1,0
1,0 0,4 0,1 0,4 -0,4 0,2 0,2 0,4 -0,1
Independent
0,4 1,0 0,3 0,0 -0,3 0,3 0,2 0,2 0,3
0,1 0,3 1,0 0,0 -0,5 0,0 0,3 0,2 0,0
0,4 0,0 0,0 1,0 0,0 0,2 0,1 0,4 -0,3
-0,4 -0,3 -0,5 0,0 1,0 0,1 -0,5 -0,2 0,0
0,2 0,3 0,0 0,2 0,1 1,0 0,0 -0,1 0,0
0,2 0,2 0,3 0,1 -0,5 0,0 1,0 0,1 0,2
0,4 0,2 0,2 0,4 -0,2 -0,1 0,1 1,0 -0,3
-0,1 0,3 0,0 -0,3 0,0 0,0 0,2 -0,3 1,0
1,0 0,7 0,6 0,5 0,6 0,9 0,5 0,7 0,9 SemiDependent
0,7 1,0 0,7 0,7 0,7 0,7 0,7 0,7 0,7
0,6 0,7 1,0 0,9 0,8 0,7 0,5 0,5 0,7
0,5 0,7 0,9 1,0 0,8 0,7 0,5 0,3 0,6
0,6 0,7 0,8 0,8 1,0 0,5 0,8 0,6 0,8
0,9 0,7 0,7 0,7 0,5 1,0 0,4 0,4 0,7
0,5 0,7 0,5 0,5 0,8 0,4 1,0 0,5 0,7
0,7 0,7 0,5 0,3 0,6 0,4 0,5 1,0 0,7
0,9 0,7 0,7 0,6 0,8 0,7 0,7 0,7 1,0
1,0 0,7 0,7 1,0 0,7 0,6 1,0 0,8 0,9
Dependent
0,7 1,0 1,0 0,5 1,0 1,0 0,8 1,0 0,9
0,7 1,0 1,0 0,4 1,0 1,0 0,7 1,0 0,9
1,0 0,5 0,4 1,0 0,5 0,3 0,9 0,6 0,8
0,7 1,0 1,0 0,5 1,0 1,0 0,8 1,0 0,9
0,6 1,0 1,0 0,3 1,0 1,0 0,6 0,9 0,8
1,0 0,8 0,7 0,9 0,8 0,6 1,0 0,8 0,9
0,8 1,0 1,0 0,6 1,0 0,9 0,8 1,0 1,0
0,9 0,9 0,9 0,8 0,9 0,8 0,9 1,0 1,0
1,0 0,4 0,1 0,4 0,4 0,2 0,2 0,4 0,1
Independent
0,4 1,0 0,3 0,0 0,3 0,3 0,2 0,2 0,3
0,1 0,3 1,0 0,0 0,5 0,0 0,3 0,2 0,0
0,4 0,0 0,0 1,0 0,0 0,2 0,1 0,4 0,3
0,4 0,3 0,5 0,0 1,0 0,1 0,5 0,2 0,0
0,2 0,3 0,0 0,2 0,1 1,0 0,0 0,1 0,0
0,2 0,2 0,3 0,1 0,5 0,0 1,0 0,1 0,2
0,4 0,2 0,2 0,4 0,2 0,1 0,1 1,0 0,3
0,1 0,3 0,0 0,3 0,0 0,0 0,2 0,3 1,0
Figure 5: Examples for the Spearman rank correlation for
each of the designed datasets shown in a correlation matrix.
Green colors depict a low correlation and red colors stand
for a high correlation between the parameter pairs.
effect the analysis was repeated with 100 different
datasets each.
The results for the compression of one dimension
is similar for all datasets.
From figure 6 it can be seen, that with increasing
dimensions the amount of PIPs required to achieve
the same goodness of fit is exponentially larger in the
case of the independent processes.
6 CONDITION MONITORING
CASE STUDY ON TWO REAL
DATASETS
Considering datasets from real systems it is important
to keep the findings of the previous section in mind.
It is crucial only to compress multivariate datasets if
the individual signals have significant stochastic de-
pendencies with each other. In case these stochas-
tic dependencies do not exist, it is possible to iso-
late groups of highly dependent signals. In this man-
ner a dataset can be split into a number of subset
datasets which each contain the required amount of
data. These groups of dependent signals are also very
beneficial for the application of a condition monitor-
ing software (Feller and Chevalier, 2010).
The multivariate extension of the perceptually im-
portant points algorithm was applied to two case study
datasets. The first dataset originates from a gas tur-
bine and the second comes from an agricultural ve-
hicle. The dataset from the gas turbine consists of
SemiDependent
Dependent
Independent
Figure 6: The three graphs show the logarithm of MSE ver-
sus the number of dimensions compressed and the number
of PIPs selected for linear approximation. The top most
graph results from the compression of the artificial dataset
2 which has a medium dependency between different di-
mensions. The center graph results from the third artifi-
cial dataset. Finally the bottom graph results from the first
dataset with the lowest dependency. The colored lines in
each graph depict levels of equal goodness of fit. For each
graph the same scales and view were used. To smooth out
any random effects the analysis was repeated 100 times and
the results were averaged.
5000 samples, each containing 120 different param-
eters. The parameters include mechanical and ther-
modynamical variables. The dataset from the agricul-
tural vehicle contains 3750 samples, each with 130
different parameters. The parameters primarily con-
tain mechanical variables, such as vibrations. Fig-
ure 8 summarizes the compression progress for both
OPTIMIZED STRATEGIES FOR ARCHIVING MULTI-DIMENSIONAL PROCESS DATA - Building a Fault-diagnosis
Database
391

datasets. The figure shows the mean squared error
as well as the maximum error. The maximum error
is simply the largest Euclidean distance between the
current approximation and any point. Both datasets
can be approximated very well with the PIP algo-
rithm, even at high compression ratios.
Figure 7 shows the application of the multivari-
ate PIP algorithm in combination with a data driven
condition monitoring algorithm. The algorithm used
is based on an autoassociative kernel regression
(AAKR) algorithm (Hines and Garvey, 2006). For
evaluation purposes the original datasets were split
into two equally large sets. The first part served as
training for the data driven algorithm and was com-
pressed via PIP previous to training. The second part
of the dataset was used as validation for the anomaly
detection. Figure 8 was derived from the first halves
and figure 7 was derived from the second halves of
the datasets.
Gas Turbine
Agricultural Vehicle
500 600 700 800 900 1000 1100 1200 1300 1400
# PIPs
0
100
200
300
400
500
600
700
MSE (10^-6)
0,00
0,01
0,02
0,03
0,04
Anomaly Detection MSE vs. #PIPs
Anomaly Detection Max Error vs. #PIPs
Max Error
600 800 1000 1200 1400 1600 1800
# PIPs
0
1000
2000
3000
4000
5000
6000
7000
0,0
0,5
1,0
1,5
2,0
Max Error
Anomaly Detection MSE vs. #PIPs
Anomaly Detection Max Error vs. #PIPs
MSE (10^
-6)
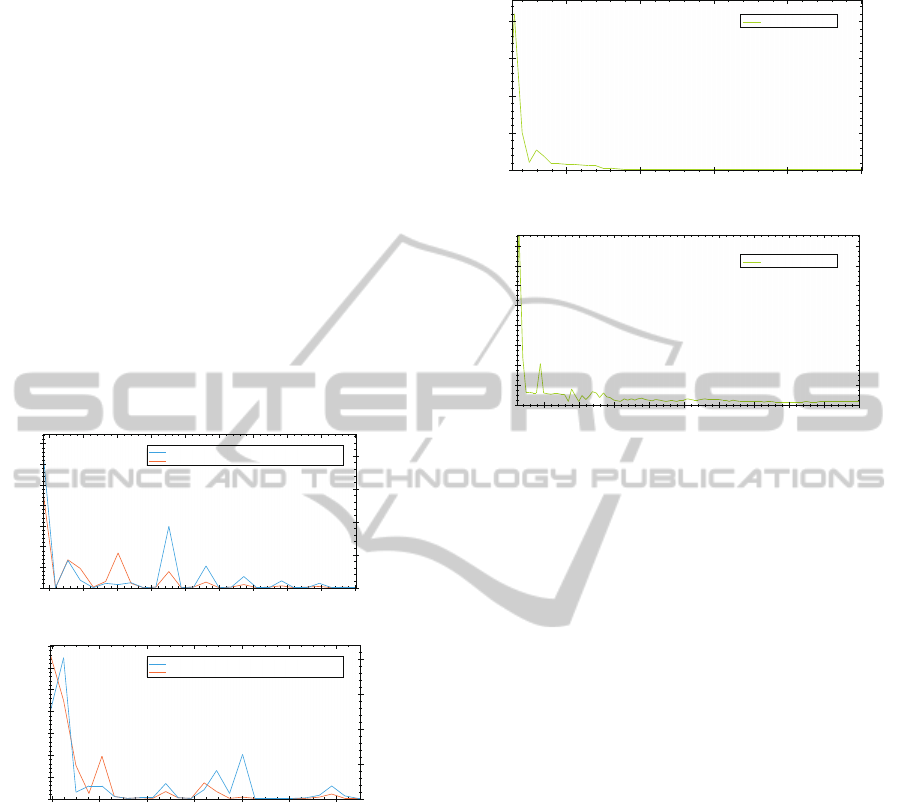
Figure 7: The two graphs show the mean squared error
(MSE) as well as the maximum error for anomaly detection
on the validation set for each dataset versus the number of
PIPs used. The original datasets were split into two halves.
The first halves were compressed via the multivariate PIP
algorithm and then used as training data for the AAKR al-
gorithm. The second halves of the original datasets, called
validation sets, were then evaluated with the trained AAKR
algorithms. For the agricultural vehicle both error types
quickly drop to very low levels. This suggests that the train-
ing contains only few different states. A compression ratio
of 1 : 4 seems as an acceptable choice for this type of sys-
tem. The gas turbine shows a similar behavior. Here a com-
pression ratio of 1 : 3 seems to be an adequate choice.
7 FURTHER CONSIDERATIONS
In the previous section a lossy compression of mult-
10 20 30 40 50 60 70 80 90 100
# PIPs
0
200
400
600
800
1000
1200
1400
1600
MSE
Error vs. #PIPs
Gas Turbine
Agricultural Vehicle
10 20 30 40 50
0
100
200
300
400
MSE
# PIPs
Error vs. #PIPs
Figure 8: The two graphs show the mean squared error
(MSE) of compression versus the number of PIPs selected
by the algorithm for the two training sets. The original
datasets were split into two halves. The first halves were
compressed via the multivariate PIP algorithm and the used
as training data for the AAKR algorithm. The second halves
of the original datasets, called validation sets, were then
evaluated with the trained AAKR algorithms. For the first
training set (agricultural vehicle) and the second training
set (gas turbine) the approximation error quickly converges
to zero. This suggest that both datasets are well suited for
compression through a multivariate compression algorithm.
ivariate datasets using the perceptually important
points algorithm was considered. As this algorithm
contains no optimization in terms of preserving sta-
tistical properties such as mean and variance of the
original dataset, additional steps have to be taken to
preserve these. Information about the multivariate
statistics can be preserved e.g. by combining the
lossy compression with a kernel density estimation
(Jones et al., 1996) technique. In this configuration
the dataset is compressed first through the PIP algo-
rithm. In a second step a kernel density estimation
(KDE) with the selected PIP utilized as centers for
the kernels is applied. The kernel parameters are then
adjusted to fit the original dataset. In a decompression
stage the likelihood for the current state being in each
PIP is calculated and stochastic properties are simu-
lated through the weighted density estimation.
With this procedure the compression reflects a
model of the original time series. It can be ensured
that relevant statistical properties of the process data
are not lost during compression, although the exact
occurrence of the original dataset is lost. The com-
bination of these two approximation algorithms con-
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
392

serves the time dependencies as well as statistical
properties of the original process.
8 CONCLUSIONS
It was shown that datasets exhibiting strong stochas-
tic dependencies can be efficiently compressed by a
multivariate compression algorithm. On the example
of a simple artificial dataset it was demonstrated that
especially in the domain of high compression ratios
the multivariate compression algorithm outperforms
its univariate equivalent.
In extension to condition monitoring, utility com-
panies are beginning to build fault diagnosis data
bases to diagnose upcoming critical events through
empirical fault diagnostic algorithms, refer to (Feller
et al., 2010). These efforts require optimized long-
term compression techniques which are able to sep-
arate relevant from non relevant information in high
dimensional process data. The introduced multivari-
ate compression algorithm is able to provide the nec-
essary features.
REFERENCES
Bristol, E. (1990). Swinging door trending: Adaptive trend
recording. In ISA National Conference Proceedings,
volume 45, pages 749–753.
Chen, H., Li, J., and Mohapatra, P. (2004). RACE: Time se-
ries compression with rate adaptivity and error bound
for sensor networks. In Mobile Ad-hoc and Sen-
sor Systems, 2004 IEEE International Conference on,
pages 124–133. IEEE.
Chevalier, R., Provost, D., and Seraoui, R. (2009). As-
sessment of Statistical and Classification Models For
Monitoring EDFs Assets. In Sixth American Nu-
clear Society International Topical Meeting on Nu-
clear Plant Instrumentation.
Chung, F., Fu, T., Luk, R., and Ng, V. (2001). Flexible time
series pattern matching based on perceptually impor-
tant points. In International Joint Conference on Ar-
tificial Intelligence Workshop on Learning from Tem-
poral and Spatial Data, pages 1–7.
Eruhimov, V., Martyanov, V., Raulefs, P., and Tuv, E.
(2008). Supervised compression of multivariate time
series data. Relation, 10(1.125):5395.
Feller, S. (2009). Parameteridentifikation bei einem
geregelten multidimensionalen stochastischen prozess
am beispiel einer reaktorkhlpumpe. Diplomarbeit.
Feller, S. and Chevalier, R. (2010). Parameter Disaggre-
gation for High Dimensional Time Series Data on the
Example of a Gas Turbine. In 38th ESReDA Seminar,
Pcs, Hungary, May 4-5, 2010.
Feller, S., Chevalier, R., Paul, N., and Pauli, D. (2010).
Classification Methods for Failure Mode Diagnosis on
the Example of Synthetic Data and RCP Leak Flow
Data. In EPRI Technical Report.
Fu, T. (2010). A review on time series data mining. Engi-
neering Applications of Artificial Intelligence, pages
164–181.
Fu, T., Chung, F., Ng, V., and Luk, R. (2001). Pattern
discovery from stock time series using self-organizing
maps. In The 7th ACM SIGKDD International Con-
ference on Knowledge Discovery and Data Mining,
Workshop on Temporal Data Mining, pages 26–29.
Citeseer.
Gillespie, D. T. (1996). Exact numerical simulation of the
ornstein-uhlenbeck process and its integral. Phys. Rev.
E, 54(2):2084–2091.
Hawkins III, S., Darlington, E., Cheng, A., and Hayes, J.
(2003). A new compression algorithm for spectral and
time-series data. Acta Astronautica, 52(2-6):487–492.
Hines, J. W. and Garvey, D. R. (2006). Development
and Application of Fault Detectability Performance
Metrics for Instrument Calibration Verification and
Anomaly Detection. Journal of Pattern Recognition
Research, 1(1).
Jones, M. C., Marron, J. S., and Sheather, S. J. (1996). A
brief survey of bandwidth selection for density estima-
tion. Journal of the American Statistical Association,
91:401–407.
Press, W., Teukolsky, S., Vetterling, W., and Flannery, B.
(2007). Numerical Recipes: The Art of Scientific Com-
puting. Cambridge University Press.
Stoffer, D. (1999). Detecting Common Signals in Multiple
Time Series Using the Spectral Envelope. Journal of
the American Statistical Association, 94(448).
Thornhill, N., Shoukat Choudhury, M., and Shah, S. (2004).
The impact of compression on data-driven process
analyses. Journal of Process Control, 14(4):389–398.
Uhlenbeck, G. E. and Ornstein, L. S. (1930). On the theory
of the brownian motion. Phys. Rev., 36(5):823–841.
OPTIMIZED STRATEGIES FOR ARCHIVING MULTI-DIMENSIONAL PROCESS DATA - Building a Fault-diagnosis
Database
393