VEHICLE ROUTING PROBLEM WITH MULTI-DEPOT

AND MULTI-TASK

Haoxiong Yang, Li Jing

School of Business, Beijing Technology and Business University, No.33 Fucheng Road, Beijing, China

Yongsheng Zhou, Mingke He

Department of Logistics Management, Beijing Technology and Business University, Beijing, China

Keywords: City distribution, Multi-depot, Multi-task, Vehicle routing problem, Self-adaptive, Polymorphic ant colony

algorithm (APACA).

Abstract: This paper presents a new mathematical model of the vehicle routing problem in the context of city

distribution, which considers multi-depot, multi-model vehicles and multi-task. The objective function

includes three parts: transport cost, deadheading cost and time cost. To solve this mathematical model, a

self-adaptive and polymorphic ant colony algorithm (APACA) has been introduced. Finally, a case study is

presented to compare the results based on APACA with that under stochastic condition. Simulation results

show that APACA is an effective and desirable algorithm for solving the mathematical model.

1 INTRODUCTION

Vehicle routing problem (VRP) is an important part

of city distribution activities. The optimization for

the vehicle routing problem contributes to improve

the efficiency of goods distribution, reduce total

distribution cost and increase customer satisfaction.

Take Keihanshin metropolitan region in Japan for

example, since the optimization strategy was taken

by local government in 1989, the next surveys

shown that average number of transport vehicles had

been reduced by 17%, total deliver time had been

reduced by 89%, and total travel distance had been

reduced by 72%.

In the context of city distribution, vehicle routing

problem has the following features: multi-depot,

multi-model vehicles and multi-task. These features

make vehicle routing problem more complicated

than that under the condition of single-depot, single-

model vehicle and single-task, but practical

significance. In previous studies, Koehler (1999)

described Kassel joint distribution system, and

pointed that this system can decrease total travel

time and the number of transport vehicles obviously;

T Yamada et al. (2001) proposed a decisive model

of co-operative vehicle routing, and analyzed the

impact of co-distribution center location on deliver

effectiveness; Renaud et al. proposed different

branch-and-bound algorithms for symmetrical multi-

depot vehicle routing problem and asymmetrical

multi-depot vehicle routing problem. Yaohuang Guo

(1995) and Shengce Hang et al. (1997) firstly

transformed multi-depot vehicle routing problem

into single-depot problem and then applied the

method for solving single-depot problem into multi-

depot problem; Mingshan Zhang (2002) discussed a

general distributing route problem under the

condition of multi-depot and full-load and proposed

a heuristic algorithm for optimizing distributing

route based on network flow model.

Take a broad view of previous studies, the

majority of the studies have been of help to

enterprises or governments; however for most of

them the following aspects can be improved in the

following aspects:

 More constraints such as multi-depot, multi-

model vehicles, multi-task and capacity should be

considered together, rather than only one or two

constraints;

 The target of mathematical model is not only to

minimize travel distance or cost in part distribution

activities but also to minimize total travel cost in all

650

Yang H., Jing L., Zhou Y. and He M..

VEHICLE ROUTING PROBLEM WITH MULTI-DEPOT AND MULTI-TASK.

DOI: 10.5220/0003573406500655

In Proceedings of the 13th International Conference on Enterprise Information Systems (MMLM-2011), pages 650-655

ISBN: 978-989-8425-56-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

distribution processes.

Since the vehicle routing problem in the context of

city distribution is a complex system in which

constraints including multi-depot, multi-model

vehicles and multi-task are often occurred and the

target to minimize total travel cost (includes

transport cost, deadheading cost and time cost) is

more meaningful than the target to minimize travel

distance. As a result, the previous studies are not

fully based on actual situations in the context of city

distribution.

Based on the above studies, we first describe a

practical city distribution problem whose constraints

involve multi-depot, multi-model vehicles and

multi-task, and establish its mathematical model

whose objective function includes three parts:

transport cost. Then, we state the design of an self-

adaptive and polymorphic ant colony algorithm

(APACA) for solving the problem. Finally the

computational results of the actual instance show the

effectiveness of the proposed method.

2 THE VEHICLE ROUTING

PROBLEM WITH

MULTI-DEPOT,

MULTI-MODEL VEHICLES

AND MULTI-TASK

2.1 Problem Description

In city distribution system, there are several depots.

Each of them has some different model vehicles.

Different model vehicle has different capacity, unit

transport cost, deadheading cost and unit time cost.

Each vehicle must set out from its depot to

distribution center for carrying goods. Then, the

vehicles deliver goods to all demand points. Each

demand point has a service soft time window which

means that if the arrival time at a demand point is

earlier than the beginning of the time window or

later than the end of the time window, the cost

function will be penalized by some amount. A

demand point is serviced exactly once by only one

vehicle. The problem that we propose is that in order

to minimize total travel cost (includes transport cost,

deadheading cost and time cost) how to decide right

vehicles and chose right distributing routes in the

above circumstances.

2.2 Mathematical Model

Let us consider a routing network which is compo-

sed of depots, distribution center and customer

points. In city distribution activities, the vehicle K

sets out from the depot S to the distribution center O

for loading goods, and then delivers goods to the

customer point N. Finally, the vehicle K needs to

return to its start point, namely depot S. The problem

is defined on a complete graph G(V,A) (shown in

Figure 1), where

V=(v

,…,v

n+1

n+2

n+3

,…,v

n+m+1

) is a vertex set

and E={（v

）: v

, v

∈ V , i ≠ j}is the arc set. V

includes three subsets: N={v

,…,v

} is a customer

vertex set, O={ v

n+1

} is a distribution center vertex

set, S={ v

n+2

n+3

,…,v

n+s+1

} is a depot vertex set. For

each v

∈ N, it includes the demand of the customer;

for each v

∈ S, it includes the number of the vehicle

model; K={1,2,…,k} is a vehicle model vertex set;

each customer v

has a service time window [ET

, LT

]

where

is the earliest time that service can begin

and

is the latest time that service can begin. If the

arrival time at a demand point is earlier than the

beginning of the time window or later than the end

of the time window, the cost function will be

penalized by some amount.

Figure 1: The illustration of the Vehicle Routing.

In order to simplify the problem, we define the

sets, parameters and variables used in the

mathematical model as follows:

 We denote the customers by 1,2,…,N ;

distribution center by N+1; depots by N+2, N+3,…,

N+S+1 and the vehicle models by 1,2,…,K;



=(1,0)：If vehicle k in the depot s travel form

vertex i to vertex j the

=1, otherwise

=0；

 D

: Distance between node i and node j；

VEHICLE ROUTING PROBLEM WITH MULTI-DEPOT AND MULTI-TASK

651

 N: Total number of customers；

 S: Total number of depots；

 C

Unit transportation cost of vehicle k；

 E

Unit deadheading cost of vehicle k；

 V

:Unit travel distance of vehicle k；

 Q

: Capacity of vehicle k；

 W

: Demand at customer i；

 T

: Arrival time at node i；

 t

: Travel time from node i to node j；

 ET

: Earliest arrival time at node i；

 LT

: Latest arrival time at node i；

 A: Earliness penalty coefficient；

 B: Tardiness penalty coefficient

The target of this mathematical model is to minimize

total travel cost (includes transport cost,

deadheading cost and time cost) which is occurred in

the process of city distribution.

The formulation of the problem is as follows:

sk sk sk

ij ij k ij kk

ij ij ij

iONjNsSkKiSjOsSkKiNjssSkK

rD rDE rDE

min

    

   

 









max( , 0 ) max( , 0 )

jj j j

iONjNsSkK

rETT TLT



 

 



(1)

iO Nj N

kKsS









(2)

iO NsSk K











(3)

0, ,

ksk

ij ji

jN jN

kKsS







(4)

1, , ,

iNkKsS





  

(5)

(),

iN OsSkK

rT T





 



(6)

iN OjNsSk K









(7)

S

(8)

The objectives, formula (1) is to minimize the total

vehicle travel cost ((includes transport cost,

deadheading cost and time cost); Formula (2)

constraints the vehicle capacity; Formula (3) ensures

that a customer is serviced exactly once by only one

vehicle; Constraint (4) and (5) guarantee that each

vehicle sets out from the depot and returns to it;

Formula (6) is to compute the arrival time when the

vehicle arrives at customer j; Constraint (7) ensures

that each customer will be serviced; Formula (8)

denotes that the initial time starts form the depot,

and the initial time is equal to zero.

2.3 The Design of Self-adaptive and

Polymorphic Ant Colony

Algorithm (APACA) for Solving

Multi-depot, Multi-model Vehicles

and Multi-task Vehicle Routing

Problem

2.3.1 The Overall Idea of Self-adaptive and

Polymorphic ant Colony Algorithm

(APACA)

The design idea of self-adaptive and polymorphic

ant colony algorithm (APACA) in this paper is as

follows: Based on traditional colony algorithm for

the travelling salesman problem (TSP),we improve

the traditional colony algorithm in information

selective mechanism, information update mechanism

and information collaborative mechanism, and also

introduce self-adaptive migration rule into the

traditional colony. Because the division of labor in

ants is diverse, we allocate the tasks with many

constraints to detective ants. Then, the task to find

feasible solutions of the target function is completed

by searching ants. We combine information self-

adaptive rule and polymorphic ant colony algorithm

perfectly by the collaboration between different

kinds of ants. As a result, self-adaptive and

polymorphic ant colony algorithm (APACA) can

overcome the drawbacks such as long computing

time and precocity which happen in traditional ant

algorithm.

2.3.2 The Steps of Self-adaptive and

Polymorphic Ant Colony Algorithm

(APACA)

The heading of a subsection title should be in 12-

point bold with initial letters capitalized, aligned to

the left with a linespace exactly at 13-point, hanging

indent of 1,0-centimeter and with According to the

principle of self-adaptive and polymorphic ant

colony algorithm (APACA) proposed by Meijun

Chen et al. (2008), we apply this algorithm for

solving multi-depot, multi-model vehicles and multi-

task vehicle routing problem, Specific steps and

methods are as follows:

 Step 1: Initialize Q, C and N

c,max

;

 Step 2: Put n detective ants in n cities, and each

detective ant revolves around city i. Then, the

detective ant detects other n-1 cities. Calculate the

detective table and assign the calculating results to

;

 Step 3: Set the information value of every route

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

652

at initial time;

 Step 4: Set that the initial value of N

is equal to

zero;

 Step 5:Randomly select the initial coordination

of every ant, and put the coordination into its tabu

table;

 Step 6: Calculate the migrating coordination of

every searching ant. Suppose that the migrating

coordination is point j and the last coordination is

point i. Then, put the coordination of point j into

tabu

table of searching ant k. Until each searching

ant visits all coordinations, we can get a solution;

 Step 7: Calculate all solutions of the target

function f(Z

) (k=1,2,…,n), and record all the

solutions;

 Step 8: Lead 2-opt local optimization to all the

above solutions, if new solutions is better than initial

solutions, then we replace initial solutions with new

solutions; Otherwise, we have initial solutions;

 Step 9: If cycle counts comes to N

c,max

, go to

step12. If cycle counts does not come to N

c,max

and

the solution isn’t improved in recent several

iterations, then we should change the value ρ, go to

step 11. Otherwise, go to step 10;

 Step 10: Change the information value of every

route, reset







and clear tabu

table;

 Step 11: N

←N

+1, go to step5;

 Step 12: Output the optimal solution.

3 SIMULATION EXAMPLE

In simulation example, in order to get the optimal

solution, the algorithm is implemented under the

visual studio 2005. The computational experiment

assumed to have three delivery depots, one

distribution center and sixteen customers. All the

nodes are distributed in a 100×100 square region,

each depot has two kinds of model vehicle.

Customer data can be seen in Table 1; Depot and

distribution center data can be seen in Table 2;

Vehicle data can be seen in Table 3.

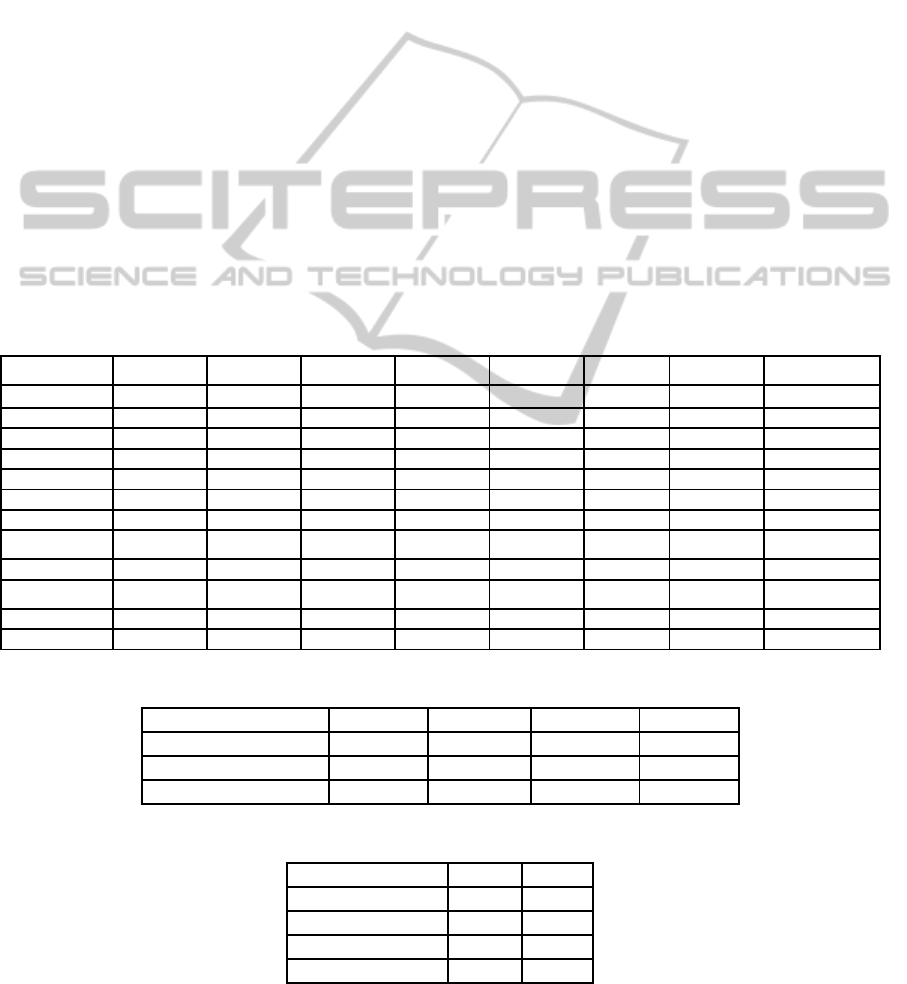
Table 1: Customer data.

Customer 1 2 3 4 5 6 7 8

Coordination

（88,55）（39,31）（20,76）（65,98）（95,23）（50,9）（33,65）（79,75）

1.5 3 1 1.5 2.5 2 4 2

[ET

,LT

] [4,6] [4,7] [2,5] [1.5,4.5] [5,8] [1,4] [3,6] [5,7.5]

a 1 1 1 1 1 1 1 1

b 1 1 1 1 1 1 1 1

Customer 9 10 11 12 13 14 15 16

Coordination (55,35) (78,30) (11,20) (35,93) (73,85) (62,53) (33,13) (9,12)

5 4 1.5 2 4 2.5 45 3

[ET

] [2,4] [2,5] [3,5] [2,4] [3,7] [3,6] [1,2] [0.5,4]

a 1 1 1 1 1 1 1 1

b 1 1 1 1 1 1 1 1

Table 2: Depot and distribution center data.

Depot 18 19 20 17

Coordination （20,20）（75,45）（50,8）（40,40）

Number of model No.1 3 3 3

Number of model No.2 3 3 3

Table 3: Vehicle data.

Vehicle model No 1 2

10 8

0.8 1

0.4 0.6

40 40

VEHICLE ROUTING PROBLEM WITH MULTI-DEPOT AND MULTI-TASK

653

Table 4: Vehicle scheduling situation after optimization.

Starting depot（S） Vehicle model No（K）

Number of Vehicles Driving route

1 1 1 1→4→19→10→6→1

1 2 1 1→4→20→15→1

2 2 1 2→4→18→13→2

2 2 1 2→4→14→9→5→2

3 2 1 3→4→8→17→12→3

3 2 1 3→4→11→7→16→3

Table 5: Vehicle scheduling situation in in stochastic context.

Starting depot（S） Vehicle model No（K）

Number of Vehicles Driving route

1 1 1 1→4→19→10→1

1 2 1 1→4→15→20→6→1

2 1 1 2→4→5→9→14→2

2 2 1 2→4→13→18→2

3 1 1 3→4→8→17→12→3

3 2 1 3→4→16→7→11→3

Experimental parameters used in simulation

example are as follows: α=1, β=2，ρ（t

）=1，

n=100,Q=100,C=3,Max(P

)=10, iteration number is

equal to 50. Finally, we get the total cost that is

425.6. Vehicle scheduling situation can be seen in

Table 4.We also get a stochastic solution in

stochastic selection context, and assume that

stochastic vehicle scheduling situation can be seen in

Table 5. The total cost is 440.92.Simulation results

show that the total cost optimized by the self-

adaptive and polymorphic ant colony algorithm

(APACA) is 425.6, which is less than the total cost

in stochastic selection context that is 440.92. The

results also demonstrate that it is necessary to

optimize the multi-depot, multi-model vehicles and

multi-task vehicle routing problem and that APACA

is an effective and desirable algorithm for solving

the mathematical model.

4 CONCLUSIONS

In the process of city distribution, the optimal

selection of the vehicle route is a key issue to

improve the service quality, reduce the operation

cost and increase the profits. In this paper we present

a new mathematical model of the vehicle routing

problem in the context of city distribution, which

considers multi-depot, multi-model vehicles and

multi-task. The objective function includes three

parts: transport cost, deadheading cost and time cost.

A self-adaptive and polymorphic ant colony

algorithm (APACA) is introduced to solve this

mathematical model. Finally, the effectiveness of the

algorithm is demonstrated by the simulation results.

However, there are some aspects such as target

system, evaluating indicator of route and the

effectiveness of the algorithm that can be improved.

In future studies, more factors such as customer

priority and road condition should be considered

when we establish mathematical models. These will

make the solution more practical and perfect.

ACKNOWLEDGEMENTS

This work is supported by “Dynamic Allocation of

City Logistics Resource Based on the City

Sustainable Development Perspective”, a research

project of the humanities and social sciences of the

Ministry of Education of the People’s Republic of

China (No. 10YJC630324), and supported by

“Allocation of City Logistics Resource”, a project of

the Beijing Municipal Commission of Education

(No. PHR20110877).

REFERENCES

Koehler., 1999. City Logistics in Kassel. City Logistics J:

Letters, 1, 261-271.

Yamada, T., Taniguchi, E., Itoh, Y., 2001. Co-operative

Vehicle Routing Model with Optimal Location of

Logistics Terminals. City Logistics J: Letters. 2, 139-

153.

Renaud, J., Laporte, G., Boctor, F., 1996. A Tabu Search

Heuristic for the Multi-depot Vehicle Routing

Problem, Computers & Operations Research. 23:229–

235.

Yaohuang Guo, Jun li, 1995. A Survey of Logistics

Delivery Vehicle Scheduling. Journal of Xi’an Jiao-

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

654

tong University J: Letters. 30(4), 376-382.

Shengce Hang, Huaizu Li, 1997. The Generalized

Assignment Model and Its Decomposition Algorithm of

Multiple Depot Vehicle Scheduling Problem (MDVSP).

Journal of Xi’an Jiaotong University J: Letters. 31(12),

111-116.

Mingshan Zhang, Xiaowo Tang, 2002. Full Load Vehicle

Routing with Multiple Depots: New Network Flow

Based Algorithm. Joural of Systems Engineering J:

Letters. 17(3), 216-220.

Meijun Chen, Zhisheng,Zhang, Jinfei Shi, 2008. Vehicle

Routing Problem with Multiple Constraints Using

Adaptive and Polymorphic Ant Colony Algorithm.

Journal of Southeast University (Natural Science

Edition). 38(1), 37-42.

Yuan Ding, Yinzhen Li，2004. Greedy Sweep Algorithm

of Conveyance Route Optimization in Logistical

Delivery Management Systems. Journal of Lanzhou

Jiao Tong University J: Letters. 23(6), 140-142.

Nan Jia, Yongbo Lv, 2007. Mathematical Model and

Arithmetic of VRP in Physical Distribution Routing.

Logistics Techology J: Letters.26(4), 54-56.

Shiquan Zhong, Guoguang He, 2005. Study on Multi-

depot Vehicle Scheduling Problem with Time

Windows and Multi-type Vehicle Limits and Its Tabu

Search Algorithm. OR TRANSACTIONS J: Letters.

9(4), 67-70.

Meijun Chen, Zhisheng Zhang, Jinfei Shi, 2007. Study on

Intelligent and Polymorphic Ant Colony Algorithm

Based on Multi-depot Vehicle Routing Problem.

Proceedings of the 7th China ITS Annual Meeting, C:

Letters.

Lei Wen, FanHua Meng, 2008. An Improved PSO for the

Multi-depot Vehicle Routing Problem with Time

Windows. IEEE Pacific-Asia Workshop on

Computational Intelligence and Industrial Application .

852-856.

Kallehauge, Brian, 2008. Formulations and Exact

Algorithms for the Vehicle Routing Problem with

Time Windows. Computers and Operations Research

M: Letters. 2307-2330.

Nabila Azi, Michel Gendreau, 2007. An Exact Algorithm

for a Vehicle Routing Problem with Time Windows

and Multiple Use of Vehicles. Computers and

Operations Research M: Letters. 223-237.

VEHICLE ROUTING PROBLEM WITH MULTI-DEPOT AND MULTI-TASK

655