
PARAMETER ESTIMATION OF AN INDUSTRIAL EVAPORATOR
WITH HYBRID DYNAMICS BY A SMOOTHING APPROACH
Ines Mynttinen
1
, Erich Runge
2
and Pu Li
3
1
Institute of Automation and System Engineering, Technische Universit¨at Ilmenau
Gustav-Kirchhoff-Strasse 1, Ilmenau, Germany
2
Institute of Physics, Technische Universit¨at Ilmenau, Weimarer Strasse 32, Ilmenau, Germany
3
Department of Computer Science and Automation, Technische Universit¨at Ilmenau, Ilmenau, Germany
Keywords:
Parameter estimation, Dynamic optimization, Hybrid systems, Smoothing method.
Abstract:
Evaporation systems are essential in process industries. Due to phase transitions and changes of operating
modes these systems has to be classified as hybrid systems and the simulation and optimization based on
detailed models is often a challenging if not an intractable task. In this study we apply a smoothing approach
in order to modify the hybrid model such that the discrete transitions are integrated into a system of differential
algebraic equations leading to exclusively smooth trajectories. The simulation results of the smooth model are
compared to those of the original hybrid model. With a view to parameter estimation the sensitivity with
respect to the smoothing parameter as well as the parameters to be estimated are calculated. The parameter
estimation is carried out for the smooth model and the dependence of the optimization results on the smoothing
parameter is investigated.
1 INTRODUCTION
Nowadays, simulation and optimization based on
physical models are indispensable tools to improve
design and operation of complex industrial systems.
Optimization problems occur for many tasks such as
parameter estimation, data validation, safety verifica-
tion and model predictive control. The objective of
the respective optimization is subject to the dynamic
model equations of the process under consideration
and possibly to additional equality and inequality con-
straints resulting, e.g., from safety demands. State-
of-the-art methods allow for successfully solving op-
timization problems which include only continuous
system models expressed as a set of differential al-
gebraic equations (DAE). However, in many fields,
e. g., chemical processes, power plants, oil refineries,
continuous and discrete state dynamics are coupled
strongly. Such systems with mixed continuous and
discrete dynamics are called hybrid systems. The dis-
crete dynamics result from instantaneous autonomous
or controlled (externally triggered) transitions from
one operating regime to another. Between these tran-
sition points, the state variables of the system evolve
continuously according to the DAE of the respective
operation mode. Due to the mixed discrete-continuo-
us dynamics, the trajectories of the state variables are
in general non-smooth or even discontinuous, which
may impede the optimization of such systems. Sev-
eral approaches, e.g., mixed-integer programming,
heuristic methods, relaxation and penalization strate-
gies have been proposed to tackle this problem. Since
relaxation strategies are most promising with regard
to the computation time, they will be studied in this
paper. Up to now mostly relatively small systems
have been studied using relaxation methods. In this
study, a large-scale industrial evaporator with switch-
ing behavior is formulated as a hybrid model and as a
relaxed continuous model, respectively. Both models
are simulated and the parameter sensitivities are cal-
culated over the whole time horizon. For the smooth
model, results of the parameter estimation and the de-
pendence of the solution on the reformulation param-
eter are shown.
The paper is organized as follows. The challenges
and solution approaches for simulation and optimiza-
tion of hybrid dynamic systems are discussed in Sec-
tion 2. Section 3 presents the evaporator model in its
hybrid and relaxed form. In Section 4, the simulation
results of the relaxed (and consequently smooth con-
tinuous) model are compared with those of the orig-
inal hybrid model. Section 5 applies our smoothing
31
Mynttinen I., Runge E. and Li P..
PARAMETER ESTIMATION OF AN INDUSTRIAL EVAPORATOR WITH HYBRID DYNAMICS BY A SMOOTHING APPROACH.
DOI: 10.5220/0003575500310036
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
31-36
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

method to two fundamental tasks of process engineer-
ing, namely parameter estimation and the calculation
of sensitivities. Section 6 summarizes the results and
concludes the paper.
2 OPTIMIZATION OF HYBRID
SYSTEMS
Mathematically, discrete transitions in hybrid sys-
tems are often formulated in terms of complementar-
ity conditions. In actual numerical simulation, dis-
crete transitions are almost always handled through
embedded logical statements. At the zero-crossing
points of some switching function, the initial condi-
tions are updated and the appropriate set of equations
is solved restarting at this point in time (Barton and
Lee, 2002). Systems with so-called Filippov solu-
tions that remain for a while at the zero-crossing re-
quire additional analysis. Since they do not pose a
particular problem for our approach, we will not dis-
cuss them further here. A profound analysis and nu-
merical simulation results of hybrid systems can be
found in (Mehrmann and Wunderlich, 2009; Goebel
et al., 2009). For optimization tasks, the hybrid sim-
ulation can be embedded into a heuristic search al-
gorithm. For instance, particle swarm optimization
has been applied by (Pappala and Erlich, 2008) to
the unit commitment problem. These methods suf-
fer from high computational cost when many func-
tion evaluations are needed (i.e. in a high dimen-
sional search space). Alternatively one can consider
the problem as a constrained optimization problem
subject to the dynamic model equations. This leads
to a dynamic nonlinear program (NLP). In the so-
called direct method, the DAE system is discretized
resulting in a large-scale NLP with equality (and pos-
sibly inequality) constraints, which can be solved by
means of a NLP solver with a gradient-based search.
However this NLP-based optimization of hybrid sys-
tems is an extremely challenging task due to the non-
smoothness of the objective function or constraints
which result from instantaneous mode transitions. As
a consequence, NLP regularity cannot be presumed
and NLP solvers may fail. Essentially three different
approaches can be used to overcome this difficulty.
Mixed-integer methods have been applied success-
fully to optimal control problems by (Sonntag et al.,
2006) and (Barton et al., 2006), where a graph search
algorithm explores the state space of the discrete vari-
ables. An embedded NLP is used to find the local
optima in the continuous state space. The complex-
ity study in (Till et al., 2004) indicates that for sys-
tems with many decision variables solving the prob-
lem becomes computationally expensive. The sec-
ond approach applied, e.g., by (Prada et al., 2007)
and (Voelker et al., 2007) comprises sequential op-
timization methods. Here, the optimization layer ex-
clusively contains continuous variables. The hybrid
system is put into the simulation layer and solved
by any simulator which is capable to treat discon-
tinuities. Again, the necessity of many simulation
runs increases the computational cost. Reformulation
strategies, which represent the third class of methods,
introduce additional variables and parameters to re-
move the non-smoothness related to the complemen-
tarity conditions from the problem while retaining the
desired features. Reformulation strategies have been
studied by (Baumrucker et al., 2008; Sager, 2009;
Ralph and Wright, 2004). Most reformulation strate-
gies fall into one of the following two classes: (i)
Relaxation methods transform the complementarities
into a set of relaxed equality or inequality constraints,
e.g., by the smoothing discussed in this contribution.
A sequence of relaxed problems is solved in order to
approach the solution of the original problem. (ii) Pe-
nalization methods introduce a penalization term into
the objective function which measures the violation
of the complementarity condition.
3 MODEL OF THE EVAPORATOR
The evaporation of volatile components to concen-
trate non-volatile components within a mixture is a
common technology in process engineering. Usually
multi-stage systems built up from several identical
single evaporators are used. Such a single evaporator
model is considered in this paper following (Sonntag
et al., 2006). The system consists of an evaporation
Figure 1: Evaporator model (Sonntag et al., 2006).
tank and a heat exchanger (see Figure 1). The tank is
fed through the valveV
1
with a mixture of three liquid
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
32

components A, B, C with mass fractions w
A
, w
B
, w
C
,
where A is a hydrocarbonof high molar mass and thus
has a very low vapor pressure (implemented as P
0
A
= 0
in the model) compared to water (B) and ethanol (C).
Inside the tank, the volatile components are evapo-
rated. Hence the mass fraction of the non-volatile
component A in the liquid is increased. This prod-
uct will be drained from the tank through the valve
V
2
when the desired concentration of A is reached.
The vapor which consists of B and C with the mass
fractions ξ
B
, ξ
C
determined by the phase equilibrium
escapes from the tank through the valve V
v1
. In order
to heat the tank, hot vapor is supplied to the heat ex-
changer, where the vapor condensates and leaves the
heat exchanger as a liquid.
Depending on the pressure inside the evaporator
and the temperature difference between the heat ex-
changer and the tank, M = 4 operating modes can
be distinguished: If the temperature of the heat ex-
changer is higher than that of the tank, the heat ex-
changer operates in the mode ’heating’ (H), other-
wise ’non-heating’ (NH). Inside the tank, the tran-
sition from the mode ’non-evaporating’ (NE) to the
mode ’evaporating’ (E) occurs as soon as the pres-
sure reaches a certain threshold. Hence, during oper-
ation the system may visit the four operating modes:
NE/NH (m = 1), NE/H (m = 2), E/H (m = 3) and
E/NH (m = 4). Thus, the evaporator model pos-
sesses the typical features of a hybrid system with au-
tonomous mode transitions.
3.1 The Hybrid Evaporator Model
The hybrid model of the evaporator consists of four
sets of DAE f
(m)
( ˙x,x, p) = 0, m = 1,...,M which can
be found in (Sonntag and Stursberg, 2005). The
tank and the heat exchanger change their operation
mode when the respective state-dependent switching
function ψ
(1)
(p) = p− p
c
, p
c
= 0.4bar or ψ
(2)
(T) =
T − T
heatex
crosses 0. T and p denote the tempera-
ture and the pressure in the tank. As a consequence of
this zero-crossing, the dynamics change and the state
variables immediately before the switch x
−
have to
be mapped onto the state variables immediately after
the switch x
+
using the so-called transition functions
x
+
= T (x
−
). For instance, for the vapor mass fraction
ξ
B
the transition function from the non-evaporating
modes (m = 1,2) to the evaporating modes (m = 3, 4)
reads
ξ
+
B
= ξ
−
B
+
w
B
P
0
B
(T)
w
A
P
0
A
(T) + w
B
P
0
B
(T) + w
C
P
0
C
(T)
(1)
with the temperature T
+
= T
−
= T and the liquid
mass fractions w
+
= w
−
= w.
3.2 A Smooth Evaporator Model
State trajectories are in general non-smooth or even
discontinuous at the transition points. If such a model
is included into an optimization problem, these points
are severe obstacles for gradient-based optimization
algorithms. In order to make the optimization of hy-
brid systems accessible to NLP solvers, the comple-
mentarity condition of the original problem is relaxed,
i.e., the strict complementarity conditions are fulfilled
only approximately. In our smoothing approach, we
replace the if-else-statement by the smoothing func-
tion
ϕ(x) =
1+ exp
−
ψ(x)
τ
−1
(2)
with the small smoothing parameter τ. The model
equations are combined in one single set of equations
according to
f( ˙x,x, p) = ϕ(x) f
(1)
( ˙x,x, p)
+ (1 − ϕ(x)) f
(2)
( ˙x,x, p). (3)
This reproduces the switching behavior of the hybrid
model in the limit τ → 0.
4 SIMULATION RESULTS
Figure 2 shows that the trajectories of the smooth
model with smoothing parameter τ = 0.002bar and
of the original hybrid model deviate only marginally
from each other. When the pressure meets the tran-
sition condition p = p
c
(see inset of Figure 2(a)) the
evaporator switches from the non-evaporating mode
to the evaporating mode. As a consequence, the mass
fractions of the volatile components B and C jump ac-
cording to Eq. 1 from 0 in the non-evaporating mode
(no vapor is present) to the finite values given by the
phase equilibrium (see Figure 2(b)) and vaporstarts to
escape from the tank (Figure 2(c)). The evaporation
of the volatile components B and C leads to a decrease
of their mass fractions w
B
, w
C
in the liquid. The de-
crease of w
C
(ethanol) is more pronounced due to
the higher vapor pressure and thus the higher outflow
of C. Consequently, the vapor mass fractions cross
each other near t = 1150s (Figure 2(b)). Since the
pressure in the evaporator and also the vapor outflow
(Figure 2(a) and 2(c)) depend on the (temperature-
dependent) vapor pressure and the mass fractions of
all liquid components, both first increase due to the
increasing temperature and later decrease due to the
reduced mass fractions w
B
, w
C
in the liquid.
Figure 3 demonstrates that the smooth model ap-
proximates the hybrid model the better the smaller
PARAMETER ESTIMATION OF AN INDUSTRIAL EVAPORATOR WITH HYBRID DYNAMICS BY A
SMOOTHING APPROACH
33
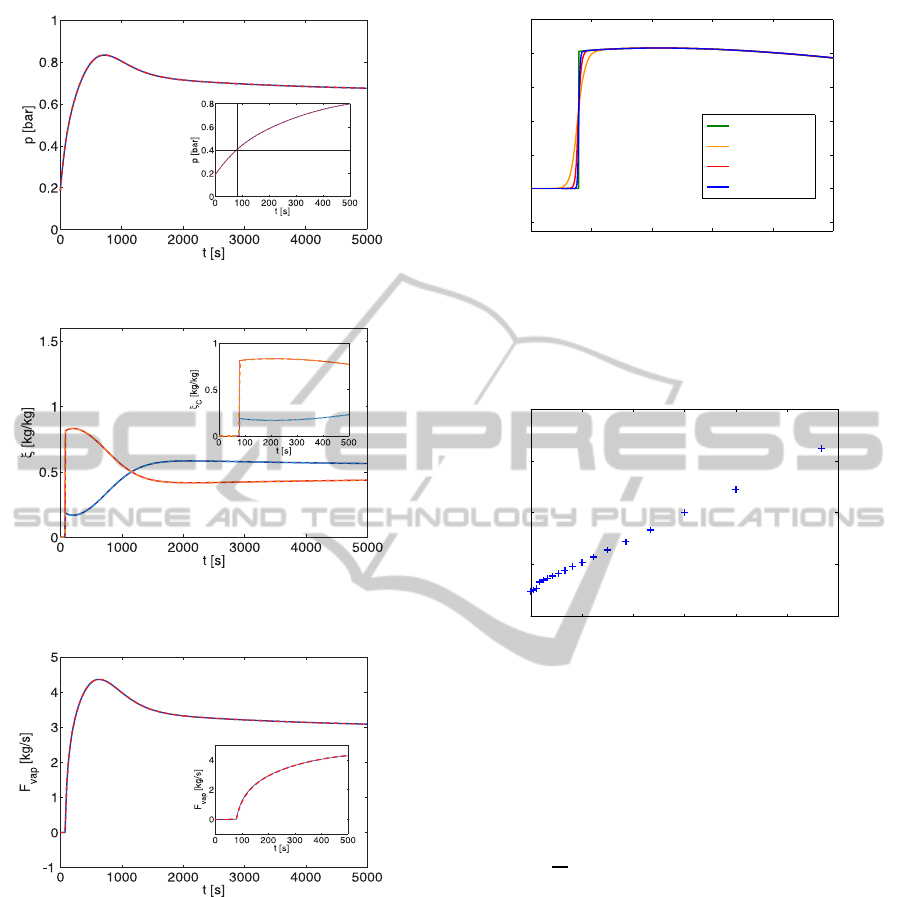
(a) Pressure inside the evaporator for the hybrid model (blue) and the
smooth model (red).
(b) Mass fractions of the volatile components B (hybrid model: dark blue,
smooth model: light blue) and C (hybrid model: red, smooth model: orange)
in the vapor.
(c) Vapor flow from the evaporator for the hybrid model (blue) and the
smooth model (red).
Figure 2: Simulation results of the hybrid and the smooth
model.
the smoothing parameter τ is chosen: The slope of
the state trajectory ξ
C
increases and the transition re-
gion narrows. In the transition region, the dynamics is
given by the linear combination (Eq. 3) of both oper-
ation modes involved. It is important to note that the
trajectories of the hybrid model and the smooth ap-
proximation are nearly identical outside the transition
region. Obviously, the smoothing only extends the
transition time but does not drive the system to a dif-
ferent region of the state space. From this result we
conclude that the smoothing approach is well suited
0 100 200 300 400 500
−0.2
0
0.2
0.4
0.6
0.8
t [s]
ξ
C
[kg/kg]
hybrid
τ=0.01 bar
τ=0.004 bar
τ=0.002 bar
Figure 3: Mass fraction ξ
C
from simulations with several
values of the smoothing parameter.
for the evaporator model.
2 4 6 8 10 12 14
x 10
−3
0
1
2
3
4
x 10
−3
τ [bar]
s [kg
2
/kg
2
]
Figure 4: Deviation of the smooth model from the hybrid
model as a function of the smoothing parameter.
For a more quantitative analysis of the convergence
of the solutions of the relaxed model to that of the
original model, we consider in Figure 4 the average
squared deviation
s =
1
N
N
∑
i=1
ξ
(hybrid)
C
(t
i
) − ξ
(smooth)
C
(t
i
)
2
(4)
between the vapor mass fractions ξ
C
calculated with
the hybrid and the smooth model. The average
squared deviation is found to follow approximately
s ∝ τ and is dominated by the finite width of the tran-
sition region.
5 PARAMETER ESTIMATION
AND SENSITIVITY ANALYSIS
A fundamental task frequently occurring in process
engineering is parameter estimation. Parameter esti-
mation in general aims at extracting the best guesses
of the parameters determining the dynamics of the
system under consideration based on a series of
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
34
measurements x
(m)
ij
of several state variables x
i
, i =
1,...,M at different points in time t
j
, j = 1,...,N. It
is useful to combine the parameter estimation of a hy-
brid system with the sensitivity analysis for at least
two reasons: First, the sensitivities of the measured
state variables with respect to the parameters to be
estimated allow to evaluate the applicability of cer-
tain data in a parameter estimation problem. Second,
the sensitivity with respect to the smoothing param-
eter is needed to predict the suitability of the smooth
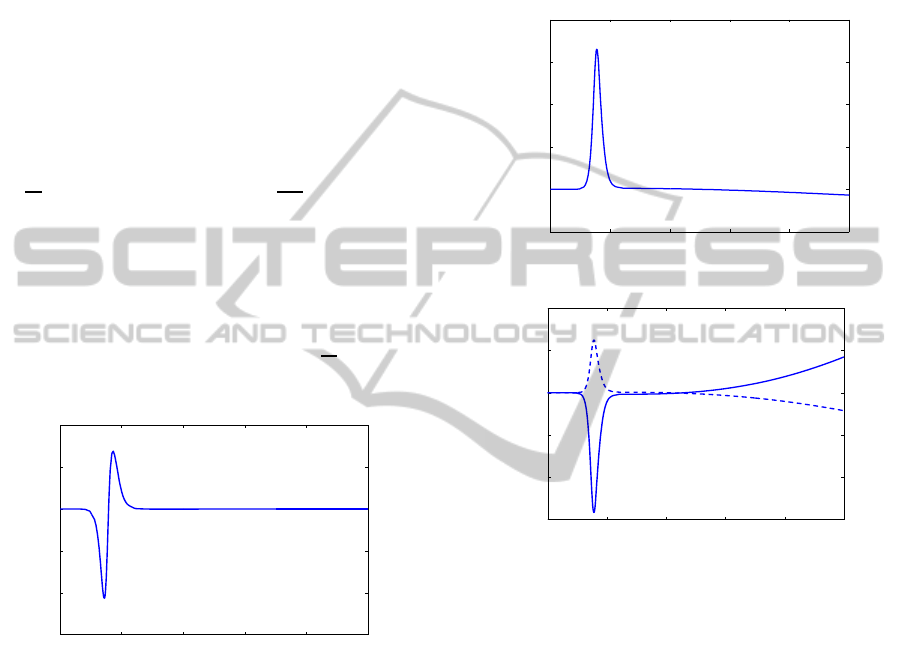
model for parameter estimation. The sensitivity of the
state variable ξ
C
with respect to the smoothing pa-
rameter (Figure 5) quantifies the observation already
stated qualitatively in Section 4 that the influence of
the smoothing is restricted to the transition region,
i.e.,
dξ
dτ
≈ 0 outside. The shape of
dξ
C
dτ
is easily un-
derstood in view of the trajectory shown in Figure 3.
As τ increases, i.e., ∆τ = τ
2
−τ
1
> 0, the curve ξ
C
(τ
2
)
lies above that of ξ
C
(τ
1
) as long as p < p
c
and thus
∆ξ
C
= ξ
C
(τ
2
) − ξ
C
(τ
1
) is negative, whereas it is posi-
tive when p > p
c
. In Figure 5, the sensitivity is calcu-
lated at the rather large parameter value τ = 0.01bar.
A smaller τ yields narrower regions with
dξ
dτ
6= 0 (not
shown).
0 100 200 300 400 500
−3
−2
−1
0
1
2
x 10
−3
t [s]
dξ
C
/dτ |
τ=0.01 bar
Figure 5: Sensitivity with respect to the smoothing parame-
ter.
Below, we will estimate the coefficient k of the
heat transfer from the heat exchanger to the tank,
the valve throughputs of the liquid inflow (V
1
) and
the liquid outflow (V
2
) based on measurements of the
ethanol vapor mass fraction ξ
C
. This choice of the
measured variable is due to the fact that ξ
C
is one of
the quantities with the most significant hybrid behav-
ior, which shows up as a jump at the mode transition
(Figure 2(b)). As can be seen in Figure 6, the corre-
sponding sensitivities are relatively large around the
mode transition. The most dominant influence of the
heat transfer and the liquid in- and outflow, i.e., the
mass of liquid to be heated is indirect via the tran-
sition time NE → E. An increase of the heat trans-
fer coefficient or a decrease of the liquid inflow shifts
the curve ξ
C
(t) to the left, i.e., accelerates the pro-
cess. Hence the respective sensitivities are positive
and negative in the first time period and change sign
when ξ
C
(t) exceeds its maximum. Based on Figure 6,
one can expect to find the correct parameter values by
means of parameter estimation, if ξ
C
data are avail-
able around the transitions or in the late time period.
0 100 200 300 400 500
−0.01
0
0.01
0.02
0.03
0.04
t [s]
dξ
C
/dk |
k=4 kW/m
2
K
(a) Sensitivity with respect to the heat transfer coefficient.
0 100 200 300 400 500
−0.3
−0.2
−0.1
0
0.1
0.2
t [s]
dξ
C
/dV|
V
1
=7.0 kg/s,V
2
=2.0kg/s
* 10
(b) Sensitivity with respect to the valve throughputs (liquid inlet: solid, liq-
uid outlet: dashed).
Figure 6: Sensitivities of the mass fraction of component C.
The ’measurement data’ for our parameter esti-
mation have been generated by simulation of the hy-
brid system with added Gaussian distributed mea-
surement error (σ = 0.04kg/kg). We use a series
of 51 equidistant data points within the time hori-
zon t ∈ [0,500] s. As usual, the parameter esti-
mation problem is formulated as least-square opti-
mization. Figure 7 shows the simulation results of
the hybrid model and the optimization result for a
particular realization of ’measurement data’. The
corresponding optimal parameter values (k
(opt)
=
4.070kW/m
2
K, V
(opt)
1
= 6.968kg/s and V
(opt)
2
=
1.950kg/s) agree very well with the values used for
the data generation (k
(opt)
= 4.0kW/m
2
K, V
(opt)
1
=
7.0kg/s and V
(opt)
2
= 2.0kg/s). The optimal param-
eters are quite robust regarding the smoothing pa-
rameter (not shown). However, the optimal objec-
tive function values are considerably influenced by
PARAMETER ESTIMATION OF AN INDUSTRIAL EVAPORATOR WITH HYBRID DYNAMICS BY A
SMOOTHING APPROACH
35
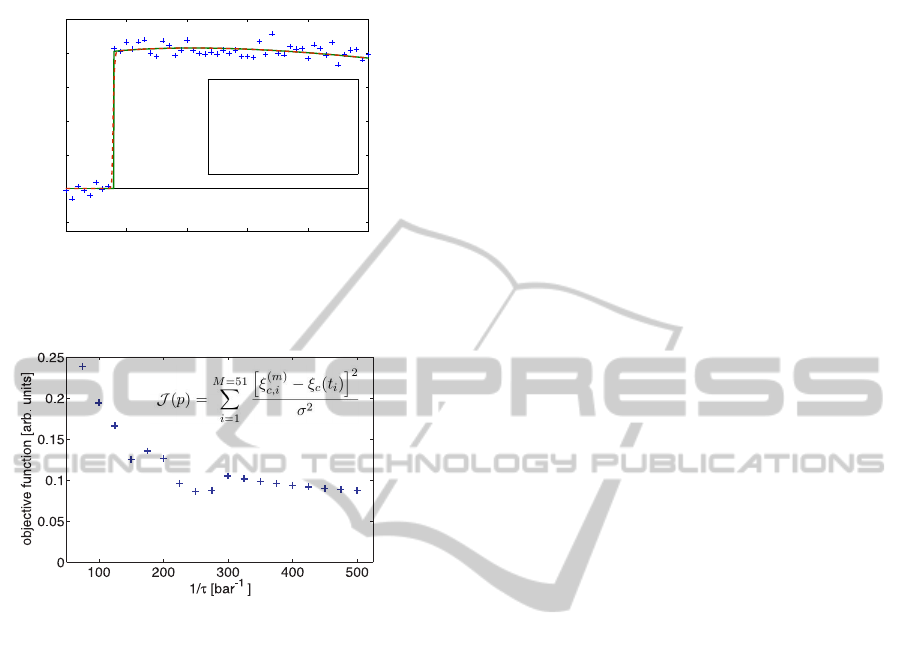
the smoothing parameter (see Figure 8).
0 100 200 300 400 500
−0.2
0
0.2
0.4
0.6
0.8
t [s]
ξ
C
[kg/kg]
k
(opt)
= 4.070 kW/m
2
K
V
1
(opt)
= 6.968 kg/s
V
2
(opt)
= 1.950 kg/s
Figure 7: Parameter estimation result (dashed), measure-
ment (cross) and simulation of the hybrid model (solid).
Figure 8: Optimal objective function values as a function of
the smoothing parameter.
6 CONCLUSIONS
In this study, we carried out the parameter estimation
accompaniedby sensitivity analysis for a hybrid evap-
orating system using a smoothing approach. We first
investigated a smooth approximated model by means
of simulation of the evaporator dynamics for differ-
ent values of the smoothing parameter. Performing
the sensitivity analysis with respect to the parame-
ters to be estimated we could evaluate the usability
of the measurement of a certain variable for the pa-
rameter estimation. The sensitivity with respect to the
smoothing parameter is studied to evaluate the suit-
ability of the smooth model for the purpose of param-
eter estimation. It is shown the proposed method can
successfully determine the correct parameter values.
The results turned out to be quite robust against the
variation of the smoothing parameter. Future work
will extend the model for control tasks and finally op-
timize the plant operations.
REFERENCES
Barton, P. I. and Lee, C. K. (2002). Modeling, simulation,
sensitivity analysis, and optimization of hybrid sys-
tems. ACMT. Model. Comp. S., 12(4):256–289.
Barton, P. I., Lee, C. K., and Yunt, M. (2006). Optimiza-
tion of hybrid systems. Comp. Chem. Eng., 30(10-
12):1576–1589.
Baumrucker, B. T., Renfro, J. G., and Biegler, L. T. (2008).
MPEC problem formulations and solution strategies
with chemical engineering applications. Comp. Chem.
Eng., 32(12):2903–2913.
Goebel, R., Sanfelice, R. G., and Teel, A. R. (2009). Hybrid
dynamical systems. IEEE Control Syst. Mag., pages
28–93.
Mehrmann, V. and Wunderlich, L. (2009). Hybrid systems
of differential-algebraic equations - analysis and nu-
merical solution. J. Process Contr., 19(8):1218–1228.
Pappala, V. S. and Erlich, I. (2008). A new approach for
solving the unit commitment problem by adaptive par-
ticle swarm optimization. In Power and Energy Soci-
ety General Meeting, 2008 IEEE, pages 1–6.
Prada, C. D., Cristea, S., and Rosano, J. J. (2007). Optimal
start-up of an evaporation station. In 8th International
IFAC Symposium on Dynamics and Control of Process
Systems, volume 3, pages 115–120.
Ralph, D. and Wright, S. J. (2004). Some properties of
regularization and penalization schemes for MPECs.
Optim. Method. Softw., 19(5):527–556.
Sager, S. (2009). Reformulations and algorithms for the op-
timization of switching decisions in nonlinear optimal
control. J. Process Contr., 19(8):1238–1247.
Sonntag, C., Stursberg, O., and Engell, S. (2006). Dynamic
optimization of an industrial evaporator using graph
search with embedded nonlinear programming. In 2nd
IFAC Conference on Analysis and Design of Hybrid
Systems, pages 211–216.
Sonntag, C. and Stursberg, O. (2005). Safety verification of
a discretely controlled evaporation system. In Techni-
cal Report, HYCON, pages 1–20.
Till, J., Engell, S., Panek, S., and Stursberg, O. (2004). Ap-
plied hybrid system optimization: An empirical inves-
tigation of complexity. Control Eng. Pract., 12:1291–
1303.
Voelker, A., Sonntag, C., Lohmann, S., and Engell, S.
(2007). Optimization-based safety analysis of an
industrial-scale evaporation system with hybrid dy-
namics. In 8th International IFAC Symposium on Dy-
namics and Control of Process Systems, volume 1,
pages 117–122.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
36
