STUDY OF WIND FARM BEHAVIOUR DURING POWER

SYSTEM NETWORK DISTURBANCE

T. R. Ayodele, A. A. Jimoh, J. L. Munda and J. T. Agee

Department of Electrical Engineering, Tshwane University of Technology, Pretoria, South Africa

Keywords: Wind farm, Doubly fed induction generator, Power system, Disturbance.

Abstract: This paper studies the impact of disturbances emanating from the power system network on the behaviour

of a wind farm (WF) consisting of doubly fed induction generator (DFIG). Response of the WF to

disturbances like fault occurence, sudden change in load, sudden loss of transmission line and loss of

generation are considered in the study. The models of various systems making up the wind conversion

system are presented. Pitch control system is used for the stabilization of the wind turbine against the

disturbances. Parts of the key results show that the generator inertia, converter controller and types of

disturbance have significant effect on the response of a WF.

1 INTRODUCTION

A lot of efforts are geared towards grid integration

of renewable energies as a result of environmental

concern and energy security. Among these

renewable energies, wind energy stands out as it has

the ability to produce electricity in the MW range.

At present, the wind power growth rate stands at

20% annually and it is predicted that 12% of the

world electricity may come from wind power by the

year 2020 (El-Sayed, 2010). There is tendency to

surpass this rate with the present advancement in the

offshore wind farm techologies.

There are various types of wind turbines in use

around the world each having its own advantages

and disadvantages (Slootweg et al., 2001). The most

used one is the variable speed wind turbine with

doubly fed induction generator (DFIG) due to the

numerous advantages it offers over others et al.,

2005).

The behaviour and the characteristic of the

conventional generators for electricity generation are

well known by the utility operators. With the advent

of wind power, different types of generator

technologies are introduced to the power system.

This poses a lot of concern to most utility operators

as the response of these generators to network

disturbance is not well understood.

Most existing literature is focused on the analysis

of the behavior of power system network as a result

of wind farm integration (Eping et al., 2005; Xing et

al., 2005; Naimi and Bouktir 2008; Folly and

Sheetekela, 2009). This paper looks at it from the

other angle by studying the response of the wind

farm to disturbance in the power system network.

The study is limited to Wind farm (WF) consisting

of variable speed DFIG.

The structure of the remaing part of the paper is

as follows, section two presents the model of the

wind conversion system made of variable speed

DFIG. Section three describes the system under

study. Simulation results obtained are discussed in

section 4 while section five presents the conclusion.

2 MODELLING OF DFIG WIND

CONVERSION SYSTEM

Wind conversion system comprises of the

aerodynamic system, the mechanical shaft system,

electrical system of the induction generator, the

pitch control system, the speed control system, the

rotor side converter controller and the grid side

converter controller. All these systems are combined

together to form a unit system of a wind farm.

2.1 Aerodynamic Torque Model

Aerodynamic model involves the extraction of

241

Ayodele T., Jimoh A., Munda J. and Agee J..

STUDY OF WIND FARM BEHAVIOUR DURING POWER SYSTEM NETWORK DISTURBANCE.

DOI: 10.5220/0003576202410248

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages

241-248

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

useful mechanical power from the available wind

power. Available wind power is given by

wind

PRV

ρπ

(1)

where

wind

and

are the available power in

the wind, air density, radius of the turbine blade and

the wind speed that reaches the rotor swept area. The

fraction of wind power that is converted to the

turbine mechanical power

is given by

()

PRCV

ρπ λ β

(2)

where

C gives the fraction of available wind power

that is converted to turbine mechanical power,

and

are the tip speed ratio and the pitch angle

respectively. The

C ,

and

are related by

equation 3 and 4 (El-Sayed and Adel, 2010)

()

134 6

Ccccec

ββλ

⎛⎞

=−− +

⎜⎟

⎝⎠

(3)

1 1 0.035

10.08

λβ

=−

(4)

Given

=0.5176,

=116,

=0.4,

=5,

=21 and

=0.0068 ,the relationship between

C against

at various

is given in figure 1

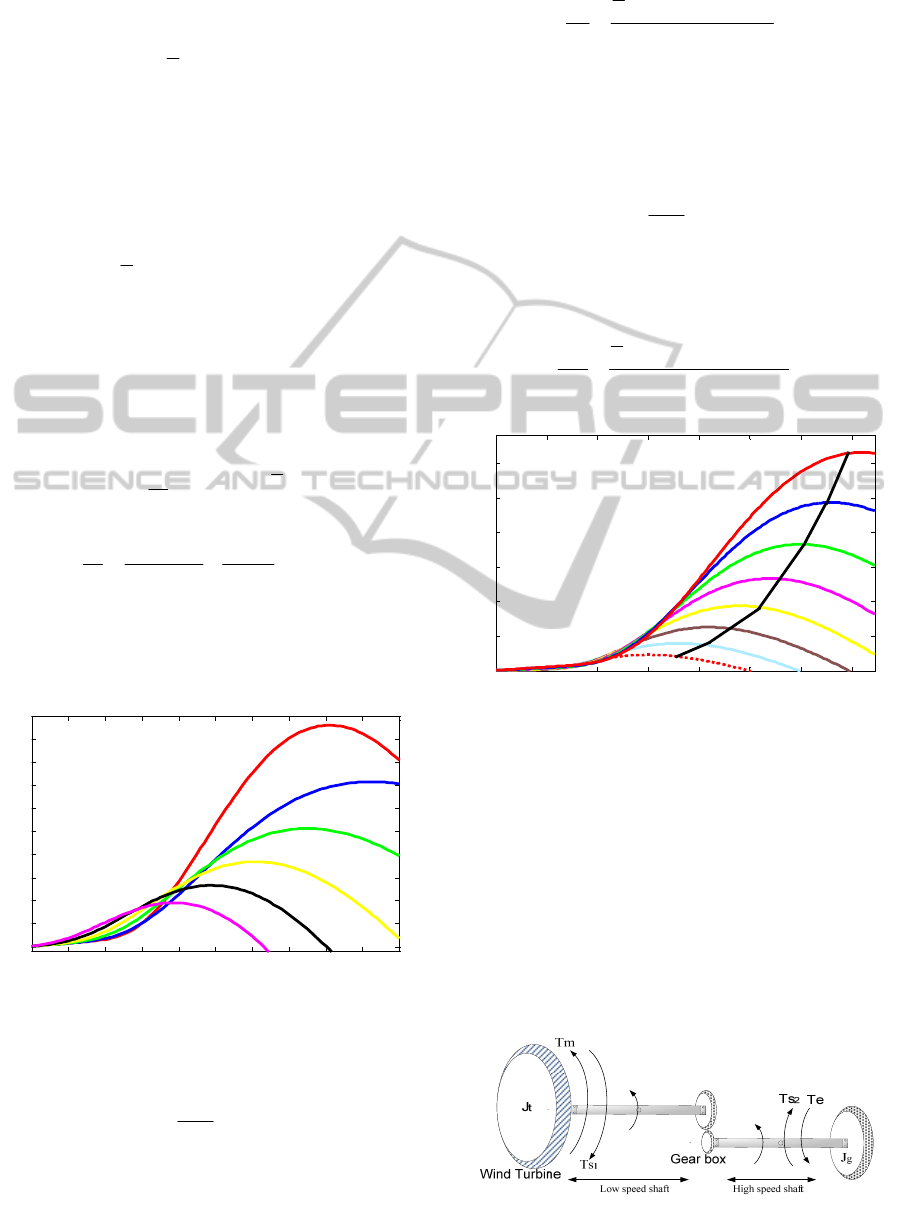
Figure 1: Relationship between Power coeficient and tip

speed ratio at different pitch angle.

The tip speed ratio is given by (5)

(5)

The mechanical torque developed by the wind power

()

RC V

ρπ λ β

ωω

(6)

where

is the turbine speed.

For efficient wind power capture by the variable

wind turbine (Arifujjaman et al., 2009),

opt

therefore (5) can be re-written as

opt

(7)

subtituting (7) in (6), Optimum torque can be

obtained

()

popt

opt

ttopt

RC R

ρπ λ β

ωλ

(8)

Figure 2: Maximum torque tracking of a variable speed

wind turbine.

2.2 The Mechanical Shaft System

Model

Adequate model of the mechanical drive train is

required when the study involves the response of a

system to heavy disturbances. It is better to represent

the shaft by at least two- mass model (Poller, 2009).

Model of the shaft system with two mass models is

presented. The turbine is coupled to the generator

through a gearbox as shown in figure 3

Figure 3: Two mass model of the mechanical shaft system.

0 1 2 3 4 5 6 7 8 9 10

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Tip speed ratio

Power coefficient, Cp

B=20

B=25

B=15

B=10

B=5

B=0

0 0.2 0.4 0.6 0.8 1 1.2 1.4

0.2

0.4

0.6

0.8

1.2

1.2 pu

6 m/s

7.2 m/s

8.4 m/s

9.6 m/s

10.8 m/s

12 m/s

13.2 m/s

14.4 m/s

Turbine speed (pu)

Turbine Torque

Turbine Torque Characteristics at various wind speed (Pitch angle beta = 0 deg)

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

242

From the figure, the following equations can be

derived (9)-(16)

HTTs

=−

(9)

gTsT

=−

(10)

where

and

nP nP

(11)

1111

Ts K F

=−

and

2222

Ts K F

=−

(12)

12eq

θθ

=−

Ts Ts

(13)

eq eq eq eq

TK F

(14)

=−

(15)

ωω

dθ

−=

(16)

where

are the pu turbine and generator

inertia respectively.

and

are the inertia in

kgm

is the electromechanicl torque developed

by the induction generator,

is the pu mechanical

torque applied to the turbine by the wind as given in

(5) .

T are the torques developed by the

shaft at the low speed side, torque developed by the

shaft at the high speed side and the equivalent torque

developed by the shafts respectively.

and

are

the pu turbine and generator rotor speed.

and

are shaft stiffness at low speed side, shaft

stiffness at high speed side and the total shaft

stiffness.

and

are the damping coefficient

of the shaft at the low speed side, high speed side

and the equivalent damping coefficient of the shaft

respectively.

and

θ are the angle of twist of

the shaft at low speed, high speed and the equivalent

angle of twist of the shaft respectively.

n is the

number of pole pair, n is the gear ratio,

P is the

generator active power,

where

is the

frequency.

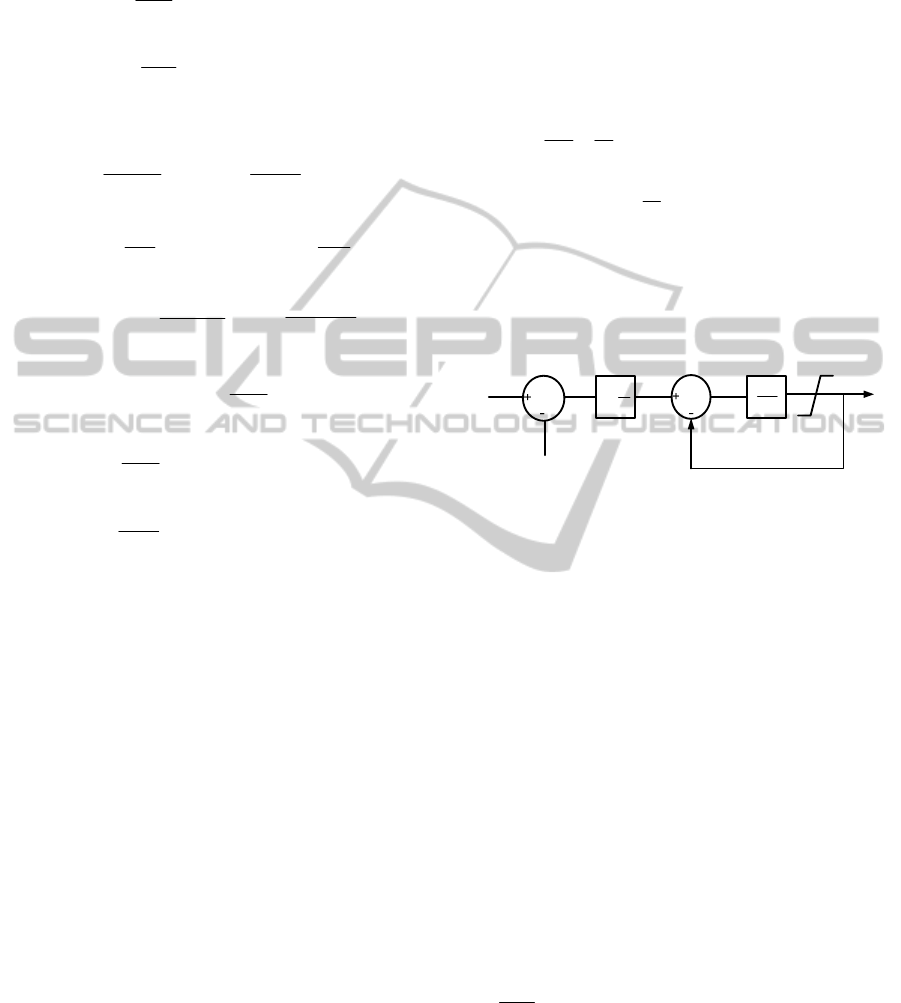
2.3 Pitch Angle Controller Model

Pitch angle controller majorly serves a purpose of

limiting the generated power to the rated power in

the time of high wind speed. It also limits the speed

of the generator during heavy disturbances. The

pitch controller based on PI is given by (17) (El-

Sattar et al., 2008)

()

ref

ref P ref m

kPP

ββ

=−

⎛⎞

=+ −

⎜⎟

⎝⎠

(17)

where

ref

is the reference pitch control,

and

are

the proportional and integral parameter of the PI

controller,

ref

P is the reference turbine power

Figure 4: Pitch angle controller.

2.4 Wind Generator Model

Most wind farms are made of induction generators

because they are cheap and robust. The dq stator and

rotor voltage equations model in generating mode

are as follows (Lipo 2000; Krause et al., 2002). The

equation presented is a fifth order model. Third

order model is obtained by neglecting the transient

term in the stator voltage equation.

qs s qs qs qs

vri p

λλ

−− −

(18)

ds s ds qs ds

vri p

λλ

−+ −

(19)

(

)

qr r qr r qr qr

vri p

ωλ λ

=− − − −

(20)

(

)

dr r dr r qr dr

vri p

ωλ λ

=− + − −

(21)

where

are the stator and rotor speed resistance,

(

)

term.

The stator and rotor flux equations are

qs s qs m qr

Li L i

(22)

ds s ds m dr

Li L i

(23)

Re f

max

mi n

STUDY OF WIND FARM BEHAVIOUR DURING POWER SYSTEM NETWORK DISTURBANCE

243

qr r qr m qs

Li L i

(24)

dr r dr m ds

Li L i

(25)

where

are the stator, rotor and magnetzing

inductance respectively.

, ,

and

are the

stator and rotor d-axis and q-axis.

The electromechanical torque,

developed by

the induction generator in pu can be derived as (26)

given by

()

eqsdrqrds

λλλ

=−

(26)

where

=−

The equation is completed by the mechanical

coupling equation in pu between the turbine and the

generator using two mass model as derived in (9)-

(16)

()

Ts T

dt H

=−

the active and reactive power generated by the

induction generator is given as

()

qs qs ds ds

Pvivi=+

(27)

()

qs ds ds qs

Qvivi=−

(28)

2.5 Grid Connection of DFIG Wind

Farm

DFIG technology makes use of wound rotor. The

stator is directly connected to the grid while the rotor

is coupled to the grid through a Pulse width

modulation (PWM) frequency converter as shown in

figure 4. The converter carries only the rotor slip

power typically in the range of 10-15% of the

generated power (Veganzones et al., 2005).

Figure 5: DFIG with PWM converter control system.

For dynamic study of DFIG, the converter

controller model is important. Stator flux oriented

control is commonly used in the decoupled control

of DFIG.

2.6 DFIG Rotor Side Converter

Controller

The control of the DFIG rotor is done in a

synchronous rotating reference frame i.e

equation (18)-(21). The rotor side converter controls

the stator active and reactive power of the DFIG. By

alligning the dq reference frame in the stator flux

reference frame, then

v =

qs s

vv= ,0

and

ds s

. Subtituting these in (22)-(25), (27), (28)

and re-arranging, we obtain

sqr

=−

(29)

smdr

QvLi

⎛⎞

=−

⎜⎟

⎝⎠

(30)

The rotor voltage equation governing the active

and reactive power control can be obtained by

rearranging equation (18)-(25) and is given by (31)

and (32) (Krause et al., 2002)

()

dr dp dr dr e r r qr

vk ii Li

ωωσ

⎛⎞

=+ −−−

⎜⎟

⎝⎠

(31)

(32)

where,

k ,

are the PI proportional and integral

constant for the d-axis for the control of reactive

power while gain

are the PI constant for

controlling the active power.

and

are the

reference current for the active and reactive power

respectively.

and

are the dq reference voltage

which will be converted to a-b-c frame to generate

command for the rotor end PWM converter. The

block diagram is shown in figure 6a and 6b

2.7 DFIG Grid Side Converter

Controller

The main objective of grid side controller is to

maintain the dc link between the back to back PWM

converters at constant voltage irrespective of the

direction of power flow (Krause et al., 2002). The dq

,ref ref

,dcref ref

()

qr qp qr qr e r r dr S

vk ii Li

ωσ λ

⎛⎞⎛⎞

=+ −+− −

⎜⎟

⎝⎠ ⎝ ⎠

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

244

−

()

ωσ

−

()a

()

er s

ωλ

−

(

)

er r

ωσ

−

()b

Figure 6: Rotor side Controller system.

voltage for the grid side converter is represented by

(33) (Soares et al., 2009)

qq eidq

dd eiqd

vRiL Lv

=+ + +

=+ − +

(33)

Re-arranging 33 with 0

, the governing voltage

equation for the grid side converter can be obtained

()

qp qqeid

dpddeiqd

vk iiL

vk iiLv

⎛⎞

=− + − −

⎜⎟

⎝⎠

⎛⎞

=− + − + +

⎜⎟

⎝⎠

(34)

where

1 p

k ,

are the q axis PI propornal and the

integral constant.

2 p

k ,

are the d axis PI

proportionality and integral constant respectively.

and

are the reference voltage that generates

the command for the grid side PWM converter after

conversion to abc frame.

is derived from the grid

reactive power error while

is derived from the dc

link voltage error as shown in figure 7a and 7b

respectively.

3 SYSTEM UNDER STUDY

The system considered for the study is shown in

figure 8. It consists of 110MW, 50MVAR

synchronous generator (SG) connected to bus 4

through a 20/400kV transformer.

−

()a

Figure 7: Grid side controller system.

DFIG

Turbine

0.69 / 20K

20 / 400

Figure 8: The system under study.

The wind farm (WF) is made up of 40 wind

turbines of 2MW, 0.69kV each modelled as an

aggregate wind turbine. Aggregate model reduces

simulation time required by detailed multi turbine

system (Conroy and Watson 2009). It is assumed

that the wind farms are located far from the point of

common connection (PCC) where the wind

resources are abundantly located as the case for most

real wind farms. The WF is connected to the PCC

through two 20km line (to allow disconnection of a

line) and 69/20KV transformer. The WF is feeding a

60MW, 25MVAR local load connected to bus2

(B2). Another 100MVA, 30MVAR load is

connected to the high voltage bus (B4). The whole

system is connected to a strong grid through a two

400kV, 100km transmission lines.

4 THE SIMULATION RESULT

AND DISCUSSION

Different scenarios were created to get insight into

the response of WF to disturbances from the grid.

First, the response of the wind farm was studied

when there is a step change of 20% in the local load

connected to B2 at 1s. The results with the rotor

controller in place and out of place are depicted in

−

()

STUDY OF WIND FARM BEHAVIOUR DURING POWER SYSTEM NETWORK DISTURBANCE

245

figure 9. From the figure it can be observed that with

the controller in place, the active power (the

negative values indicate a power injected into the

grid) and the electrical torque are immediately

returned to the pre-disturbance level. The step

increase in the local load resulted in a dip in the

terminal voltage and an increase in the speed of the

generator, however, it stabilizes to a new value

almost immedately. This is as a result of change in

the system configuration. With the rotor controller

out, the system is stable but it takes about 3s for the

wind farm to stabilize.

Figure 9: The response of (a) DFIG speed (b) Active

power, (c) Electrical torque (d) Terminal voltage to 20%

step change in local load at 1s.

The response of the wind farm to different fault

type of duration 200ms was investigated. The fault

considered are three phase fault, two phase to

ground fault, phase to phase fault and single phase to

ground fault. The fault was created at 1s at the

middle of 100km, 400kV line. The results are

presented in figure 9. The severity of the impact of

these faults is in the order listed in the legend. This

is evident in the speed, the active power, the

electrical torque and the rotor current in figure 10.

The speed of the generator is limited by the pitch

angle. The first swing of the rotor current reached a

value of 2pu from the prefault value of 0.8pu for a

three phase fault, 1.5pu for two phases to ground

fault, 1.3pu for phase to phase fault and 1pu for

phase to ground fault.

The response of the wind farm to different fault

locations was examined. To get insight into this

scenario, a three phase fault of 200ms duration was

created at different location on the 50km, 20kV line.

The result is shown in figure 11. From the result, the

impact of fault at different location has almost the

same impact on the response of the wind farm.

However, the impact is visibly different at the PCC.

The closer the fault location to the PCC, the more

the dip in voltage and the more the deviation from

the nominal grid frequency.

Figure 10: Response of the wind farm (a) speed (b) Active

power (c) pitch controller (d) Turbine power (e) rotor

current to different types of fault.

Figure 11: Response of (a) DFIG speed (b) DFIG active

power (c) PCC frequency and (d) PCC voltage to 3 phase

fault (200ms duration) at different location on the 20kV

line.

Figure 12 shows the response of the wind

generator with different rotor inertia to a three phase

fault created at the middle of 400kV line. The effect

0 1 2 3 4 5

1.18

1.2

1.22

1.24

(a) Time (s)

DFIG Speed (pu)

0 1 2 3 4 5

-1

-0.9

-0.8

-0.7

-0.6

(b) Time (s)

Active power (pu)

0 1 2 3 4 5

0.7

0.8

0.9

Electrical torque (pu)

0 1 2 3 4 5

0.645

0.65

0.655

0.66

(d) Time (s)

Terminal voltage (kV)

With rotor side controller Without rotor side contoller

0 0.5 1 1.5 2 2.5 3

1.15

1.25

1.35

(a) Time (s)

DFIG Speed (pu)

0 0.5 1 1.5 2 2.5 3

-1

-0.5

0.5

(b) Time (s)

Active Power (pu)

0 0.5 1 1.5 2 2.5 3

-0.5

0.5

(d) Time (s)

Electrical torque (pu)

0 0.5 1 1.5 2 2.5 3

Pitch angle

0 1 2 3

0.5

1.5

(e) Time (s)

Rotor current (pu)

3-phase fault

2 phase to ground fault

Phase to phase fault

Phase to ground fault

Legend

0 1 2 3

1.15

1.2

1.25

1.3

1.35

(a) Time (s)

DFIG Speed (pu)

0 1 2 3

-0.8

-0.6

-0.4

-0.2

(b) Time (s)

Active power (pu)

0 1 2 3

Freq at PCC (Hz)

0 1 2 3

(d) Time (s)

PCC Voltage (kV)

0% 30% 70% 100%

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

246

of inertia can be noticed in the speed of the

generator. The generators with larger inertia are

more stable in case of fault compared to the

generator with smaller inertia. The first swing in

rotor speed for 50kgm

is 1.28pu, 1.26pu for

100kgm

, 1.24pu for 150kgm

and 1.22pu for

200kgm

2 .

No distict difference in the response of the

active power, electrical torque and the terminal

voltage are seen.

Figure 12: Wind farm with DFIG of different inertia.

The effect of a loss of transmission line (TL) and

generation was studied. For the TL, the circuit

breaker at both ends of the lines were opened at 1s

for the 400kV, 100km line and then for 20kV, 50km

line. The circuit breaker at bus 4 connecting the

synchronous generator (SG) to the bus was opened

at 1s to disconnect the SG from the power system.

The results are shown in figure 13. A loss of line

causes a surge in the system frequency at the PCC,

this caused a reduction of active power to the

network by the WF to restore the frequency to the

prefault value. The 20kV, 50km line has a severe

impact compared to the 400kV, 100km line due to

close proximity to the WF. At the instant the SG

(generation) was lost; a sudden dip in the system

frequency was experienced, this in turn resulted into

an instant injection of active power from the WF to

the grid to restore the system frequency. The

terminal voltage reduces from the prefault value of

0.655kV to a new value of 0.638kV, 0.641kV and

0.650kV for the loss of 50km line, 100km line and

SG respectively as a result of change in the system

configuration.

Figure 13: Response to loss of transmission line.

5 CONCLUSIONS

The behaviour of wind farm consisting of DFIG in

response to different disturbance emanating from the

power system has been studied. From the study, the

effect of the rotor controller on the stability of a

wind farm has been shown to be significant to the

stability of the wind farm following a disturbance.

Without controller, prefault condition was achieved

after about 3s. With controller, the prefault condition

was achieved almost immediately.

The type of fault on the power system has

different significant impact on the behaviour of the

wind farm with three phase fault being the most

severe fault. The location of the fault occurence is

seen to have little effect on the wind farm. However

the location of fault occurence has significant effect

on the frequency and the voltage at the PCC.

The inertia of wind generators has influence on

the response of the WF to a disturbance. The larger

the inertia the lesser the magnitude of oscillation of

the generator speed. A larger inertia enhances good

stability. The WF responds to the sudden loss of

transmission line and generation in such a way as to

restore the system frequency. The rotor current and

the terminal voltage assume a new value due to the

change in the network configuration.

This paper is useful to the ultility operators in

understanding the probable response of a wind farm

during disturbance in the power system.However, a

qualitative study mainly is carried out on a small test

system. Further investigation is necessary for a large

power system.

0 1 2 3

1.1

1.15

1.2

1.25

1.3

(a) Time (s)

DFIG Speed (pu)

0 1 2 3

-0.8

-0.6

-0.4

-0.2

0.2

(b) Time (s)

Active power (pu)

0 1 2 3

-0.5

0.5

Electrical torque (pu)

0 1 2 3

0.2

0.4

0.6

0.8

(d) Time (s)

Term inal voltage (kV)

50kgm

100kgm

150kgm

200kgm

0 1 2 3

-0.72

-0.7

-0.68

-0.66

-0.64

Time (s)

Active power (pu)

0 1 2 3

0.63

0.64

0.65

0.66

Time (s)

Terminal voltage (kV)

0 1 2 3

49.95

50.05

50.1

50.15

Time (s)

Frequency at (Hz)

0 1 2 3

0.76

0.78

0.8

0.82

Time (s)

Rotor current (pu)

20kV,50km line loss 400kV,100km line loss SG loss

STUDY OF WIND FARM BEHAVIOUR DURING POWER SYSTEM NETWORK DISTURBANCE

247

REFERENCES

Arifujjaman, M. D., M. T. Iqbal, et al. (2009). Vector

Control of a DFIG Based Wind Turbine, "Journal Of

Electrical & Electronics Engineering." 9(2):1057-1066.

Conroy, J. and R. Watson (2009). "Aggregate Modelling

of Wind Farms Containing Full-Converter Wind

Turbine Generators with Permanent Magnet

Synchronous Machines: Transient Stability Studies."

IET Renewable Power Generation 3(1): 39-52.

El-Sattar, A. A., N. H. Saad, et al. (2008). "Dynamic

Response of Doubly Fed Induction Generator Variable

Speed Wind Turbine Under Fault." Electric Power

Systems Research 78: 1240-1246.

El-Sayed, M. A. (2010). Integrating Wind Energy into

Weak Power Grid Using Fuzzy Controlled TSC

Compensator. International Conference on Renewable

Energies and Power Quality (ICREPQ,

2010),

Granada, Spain.

El-Sayed, M. A. and M. S. Adel (2010). Wind Energy-

Grid Stabilization using a Dynamic Filter

Compensator. International Conference on Renewable

and Power Quality (ICRPQ 2010), Spain.

Eping, C., J. Stenzel, et al. (2005). Impact of Large Scale

Wind Power on Power System Stability. 5th

International Workshop on Large-Scale Integration of

Wind Power and Transmission Networks for Offshore

Wind Farms, Glasgow, Scoland.

Folly, K. A. and S. Sheetekela (2009). Impact of fixed and

variable speed wind generators on the transient

stability of a power system network. Power Systems

Conference and Exposition, 2009. PSCE '09.

IEEE/PES.

Krause, P. C., O.Wasynczuk, et al., Eds. (2002). Analysis

of Electric Machinery and Drive Systems Second

Edition, A John Wiley and Sons,Inc.Publication.

Lipo, T. A. (2000). Electric Machine Analysis and

Simulation. Research Report. W. E. M. a. P. E.

Consortium. Madison, Wisconsin Power Electronic

Research Center, University of Wisconsin-Madison.

Naimi, D. and T. Bouktir (2008). "Impact of Wind Power

on the Angular Stability of a Power System."

Leonardo Electronic Journal of Practices and

Technologies 12: 83-94.

Poller, M. A. (2009). Doubly_FEd Induction Machine

Models for Stability Assessment of Wind Farms,

http://www.digsilent.de/consulting/publication/DFIG

modelling date accesed, 28th Sept.

Slootweg, J. G., S. W. H. de Haan, et al. (2001). Modeling

wind turbines in power system dynamics simulations.

Power Engineering Society Summer Meeting, 2001.

IEEE.

Soares, O. M., H. N. Gocalves, et al. (2009). Analysis and

NN-Based Control of Doubly Fed Induction Generator

in Wind Power Generation. International Conference

on Renewable Energies and Power Quality

(ICREPQ

2009), Valencia(Spain).

Veganzones, C., S. Martinez, et al. (2005). Large Scale

Integration of Wind Energy into Power Systems.

Electrical Power Quality and Utilisation, Magazine.

Spain. 1: 15-22.

Xing, Z., Q. Zheng, et al. (2005). "Integration of Large

Double-Fed Wind Power Generator System into Grid."

8th international Conference on Electrical Machines

and System.: 1000-1004.

APPENDIX

TABLE: DFIG Parameters.

Description Values

Active power ,P 2MW

Rated voltage 0.69kV

Stator resistance Rs 0.01pu

Stator reactance, Xs 0.1pu

Rotor resiatance, Rr 0.01pu

Rotor reactance, Xr 0.1pu

Magnetizing reactance,Xm 3.5pu

Inertia 75Kgm

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

248