COMPARATIVE STUDY OF PROPORTIONAL INTEGRAL
AND PASSIVITY BASED CONTROL FOR BUCK CONVERTER
S. Ganesh Kumar and S. Hosimin Thilagar
DEEE, Anna University Chennai, 600025, Tamilnadu, India
Keywords: Buck converter, Passivity based control, Proportional-integral controller.
Abstract: Passivity Based Controller (PBC) is said to be following energy shaping approach for the faster stabilisation
of output response for the given system. In this paper the PBC is implemented in a buck converter fed D.C.
drive system. The drive is tested for desired speed requirements with constant and step change in load
torque conditions. MATLAB-Simulink is used for simulating the drive system with PBC. The simulated
results confirm that the dynamic response of the PBC is much faster in achieving the desired voltage and
speed when compared with conventional PI controller.
1 INTRODUCTION
Energy is one of the fundamental concepts in
science and engineering practice, where it is
common to view dynamical systems as energy-
transformation devices (Ortega et al., 2001). This
perspective is particularly useful in studying
complex nonlinear systems by decomposing them
into simpler subsystems that, upon interconnection,
add up their energies to determine the full system’s
behaviour. This “energy-shaping” approach is the
essence of Passivity-Based Control (PBC) technique
which is very well known in mechanical systems
(Ortega et al., 2000).
Passivity based controllers for power electronic
circuits are usually synthesized with a stabilization
objective in mind, i.e., to achieve a constant output
voltage or a constant current in the circuit branches.
In this context Euler Lagrange equations were used
earlier for deriving PBC (Ortega et al., 1998) in
various power electronic circuits and also in some
mechanical systems. A unified frame work for the
control of various DC motor configurations using
PBC was derived (Campos-Delgado et al., 2007) in
such a way that the non linear terms in the torque
equations are eliminated. Fundamental equations are
derived for the switching function using PBC
(Hebertt Sira-Ramirez, 2005.) so that the tracking
error can be stabilised to zero. This method is
utilised in this paper for deriving the control
function of Buck converter fed PMDC motor.
PI Controller (PIC) is implemented for a dc
motor drive with inner and outer control loops (P. C.
Sen, 1975). PIC for buck converter fed DC motor is
derived with (Ned Mohan, 2002; Krishnan, 2001)
two control loops.
Transient performances of PBC and PIC were
compared for the H bridge resonant converters (Y.
Lu et al.). It has also been proved that the
stabilisation performances of PBC is superior to that
of PIC for the case of H bridge multi level converter
(A. Dell Aquila et al., 2002)
In the present paper PBC is used for buck
converter fed PMDC motor and its performance is
compared with conventional PIC. The comparison of
the behaviour of the two schemes has been solely on
the transient and steady state response for constant
load torque and step change in load torque.
This paper is organised as follows: Passivity
Based Control theory is presented in Section 2. The
Section 3 is devoted for the Implementation of PBC.
Section 4 describes the simulation results and the
comparative study of two controllers. The
conclusions and the future scope for the work are
given in section 5.
2 PASSIVITY BASED CONTROL
THEORY
Planning of stabilised trajectories is mandatory in
power electronic converter applications such as
309
Ganesh Kumar S. and Hosimin Thilagar S..
COMPARATIVE STUDY OF PROPORTIONAL INTEGRAL AND PASSIVITY BASED CONTROL FOR BUCK CONVERTER.
DOI: 10.5220/0003577703090314
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
309-314
ISBN: 978-989-8425-78-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Power quality, DC & AC Drives etc. In these
applications feedback regulation is accomplished
through proper control functions. Passivity based
controllers for power electronic circuits are usually
synthesized with a view to achieve a constant output
voltage or a constant current in the circuit branches.
Passivity concept was introduced by Willems
(1972). The motivation for adopting the PBC
approach in this paper is due to the following facts.
1. PBC of dc-dc converters is simple as well as
robust.(Marfa and Hebertt, 1998).
2. In power factor correction applications desired
output voltage with upf at the input side are
possible with PBC and Sliding mode Control
(G. Escobar and, H. Sira, 1998)
3. PBC can be used as a soft starter for DC motor
and it can be implemented for speed control
with out any speed sensor. (J. Linares and H.
Sira, 2004).
4. In the parallel operation of Inverters with non
linear loads proper current sharing between the
inverters as well as sinusoidal output current
can be achieved using PBC.(Gustavo et al.,
2006).
5. Using PBC, exponential stability and high
dynamic performance can be obtained.(Daniel
and Gerardo, 2007).
A study of the linearized models of the dc-to-dc
power converters exhibit a clear “energy
management ” structure. Also the conservative part,
the dissipative part of the system and the energy
acquisition part of the system dynamics are clearly
indicated. Based on Lyapunov stability theory, a
desired time varying trajectory for the linearized
dynamic state is proposed. This results in the need to
inject damping into the desired system dynamics and
to force the incremental energy (energy of the
tracking error system) to be driven to zero by
suitable feedback. For this reason, the method is
better known as the “Energy shaping + Damping
Injection” (ESDI) methodology. It turns out that for
the linearized models of the studied dc-to-dc power
converters, the ESDI method produces simple
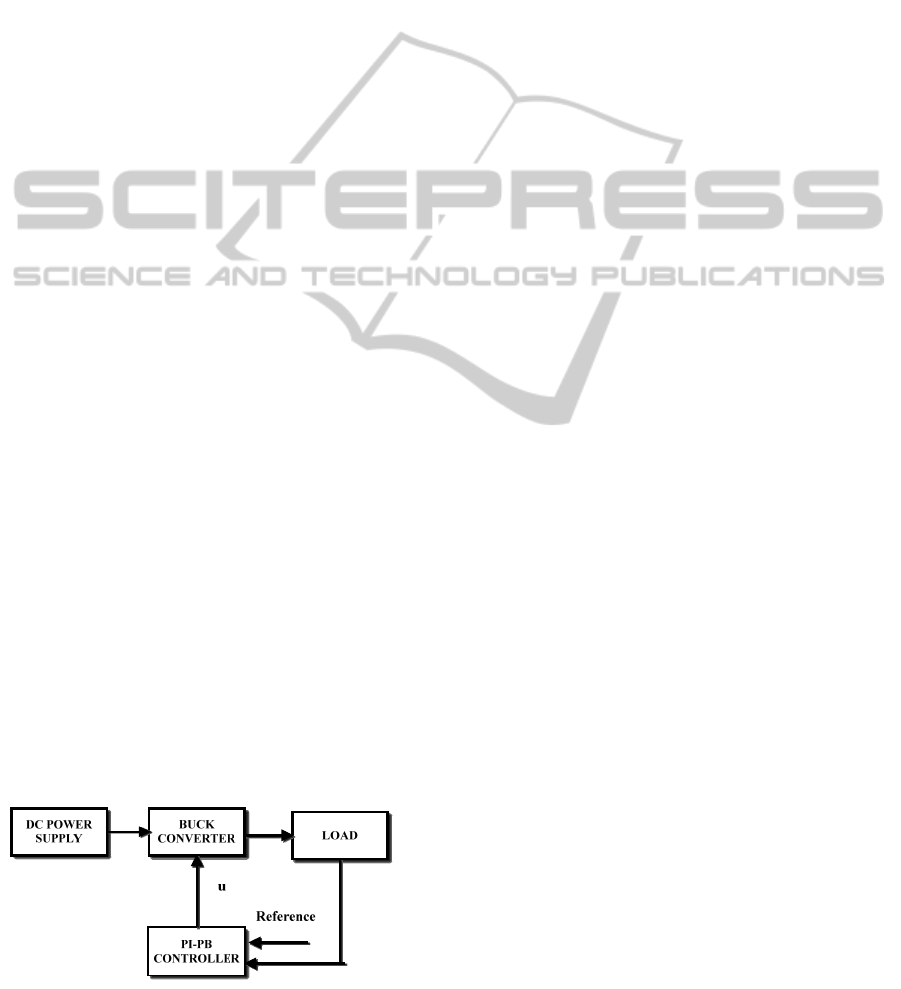
dynamic output feedback controllers. The block
diagram for implementing PBC and PIC is shown in
figure 1.
Figure 1: Block Diagram for Buck Converter with PI/PB
Controllers.
3 IMPLEMENTATION OF PBC
Most of the power electronic converters clearly
exhibit the following structure.
1. Conservative vector field characterised by the
product of skew symmetry matrix with the state
vector. The important property of skew symmetry
matrix is that it does not intervene in the system
stability considerations.
2. A dissipative vector field characterised by the
product of a constant symmetric positive
semidefinite matrix with the state vector.This term
accounts for the dissipative forces in the system
due to resistances and frictions.
3. The control inputs which entitles a constant
matrix multiplying with the input vector. A time
varying or alternatively constant vector field
representing the external forces.Such a general
model is given below.
A (dx/dt) =Jx-Rx+Bu+E; y=B
T
x (1)
where:
x is an n-dimensional state vector,
A is a symmetric, positive definite, constant
matrix
J is a skew symmetric Matrix.
B is a constant n x m matrix
y is an m dimensional output vector.
u is the average control input vector of m
dimension.
E is a n-dimensional smooth vector function of t
or, sometimes, a vector of constant entries.
R represents the dissipative field of the system.
3.1 Procedure for Implementing PBC
To implement PBC the following procedure can be
followed.
1. The state model for the system is obtained.
2. The desired static control function (i.e. u
*
) is
derived by setting dx/dt = 0.
3. The dissipation injection term is introduced in
the calculated error state variables (i.e. [x-x
*
])
multiplied with the input matrix B
T
.
4. The difference in Energy Function ‘V’ for the
state variable(x) and the desired state
variable(x
*
) is calculated.
5. With the derived feedback control function (2),
dV/dt is found and it is verified whether dV/dt
is negative definite or not.
6. If it is so, then the tracking error vector
e (t) = x (t) – x*(t) is stabilized to zero when
the following linear time-varying tracking error
feedback controller is used.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
310

u=u
*
- ґ [B (t)]
T
e (2)
Where
Γ- Diagonal matrix with Dissipation terms,
e- Error between desired value of state variable and
instantaneous value of state variable.
3.2 Modelling of Buck Converter Fed
PMDC Motor
A Buck converter fed PMDC motor is a circuit
constituted of power electronic components with
PMDC motor connected as shown Fig 2. The
variation of u determines the value of output
voltagev of the converter as well as the speed of the
motor.
The state space model for Buck converter fed
PMDC motor is given below:
dx
1
/dt = (k/J)x
2
- (f/J)x
1
-(T
L
/J) (3)
dx
2
/dt = (R
m
/L
m
)x
2
- (k/L
m
)x
1
- ( x
3
/L
m
) (4)
dx
3
/dt = (1/C)x
4
- (1/C)x
2
(5)
dx
4
/dt = (uE/L)-(1/L)x
3
(6)
Where x
1
, x
2
, x
3
and x
4
represent the average
values of the angular velocity ω, the dc motor
armature current i
a
, the converter output voltage v
and the converter inductor current i, respectively .
The state matrix (A
1
) and Input matrix (B) are given
below.
A
1
=[-f/J k/J 0 0;-k/L
m
R
m
/L
m
-1/L
m
0;
0 0 -1/C 1/C ; 0 0 -1/L 0];B
T
= [0 0 0 E/L]
Figure 2: Buck Converter Circuit with Motor Load.
3.3 Passivity based Control for Buck
Converter Fed PMDC Motor
In this section the various steps to be adopted in the
implementation of PBC based Buck converter fed
PMDC motor are discussed as follows. .
In the first step the static duty cycle is found by
equating dx/dt =0 which gives u
*
=v
*
/E. Then in step
two u
*
, ґ,(x-x
*
),B
T
are substituted in (2).Then the
expression obtained is
u= (v
*
/E) – ґ [i-(v
*
/R)]*(E/L) (7)
Where v
*
- Desired Voltage
ґ - Damping Injection coefficient
4 SIMULATION RESULTS
The buck converter fed PMDC motor is simulated in
MATLAB Simulink with the specification of the
parameters given below.
L=20 mH
C=400 μF
k=0.046
J=7.06e-5 kg*m
2
f=8.42e-4 N-m/rad
L
m
=2.63 mH
R

=2.0 ohm
E=12 V
T
L
=Varying from 0.05 to 0.1N-m at one second,
ω
d
= Speed Reference 50, 25 &75rad /Sec
K
p
=0.0072,K
i
=0.1.
For the sake of comparison both PIC &PBC are
implemented in buck converter fed PMDC motor
and the corresponding simulated results are shown in
figure 3 and figure 4 respectively.
Figure 3 indicates the speed, armature current
and Torque responses of Buck converter fed PMDC
motor with PIC. The following observations have
been made.
1. When the motor started with a constant load
torque of 0.05 Nm ,the starting current rises up
to 2.35A. PIC settles the current to 2A and
speed reaches the desired reference of 50
Rad/Sec after 0.9 seconds.
2. At one second, the load torque is increased to
0.1Nm.When the load torque changes
instantaneously the speed is decreases to 37
Rad/Sec and then settles at 50 Rad/Sec after 0.7
Seconds.This is shown in Figure 3(ii) . During
this operation the current settles at 3.089 A
without overshoot.
3. At two seconds the speed reference is changed
from 50 to 25 Rad/Sec.Due to this change, there
is an undershoot in the current response upto
2.23A and the response settles at 2.63A with
the desired speed of 25 Rad/Second after 0.7
seconds.
COMPARATIVE STUDY OF PROPORTIONAL INTEGRAL AND PASSIVITY BASED CONTROL FOR BUCK
CONVERTER
311

Figure 3(i): Speed Vs Time.
Figure 3(ii): Speed Vs Time(Expanded View around 1Seconds).
Figure 3(iii): Armature Current Vs Time.
Figure 3(iv): Torque Vs Time.
Figure 3: PIC for buck converter with PMDC motor.
Figure 4 represents the speed, armature current
and Torque responses of Buck converter fed PMDC
motor with PBC.
1. When the motor is started with a constant load
torque of 0.05 Nm ,the starting current rises up
to 2.523A.PBC settles the current to 2A and
speed reaches the desired reference of 50
Rad/Sec after 0.5 seconds.
2. At one second the load torque is increased to
0.1Nm.When the load torque changes
instantaneously the speed is decreases to 49.13
Rad/Sec and then settles at 50 Rad/Sec after
0.29 Seconds.This is shown in Figure 4(ii).
During this operation the current rises upto
3.375A and then settles at 3.089 A.
3. At two seconds the speed reference is changed
from 50 to 25 Rad/Sec.Due to this change, there
is an undershoot in the current response upto
2.525A and the response settles at 2.63A with
the desired speed of 25 Rad/Sec after 0.5
seconds.
This shows the dynamic capability of PBC i.e. it
can stabilise the current with less time, even though
the overshoots and undershoots occur in the current
response.
So it may be concluded that PBC settles the
speed of buck converter fed PMDC motor with 0.5
seconds for various speed references and constant
load torque of 0.05 Nm. When the load torque is
changed from 0.05 to 0.1 Nm there is less
undershoot in the speed and it settles at the desired
speed after 0.29 Seconds. But in the case of PIC,
settling time was 0.9 seconds for the speed reference
of 50 Rad/ Sec with the applied load torque of 0.05
Nm and the settling time for step change in load
torque to 0.1 Nm is 0.7 seconds. When there is a
decrease in speed reference from 50 to 25 Rad / Sec,
PIC settles the speed to 25 Rad/Second after 0.7
Seconds.
Table 2 indicates the performances of both PIC
and PBC for Buck Converter fed PMDC motor with
various speed references (
ω
d
) with and without step
change in load torque (T
L
).The comparative analysis
of PBC and PIC is done for the change of speed
reference made at zero, two and three seconds with
constant load torque of 0.05 Nm. Also the
performances are analysed with the change of load
torque (0.1 Nm) made at one second. From the
tabulated results it is concluded that PBC performs
faster than PIC.
0 1 2 3 4 5
-10
0
10
20
30
40
50
60
70
80
TIME(SECOND)
SPEED
(RAD/SEC)
0.2 0.4 0.6 0.8 1 1.2 1.4
30
35
40
45
50
TIME(SECOND)
SPEED
(RAD/SEC)
0 1 2 3 4 5
0
1
2
3
4
5
TIME(S)
ARMATURE
CURRENT(A)
0 1 2 3 4 5
0
0.05
0.1
0.15
0.2
0.25
TIME(SECOND)
TORQUE(Nm)
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
312

Figure 4(i): Speed Vs Time.
Figure 4(ii): Speed Vs Time (Expanded View around 1Sec).
Figure 4(iii): Armature Current Vs Time.
Figure 4(iv): Torque Vs Time.
Figure 4: PBC for buck converter fed PMDC Motor.
Table 2: Comparison between PIC and PBC.
S.No
Time
Duration
(Sec.)
T
L
(Nm)
ω
d
(Rad/Sec)
Settling
Time(Sec.)
PBC
PIC
1.
0-1 0.05 50 0.5 0.9
2.
1-2 0.1 50 0.29 0.7
3.
2-3 0.1 25 0.5 0.7
4.
3-5 0.1 75 0.5 0.7
5 CONCLUSIONS
In this paper the performance of PBC based buck
converter fed dc drive system has been simulated
and studied. The study shows that PBC facilitates
the drive response to settle faster as against the PIC
without any speed sensor. Since the performance of
PBC in electric drive application is found to be very
promising it can be applied for other drive system
also. Both the controllers are being tested
experimentally for their robustness and dynamic
performance.
REFERENCES
J. C. Willem, 1972 Dissipative dynamical Systems-Part I;
General Theory In: Journal of Archeieve for Rational
Mechanics and Analysis, 45(5):321-351
P. C. Sen 1975 Thyristor D C Drives In John Wiley and
sons
Ortega R, Loria A, Nicklasson H, Sira-Ramirez H 1998
.Passivity based control of Euler-Lagrange systems:
mechanical, electrical & electromechanical
applications. In: Springer, London .
Marfa Isabel Angulo-Nunez and Hebertt Sira –Ramirez
1998 Flatness in the Passivity Based Control of DC-
DC Power Converters In: IEEE Proceedings pp 4115-
4120.
G. Escobar, H. Sira Ramirez 1998 A Passivity based –
Sliding Mode Control Approach
Romeo Ortega, Arjan J. van der Schaft, Iven Mareels and
Bernhard Maschke.September 25-27, 2000 Energy
Shaping Revisited In: IEEE Proceedings on
International Conference on Control Applications pp
121-126
Romeo Ortega, Arjan J. van der Schaft, Iven Mareels, and
Bernhard Maschke .April 2001 Putting Energy Back
in Control In: IEEE Control Systems Magazine.
Krishnan R. 2001. Electric Motor Drives –Modelling
Analysis and Control In: PHI India
Ned Mohan, 2002. A first Course on Power Electronics
and Drives In: MNPERE.
A. Dell Aquila, V. G. Monopoli, M. Liserre 2002. Control
of H-Bridge Based Multilevel Converters In: IEEE
Proceedings pp 766-771.
0 1 2 3 4 5
0
20
40
60
80
100
TIME(SECOND)
SPEED(RAD/SEC)
0.94 0.96 0.98 1 1.02 1.04 1.06 1.08
48
48.5
49
49.5
50
50.5
TIME(SECOND)
SPEED(RAD/SEC)
0 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
4
TIME(SECOND)
ARMATURE
CURRENT(A)
0 1 2 3 4 5
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
TIME(SECOND)
TORQUE(Nm)
COMPARATIVE STUDY OF PROPORTIONAL INTEGRAL AND PASSIVITY BASED CONTROL FOR BUCK
CONVERTER
313

J. Linares-Flores, H. Sira Ramirez 2004 DC motor
velocity control through a DC-DC power Converter
In: IEEE Proceedings pp 5297-5302.
Hebertt Sira-Ramirez 2005. Are nonlinear controllers
really necessary in power electronics devices? In: EPE
2005.
Hebertt Sira-Ramírez and Ramón Silva-Ortigoza 2006.
Control Design Techniques in Power Electronics
Devices In: Springer, London .
Gustavo Perez-Ladron, Victor Cardenas ,Gerardo
Espinosa 2006 Analysis and Implementation of a
Master –Slave Control based on a Passivity Approach
for Parallel Inverters Operation In: IEEE Proceedings
CIEP Mexico October 16-18.
Campos-Delgado. D. U, Palacios. E, Espinoza –Trejo D.
R. 2007. Passivity Based Control of Nonlinear D. C.
Motors Configurations and Sensor less Applications
In: IEEE Proceedings pp 3379-3384.
Daniel Noriega-Pineda, Gerardo Espinosa-Perez
2007.Passivity Base control of Multilevel Cascade
Inverters: High performance with Reduced Switching
Frequency In: IEEE Proceedings pp3403-3408
M. Baja, D. Patino, H. Cormerais, P. Riedinger and J.
Buisson 2007 Hybrid Control of a three-level three-
cell dc-dc converter In : IEEE Proceedings pp 5458-
5463.
Y. Lu, K. W. E.Cheng, S. L. Ho, J. F. Pan, Examination of
H-Bridge Resonant Converter using Passivity Based
Control In : Journal IEEE
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
314