KINETICS MODELING OF WOOD TORREFACTION
Weight Loss Kinetics
A. Pétrissans, M. Chaouch, P. Gérardin, M. Pétrissans
LERMAB, Université Nancy I, BP 70239, 54506, Vandoeuvre les Nancy, France
R. Younsi
Département de Génie Mécanique, École Polytechnique de Montréal, Montréal (Qc), H3C 3A7, Canada
Keywords: Heat treatment, Modelling, Reaction kinetics, Thermo-degradation, Wood.
Abstract: Torrefaction is a thermal treatment step in a relatively low temperature range of 210–240˚C, which aims to
improve the dimensional stability and durability of wood. The weight loss kinetics for torrefaction of wood
samples was studied using equipment specially conceived to measure mass losses during thermal treatment.
Laboratory experiments were performed under nitrogen for heating rates of 1˚C.min
-1
. A mathematical
model for the kinetics of the thermodegradation process was used and validated. Measurements of
temperature distribution and anhydrous weight loss were performed on dry sample of poplar wood during
pyrolysis in an inert atmosphere at 230°C. The mathematical formulation describing the simultaneous heat
and mass transfers requires coupled nonlinear partial differential equations. These unsteady-state
mathematical model equations were solved numerically by the commercial package FEMLAB. A detailed
discussion of the computational model and the solution algorithm is given. Once the validity of different
assumptions of the model had been analyzed, the experimental results were compared with those calculated
by the model. Acceptable agreement was achieved.
1 INTRODUCTION
Nowadays the use of wood as building material is
promoted. The heat treatment of the wood by mild
pyrolysis is used to improve some of the
characteristics of the final wood product, such as its
durability and dimensional stability. This process
substitutes the use of external chemical products,
which enables the treated wood to remain an
environmentally friendly product. It’s an effective
method to improve biological durability of wood
(Shi et al. 2007). The heat treatment of the wood
induces a chemical modification of the main wood
constituents. The lignin polymer structure is
modified, the ratio between the amorphous and the
crystalline cellulose is also changed, hemicelluloses
are strongly decomposed (Sinoven et al., 2002,
Nguila et al., 2006, Nguila et al., 2007a, Gérardin et
al., 2007), some products precursors of the charcoal
appear (Nguila et al., 2007b). These chemical
modifications confer with the new wood properties
as the improved dimensional stability (Mouras et al.,
2002, Esteves et al., 2007), the improved fungal
resistance (Kamdem et al., 2002, Hakkou et al.,
2006).
The concept of thermal treatment to stabilise the
wood structure has lead to the development of
several treatment processes in some European
countries. In the 70s, the research developed by the
Ecole des Mines de Saint-Étienne (France) has
worked out for the first time an industrial process
named «Retified wood®». More recently, in the 90s,
the forest industry in Finland has developed a new
process; Thermowood®. Some others technologies
have been developed such as the Netherlands
process «PLATO® » and the Menz Holz’s process
OHT in Germany. The wood torrefaction is a heat
treatment of ligno-cellulosic material carried out at
temperatures up to 300 °C. Torrefaction can be
carried out under different gaseous atmospheres.
Nitrogen or hot gases released during the thermal
treatment are employed most of time. Chemical
reactions involved during torrefaction as well as
final properties of the material depend strongly on
116
Pétrissans A., Chaouch M., Gérardin P., Pétrissans M. and Younsi R..
KINETICS MODELING OF WOOD TORREFACTION - Weight Loss Kinetics.
DOI: 10.5220/0003578101160121
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
116-121
ISBN: 978-989-8425-78-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the treatment temperature and the duration of the
process. During torrefaction, slow pyrolysis prevails:
wood is thermally decomposed at a slow rate
(Degroot et al., 1988). The anhydrous weight loss
(AWL) resulting from the wood decomposition is
representative for physical-chemical transformations
of wood. The AWL matches to the advancement of
the torrefaction process.
According to the treatment intensity, the
conferred properties of the wood vary strongly. For
high values of the treatment temperature and time,
the fungal resistance becomes total. Recent studies
have shown the direct relation between the
anhydrous weight loss (AWL) due to thermo-
degradation and the conferred wood properties
(Hakkou et al., 2005, Welzbacher and Brischke,
2007). Hence, controlling the heat treatment process
means to control precisely the AWL of the material.
It requires a coupled model taking into account heat
transfer and mass transfer due to thermo-degradation
reactions inside wood sample.
The mechanism of wood thermo-degradation
shows the presence of several phases when the
temperature increases. A phase of elimination of
some volatile compounds takes place at
temperatures lower than 200°C. For temperature
range of 200–280°C, hemicelluloses are converted
essentially into gases and acetic acid. This step
corresponds to the wood roasting.
At the temperature range about 250-300°C, the
lignin and cellulose decompose to give three
products: gas, tar and char. This decomposition leads
to an anhydrous weight loss, representative for wood
chemical transformation. Properties of heat-treated
wood depend on the mass losses (Nguila et al.,
2009). Hence, controlling the quality of the heat
treated wood means to control precisely mass loss
during the treatment. Therefore, the knowledge of
the kinetic schemes of the wood thermo-degradation
is required.
The aim of this study is to develop a tool
allowing predicting the temperature profiles in the
wood and the associated AWL during the treatment.
A two-stage semi-global kinetic model is used here
to describe the wood thermo-degradation. Numerous
experiences of heat treatment at 240°C under
nitrogen were realized with five wood species. The
curves of the instantaneous mass loss and
temperature were recorded. The experimental data
were used to determine the model parameters.
Finally, a comparison between the experimental data
and the numerical results was realized.
2 MATERIAL AND METHODS
Heat treatment is carried out on wood panels of large
sections, dried in the steam room at 105°C until their
mass stabilization. The panel’s dimensions are 25 x
11 x 2.5 cm3 respectively in the longitudinal,
tangent and radial directions. The wood specie used
in the present study has the Poplar (Populus nigra).
Heat treatment has been carried out under
nitrogen by conduction between two metallic
heating plates placed on a precision balance. The
instantaneous weight and temperatures at the surface
and in the middle of the sample are recorded. The
heat treatment phase consists of three successive
thermal stability areas. The firs one is kept at 105°C
in order to verify the mass stability (anhydrous
mass). The second one (165°C) is useful for the
thermal homogenization of the panel. The last one
corresponds on the thermo-degradation operating
temperature.
3 MATHEMATICAL
FORMULATION
Wood is a complex material whose thermo-
degradation involves series of chemical reactions
with coupled heat and mass transfer. This section is
devoted to the mathematical formulation of the
mentioned transfers in the wood porous media
introducing as well the heat effects due to the
reactions of polymer decomposition, as the obtaining
of volatiles and non-degradable solid products. The
following simplifying assumptions are used for the
mathematical formulation:
- the wood sample has a rectangular form
characterised by its length L, width l and thickness e,
respectively in the longitudinal, tangent and radial
directions. The sample thickness is very weak
compared to the other dimension and the modelling
can be represented in 1D.
- the convection transfer occurring because of the
formation of volatiles inside the wood material
during the heat treatment is neglected.
- the dimensions of the sample are considered
invariable; the formation of fissures and cracks is
neglected.
- the wood physical and thermal properties
respectively the specific heat Cp and the wood
thermal conductivity
λ are considered as a linear
function of the temperature.
()
27385.41112 −
+
=
TCp
(1)
KINETICS MODELING OF WOOD TORREFACTION - Weight Loss Kinetics
117

() 2730003.013.0 −+= T λ
(2)
The macroscopic conservation equation governing
the heat transfer phenomenon is given by:
t
Hp
x
T
xt
T
Cp
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
ρ
λρ
(3)
where: Vtm )(=
ρ
is the averaged anhydrous wood
density, T is the local temperature, Hp is reaction
enthalpy. The instantaneous sample weight m(t) is
detailed after on by the Eq. (11), the sample volume
V is considered invariable.
The process of the wood heat treatment involves
several reactions that of polymer degradation and
synthesis giving numerous reaction products
(Weiland et al., 1998, Nguila et al., 2009).
Consequently, mathematical modelling describing
the wood thermo-degradation is a simplified
approximation of the real phenomena. However, the
knowledge of kinetic schemes describing the
thermo-degradation process is required for
elaboration of predicting tools allowing the control
of wood heat treatment.
Numerous mechanisms have been published to
provide a rational explanation of the wood thermo-
degradation and the associated heat effects. Three
main approaches could be distinguished: the first
one considers the wood as a single homogeneous
element (Di Blasi and Branca, 2001, Rath et al.
2003, Sadhukhan et al., 2008), the second one takes
into account the decomposition of the essential wood
compounds: cellulose, hemicelluloses and lignin
(Rousset et al., 2006), the third one considers the
existence of three fractions (pseudo-compounds)
which decomposition obeys different lows (Grioui et
al., 2006). It is usually assumed that the reaction
kinetics follows an Arrhenius low with two
parameters: activation energy and kinetic constant.
The mechanisms adopted in this work, is based
on a two-stage, semi-global multi-reaction kinetic
model of wood mild pyrolysis where the wood is
subdivided into three pseudo-components A
1
, A
2
, A
3
,
as it was previously proposed by Grioui et al.
(2006). Each pseudo-component is characterised by
a specific kinetic law of decomposition and its mass
fraction, respectively
α
1
, α
2
and α
3
, such as α
3
= 1 -
α
1
+ α
2
. At a temperature level lower than 200°C
occurs the elimination of some volatile wood
compounds. At the temperature range 165 to 240 °C,
the degradation of A
1
prevails giving a gaseous
product G
1
. The thermo-degradation of A
2
leads to
the production of a solid fraction C
2
and a gas
product G
2
. The proposed kinetic scheme is given by
the Eq. (4-5):
11
1
GA
k
⎯⎯→⎯
(4)
()
22222
1
2
GCA
k
γγ −+⎯⎯→⎯
(5)
The mass fractions of the non-degradable solid γ
2
and
γ
3
depend on the temperature.
The assumption that the kinetic of all the
involved reactions is described by first order laws
the mass balance equations can be written
respectively as follows:
1
1
1
td
d
A
A
mk
m
−=
(6)
2
2
2
td
d
A
A
mk
m
−=
(7)
2
2
22
td
d
A
C
mk
m
γ =
(8)
where
1
A
m ,
2
A
m and
2
C
m are respectively the mass
of the constituents A
1
, A
2
and C
2
; k
1
and k
2
are the
reaction rate constants obeying the Arrhenius low
such as :
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
TR
Ea
kk
1
011
exp
(9)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
TR
Ea
kk
2
022
exp
(10)
where, k
01
and k
02
are the pre-exponential factors;
Ea
1
and Ea
2
are the activation energies. The
instantaneous total mass of the sample is equal to:
)()()()()(
232
tmtmtmtmtm
CAAA
A
+++=
(11)
The resolution of the Eq. (3-10) requires the
determination of 8 parameters: the pre-exponential
factors k
01
, k
02
, and activation energies Ea
1
, Ea
2
, the
mass fraction fractions
α
1
, α
2
and γ
2
; the reaction
enthalpy Hp. These parameters have been obtained
by minimizing an error function between the
experimental data and simulation results. The
number of parameters to determine is large and the
optimization procedure becomes difficult. The error
function to minimize over both thermal and mass
measurements is given be the Eq. (12):
()
()
∑
∑
=
=
+
−
+
+
+
−
=
2
1
1
exp
exp
2
1
exp
exp
1
)()(
)()(2
1
)()(
)()(2
1
n
j
calculated
calculated
n
i
calculated
calculated
jMLjML
jMLjML
n
iTiT
iTiT
n
error
(12)
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
118

where n
1
is the number of data points of the
temperature, T
exp
(i) is the experimental temperature,
T
calculated
(i) is the calculated temperature on the i-th
grid point, n
2
is the number of data points of the
mass loss ML
exp
(j) and ML
calculated
(j) are respectively
the experimental and the calculated mass loss due to
the thermo-degradation on the j-th grid point. The
anhydrous mass lost is defined as follows:
()
00
)( mtmmAML −=
(13)
m
0
is the anhydrous wood weight before heat
treatment.
The experiences are carried out in such a way,
allowing the determination of the model parameters
over two stages. At the first isothermal area at
165°C, the reaction giving by the Eq. (5) can be
neglected because of its very slow rate. It has been
also considered that the reaction enthalpy of the first
reaction is negligible. The three parameters relative
to the first reaction (Eq. 4) are then determined:
α
1
,
k
01
and Ea
1
. The second isothermal area at 230°C,
corresponding to the heat treatment process, allows
the determination of the five other parameters:
α
2
,
γ
2
, k
02
, Ea
2
and Hp. A random algorithm has been
used, and the minimum and maximum values of
each parameter have been initialised according to the
values available in the literature (Di Blasi and
Lanzetta, 1997, Grioui et al., 2006, Rousset et al.,
2006).
The governing equations are solved numerically
with the commercial package, FEMLAB (Cosmol,
2000). This is designed to simulate systems of
coupled non-linear and time dependent partial
differential equations (PDE) in one-, two- or three-
dimensions. The mesh convergence was verified
with refined mesh sizes. Time step of 360 s, 1866
nodes and 8080 elements mesh size were considered
to be appropriate. The kinetic parameters obtained
using the method described are in Table 1.
Table 1: Kinetic parameters used in the numerical
simulation for the poplar.
α
1
0.08
α
2
0.12
E
a1
(kJ.mol
-1
) 118.5
E
a2
(kJ.mol
-1
) 119.0
k
01
(s
-1
) 4.10
7
k
02
(s
-1
) 6.10
8
γ
0.07
H
p
(kJ.mol
-1
) 123.0
4 RESULTS AND DISCUSSION
To verify the final prediction of the model, experi-
ences have been carried out using poplar wood
during 20 hours under heat treatment temperature of
230°C. The heat treated rate has been fixed to
1°C.min
-1
. Experimental and numerical results of the
surface et centre temperatures and the averaged
weight loss are shown on Fig. 1-3. It can be
observed that the increase of the treatment
temperature enhances the AML. A good agreement
is observed between the experience and the
numerical simulation.
Figure 1: Time evolution of surface temperature: Poplar
(1°C.min
-1
, T
max
= 230°C).
Figure 2: Time evolution of center temperature: Poplar
(1°C.min
-1
, T
max
= 230°C).
KINETICS MODELING OF WOOD TORREFACTION - Weight Loss Kinetics
119

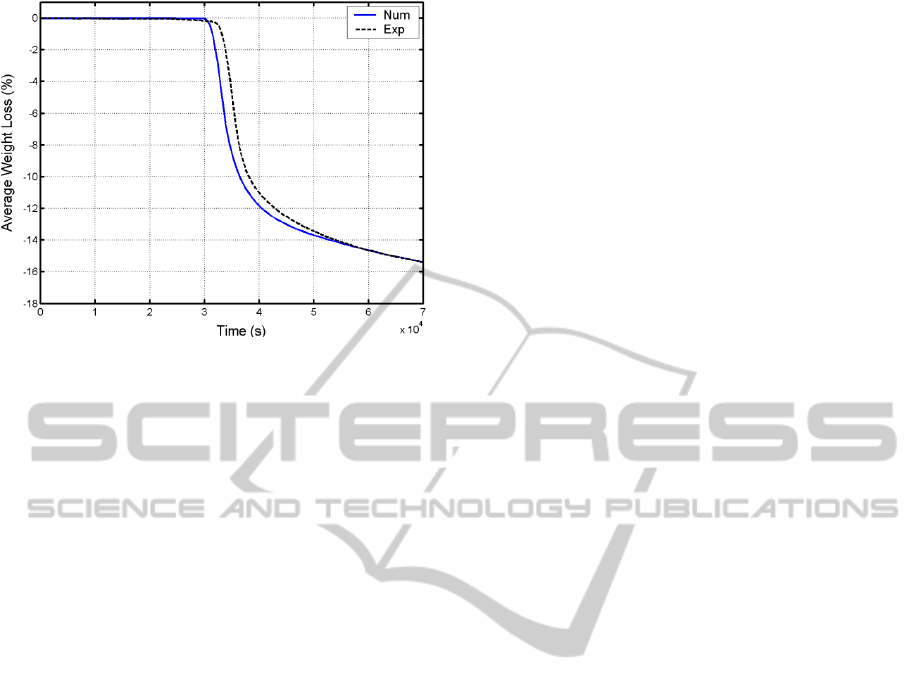
Figure 3: Time evolution of average weight loss: Poplar
(1°C.min
-1
, T
max
= 230°C).
5 CONCLUSIONS
The kinetics for the pyrolysis of wood was
investigated. Based on laboratory experiments
performed with the described device, a mathematical
model for the kinetics of the pyrolysis process was
proposed and validated. This model incorporates the
reaction pathway that was developed by Grioui et al.
(2006) for the description of the transformation of
wood subject to heat. This model allows the
computation of internal profiles of temperature and
average weight loss. The Femlab software was used
to solve the system of partial differential equations.
This work includes a validation section that shows
the ability of the model to accurately predict the
internal profiles of temperature and weight loss in
the experimental configuration. Comparison of the
simulated temperature profiles and average weight
loss with experimentally measured values showed
reasonable agreement.
Further studies may allow accurate modeling of
wood torrefaction mainly by taking into account
thermodgradation of lignin and accurate
thermophysical properties. This model can be used
in the design of industrial pyrolysis installations
REFERENCES
Comsol A. B., Femlab Version 2.0, (2000), Reference
Manual.
Degroot, W. F., Pan, W. P., Rahman, D., Richards, G. N.
(1988) First chemical events in pyrolysis of wood.
Journal of Analytical and Applied Pyrolysis,13 (3)
221–31.
Di Blasi, C., Branca, C. (2001), Kinetics of primary
product formation from wood pyrolysis, Industrial
Engineering Chemistry Research, 40 (23) 5547-5556.
Di Blasi, C., Lanzetta, M. (1997) Intrinsic kinetics of
isothermal xylan degradation in inert atmosphere.
Journal of Analytical and Applied Pyrolysis, 40-41,
287–303.
Esteves, B., Velez Marques, A., Dominigos, I., Pereira, H.
(2007) Influence of steam heating on the properties of
pine (Pinus pinaster) and eucalypt (Eucalyptus
globulus) wood. Wood Science and Technology, 41,
193-207.
Gérardin, P., Petric, M., Pétrissans, M., Erhrardt, J. J.,
Lambert, J. (2007) Evolution of wood surface free
energy after heat treatment. Polymer degradation and
stability, 92 (4), 653-657.
Grioui, N., Halouani, K., Zoulalian, A., Halouani, F.
(2006) Thermogravimetric analysis and kinetics
modeling of isothermal carbonization of olive wood in
inert atmosphere, Thermochimica Acta. 440, 23-30.
Hakkou, M., Pétrissans, M., Gérardin P., Zoulalian, A.
(2005) Investigation of wood wettability changes
during heat treatment on the basis of chemical
analysis. Polymer degradation and stability, 89 (1), 1-
5.
Hakkou, M., Pétrissans, M., Gérardin P., Zoulalian, A.
(2006) Investigations of the reasons for fungal
durability of heat-treated beech wood. Polymer
degradation and stability, 91 (2), 393-397.
Kamdem, D. P., Pizzi, A., Jermannaud, A. (2002),
Durability of heat-treated wood. Holz als Roh-und
Werkstoff, 60, 1-6.
Kocaefe, D., Poncsak, S., Boluk, Y. (2008), Effect of
thermal treatment on the chemical composition and
mechanical properties of birch and aspen. Biores. 3
(2), 517-537.
Mouras, S., Girard, P., Rousset, P., Permadi, P., Dirol, D.,
Labat, G., (2002) Propriétés physiques de bois peu
durables soumis à un traitement de pyrolyse ménagée.
Annals of Forest Sciences 59 (3), 317-326.
Nguila, I. G., Pétrissans, M., Lambert, J. L., Erhardt J. J.,
Gérardin, P. (2006), XPS Characterization of wood
chemical composition after heat treatment. Surface &
Interface Analysis, 38 (10), 1336-1342.
Nguila, I. G., Petrissans, M., Gérardin, P. (2007a)
Chemical reactivity of Heat treated Wood. Wood
Science Technology, 41 (2), 157-168.
Nguila, I. G., Mounguengui, S., Dumarcay, S., Pétrissans,
M., Gérardin, P. (2007b) Evidence of char formation
during wood heat treatment by mild pyrolysis.
Polymer degradation and stability, 92 (6), 997-1002.
Nguila, I. G., Pétrissans, M., Pétrissans, A., Gérardin, P.
(2009) Elemental composition of wood as a potential
marker to evaluate heat treatment intensity.
Polymer
degradation and stability, 94 (3), 365-368.
Rath, J., Wolfinger, M. G., Steiner, G., Krammer, G.,
Barontini, F., Cozzani, V. (2003) Heat of wood
pyrolysis. Fuel, 82 (1), 81-91.
Rousset, P., Turner, Y., Donnot, A., Perré, P. (2006) The
choice of a low-temperature pyrolysis model at the
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
120

microscopic level for use in a macroscopic
formulation, Annals of Forest Science, 63 (2), 213-
229.
Sadhukhan, A. K., Gupta, P., Saha, R. K. (2008)
Modelling and experimental studies on pyrolysis of
biomass particles. Journal of Analytical and Applied
pyrolysis. 81 (2), 183–192.
Shi, J. L., Kocaefe, D., Amburgey, T., Zhang, J. (2007) A
comparative study on brownrot fungus decay and
subterranean termite resistance of thermally-modified
and ACQ-C-treated wood. Holz als Roh- und
Werkstoff, 65 (5), 353–358.
Sivonen, H., Maunu, S. L., Sundholm, F., Jämsä, S.,
Viitaniemi, P. (2002) Magnetic resonance studies of
thermally modified wood. Holzforschung 56 (6), 648-
654.
Weiland, J. J., Guyonnet, R., Gibert, R. (1998) Analysis of
controlled wood burning by combination of
thermogravimetric analysis, differential scanning
calorimetry and Fourier transform infrared
spectroscopy. Journal of Thermal Analysis and
Calorimetry, 51 (1), 265–74.
Welzbacher, C., Brischke, C., Rapp, A. (2007) Influence
of treatment temperature and duration on selected
biological, mechanical, physical and optical properties
of thermally modified wood. Wood Material Science
and Engineering, 2 (2), 66-76.
KINETICS MODELING OF WOOD TORREFACTION - Weight Loss Kinetics
121