CLIMATE-ECONOMY MODELING CONSIDERING SOLAR
RADIATION MANAGEMENT AND ITS TERMINATION RISK
Takanobu Kosugi
College of Policy Science, Ritsumeikan University, 56-1 Toji-in Kitamachi, Kita-ku, Kyoto 603-8577, Japan
Keywords: Climate change, Geoengineering, Global warming, Integrated assessment model, Termination problem.
Abstract: The combination of carbon dioxide (CO
2
) emissions mitigation and geoengineering options of solar radiation
management (SRM) such as placing sunshades in space and stratospheric aerosol injection is discussed
quantitatively using an extended version of the DICE-2007, an integrated assessment model for climate policy
analysis. Though SRM measures can contribute considerably to the cost-effectiveness of climate change
mitigation, they might cause harmful side effects, such as rapid air temperature increases, if the SRM
implementation were to be discontinued for any reason. The author suggests a guideline for the use of SRM:
namely, that unexpected SRM termination at any time would not exceed the constraints on the rate of global
warming recommended by the German Advisory Council on Global Change. The paper describes a method to
incorporate this guideline in the DICE-2007 model, and shows the result of the extended model, which
recommends an 80% reduction of global industrial CO
2
emissions below the 2005 level by the end of the 21st
century while implementing a complementary SRM option to mitigate climate change.
1 INTRODUCTION
Technological measures to mitigate climatic change
include greenhouse gas (GHG) emission reductions
and climate geoengineering options. Among these
measures, solar radiation management (SRM)
technologies such as placing sunshades in space and
injecting sulfur aerosol into the stratosphere have
been evaluated as having relatively large potential to
contribute to the mitigation of climate change (The
Royal Society, 2009).
However, while earlier studies dealing with
strategies of climate change mitigation have focused
on deriving optimal dynamic paths of the GHG
emissions, especially carbon dioxide (CO
2
), few
have additionally considered the timing and scale of
implementing SRM options. Though a pioneering
study by Wigley (2006) shows plausible trajectories
of the combination of CO
2
emissions reduction and
SRM by stratospheric aerosol injection in the future,
it lacks deep discussion of economics and risk
management.
The present study aims at drawing desirable
scenarios based on those combined points of view
by using an integrated assessment model of climate
and economy. For discussing the combination of
CO
2
emissions reduction and SRM, the study pays
special attention to the so-called “termination
problem,” i.e., the risk of adverse effects to climatic
condition accompanied with a rapid global warming
if the use of the SRM option is terminated for any
reason after its implementation.
2 INCORPORATING SRM
OPTIONS IN A
CLIMATE-ECONOMY MODEL
2.1 Modification of the DICE-2007
Integrated Assessment Model
The 2007 version of the DICE model known as an
integrated assessment model of climate change,
DICE-2007 (Nordhaus, 2008), is modified to deal
explicitly with SRM options. The DICE model is
available for public use through its developer’s Web
page and has served as the basis of most other
economic models of climate change.
The model is a nonlinear programming model that
integrates a neoclassical macroeconomic growth
model with the following three models: an emissions
model that computes the amount of CO
2
emissions
315
Kosugi T..
CLIMATE-ECONOMY MODELING CONSIDERING SOLAR RADIATION MANAGEMENT AND ITS TERMINATION RISK.
DOI: 10.5220/0003580003150320
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
315-320
ISBN: 978-989-8425-78-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

caused by economic production and the cost of
mitigating the emissions, a climate model that
simulates the flow and stock of CO
2
in the air and
ocean and their impact on the changes in global
mean atmospheric temperature, and a damage model
that estimates the damage cost caused by a given
rise in air temperature. The objective function is the
total discounted sum of a representative individual’s
instantaneous utility stream. It is a one-region model
that covers the entire world and derives the optimal
dynamic paths of macro investment and CO
2
reduction rate. The total period of time is divided
into 60 time periods, the first of which comprises the
ten years centered on 2005.
Since radiative forcing that determines the
greenhouse effect is controllable only by atmospheric
CO
2
concentration in the DICE model, this study
modifies the model to include SRM options as a
factor controlling radiative forcing, as applied earlier
in Kosugi (2010). The two most important points of
the modification are described as follows.
(i) Either placing sunshades in space or injecting
aerosols into stratosphere is considered to be
applicable. The balance of flow and stock of the sun-
shading materials is modeled; the service life of the
materials, i.e., the period in which the materials stay
in the area effective for SRM, is taken into account
When we define the variables
)(tS
and
)(tG
as
the mass stock of sun-shading materials accumulated
in space or the stratosphere (Mt) and the mass flow
of the materials lifted into space or the stratosphere
(Mt/yr.), respectively, at time period
t
, and the
parameter
S
δ
as the depreciation rate of the sun-
shading materials accumulated in space or the
stratosphere (yr.
-1
), the balance of flow and stock of
sunshades in space is modeled as:
(
)
)1(1)(10)(
10
−−+= tStGtS
S
δ
,
(1)
noticing that a time period consists of ten years in
the DICE model. Given the short staying period of
injected aerosol in the stratosphere of a few years at
the longest, the model for it is as follows:
S
tGtS
δ
)()( =
.
(1’)
(ii) The decrease in radiative forcing by
implementing an option is assumed to be
proportional to the up-mass stock of the sun-shading
material. Letting
)(tF
and
)(tF
EX
be total radiative
forcing and its exogenous part due to non-CO
2
GHGs (W/m
2
relative to 1900) and
)(tM
AT
the
mass of carbon in the atmosphere (GtC), this is
modeled as:
[
]
{
)1750()(log)(
2 ATAT
MtMtF η =
}
)()( tFmtS
EX
+−
,
(2)
where
η
and
m
denote the parameters connecting
radiative forcing with temperature (°C/W/m
2
) and
the sunshade mass-effectiveness coefficient, i.e., the
mass of the stock of sun-shading materials required
to offset the increase in radiative forcing due to a
doubling of the atmospheric CO
2
concentration
(Mt/2×CO
2
), respectively.
By using the calculated radiative forcing, the air
temperature is estimated through the following
simple climate model as in the original DICE model:
{
)1()()1()(
21
−−+−= tTtFtTtT
ATATAT
ξξ
[
]
}
)1()1(
3
−−−− tTtT
LOAT
ξ
,
(3)
[
] )1()1()1()(
4
−−−+−= tTtTtTtT
LOATLOLO
ξ
,
(4)
where variables
)(tT
AT
and
)(tT
LO
represent the
global mean surface temperature and the
temperature of the ocean depths (°C relative to
1900), respectively.
Other modifications include: (iii) the cost of
installing the sun-shading materials is subtracted
from consumption; (iv) CO
2
emissions induced by
installing the sun-shading materials are taken into
account; (v) constraints to avoid an air temperature
drop are imposed; the global mean air temperature is
kept at no less than its 1900 value in the whole
period and the rate of temperature decrease doesn’t
exceed 0.2 °C per decade; and (vi) the CO
2
mitigating trend is assumed to be continued; the rate
of CO
2
mitigation is constrained not to decline with
an elapse of time.
2.2 Assumptions
Among the variety of parameters in the model, the
parameters used in the original DICE model were set
to be the same as the reference values applied in the
DICE-2007. Table 1 (a) shows a major set of
extractions from those parameter settings.
The parameters introduced to incorporate SRM
options in the model are set based on a survey of
literature data (Hertzfeld, et al., 2005; Lenton and
Vaughan, 2009; McClellan et al., 2010; Pearson, et
al., 2006) as shown in Table 1 (b).
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
316

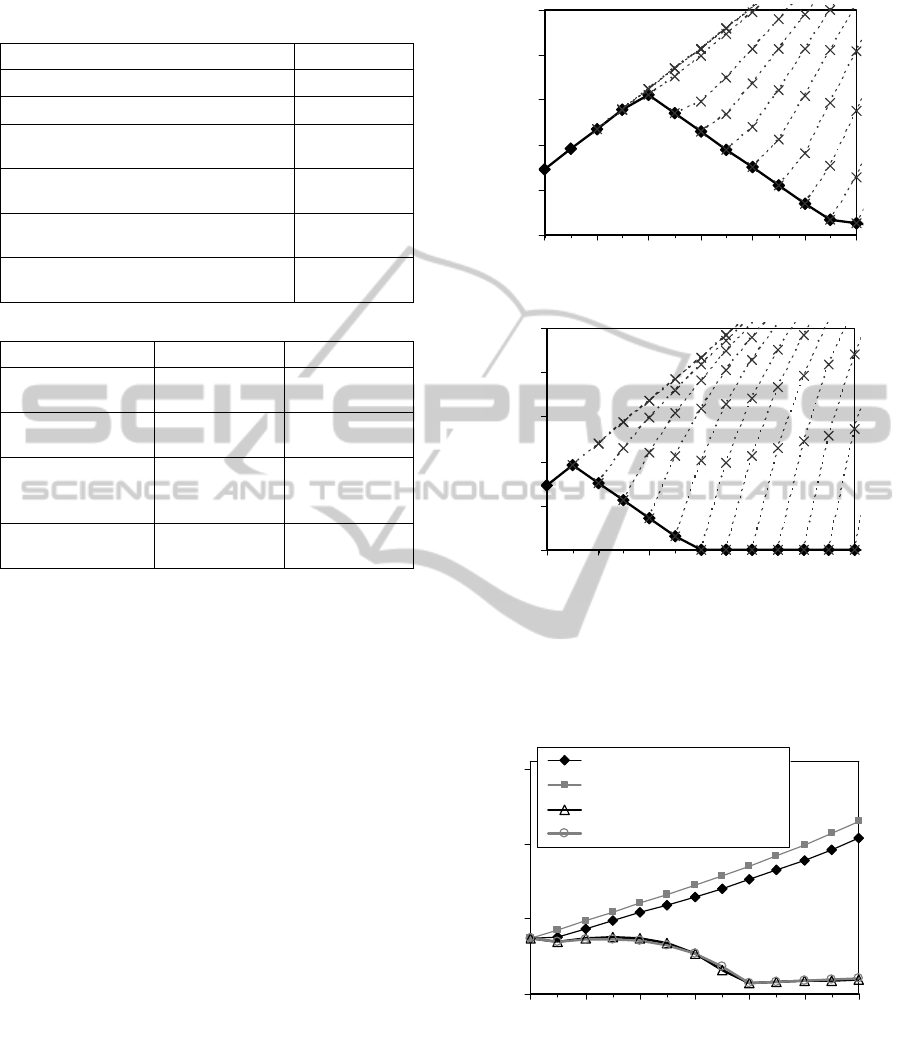
Table 1: Major parameter settings.
(a) Reference values in DICE-2007 model
Parameter Value
Climate sensitivity 3 °C
Social time preference 1.5%/yr.
Elasticity of marginal utility, i.e., relative
risk aversion
2
Initial growth rate of total factor
productivity
0.92%/yr.
Initial autonomous improvement rate of
CO
2
intensity
0.73%/yr.
Economic damage relative to world GDP
in the case of a 2.5 °C rise
*1
1.8%
(b) Assumed values for evaluating SRM options
Parameter Space Stratosphere
Cost of lifting sun-
shading materials
6000 US$/kg
*2
1 US$/kg
CO
2
emissions via
lifting sunshades
18.5 kgC/kg 0.5 kgC/kg
Mass of sunshades
required to offset
CO
2
doubling
5×10
9
kg 8×10
9
kgS
Depreciation rate of
sunshade stock
5%/yr. 80%/yr.
*1
Rise in global mean air temperature relative to 1900.
*2
Assumed to decline by 2%/yr. from the initial value of 6000
US$/kg in 2005.
2.3 Initial Results: An Outrageous
Influence of SRM on Air
Temperature
Figure 1 shows the trajectory of the global mean air
temperature calculated by using the modified DICE
model described above. The figures hereafter show
the results up to 2125 out of the whole time period
calculated in the model.
As seen from Figure 1, the optimal path of SRM
deployment follows the maximum allowable
implementation starting from 2045 or 2015 if the
space-sunshade installation or the stratospheric
aerosol injection is applicable, respectively. This
result implies that depending largely on an SRM
option can be a more cost-effective measure for
mitigating climatic change than facilitating CO
2
emissions reduction. In this case, as shown in Figure 2
(see “w/o temp. limit” in the figure) the global
industrial CO
2
emission is allowed to rise steadily.
However, in the case of such a large dependency
on SRM for mitigating climate change, we would be
faced with the problem described below should the
implementation of SRM be terminated.
(a) Space sunshade placement
0
0.5
1
1.5
2
2.5
2005 2025 2045 2065 2085 2105 2125
Year
Rise in air temperature (
o
C)
(b) Stratospheric aerosol injection
0
0.5
1
1.5
2
2.5
2005 2025 2045 2065 2085 2105 2125
Year
Rise in air temperature (
o
C)
Figure 1: Global mean air temperature without limiting
temperature rise after SRM termination, °C relative to
1900. The solid line represents the optimal solution while
the broken lines indicate the temperature increases after
termination at the respective time periods.
0
10
20
30
2005 2025 2045 2065 2085 2105 2125
Year
CO
2
emissions (GtC/yr.)
Space, w/o temp. limit
Stratosph., w/o temp. limit
Space, w/ temp. limit
Stratosph., w/ temp. limit
Figure 2: Industrial CO
2
emissions, GtC/yr.
The broken lines in Figure 1 indicate the
temperature increases after SRM termination at the
respective time periods. More specifically, it shows
the calculated global mean air temperature rise
hypothesizing that the values of all the variables, e.g.,
CLIMATE-ECONOMY MODELING CONSIDERING SOLAR RADIATION MANAGEMENT AND ITS
TERMINATION RISK
317

CO
2
emissions, are the same as those calculated
earlier through the model while no new sun-shading
materials are placed into space or the stratosphere
after each of the time periods. The abrupt rise in air
temperature after the SRM termination is called the
“termination problem,” which has been described as
one of the most serious risks concerning the use of
SRM (Brovkin, et al., 2009).
3 EXTENDING THE MODEL TO
MANAGE THE RISK OF SRM
TERMINATION
3.1 Proposal of a Guideline for the Use
of SRM
For the safer use of SRM options, we need to avoid
the risk of abrupt warming, which would occur in a
situation where SRM implementation is terminated.
The causes of termination could include
unsuccessful continuous multilateral political
negotiations regarding SRM or the unexpected
revelation of a major adverse side effect of the SRM.
Although such an occurrence is itself unforeseeable,
the extent of the adverse effect brought about by the
SRM termination can be estimated, and it is possible
to control the use of SRM to keep the damage from
unforeseen discontinuation at a certain allowable
level.
Given the climate control recommendation by
WBGU (2003) to constrain the rise in global average
air temperature below 2 °C and the per-decade rate
of temperature rise within 0.2 °C, a guideline for
SRM use is derived such that the above condition
holds even if SRM is terminated at any time.
3.2 Extension of the Model for Managing
the Risk of the SRM Termination
Problem
The above guideline can be implemented in the
model by introducing the following formulae.
Let
),(
ˆ
ttS
′
be the group of variables
representing the virtual dynamic path of the mass
stock of sun-shading materials accumulated in space
or the stratosphere (Mt) assuming an SRM
termination at time
t
′
. For
tt
′
<
, clearly
)(),(
ˆ
tSttS =
′
,
(5)
while for
Ttt <≤
′
, setting the value of
)(tG
to null
in Eqs. (1) and (1’),
(
)
()
()
⎩
⎨
⎧
−
=
′
+
Stratosph.
Space
0
)',(
ˆ
1
),1(
ˆ
10
ttS
ttS
S
δ
,
(5’)
where
T
denotes the time horizon of the model.
Similarly, when we define variables
),(
ˆ
ttF
′
,
),(
ˆ
ttT
AT
′
, and
),(
ˆ
ttT
LO
′
as the anticipated paths of
total radiative forcing, global mean surface
temperature, and lower ocean temperature in case of
SRM termination at
t
′
, respectively, as in Eq. (2),
[
]
{
)1750()(log),(
ˆ
2 ATAT
MtMttF η =
′
}
)(),(
ˆ
tFmttS
EX
+
′
−
,
(6)
while
),(
ˆ
ttT
AT
′
and
),(
ˆ
ttT
LO
′
are calculated, for
tt
′
<
, as
)(),(
ˆ
tTttT
ATAT
=
′
and
(7)
)(),(
ˆ
tTttT
LOLO
=
′
,
(8)
while for
Ttt
<
≤
′
, consistently with Eqs. (3) and (4),
{
),1(
ˆ
),(
ˆ
),1(
ˆ
1
ttFttTttT
ATAT
′
++
′
=
′
+
ξ
[
]
}
),(
ˆ
),(
ˆ
),(
ˆ
32
ttTttTttT
LOATAT
′
−
′
−
′
−
ξξ
,
(7’)
[
),(
ˆ
),(
ˆ
),1(
ˆ
4
ttTttTttT
ATLOLO
′
+
′
=
′
+
ξ
]
),(
ˆ
ttT
LO
′
−
,
(8’)
where the units of the variables are the same as those
of
)(tF
,
)(tT
AT
, and
)(tT
LO
, respectively.
With respect to
),(
ˆ
ttT
AT
′
defined above, the
following constraints concerning its absolute level
and rate of change are imposed:
2),(
ˆ
≤
′
ttT
AT
,
(9)
2.0),(
ˆ
),1(
ˆ
+
′
≤
′
+ ttTttT
ATAT
.
(10)
These two constraints should be applied for all
t
and
t
′
; however, incorporating Eq. (10) for
3<t
makes
the model infeasible, i.e., the rise in global mean air
temperature in the next decade will inevitably be
above 0.2 °C. We therefore apply Eq. (10) for
3≥t
.
The total numbers of variables and constraints
become 13 and 20 times, respectively, as many as
those of the model before the extension. The
computation time to find the utility maximizing
solution is 41 seconds for the extended model when
space-sunshades are assumed to be available as an
SRM option, which is 27 seconds longer than the pre-
extension when the model is solved by GAMS/
CONOPT3 (Brooke et al., 1992; Drud, 1994) with a
PC based on the Intel(R) Core(TM) 2 Duo CPU
P9300, 2.26GHz with 1.93 GB RAM.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
318

3.3 Results
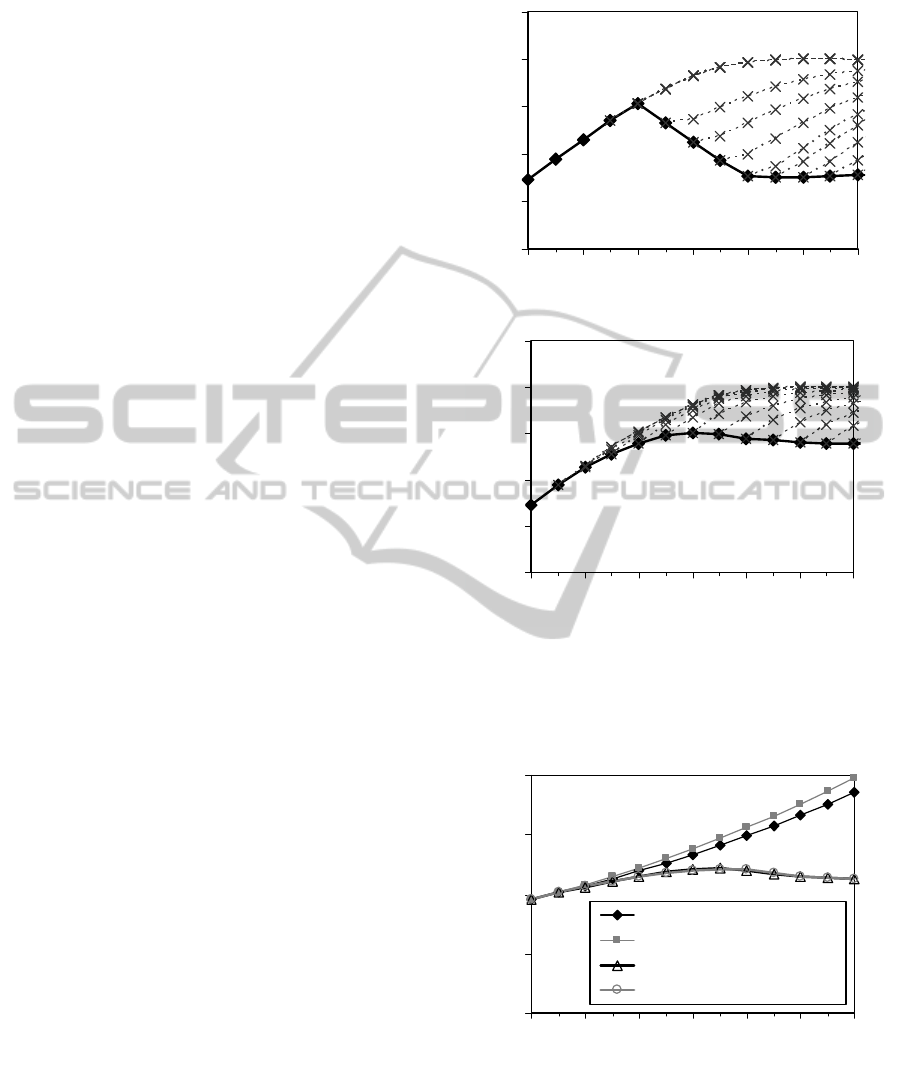
The global mean air temperature calculated through
the extended model is shown as the solid line in
Figure 3. Compared with Figure 1, this figure
suggests a moderate use of SRM, especially in the
case of stratospheric aerosol injection, to lower the
air temperature when we adopt the guideline
introduced above. As in Figure 1, the broken lines in
Figure 3 indicate the trajectory of the temperature
after an unexpected SRM termination at the
respective time periods; we can confirm that, when
the use of SRM is moderated to reflect the guideline
of limiting the temperature rise that would occur by
SRM termination, abrupt warming by SRM use
termination is avoided.
Figure 2 includes the optimal paths of the
industrial CO
2
emissions when the constraint on the
limit of temperature rise in case of SRM termination
is adopted (see “w/ temp. limit”) together with those
without the limit of temperature rise explained in
Section 2.3. The results imply that reducing CO
2
emissions is expected to play a more important role
in mitigating climate change when we adopt the
guideline of limiting temperature rise. Specifically,
the amount of industrial CO
2
emissions should be
kept at around the present level in the former half of
this century and is expected to be reduced rapidly
afterward, reaching only 20% of the 2005 levels by
2085.
Figure 4 shows the calculated atmospheric CO
2
concentration, which steadily increases in this
century and reaches 700 ppmv a century hence if the
guideline of limiting the temperature rise in case of
SRM termination is not adopted. With the limit of
temperature rise in such a case, on the other hand,
the increase in CO
2
concentration is expected to be
mitigated to peak at 490 ppmv by 2075; afterward
the concentration decreases to below 450 ppmv after
2125.
To observe the desirable combination of CO
2
emissions reduction and SRM for contributing to
mitigating climate change derived under the
guideline of limiting temperature rise in case of
SRM termination, the decrease in radiative forcing
by use of each measure to mitigate climate change,
i.e., the difference from the radiative forcing
compared to the case where no climate mitigation
policy is implemented, is illustrated in Figure 5
assuming that stratospheric aerosol injection is
usable as an SRM option.
CO
2
emissions reduction contributes more to
lessening radiative forcing than SRM throughout the
time periods addressed by the model, and the
(a) Space sunshade placement.
0
0.5
1
1.5
2
2.5
2005 2025 2045 2065 2085 2105 2125
Year
Rise in air temperature (
o
C)
(b) Stratospheric aerosol injection.
0
0.5
1
1.5
2
2.5
2005 2025 2045 2065 2085 2105 2125
Year
Rise in air temperature (
o
C)
Figure 3: Global mean air temperature with limiting
temperature rise after SRM termination, °C relative to
1900. The solid line represents the optimal solution while
the broken lines indicate the temperature increases after
termination at the respective time periods.
0
200
400
600
800
2005 2025 2045 2065 2085 2105 2125
Year
CO
2
concentration (ppmv)
Space, w/o temp. limit
Stratosph., w/o temp. limit
Space, w/ temp. limit
Stratosph., w/ temp. limit
Figure 4: Atmospheric CO
2
concentration, ppmv.
contribution of emissions reduction becomes much
greater as time passes. Though we omit a figure
corresponding to the case of using space-based
sunshades instead of stratospheric aerosol injection,
a similar tendency is observed for this case.
CLIMATE-ECONOMY MODELING CONSIDERING SOLAR RADIATION MANAGEMENT AND ITS
TERMINATION RISK
319

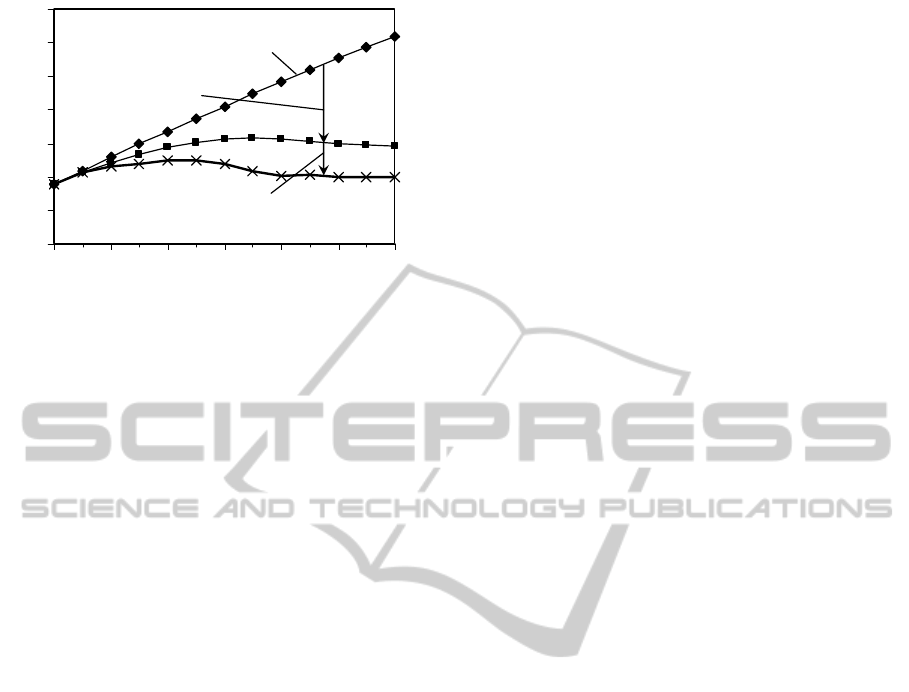
0
1
2
3
4
5
6
7
2005 2025 2045 2065 2085 2105 212
5
Year
Rise in radiative forcing (W/m
2
)
No climate control
CO
2
emissions
reduction
Solar radiation management
Figure 5: Contribution of CO
2
emissions reduction and
SRM to the mitigation of radiative forcing, W/m
2
relative
to 1900, in the case of stratospheric aerosol injection.
4 CONCLUDING REMARKS
SRM geoengineering is expected to be a lower-cost
option of climate control compared to CO
2
emissions reduction, and may considerably
contribute to the cost-effectiveness of global
climatic change mitigation. However, this option is
accompanied by the risk of rapid global warming if
the implementation of SRM is unexpectedly
terminated for any reason. As a guideline for the use
of SRM to avoid the risk, this study suggests that the
adverse effect should be controlled within an
acceptable range in case of unexpected SRM
termination at any time after its implementation. We
incorporated the guideline into the integrated
climate-economy model DICE by extending the
model and quantitatively showed the contributions
of CO
2
emissions reduction and SRM recommended
to prevent global warming.
The extension of the model brings increases in
the numbers of variables and constraint equations,
resulting in a longer computation time to solve the
model. The model is still solved within a minute
using a PC because it incorporates a very simplified
climate module; if we further extend the model to
deal with geographic distribution of climate change,
the computation time is estimated to increase, which
may impose a barrier to practical evaluation.
Finally, it should be emphasized that there are
some risks with the use of SRM other than those
considered in the present modeling study. The
quantitative results obtained from this study should
be interpreted as the economic potential of SRM use
assuming that such risks are low. If we needed to
regard these risks as considerably high, more
restrained use of SRM would be recommended.
REFERENCES
Brooke, A., Kendrick, D., Meeraus, A., 1992. GAMS: A
User's Guide, release 2.25, The Scientific Press, San
Francisco.
Brovkin, V., Petoukhov, V., Claussen, M., Bauer, E.,
Archer, D., Jaeger, C., 2009. Geoengineering climate
by stratospheric sulfur injections. Climatic Change,
92(3-4), 243-259.
Drud, A. S., 1994. CONOPT: A large-scale GRG code.
ORSA Journal on Computing, 6(2), 207-216.
German Advisory Council on Global Change (WBGU),
2003. Climate Protection Strategies for the 21st
Century: Kyoto and Beyond, WBGU, Berlin.
Hertzfeld, H. R., Williamson, R. A., Peter, N., 2005.
Launch Vehicles: An Economic Perspective, George
Washington University Space Policy Institute.
Washington, DC.
Kosugi, T., 2010. Role of sunshades in space as a climate
control option. Acta Astronautica, 67(1-2), 241-253.
Lenton, T., Vaughan, N. E., 2009. The radiative forcing
potential of different climate geoengineering options,
Atmospheric Chemistry and Physics, 9(15), 5539-5561.
McClellan, J., Sisco, J., Suarez, B., Keogh, G., 2010.
Geoengineering Cost Analysis: Final Report, UC01-
001; AR10-182, Aurora Flight Sciences Corporation.
Cambridge, MA.
Nordhaus, W. D., 2008. A Question of Balance: Weighing
the Options on Global Warming Policies, Yale
University Press. New Haven, CT.
Pearson, J., Oldson, J., Levin, E., 2006. Earth rings for
planetary environment control. Acta Astronautica,
58(1), 44-57.
The Royal Society, 2009. Geoengineering the Climate:
Science, Governance and Uncertainty, available via
http://royalsociety.org/geoengineeringclimate/.
Wigley, T. M. L., 2006. A combined mitigation/
geoengineering approach to climate stabilization.
Science, 314, 452–454.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
320