RESEARCH ON WORKFLOW MODELING

BASED ON COLOURED PETRI NET

Zhang Liang, Yao Jiayi

School of Economics and Management, Beijing Jiaotong University, Shang Yuan Cun no.3, Haidian District, Beijing, China

Zhang Yingrui

School of Economics and Management, Beijing Jiaotong University, Shang Yuan Cun no.3, Haidian District, Beijing, China

Keywords: Workflow, Petri Net, Workflow Modeling.

Abstract: Petri as an effective tool for modelling and analyzing processes, which is widely used in the field of

workflow management. This paper introduces the correlation theory of the high-level Petri net with colour

extension and brings forward a workflow modeling method based on coloured Petri net. With the thought, a

workflow model of training institution management is made at last.

1 INTRODUCTION

During the 1990s, workflow management

technology was on the rise, which is widely used in

business management with Business Process

Reengineering (BPR). The crucial point about the

workflow management is workflow modeling,

which is theorization and abstraction of business

process. It is the mirror of description of business

process in computer or system, especially a clear

understanding and awareness. Actually, it is the

basic function of Workflow Management System.

There are several currently proposed methods of

workflow modeling. With the formalized system and

exact definition, Petri net is widely used in the

practical modeling.

2 BASIC CONCEPTIONS

OF WORKFLOW

The principle workflow originated from the field of

production organization and office automation,

which is brought up aiming at constant rule and

operating mechanism in production and work (Sheth,

1993). It is exact and convenient to decompose a

work in operating into many tasks and roles exerting

workflow, while monitoring and constraining every

execution of tasks. So quality and efficiency of

company management should be increased.

Workflow Management Coalition was founded in

1993, which marks that workflow technology will

have a unified standard and enter a relatively mature

step. WFMC suggest a definition of workflow is a

computerised facilitation or automation of a business

process, in whole or part (David Hollingsworth,

2001). It is concerned with the automation of

procedures where documents, information or tasks

are passed between participants according to a

defined set of rules to achieve, or contribute to, an

overall business goal.

3 BASIC CONCEPTION

OF PETRI NET

Petri nets were devised in 1962 by Carl Adam Petri

as a tool for modelling and analyzing processes. One

of the strengths of this tool is the fact that it enables

processes to be described graphically, and we can

use it to present workflow processes in an accessible

way. Despite the fact that Petri nets are graphical,

they have a strong mathematical basis. Unlike many

other schematic techniques, they are entirely

formalized. Because of this formal basis, it is often

possible to make strong statements about the

properties of the process being modelled. There are

423

Liang Z., Jiayi Y. and Yingrui Z..

RESEARCH ON WORKFLOW MODELING BASED ON COLOURED PETRI NET .

DOI: 10.5220/0003593304230426

In Proceedings of the 13th International Conference on Enterprise Information Systems (NMI-2011), pages 423-426

ISBN: 978-989-8425-53-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

also several analysis techniques and tools available

which can be applied to analyze a given Petri net.

Over the years, the model proposed by Carl Adam

Petri has been extended in many different ways, so

that it is possible to model complex processes in an

accessible way.

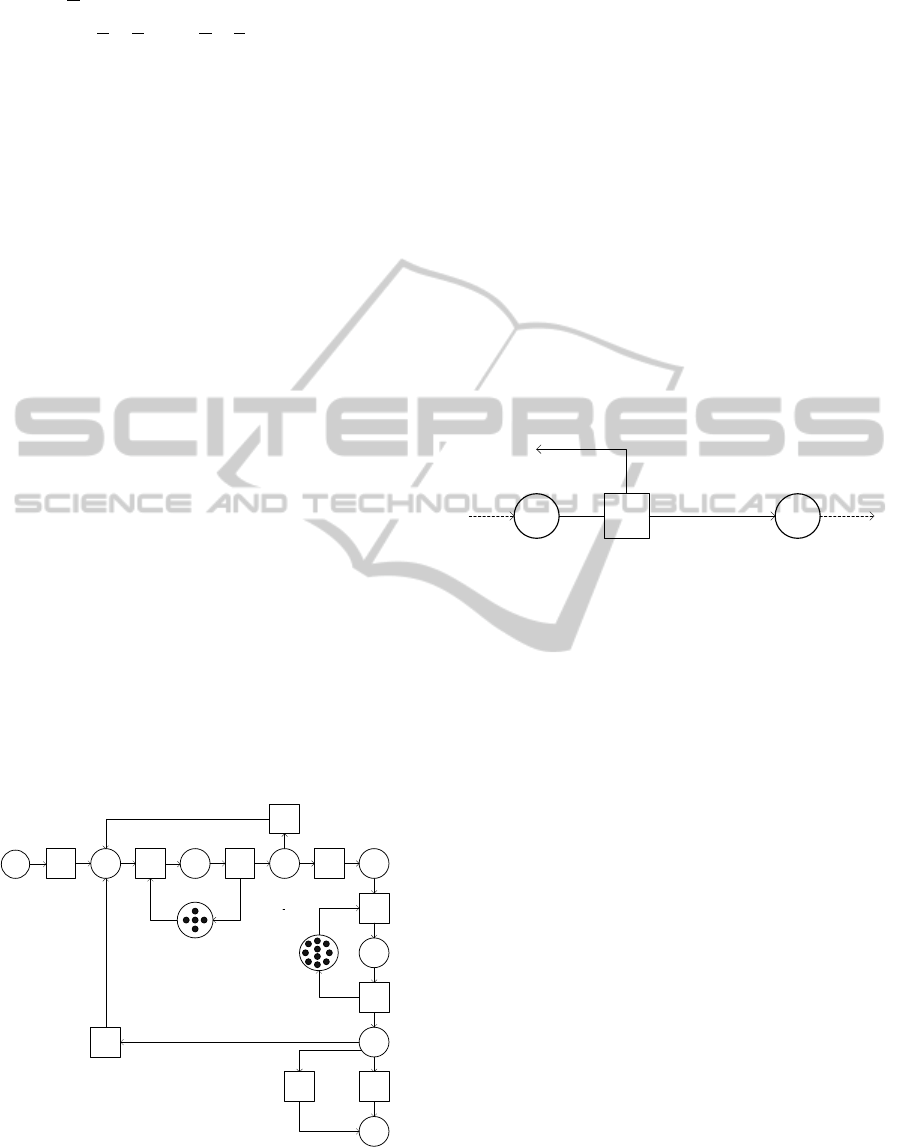
3.1 Classical Petri Net

A Petri net consists of places and transitions. We

indicate a place using a circle. A transition is shown

as a rectangle. Figure1 shows a simple Petri net,

consisting of three places and three transitions.

Figure 1: Classical Petri Net.

Places and transitions in a Petri net can be linked by

means of a directed arc. There are two types of arcs:

those that run from a place to a transition and those

that run from a transition to a place. Arcs from a

place to a place or a transition to a transition are not

possible.

Based upon the arcs, we can determine the input

places of a transition. A place p is an input place for

a transition t if and only if there is a directed arc

running from p to t. Similarly, we can determine the

output places of a transition. A place p is an output

place for a transition t if and only if there is a

directed arc running from t to p. As it happens, in

figure 1 each transition precisely has one input and

one output place.

Places may contain tokens. These are indicated

using black dots. In figure 1 the place claim contains

three tokens. The structure of a Petri net is fixed;

however, the distribution of its tokens among the

places can change. The transition record can thus

take tokens from the claim input place and put them

in under consideration. We call this the firing of the

transition t1. The regulation which the firing of the

transition must obey is that the state of a Petri net is

indicated by the distribution of tokens amongst its

places (Aslas, 1998). A transition may only fire if it

is enabled. This occurs when there is at least one

token at each of its input places. The transitions are

ready to fire. In figure 1, only the transition t1 is

enabled.

As transition fires, one token is removed from each

input place and one token added to each output place.

The change from Figure1 to Figure 2 shows the

effect of t1 firing.

Figure 2: the Petri net after t1 fires.

Therefore, the classical Petri net can be defined

to the mathematical structure as follow.

Definition 1: Quadri-tuple PN = (P, T, F, M

) is

a Petri net only if

(1) P ∩ T = ∅

(2) P ∪ T ≠ ∅

(3) F ⊆ (P×T) ∪ (T×P)

(4) dom(F) ∪ cod(F) = P ∪ T, when

dom(F) = {x | ∃ y:(x , y) ∈ F}

cod(F) = {y | ∃ x:(x, y) ∈ F}

(5) M: P→T, M

is the initial token.

3.2 Coloured Petri Net

Tokens of Petri net are used to model a whole range

of things. In one insurance claim model they can

represent insurance claims, in vehicle production

model can the state of manufacturing. However, in

the classic Petri net it is impossible to distinguish

between two tokens: two in the same place are by

definition indistinguishable. Aiming at this problem,

colour extension is bought to distinguish the tokens

in places (Jensen, 1996).

For example, tokens for students have an age value.

Because of different value, the token can be

distinguished of a certain degree. This method of

valuing tokens is similar to giving different colours.

So we named this extended Petri net as coloured

Petri net.

Coloured Petri net can be defined to the

mathematical structure as follow.

Definition 2: Six-tuple CPN = （P, T, C, I, O,

）is a coloured Petri net only if

(1) P∩T=∅

(2) P∪T≠∅

(3) C = {C(p), C(t)}

(4)

= {<p, c> | p ∈ P, c ∈ C(p)}

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

424

(5)

= {<t, c> | t ∈ T, c ∈ C(t)}

(6) I =

, O =

4 WORKFLOW MODELING

BASED ON COLOURED PETRI

NET

With securities training institution application is

below example undertake demonstrative, which

focus on tracking the progress of the students

training, teacher allocation and student test.

New students register with the training institution. A

registered student takes one or more securities

lessons followed by an examination. Each securities

lesson has a beginning and an end. Instructors give

securities lessons. The driving school has five

securities. Each securities lesson is followed by

either another lesson or an examination. The

examination has a beginning and an end and is

supervised by an examiner. In total there are ten

examiners. For the outcome of an examination there

are three possibilities:

(1) The student passes and leaves the driving school.

(2) The student fails and takes additional lessons in

order to try again.

(3) The student fails and gives up.

Students must takes ten lessons before taking the

exam and people will drop out if they fail three

times.

The workflow model of the securities training

institution is shown in figure 3.

begin

begin_lesson

end_lesson

c2 c3

ready

begin_exam

free_examiners

end_exam

free_teachers

drop_out

pass

end

again

Figure 3: The workflow model of the securities training

institution.

Based on the model in figure 3, we make colour in

the tokens. There is a cc= (token, name, age, gender,

nof_lessons, nof_exams) in place begin, register, c1,

c2, c3, c4, c5, c6 and end, which is mean to a student

who have id, name, age , gender, class-times and

exam-times. For example, there is a new student

named Jack, who is an eighteen boy and has no

lesson and exam.

Nof_lessons and nof_exams are the key points to

this model. The last rule of the training institution is

be clearly described in the model with class-times

and exam-times.

Transitions in the training institution model are

defined as follow.

(1) register：nof_lessons = 0, nof_exams = 0

(2) More and ready are integrated to more1.As the

figure 4 shows, when nof_lessons < 10，make a

token in c1or in c4

c3 more1

nof_lessons=10

nof_lessons<10

Figure 4: More and ready are integrated to more1.

(3) end_lesson：nof_lessons = nof_lessons+1

(4) end_exams：nof_exams = nof_exams+1

(5) again：nof_exams < 3

The result of the color extension is that, in contrast

to the classic Petri net, the graphic representation no

longer contains all the information. For each

transition, the following factors must be specified:

(1) Whether there is a precondition. If there is a

precondition, then this must be defined

precisely.

(2) The number of tokens produced per output

place during each firing. This number may

depend upon the values of the tokens consumed.

(3) The values of the tokens produced. This, too,

may depend upon the values of the tokens

consumed.

Depending upon the objective for which the Petri net

has been produced, the transitions are specified by a

piece of text, a few lines of pseudo-code, a formal

specification, or a subroutine in a programming

language.

RESEARCH ON WORKFLOW MODELING BASED ON COLOURED PETRI NET

425

5 CONCLUSIONS

Classical Petri net is an effective tool to describe

synchronism, asynchronism and distribution in

process, and it can make control and constraint to

resource allocation in workflow. However, it is

complex to model the complex-property workflow

by Classical Petri net, while coloured Petri net can

handle this situation, particularly in distinctions

among roles and organizations. The workflow model

based on coloured Petri net has better ability of

description and analysis. So, there is great

theoretical and realistic significance in research on

workflow modeling based on coloured Petri net.

REFERENCES

David Hollingsworth, 2001. The Workflow Reference

Model. Document Number WFMC – TC – 1003,

Document Status – Issue 1.1.

W. M. P. Vander Aslas, 1998. The Application of Petri

Nets to Workflow Management.WFMC, 2003. The

Journal of Circuis, Systems and Computer.

Yan. Yuhong, Bejan. Alex, 2002. Modeling workflow

within distributed systems. Proceedings of the

International Conference on Computer Supported

Cooperative Work in Design.

Hsu. Chih-Chiang, Huang. Kuo-Chan. 2011. Online

scheduling of workflow applications in grid

environments, Future Generation Computer Systems.

Song. Xudong, Dou. Wanchun, Chen. Jinjun. 2011. A

workflow framework for intelligent service

composition. Future Generation Computer Systems.

A. Sheth, M. Rusinkiewicz, 1993. Transactional

Workflow and Bulletin of the Technical. Committee

on Data Engineering.

Salimifaard k., Mike Wright, 2001. Petri net-based

modeling of workflow system. European Journal of

Operational Research.

Prilr C., 2002. Workflow and process management,

Workflow Management Coalition Handbook.

Tadao Murata, 1989. Petri Net: Properties Analysis and

Applications, Proceedings of the IEEE.

K. Jensen, 1996. Coloured Petri Nets. Springer-Verlag.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

426