
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE
ECOSYSTEM MODEL USING RESPONSE CORRECTION
M. Prieß
1
, S. Koziel
2
and T. Slawig
1
1
Institute for Computer Science, Cluster The Future Ocean, Christian-Albrechts Universit¨at zu Kiel, 24098 Kiel, Germany
2
Engineering Optimization & Modeling Center, School of Science and Engineering, Reykjavik University
Menntavegur 1, 101 Reykjavik, Iceland
Keywords:
Climate models, Marine ecosystem models, Surrogate-based optimization, Parameter optimization, Response
correction.
Abstract:
An improved surrogate-based optimization (SBO) methodology is developed for the optimization of climate
model parameters. Our technique is based upon a multiplicative response correction technique to create a
surrogate from a temporarily coarser discretized physics-based low-fidelity model. The original version of
this methodology was successfully applied to calibration of a (one-dimensional) representative of a class of
marine ecosystem models yielding about 84% computational cost savings when compared to the high-fidelity
model optimization. Here, we demonstrate that by employing relatively simple modifications of the response
correction scheme, the surrogate model accuracy and the efficiency of the optimization process can be further
improved. More specifically, for the considered test case, the optimization cost is reduced three times when
compared to the original technique, i.e., from about 15% to only 5% of the cost of the direct high-fidelity
ecosystem model optimization (used as a benchmark method). The corresponding time savings are increased
to 95%.
1 INTRODUCTION
Surrogate-based optimization (SBO) (Queipo et al.,
2005) is a methodology to efficiently optimize com-
plex, so-called high-fidelity models, that require sub-
stantial computational effort already for a model eval-
uation. High-fidelity models are typically evaluated
through computer simulation and evaluation times of
several hours, days or even weeks are not uncommon.
As a consequence, optimization and control problems
for such models are often still beyond the capability
of modern numerical algorithms and computer power.
The idea of SBO is to exploit a surrogate, a computa-
tionally cheap and yet reasonably accurate representa-
tion of the high-fidelity model. The surrogate replaces
the high-fidelity model in the optimization process in
the sense of providing predictions of the model opti-
mum. Also, it is updated using the high-fidelitymodel
data accumulated during the process. The prediction-
updating scheme is normally iterated in order to refine
the search and to locate the high-fidelity model opti-
mum as precisely as possible. One of possible ways of
creating the surrogate, our work in this paper is based
on, is to utilize a physically-based low-fidelity model.
SBO is widely and very successfully used in engi-
neering sciences (Bandler et al., 2004; Forrester and
Keane, 2009; Leifsson and Koziel, 2010; Queipo
et al., 2005). The application on parameter optimiza-
tion in climate models is new.
Climate models are typically given as time-
dependent partial differential or differential algebraic
equations (PDEs/DAEs) (Majda, 2003; McGuffie and
Henderson-Sellers, 2005; Gill, 1982). One example
are marine ecosystem models (Fennel and Neumann,
2004; Sarmiento and Gruber, 2006), one of which
our work in this paper is based on. Marine ecosys-
tem models describe photosynthesis and other bio-
geochemical processes in the marine ecosystem that
are important, e.g., to compute and predict the oceanic
uptake of carbon dioxide (CO
2
) as part of the global
carbon cycle (Sarmiento and Gruber, 2006). Since the
number of processes that have to be included and the
needed temporal and spatial resolution is quite high,
so is the computational effort.
The aim of parameter optimization is to adjust or
identify the model parameters such that the model re-
sponse fits given measurement data (Banks and Ku-
nisch, 1989). The mathematical task thus can be clas-
sified as a least-squares type optimization or inverse
449
Prieß M., Koziel S. and Slawig T..
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE ECOSYSTEM MODEL USING RESPONSE CORRECTION.
DOI: 10.5220/0003597704490457
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2011), pages
449-457
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
problem (Tarantola, 2005).
This optimization (or calibration) process requires
a substantial number of (typically expensive) function
and optionally sensitivity or gradient or even Hessian
matrix evaluations. Hence, decreasing the effort re-
lated to the function evaluations (or, equivalently, cut-
ting down the number of function calls necessary to
find the optimum) is of primary importance to reduce
the overall optimization cost. This becomes particu-
larly significant for computationally expensive three-
dimensional coupled models, for example, global cli-
mate models (Gill, 1982).
In (Prieß et al., 2011), a surrogate-based method-
ology has been developed for the optimization of
climate model parameters. The technique is based
upon a multiplicative response correction technique
to create a surrogate from a temporarily coarser dis-
cretized physics-based low-fidelity model. It has been
successfully applied to a (one-dimensional) represen-
tative of a class of marine ecosystem models and
demonstrated to yield substantial savings of the com-
putational cost of the optimization process when com-
pared to a direct optimization of the high-fidelity
model.
In this paper, we demonstrate that by employing
simple modifications of the original response correc-
tion scheme, one can improve the surrogate’s accu-
racy, as well as further reduce the computational cost
of the optimization process. We verify our approach
by using synthetic target data and by comparing the
results of SBO with the improved surrogate to those
obtained with the original one. The optimization cost
is reduced three times when compared to previous re-
sults, i.e., from about 15% to only 5% of the cost of
the direct high-fidelity ecosystem model optimization
(used as a benchmark method). The corresponding
time savings are increased to from 84% to 95%.
The paper is organized as follows. The high-
fidelity ecosystem model, considered here as a test
problem, as well as a low-fidelity counterpart that we
use as a basis to construct the surrogate model, are de-
scribed in Section 2. The optimization problem under
consideration is formulated in Section 3. The orig-
inal and improved response correction schemes and
the comparison of the corresponding surrogate model
qualities are discussed in Section 4. Numerical results
for an illustrative SBO run are provided in Section 5.
Section 6 concludes the paper.
2 MODEL DESCRIPTION
The considered example for a climate model is a one-
dimensional marine ecosystem model (Oschlies and
Garcon, 1999) driven by pre-computed ocean circula-
tion data. In the following, we briefly describe the
high-fidelity model and its low-fidelity counterpart
which is a basis to construct a surrogate for further
use in the optimization process.
2.1 The High-fidelity Model
Simulating the marine ecosystem has become a key
tool for understanding the ocean carbon cycle and its
variability. The marine ecosystem contains several
biogeochemical quantities (called tracers), for exam-
ple nutrients, phyto- and zooplankton which inter-
act and are moreover transported by the ocean cir-
culation and influenced by temperature and salinity.
Thus, ecosystem simulations require modeling and
computation of both ocean circulation and biogeo-
chemistry. The underlying continuous models are
governed by coupled systems of nonlinear, parabolic
PDEs or DAEs, for ocean circulation (ocean models,
i.e., Navier-Stokes equations with additional temper-
ature and salinity transport equations) and transport
of biogeochemical tracers (marine ecosystem models,
i.e., convection- or advection-diffusion-reaction type
equations) (Sarmiento and Gruber, 2006).
In ecosystem models, the parameters to be opti-
mized – in the following summarized in the vector u
– are, for example, growth and dying rates of the trac-
ers and thus appear in the usually nonlinear coupling
or interaction terms in the model.
0 2000 4000 6000 8000 10000
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time [ hours ]
Detritus [ mmol N m
−3
]
y
d
y(u)
Figure 1: Model response y
(D)
(detritus) and observation
data y
(D)
d
for one year at depth z ≃ −25m.
Our example ecosystem model was developed by
Oschlies and Garcon (1999)and simulates the interac-
tion of dissolved inorganic nitrogen, phytoplankton,
zooplankton and detritus (dead material) – thus also
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
450

called NPZD model. One aim was to reproduce ob-
servations y
d
at different North Atlantic locations by
the optimization of model parameters within credible
limits. Figure 1 shows the model response and target
data, respectively, as illustration for the tracer detritus
for a certain depth and a part of the time interval.
The model uses pre-computed ocean circulation
and temperature data from an ocean model (in a some-
times called off-line modus), i.e., no feedback by the
biogeochemistry on the circulation and temperature is
modeled (Oschlies and Garcon, 1999).
Since biogeochemistry happens locally and sink-
ing processes only in the vertical water column, we
use here a one-dimensional version of the model at
a given horizontal position. This is additionally mo-
tivated by the fact that there have been special time
series studies at fixed locations. Clearly, the compu-
tational effort of a one-dimensional simulation is sig-
nificantly smaller than for the three-dimensional case.
Thus, since the one-dimensional case includes all sig-
nificant features of ecosystem models, it can serve as
a good verification example for testing the applica-
bility of surrogate-based approaches that can be later
exploited for optimizing the 3D model.
In the NPZD model, the concentrations (in
mmol N m
−3
) of dissolved inorganic nitrogen N, phy-
toplankton P, zooplankton Z, and detritus D are sum-
marized in the vector y = (y
(l)
)
l=N,P,Z,D
and described
by the following coupled PDE system
∂y
(l)
∂t
=
∂
∂z
κ
∂y
(l)
∂z
!
+
Q
(l)
(y,u
2
,... , u
n
), l = N,P,Z
∂y
(D)
∂t
=
∂
∂z
κ
∂y
(D)
∂z
!
+
Q
(D)
(y,u
2
,... , u
n
) −
∂y
(D)
∂z
u
1
, l = D
(1)
in (−H,0) × (0, T) with additional appropriate initial
values. Here, z denotes the only remaining, verti-
cal spatial coordinate, and H the depth of the water
column. The terms Q
(l)
are the biogeochemical cou-
pling (or source-minus-sink) terms for the four tracers
and u = (u
1
,... , u
n
) is the vector of unknown physi-
cal and biological parameters. The sinking term is
only apparent in the equation for detritus. In the
one-dimensional model no advection term is used,
since a reduction to vertical advection would make no
sense. Thus, the circulation data (taken from an ocean
model) are the turbulent mixing coefficient κ = κ(z,t)
and the temperature Θ = Θ(z,t), which goes into the
nonlinear coupling terms Q
(l)
but is omitted in the no-
tation.
The continuous model (1) is discretized and
solved using an operator splitting method (Marchuk,
1982), an explicit euler timestepping scheme for the
nonlinear coupling term Q and the sinking term while
using an implicit euler timestepping scheme for the
diffusion term. For further details we refer the reader
to (Prieß et al., 2011).
In the original model, the time step denoted by τ,
is chosen as one hour. The model with this particular
time step will be referred to as the high-fidelity or fine
one.
In the following, we will denote by y
j
≈ y(·,t
j
) the
discrete fine model solution of the continous model
(1) in time step j (containing all tracers N,P,Z,D)
given as
y
j
= (y
ji
)
i=1,...,I
, j = 1,.. . , M, y ∈ R
MI
(2)
where I = 66 × 4 denotes the number of spatial dis-
crete points for all tracers given by 66, the number of
spatial discrete points per tracer, times 4, the num-
ber of tracers (cf. (1)) and where M = 8760 time
steps/year × 5 years denotes the number of discrete
time steps for each tracer.
2.2 Low-fidelity Model
The low-fidelity (or coarse) model, which is a less ac-
curate but computationally cheap representation of y
is obtained by using a coarser time discretization
ˆ
τ
given as
ˆ
τ = βτ (3)
with a coarsening factor β ∈ N \{ 0,1}, while keeping
the spatial discretization fixed. The state variable for
this coarser discretized model will be denoted by
ˆ
y,
the corresponding number of discrete time steps by
ˆ
M = M/β, i.e., we have
ˆ
y
j
= ( ˆy
ji
)
i=1,...,I
, j = 1,... ,
ˆ
M,
ˆ
y ∈ R
ˆ
MI
. (4)
Note that the parameters u for this coarse model are
the same as for the fine model.
The low-fidelity model is used to create the sur-
rogate of the high-fidelity model, subsequently ex-
ploited to optimize the latter at a low computational
cost (cf. Section 4).
3 OPTIMIZATION PROBLEM
The key task in parameter optimization is to mini-
mize a least-squares type cost function measuring the
misfit between the discrete model output y = y(u)
and given observational data y
d
(Banks and Kunisch,
1989; Tarantola, 2005). In most cases, the problem is
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE ECOSYSTEM MODEL USING RESPONSE
CORRECTION
451

constrained by parameter bounds. Thus the parameter
optimization problem can be written as
min
u∈U
ad
J( y(u)) (5)
where
J( y) :=
1
2
||y− y
d
||
2
,
U
ad
:= {u ∈ R
n
: b
l
≤ u ≤ b
u
},
b
l
,b
u
∈ R
n
, b
l
< b
u
.
The inequalities in the definition of the set U
ad
of ad-
missible parameters are meant component-wise. The
functional J may additionally include a regularization
term for the parameters, which was not necessary in
our case.
Additional constraints on the state variable y
might be necessary, e.g., to ensure non-negativity of
the temperature or of the concentrations of biogeo-
chemical quantities. In our example model however,
by using appropriate parameter bounds b
l
and b
u
,
non-negativity of the state variables can be ensured.
This was already observed and used in (R¨uckelt et al.,
2010).
4 SURROGATE-BASED
OPTIMIZATION
For many nonlinear optimization problems, a high
computational cost of evaluating the objective func-
tion and its sensitivity, and, in some cases, the lack
of sensitivity information, is a major bottleneck. The
need for decreasing the computational cost of the op-
timization process is especially important while han-
dling complex three-dimensional models.
Surrogate-based optimization (Bandler et al.,
2004; Forrester and Keane, 2009; Leifsson and
Koziel, 2010; Queipo et al., 2005) is a methodology
that addresses these issues by replacing the original
high-fidelity model y by a surrogate, in the following
denoted by s, a computationally cheap and yet reason-
ably accurate representation of y.
Surrogates can be created by approximating sam-
pled high-fidelity model data (functional surrogates).
Popular techniques include polynomial regression,
kriging, artificial neural networks and support vector
regression (Queipo et al., 2005; Smola and Sch¨olkopf,
2004; Simpson et al., 2001). Another possibility,
exploited in this work, is to construct the surro-
gate model through appropriate correction/alignment
of a low-fidelity or coarse model (physically-based
surrogates) (Søndergaard, 2003). The advantage of
physically-based surrogates is that a reasonable accu-
racy can be obtained using a limited number of high-
fidelity model data. Also, generalization capability of
the physically-based models is typically much better
than for functional ones. The specific correction tech-
nique exploited in this work is described below.
The surrogate model is updated at each iteration
k of the optimization algorithm, typically using avail-
able high-fidelity model data. The next iterate, u
k+1
,
is obtained by optimizing the surrogate s
k
, i.e.,
u
k+1
= argmin
u∈U
ad
J( s
k
(u)). (6)
Then, the updated surrogate s
k+1
is determined by
re-aligning the low-fidelity model at u
k+1
and opti-
mized again as in (6). The process of aligning the
coarse model to obtain the surrogate and subsequent
optimization of this surrogate is repeated until a user-
defined termination condition is satisfied.
If the surrogate s
k
satisfies so-called zero-order
and first-order consistency conditions (Conn et al.,
2000; Koziel et al., 2010) with the high-fidelity
model at u
k
, i.e., s
k
(u
k
) = y(u
k
), s
′
k
(u
k
) = y
′
(u
k
) the
surrogate-based scheme (6) is provably convergent to
at least a local optimum of (5), provided that both the
low- and high-fidelity models are sufficiently smooth,
and the surrogate optimization step is enhanced by the
the trust-region (TR) safeguard (Conn et al., 2000;
Koziel et al., 2010). The surrogate model utilized
in this work only satisfies the zero-order consistency
with the high-fidelity model. Still, as demonstrated in
Section 5, the performance of our surrogate-based op-
timization process is satisfactory even without using
the trust-region convergence safeguards.
4.1 Surrogate Model using Basic
Multiplicative Response Correction
The multiplicative response correction is one reason-
able way to construct a physically-based surrogate for
the marine ecosystem model given in Section 2.1.
This approach was successfully exploited in (Prieß
et al., 2011), and it is briefly recalled below.
The surrogate response s
k
(u), at iteration k of
the optimization process, is generated by multiplica-
tive correction of the smoothed low-fidelity model re-
sponse (cf. Subsection 2.2), denoted by
˜
ˆ
y, yielding
s
kji
(u) := A
kji
˜
ˆy
ji
(u),
A
kji
:=
˜y
β
ji
(u
k
)
˜
ˆy
ji
(u
k
)
k = 1,2,.. .
j = 1,.. . ,
ˆ
M
i = 1,. . . ,I
β = M/
ˆ
M
(7)
where A
kji
denotes the correction factor given as
the point wise division of the smoothed and down-
sampled fine model response, denoted by
˜
y
β
, by the
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
452

500 1000 1500 2000 2500 3000 3500 4000
0
0.1
0.2
0.3
time [ hours ]
DET [mmol N m
−3
]
˜y
β
(u
k
)
˜
ˆy(u
k
)
s
k
(u
k
)
˜y
β
(
¯
u
k
)
˜
ˆy(
¯
u
k
)
s
k
(
¯
u
k
)
0 500 1000 1500 2000 2500 3000 3500
0.1
0.2
0.3
00
time [ hours ]
DET [mmol N m
−3
]
Figure 2: Surrogate’s, fine (down-sampled, smoothed) and coarse (smoothed) model responses s
k
,
˜
y
β
and
˜
ˆ
y for the tracer
detritus (at depth z ≈ −2.68m) at two points u
k
and corresponding perturbations
¯
u
k
(see the text for details). The surrogate,
established at u
k
, is perfectly aligned with the fine model at u
k
and provides a reasonable approximation of the fine model
response at
¯
u
k
. For illustration, only the model responses for one representative tracers, depth layer, and a part of the whole
time interval is shown.
smoothed coarse model response at the point u
k
. This
simple correction scheme is justified by the fact that
the overall ”shape” of the low-fidelity model response
resembles that of the high-fidelity one.
It was observed that smoothing allows us to re-
move the numerical noise from the coarse model re-
sponse and identify the main characteristics of the
traces of interest. Consequently, also the (down-
sampled) fine model response is smoothed in (7),
yielding
˜
y
β
, before calculating the multiplicative cor-
rection factor. Sampling of the fine model response
was necessary to make it commensurable with the
corresponding coarse model response. The sampled
fine model response y
β
is given as
y
β
ji
:= y
βj,i
, j = 1,...,
ˆ
M, i = 1,.. . , I,
y
β
∈ R
ˆ
MI
. (8)
The correction step in iteration k on the whole discrete
state vector is given as
s
k
(u) := A
k
◦
˜
ˆ
y(u), s
k
∈ R
ˆ
M
I
,
A
k
:=
A
kji
j,i
∈ R
ˆ
M×I
(9)
where A
k
, the correction matrix in step k, and the op-
eration “◦” are defined by (7).
By definition the surrogate model is zero-order
consistent with the (down-sampled and smoothed)
fine model in the point u
k
(i.e. s
k
(u
k
) ≈
˜
y
β
(u
k
)).
As we do not use sensitivity information, the first-
order consistency condition cannot be satisfied ex-
actly. Nevertheless, as was shown in (Prieß et al.,
2011), this surrogate model exhibits quite good gen-
eralization capability, which means that the surro-
gate provides a reasonable approximation of the high-
fidelity one in the neighborhood of u
k
.
Figure 2 shows the surrogate’s, fine (down-
sampled) and coarse model responses
˜
y
β
,
˜
ˆ
y,s
k
at two
different points, u
k
and
¯
u
k
. The surrogate model is
established at u
k
and, therefore, its output is perfectly
aligned with the fine model output at u
k
. The surro-
gate model prediction is still good at
¯
u
k
. Since the dis-
tance between subsequent iterations points normally
decrease upon convergence of the optimization algo-
rithm, the prediction of the surrogate model is becom-
ing more and more accurate towards the end of the
optimization run.
4.2 Difficulties of Basic Surrogate
Formulation
Occasionally, when using the surrogate given in (7),
there might occur a situation where the coarse model
response is close to zero (and maybe even negative
due to approximation errors) and a few magnitudes
smaller than the fine one, which leads to large (possi-
bly negative) entries in the corresponding correction
tensor A
k
. While such a correction tensor ensures
zero-order consistency at the point where it was es-
tablished (i.e., u
k
), it may lead to (locally) poor ap-
proximation in the vicinity of u
k
.
Figure 3 (left) illustrates these issues by showing
the smoothed surrogate’s, fine (down-sampled) and
coarse model responses
˜
y
β
,
˜
ˆ
y,s
k
for the state detri-
tus at one illustrative time interval and depth layer.
Shown are the model responses at the same iterations
u
k
and its neighborhood
¯
u
k
∈ B
δ
(u
k
) as in Figure 2.
It should be pointed out that the overall shape
of the surrogate’s response provides a reasonable ap-
proximation of the fine model response (and more ac-
curate than the corresponding coarse model response)
despite of the distortion illustrated in Figure 3. This
is supported by the fact that even without addressing
these issues, the surrogate-based scheme (6) was able
to yield satisfactory results, not only with respect to
the quality of the final solution, but, most importantly,
in terms of the low computational cost of the opti-
mization process. This was demonstrated in (Prieß
et al., 2011).
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE ECOSYSTEM MODEL USING RESPONSE
CORRECTION
453

3.7 3.8 3.9 4 4.1 4.2
x 10
4
0
0.1
0.2
time [ hours ]
DET [mmol N m
−3
]
˜y
β
(u
k
)
˜
ˆy(u
k
)
s
k
(u
k
)
˜y
β
(
¯
u
k
)
˜
ˆy(
¯
u
k
)
s
k
(
¯
u
k
)
3.7 3.8 3.9 4 4.1 4.2
x 10
4
0
0.1
0.2
time [ hours ]
DET [mmol N m
−3
]
Figure 3: Surrogate’s, fine (down-sampled, smoothed) and coarse (smoothed) model responses s
k
,
˜
y
β
and
˜
ˆ
y for the same
representative tracer, depth layer and parameter vectors u
k
and
¯
u
k
as in Figure 2 while showing a different time interval.
Using the basic surrogate formulation (9), possible large positive and negative entries in the corresponding correction tensor
A
k
may lead to (locally) poor approximation of the resulting surrogate in the vicinity of u
k
(left). However, the overall shape
of the surrogate still provides a reasonable approximation of the fine one (and more accurate than the corresponding coarse
model response). Employing the improvements in (10) the large positive and negative peaks are removed (right). See the text
for details.
4.3 Improved Response Correction
Scheme
The response distortion described in the previous sec-
tion is problematic towards the end of the surrogate-
based optimization run when the small changes of the
model parameters and the corresponding responses
are considered. The ”‘spikes”’ appearing in the re-
sponse due to large values of the correction term can
be viewed, in a way, as a numerical noise that slows
down the algorithm convergence and makes the opti-
mum more difficult to locate.
A few simple means described below can address
these issues and further improve the accuracy of the
surrogate’s response as well as the performance of the
optimization algorithm.
We introduce non-negative bounds for the coarse
model response (the negative response is non-
physical and is a result of numerical errors due to
using large time steps in the coarse model), upper
bounds for the correction factor as well as restrict the
correction factor to one in case the fine and coarse
model responses are below a certain threshold ε.
Here, we use ε = 10
−10
. More specifically, the fol-
lowing modifications of the model outputs and the
scaling factors are performed for each iteration k, dis-
crete time step j and depth layer i:
(i) ˆy
ji
(u
k
) = max{ ˆy
ji
(u
k
),1e− 8 }
(ii) A
kji
= min{ A
kji
,10 }
(iii) A
kji
= 1 if
˜y
β
ji
(u
k
) ≤ ε and
˜
ˆy
ji
(u
k
) ≤ ε
(10)
where (i) is employed before smoothing the coarse
model response.
Figure 3 (right) shows the surrogate’s, fine (down-
sampled) and coarse model response for the same il-
lustrative tracer, time interval and depth layer as Fig-
ure 3 (left), however, while employing the improve-
ments given in (10). It can be observed that the large
positive and negative peaks present in the surrogate
responses of Figure 3 (left) are removed after apply-
ing (10).
The numerical results presented in Section 5
demonstrate that this improved response correction
scheme allows us to further improve the computa-
tional efficiency of the surrogate-based scheme (6).
5 NUMERICAL RESULTS
The optimization setup used in this work is the follow-
ing. For all optimization runs we use the MATLAB
1
function
fmincon
, exploiting the active-set algorithm.
The following cost functions
J( z) := || z− y
d
||
2
=
I
∑
i=1
ˆ
M
∑
j=1
(z
ji
− (y
d
)
ji
)
2
, (11)
˜
J( z) := || z−
˜
y
d
||
2
=
I
∑
i=1
ˆ
M
∑
j=1
(z
ji
− ( ˜y
d
)
ji
)
2
, (12)
(y
d
)
ji
:= y
β
ji
(u
d
), z ∈ R
ˆ
MI
were used for the fine model optimization ((11) with
z = y
β
), for the coarse model ((12) with z =
˜
ˆ
y) and
surrogate optimization ((12) with z = s
k
), whereas
(11) was used in the termination condition and to
compare the results. The down-sampled fine model
output is given by (8) and the target data y
d
– as a first
illustration – was synthetically created by the (down-
sampled) fine model output at parameter vector u
d
.
Sampling was necessary to yield a comparable fine
1
MATLAB is a registered trademark of The MathWorks,
Inc., http://www.mathworks.com
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
454
0 50 100 150 200 250 300 350 400
0
1
2
3
4
5
6
x 10
4
# of equivalent fine model evaluations
J ( y
β
(u) )
fine model opt.
coarse model opt.
SBO, original correction scheme
SBO, improved correction scheme
0 10 20 30 40 50 60
0
5000
10000
15000
≈96 %
≈84 %
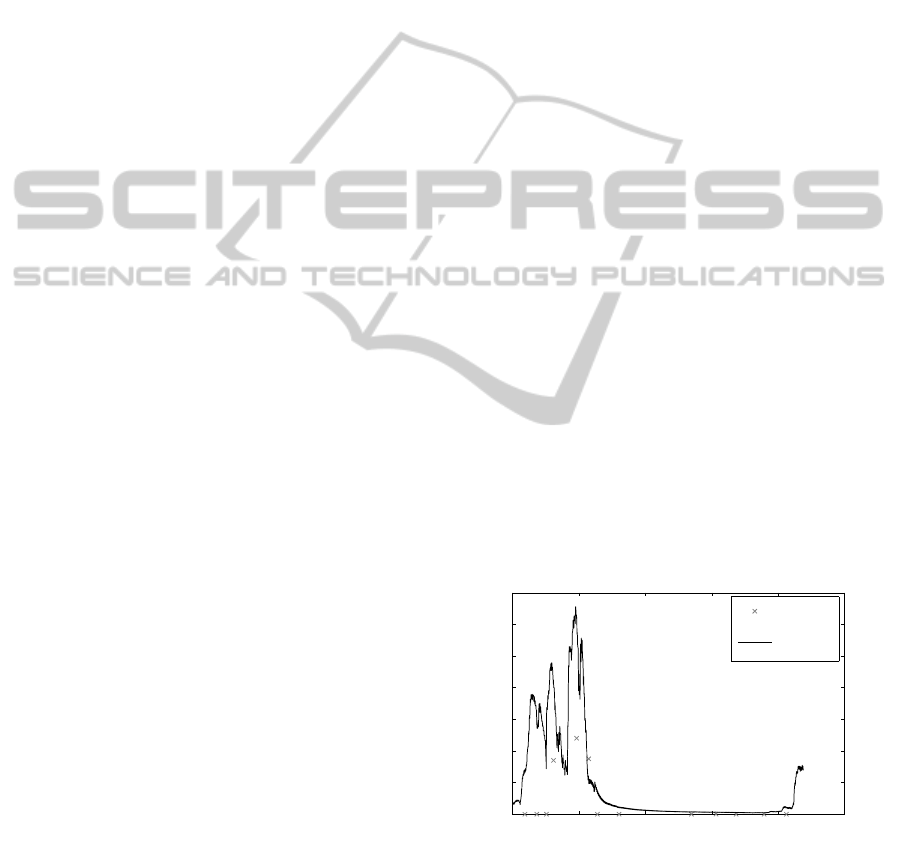
Figure 4: Values of the cost function J (cf. (11)) versus the equivalent number of fine model evaluations for a SBO run
using the surrogate model exploiting the original (cf. (7)) and the improved correction scheme (cf. (10)), as well as for a fine
and coarse model optimization run. The figure also indicates those points in the SBO runs that correspond to a termination
condition of J( y
β
(u
k
)) ≤ 50, ensuring good visual agreement between the fine model output and the target. After employing
the improvements suggested in (10), the number of equivalent fine model evaluations required to satisfy this termination
condition was reduced from 60 down to only 17, resulting in an increase of the corresponding time savings, from 84% to
about 96%, when compared to the direct fine model optimization.
model optimization run while in (12) smoothing of
the target data is performed since smoothing of the
coarse model and surrogate’s response was employed
in the corresponding optimization runs.
For the sake of comparison, we run the direct
fine and coarse model optimizations as well as the
surrogate-based algorithm (cf. (6)) exploiting the
original and improved response correction scheme (7)
and (10).
Results are presented in Figure 4 showing the
value of the cost function J (cf. (11)) versus the equiv-
alent number of fine model evaluations for the SBO
algorithm using the surrogate model exploiting the
original and the improved correction scheme, as well
as for the fine and coarse model optimization (Prieß
et al., 2011). Equivalent fine model evaluations are
determined taking into account the coarsening fac-
tor β. More specifically, one evaluation of the coarse
model with a coarsening factor β is equivalent to 1/β
evaluations of the fine model. The total optimization
cost is calculated as n
f
+ n
c
/β, where n
f
(n
c
) denotes
the overall number of fine (coarse) model evaluations
during the optimization run. Recall that SBO scheme
6 requires one fine model evaluation per algorithm it-
eration.
Figure 4 indicates the points in the SBO run that
correspond to a termination condition of J( y
β
(u
k
)) ≤
50. This particular value was selected as it ensures
good visual agreement between the fine model output
and the target.
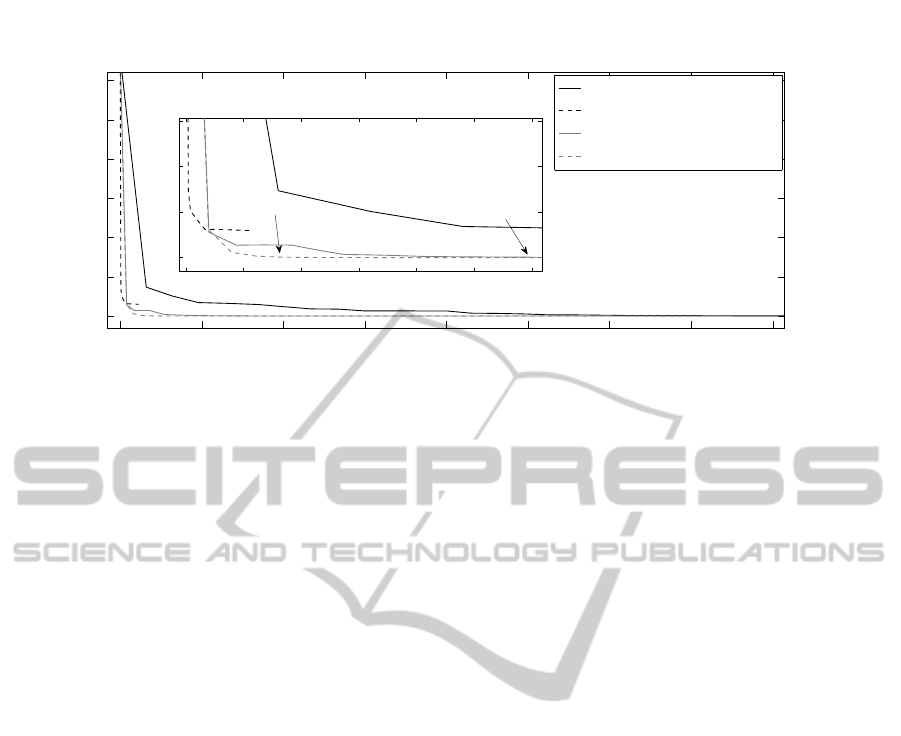
Figure 5 shows the down-sampled fine model re-
sponse for the optimal parameter values obtained us-
ing the SBO algorithm with the original and improved
response correction scheme (denoted by u
∗
s,1
,u
∗
s,2
).
Only two tracers at a certain depth level and time in-
terval are included for illustration. For the sake of
completeness the responses obtained through the di-
rect fine and coarse model optimization, denoted by
u
∗
,
ˆ
u
∗
, are also included.
It should be noted that the model parameters ob-
tained by directly optimizing the coarse model result
in a cost function value of J(y
β
(
ˆ
u
∗
)) ≈ 2960 (opti-
mization cost: 11 equivalent fine model evaluations)
(cf. Figure 4). This solution is far away from that ob-
tained by the direct fine model optimization (cf. Fig-
ure 5), which indicates that the coarse model is not a
reliable prediction tool.
Direct fine model optimization yields a very low
cost function of J(y
β
(
ˆ
u
∗
)) ≈ 1.267 · 10
−2
, corre-
sponding to a solution close to the target data (cf. Fig-
ure 5). However,the optimization cost is substantially
higher: 983 fine model evaluations. Note that for bet-
ter readability, Figure 4 only shows the range 0-400
function evaluations.
In (Prieß et al., 2011), we demonstrated that in
the SBO run based on the original response correc-
tion scheme (7), the chosen termination condition
J( y
β
(u
k
)) ≤ 50 could be reached after approximately
60 equivalent fine model evaluations. This resulted
in a reduction of the total optimization cost of about
84% when compared to the fine model optimization
(the direct fine model optimization required 375 eval-
uations to reach this cost function value, cf. Figure 4).
After employing the improvements suggested in
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE ECOSYSTEM MODEL USING RESPONSE
CORRECTION
455

500 1000 1500 2000 2500 3000
0
0.5
1
1.5
time [ days ]
DIN [mmol N m
−3
]
y
β
(u
d
)
y
β
(u
0
)
y
β
(u
∗
)
y
β
(
ˆ
u
∗
)
y
β
(u
∗
s1
)
y
β
(u
∗
s2
)
500 1000 1500 2000 2500 3000
0
0.1
0.2
0.3
0.4
0.5
time [ hours ]
DET [mmol N m
−3
]
Figure 5: Fine model output y
β
(down-sampled) for state dissolved inorganic nitrogen (left) and the state detritus (right) at
depth z ≈ −2.68m. Shown are, in the legend from top to bottom: (i) Target y
d
, (ii) fine model output at the initial value u
0
, (iii)
at the result of the direct fine model optimization yielding u
∗
, (iv) at the coarse model optimum
ˆ
u
∗
and (iv), (v) at the optima
u
∗
s1
,u
∗
s2
obtained by the surrogate-based algorithm (6) exploting the original (cf. (7)) and the improved (cf. (10)) response
correction scheme. Solutions (iv) and (v) are both very close to (iii) but the solution (v) was obtained at the computational
cost three times lower than (iv).
(10), only 17 equivalent fine model evaluations were
required to satisfy the same termination condition,
which is over three times less than for the original
response correction scheme. The corresponding re-
duction of the total optimization cost, compared to the
direct fine model optimization, is about 96% (cf. Fig-
ure 4). The corresponding solution is close to that
obtained by direct fine model optimization as shown
in Figure 5.
6 CONCLUSIONS
Parameter optimization in climate models can be very
expensive in terms of the cost function and gradient
evaluations, especially for three-dimensional cases.
Therefore, methods that aim at reducing the optimiza-
tion cost of such high-fidelity (fine) models, such as
surrogate-based optimization (SBO) techniques, are
highly desirable. Here, the idea is to replace the fine
model in the optimization run by a surrogate, a com-
putationally cheap and yet reasonably accurate repre-
sentation.
As a case study, we are interested in a parameter
optimization of a one-dimensional representative of a
class of marine ecosystem models. It follows that a
simple multiplicative response correction applied to
a temporarily coarser discretized physics-based low-
fidelity (coarse) model of the system of interest is
sufficient to create a reliable surrogate of the orig-
inal, high-fidelity ecosystem model. This approach
allowed us to yield remarkably good results, both in
terms of the quality of the final solution and, most im-
portantly, in terms of the relative reduction in the total
optimization cost, about 84% when compared to the
direct fine model optimization.
In this paper, we demonstrated that the correction
scheme can be enhanced to alleviate the difficulties of
its original version, which results in further improve-
ment of the surrogate model accuracy and overall per-
formance of the optimization algorithm utilizing this
surrogate. The optimization cost was reduced by a
factor of three (from 16% to 5% of the direct high-
fidelity model optimization optimization cost), which
corresponds to the cost savings of 95%.
ACKNOWLEDGEMENTS
The authors would like to thank Andreas Oschlies,
IFM Geomar, Kiel.
REFERENCES
Bandler, J. W., Cheng, Q. S., Dakroury, S. A., Mohamed,
A. S., Bakr, M. H., Madsen, K., and Søndergaard, J.
(2004). Space mapping: The state of the art. IEEE T.
Microw. Theory., 52(1).
Banks, H. T. and Kunisch, K. (1989). Estimation Tech-
niques for Distributed Parameter Systems. Birkh¨auser.
Conn, A. R., Gould, N. I. M., and Toint, P. L. (2000). Trust-
region methods. Society for Industrial and Applied
Mathematics, Philadelphia, PA.
Fennel, W. and Neumann, T. (2004). Introduction to the
Modelling of Marine Ecosystems. Elsevier.
Forrester, A. I. and Keane, A. J. (2009). Recent advances
in surrogate-based optimization. Prog. Aerosp. Sci.,
45(1-3):50–79.
Gill, A. E. (1982). Atmosphere - Ocean Dynamics, vol-
ume 30 of International Geophysics Series. Academic
Press.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
456

Koziel, S., Bandler, J. W., and Cheng, Q. S. (2010). Ro-
bust trust-region space-mapping algorithms for mi-
crowave design optimization. IEEE T. Microw. The-
ory., 58(8):2166–2174.
Leifsson, L. and Koziel, S. (2010). Multi-fidelity de-
sign optimization of transonic airfoils using physics-
based surrogate modeling and shape-preserving re-
sponse prediction. Journal of Computational Science,
1(2):98–106.
Majda, A. (2003). Introduction to PDE’s and Waves for the
Atmosphere and Ocean. AMS.
Marchuk, G. I. (1982). Methods of Numerical Mathematics.
Springer, 2nd edition.
McGuffie, K. and Henderson-Sellers, A. (2005). A Climate
Modelling Primer. Wiley, 3nd edition.
Oschlies, A. and Garcon, V. (1999). An eddy-permitting
coupled physical-biological model of the north at-
lantic. 1. sensitivity to advection numerics and mixed
layer physics. Global Biogeochem. Cy., 13:135–160.
Prieß, M., Koziel, S., and Slawig, T. (2011). Surrogate-
based optimization of climate model parameters us-
ing response correction. Preprint 1104, Christian-
Albrechts-Universit¨at zu Kiel, Institute for Computer
Science.
Queipo, N. V., Haftka, R. T., Shyy, W., Goel,
T., Vaidyanathan, R., and Tucker, P. K. (2005).
Surrogate-based analysis and optimization. Prog.
Aerosp. Sci., 41(1):1–28.
R¨uckelt, J., Sauerland, V., Slawig, T., Srivastav, A., Ward,
B., and Patvardhan, C. (2010). Parameter optimiza-
tion and uncertainty analysis in a model of oceanic
co2-uptake using a hybrid algorithm and algorithmic
differentiation. Nonlinear Analysis: Real World Ap-
plications, online.
Sarmiento, J. and Gruber, N. (2006). Ocean Biogeochemi-
cal Dynamics. Princeton University Press.
Simpson, T., Poplinski, J., Koch, P. N., and Allen, J. (2001).
Metamodels for computer-based engineering design:
Survey and recommendations. Eng. Comput., 17:129–
150. 10.1007/PL00007198.
Smola, A. J. and Sch¨olkopf, B. (2004). A tutorial on sup-
port vector regression. Stat. Comput., 14:199–222.
10.1023/B:STCO.0000035301.49549.88.
Søndergaard, J. (2003). Optimization using surrogate mod-
els - by the space mapping technique. PhD the-
sis, Informatics and Mathematical Modelling, Techni-
cal University of Denmark, DTU, Richard Petersens
Plads, Building 321, DK-2800 Kgs. Lyngby. Supervi-
sor: Kaj Madsen.
Tarantola, A. (2005). Inverse Problem Theory and Methods
for Model Parameter Estimation. SIAM.
IMPROVED SURROGATE-BASED OPTIMIZATION OF A MARINE ECOSYSTEM MODEL USING RESPONSE
CORRECTION
457
