
AGENT-BASED SIMULATION OF MOLECULAR PROCESSES
An Application to Actin-polymerisation
Stefan Pauleweit
Institute of Computer Science, Dept. of Systems Biology & Bioinformatics, University of Rostock, 18051 Rostock, Germany
J. Barbara Nebe
Center for Biomedical Research, Dept. of Cell Biology, University of Rostock, 18057 Rostock, Germany
Olaf Wolkenhauer
Institute of Computer Science, Dept. of Systems Biology & Bioinformatics, University of Rostock, 18051 Rostock, Germany
Keywords:
Agent-based model, Actin polymerisation, Arp2/3, Systems biology.
Abstract:
Agent-based modelling is widely used in ecology, economics and the social sciences. For the life science it
is an increasingly used technology. Here we use agent-based modelling to simulate the formation of actin
filaments, which is a major part in the cytoskeleton of the cell and plays a role in a number of cell functions.
We present in this paper three models with different levels of detail and show the potential of agent-based
models in systems biology by comparing the simulations to already published results.
1 INTRODUCTION
Agent-based simulations are a promising application
emerging in life sciences (Merelli et al., 2007). Ap-
plications of agent-based technologies in systems bi-
ology include studies in which each cell is modelled
as an agent (Thorne et al., 2007). Examples include
bacterial chemotaxis (Emonet et al., 2005), the phe-
nomenon where cells direct their movements in re-
sponse to external signals, models of epidermal tissue
(Grabe and Neuber, 2005), the formation of a 3D skin
epithelium (Sun et al., 2009) or a hybrid model, and
combination of agent-based simulations and differen-
tial equations to analyse the cell response to epider-
mal growth factors (Walker et al., 2006). Moreover,
agent-based models for intracellular interactions rep-
resenting the carbohydrate oxidation cell metabolism
(Corradini et al., 2005), the cell cycle (S¨utterlin et al.,
2009), the NF-κB signalling pathway (Pogson et al.,
2008) and molecular self-organisation, with the focus
on packing rigid molecules (Troisi et al., 2005), have
been proposed.
Actin polymerisation is a molecular process that
generates long filaments with a barbed and a pointed
end from single actin molecules that become part of
the cytoskeleton. The cytoskeleton provides the phys-
ical structure and shape of cells, as well as plays
an important role in a number of cell functions, in-
cluding cell motility (Cooper, 1991; Pantaloni et al.,
2001), endocytosis (Galletta et al., 2010), or cell
division (Pelham and Chang, 2002). Understand-
ing of actin organisation has important implications
for practical medical applications, including the de-
velopment of new topographies for implant surfaces
(Matschegewski et al., 2010; Nebe et al., 2007).
Here we focus on the spatial and time dependent
simulation of actin polymerisation. The literature de-
scribes a number of models analysing the cell motil-
ity driven by actin filaments, using partial differen-
tial equations (Mogilner and Edelstein-Keshet, 2002).
Another study used Brownian dynamics to analyse
the self-assembly process of actin and the dynamics
of long filaments (Guo et al., 2009). The distribution
of the length of actin filaments inside a cell was anal-
ysed with a discrete and continuous model (Edelstein-
Keshet and Ermentrout, 1998). Different models us-
ing stochastic Π-calculus as a representative of pro-
cess algebra, have also been published (Cardelli et al.,
2009).
In this paper we describe simulations using
276
Pauleweit S., Barbara Nebe J. and Wolkenhauer O..
AGENT-BASED SIMULATION OF MOLECULAR PROCESSES - An Application to Actin-polymerisation.
DOI: 10.5220/0003599702760282
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
276-282
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
an agent-based approach with communicating X-
machines (Gheorghe et al., 2005), implemented in
a software called Flexible Large-scale Agent-based
Modelling Environment (FLAME) (Kiran et al.,
2008). This allows us to analyse the spatial and time
dependent behaviour during the composition of the
filament structure by free actin with a high degree of
physical realism. The outline of the paper is as fol-
lows. Section 2 explains the three models in detail.
Section 3 discusses the output of the models and Sec-
tion 4 sums up the conclusions and gives a brief out-
look for further studies.
2 AGENT-BASED SIMULATION
An agent is formally defined as an finite-state ma-
chine. Because the finite-state machine model is
too restrictive for general system specification, an
extension with a memory, the so called X-machine
promise a better implementation (Holcombe, 1988).
If a system contains more than one agent, the par-
ticular X-machines must be able to communicate to-
gether and this leads to a communication X-machine
system (Gheorghe et al., 2005). This concept is im-
plemented in the software named Flexible Large-scale
Agent-based Modelling Environment (FLAME) (Ki-
ran et al., 2008).
Using the actin model generated by X-ray analysis
(Oda et al., 2009) we fix the size of one molecule to
50
˚
A×50
˚
A. The dimension of the molecule is shown
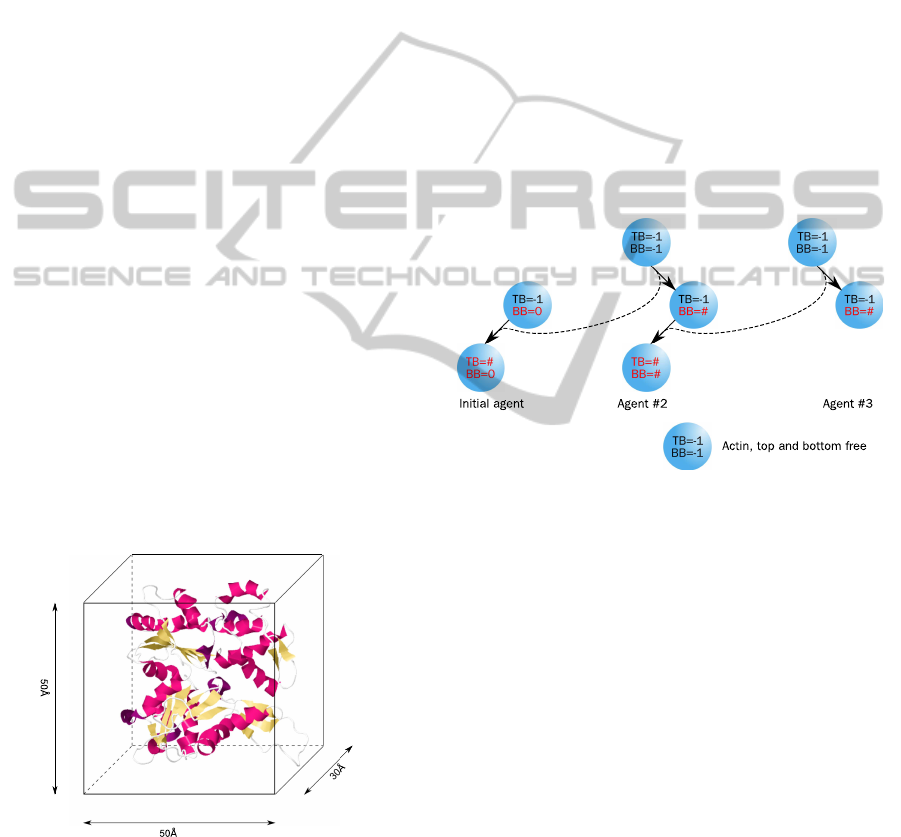
in Figure 1. Each agent contains an identification
Figure 1: The physical size of the actin molecule determines
the size of an agent in the simulation. For the two dimen-
sional simulation the width and height of an actin agent is
set to 50
˚
A×50
˚
A (Oda et al., 2009).
number and two binding sides to connect to another
agent, namely bottom-bound (BB) and top-bound
(TB) and can switch between three different states
(free, bottom-bound, fully bound). A free binding
side is denoted with the constant −1. As long as both
binding sides are marked with −1 (free), the agent is
randomly rotating and moving around in a distance of
1–200
˚
A, which is an approximation for the compu-
tational expensive calculation of Brownian dynamics.
If a molecule binds to another, then the identification
number of the counterpart is stored in the BB (respec-
tively TB) variable; the agent becomes immobilised
and its rotation will be adapted. The precondition for
binding is, that one of the agents is already bound
(bottom-bound). This leads to the condition that at
least one agent has to be stuck in the beginning of
the simulation. This is done by initialising one agent
with BB = 0. If a free agent binds to an already bound
one, the second becomes then fully bound (BB 6= −1,
TB 6= −1). The whole schema of the actin–actin in-
teractions is also shown in Figure 2. The polymerisa-
Figure 2: An actin-agent can be in three different states.
A free molecule can bind to an already bound initial agent
(BB = 0). The already bound actin-agent then become fully
bound. Then the third actin-agent can bind to the second
actin-agent which become fully bound and so on.
tion of actin filaments is characterised by a 70
◦
an-
gle branching on several positions mediated by the
Arp2/3 protein (Stossel et al., 2006). To simulate this
branching process, a new agent with a third binding
side was implemented. The orientation of the branch-
ing side to the left or right was set randomly. This
agent is restricted to bind only to actin-agents, so that
a Arp2/3-Arp2/3 combination is prohibited. In Figure
3 the scheme for the interactions and state changes is
illustrated. Similar to the actin-agent, the size of this
agent was determined from published measurements
(Robinson et al., 2001). Figure 4 shows the approxi-
mated dimensions of Arp2/3. An agent-based model
has to include the reaction kinetic in a reasonable way.
Due to the nature of spatial simulations with individ-
ual molecules, this may be done by an interaction vol-
ume, which defines a reaction zone around a particu-
lar agent (see Figure 5). Andrews and Bray (2004)
AGENT-BASED SIMULATION OF MOLECULAR PROCESSES - An Application to Actin-polymerisation
277

Figure 3: In addition to the actin-agent (Figure 2), the simu-
lation was extended with a second type of agent for Arp2/3.
This agent can bind to an bottom-bound actin-agent. Then
another actin-agent can bind to the top-binding side of the
Arp2/3-agent, the next actin-agent to the middle binding
side and the Arp2/3-agent becomes fully bound.
Figure 4: The physical size of Arp2/3 determines the size
of the agents in the simulation (Robinson et al., 2001).
Figure 5: The interaction boundary (dashed circle) defines
the reaction volume around an agent. If a second agent en-
ters this area, the reaction takes place.
developed an algorithm to determine this volume, but
considered more detailed interactions. Another way
is described by Pogson et al. (2006) where the inter-
action radius r is calculated by:
r =
3
r
3k∆t
4πN
A
10
3
where k is the kinetic rate constant, ∆t the discrete
time interval and N
A
is Avogadro’s constant (6.022×
10
23
). The rate constant for actin-actin assembly was
determined with 11.6µM
−1
s
−1
(Fujiwara et al., 2007)
and leads to a radius of 0.166
˚
A for ∆t = 1s. If two
or more agents enter the interaction volume at the
same time step, the closest molecule to the reaction
molecule assembles to it, if two or more have the same
distance, one will be chosen by chance.
To compare our results with the simulation of
Cardelli et al. (2009), we used the same number of
1200 free actin agents and 30 Arp2/3 agents. Cardelli
uses this number of agents to simulate a concentration
of 1200 µM. For concentration values in a spatial sim-
ulations, it is necessary to calculate the volume of the
environment:
n
Actin
= N
A
×V × c [1/mol × l × mol/l]
V = 1200/(N
A
· 1200× 10
−6
)
V = 1.66× 10
−18
l = 1.66× 10
−21
m
3
,
where n
Actin
is the number of molecules, N
A
is
again Avogadro’s constant, c is the concentration of
molecules and V is the volume. Assuming the envi-
ronment as a cube, the length of a side is approxi-
mately 1184.0
˚
A.
For a simulation including the dissolving of actin
from a filament, we used the rate constant of 5.4 s
−1
for ADP-actin at the barbed end from the literature
(Fujiwara et al., 2007). Only agents with a free top-
bound (in case of Arp2/3 also middle bound) can be
released from the filament. To avoid an instant re-
coupling, the molecule will be moved to outside the
interaction boundary.
Our present agent-based simulation takes place in
a 2D environment, so that we have to introduce a fac-
toring constant of 100 for the radius, the dissolving
rate constant and the size of the environment, follow-
ing the paper of Cardelli et al. (2009).
3 RESULTS
3.1 Actin-Actin Interactions
Figure 6 shows the time plot of the growth of one fil-
ament. The curve shows in the beginning a linear in-
crease (see inset of Figure 6), but later becomes loga-
rithmic. After 390 seconds 50 agents were integrated
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
278

in the filament, which corresponds to a filament of
length 0.25µm. A length of 1µm is reached after 1882
seconds and at the end of one hour, 240 agents form
a filament with a length of 1.2µm. In agreement with
Figure 6: The time plot shows the result of the simulation
for a simple actin polymerisation with 1200 agents and a
time step ∆t = 1s. Inset: Linear slope of the binding process
in the beginning.
published measurements (Fujiwara et al., 2007), the
increase in length of actin is linear in the beginning
of the simulation. The logarithmic curve on can be
explained by the decreased number of free molecules
and the spatial phenomena, by which the simulated
filament is growing close to the boundary of the en-
vironment. The number of reachable free molecules
close to this boundary is then much lower. The dif-
ference in the speed of elongation is related to two
reasons:
1. Actin filaments can growth on both side, whereas
the simulation allows only the growth at the
barbed end.
2. Actin can build small motile fragments, which
then elongate the filament (Stossel et al., 2006).
This increases the speed of polymerisation signif-
icantly.
3.2 Branching Process
Adding a new agent for the Arp2/3 protein, we simu-
lated the actin polymerisation with the branching pro-
cess. To visualise this, Figure 7 shows a snapshot
of the spatial distribution at the end of one hour. In
this simulation an overall filament length of 1µm was
reached after 578 seconds. At the end of one hour,
nearly all agents were involved in the filament struc-
ture, 1121 actin agents were fully bound. Addition-
ally 28 Arp2/3 agents are fully bound, two of them
Figure 7: The figure (cropped for better illustration) shows
the end result of the simulation for one hour with 1200
actin-agents and 30 Arp2/3-agents. The black points mimic
the free actin, the blue the agents bind to the filamental
structure.
Figure 8: The time plot shows the result of the branching
simulation for actin of 1200 actin-agents, 30 Arp2/3-agents
and a time step ∆t = 1s.
had an open binding side. Figures 8 and 9 show
the time plots for the actin and arp agents respec-
tively. Both time curves are sigmoidal with an inflec-
tion point around 1300 seconds.
In contrast to the filament formation, solely with
actin, the branching process accelerate the elongation
significantly. The snapshot in Figure 7 shows the spa-
tial consideration and is in good agreement with pre-
viously published simulations (Cardelli et al., 2009,
Figure 17).
3.3 Disassembly Process
To model the disassembly of actin and Arp2/3
molecules from the filamental structure, we added a
AGENT-BASED SIMULATION OF MOLECULAR PROCESSES - An Application to Actin-polymerisation
279
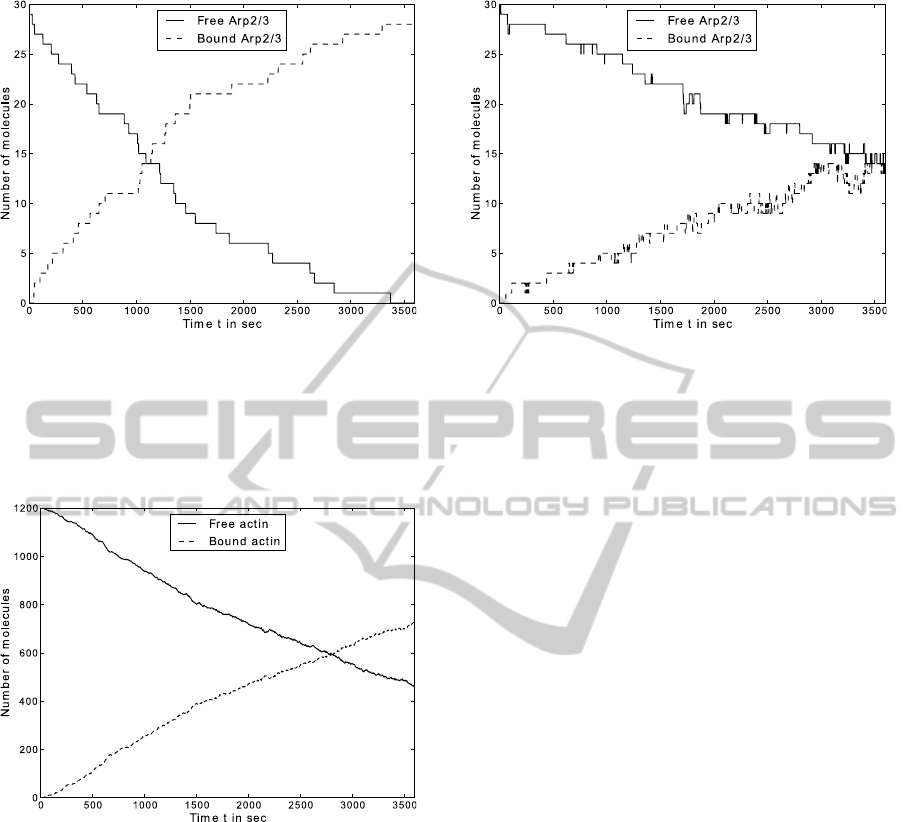
Figure 9: The time plot shows the result of the branching
simulation for Arp2/3 with 1200 actin agents, 30 Arp2/3
agents and a time step ∆t = 1s.
new probability for each agent.
After introducing this new variable, the assembly of
Figure 10: The time plot shows the result of the branching
simulation, including the disassembly process, for actin of
1200 actin-agents, 30 Arp2/3-agents and a time step ∆t =
1s.
the actin filament slowed down. As shown in Fig-
ure 10, the assembly of 200 molecules and therefore
an overall length of 1µm is reached after 760 sec-
onds. After one hour, the filament contained 717 fully
bounded actin-agents and is branched out at 14 differ-
ent positions (see also Figure 11). This model shows
therefore a comparable time progression to the simu-
lation of Cardelli et al. (2009) , especially for Arp2/3,
although our filamental growth is somewhat slower.
Figure 11: The time plot shows the result of the branching
simulation, including the disassembly process, for actin of
1200 actin-agents, 30 Arp2/3-agents and a time step ∆t =
1s.
4 CONCLUSIONS AND
OUTLOOK
Instead of the commonly used rate equations to simu-
late intracellular molecular processes, we introduced
an agent-based approach. This allowed us to over-
come some restrictions imposed by differential equa-
tion models, more precisely any number and any dis-
tribution, as well as spatial behaviour of molecules
can be easily modelled. Our model simulates actin
polymerisation, an important key player for different
cell functions.
The spatial outcome of our model is compara-
ble to alternative models of Cardelli et al. (2009), us-
ing the stochastic Π-calculus. Because the FLAME-
frameworkproduces XML-files for each time step, we
are also able to create an animated version for track-
ing the filament formation (not shown here). Addi-
tionally a time dependent analysis of the behaviour of
the single molecules and the filaments can be done.
The limit in using the agent-based approach is only
given by computational purposes.
Our overall aim is the development of a biophysi-
cal realistic model for actin polymerisation in human
cells. The advantage of our approach is the possibil-
ity to to extend the simulation to a massive number
of molecules with the aid of the parallelised FLAME
software version and, more important, the easy imple-
mentation of external influences. This should enable
us to analyse observed phenomena of actin cluster-
ing on titan pillar surface structures (Matschegewski
et al., 2010) with applications to implant technolo-
gies. This interesting issue makes it necessary to in-
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
280

clude more proteins like capping proteins which stop
the elongation of the filament (Pollard and Cooper,
1986).
ACKNOWLEDGEMENTS
We are grateful for financial support of the research
training school “Welisa”, which is founded by the
German Research Foundation (DFG 1505/1). Fur-
thermore the authors are thankful for the helpful ad-
vice of Prof. Mike Holcombe and Mark Burkitt from
the University of Sheffield.
REFERENCES
Andrews, S. S. and Bray, D. (2004). Stochastic simulation
of chemical reactions with spatial resolution and sin-
gle molecule detail. Phys. Biol., 1(3-4):137–151.
Cardelli, L., Caron, E., Gardner, P., Kahramano˘gulları, O.,
and Phillips, A. (2009). A process model of actin
polymerisation. Electronic Notes in Theoretical Com-
puter Science, 229(1):127–144. Proceedings of the
Second Workshop From Biology to Concurrency and
Back (FBTC 2008).
Cooper, J. A. (1991). The role of actin polymerization in
cell motility. Annu. Rev. Physiol., 53:585–605.
Corradini, F., Merelli, E., and Vita, M. (2005). A multi-
agent system for modelling carbohydrate oxidation in
cell. In Gervasi, O., Gavrilova, M., Kumar, V., La-
gan`a, A., Lee, H., Mun, Y., Taniar, D., and Tan, C.,
editors, Computational Science and Its Applications –
ICCSA 2005, volume 3481 of Lecture Notes in Com-
puter Science, pages 227–247. Springer Berlin / Hei-
delberg.
Edelstein-Keshet, L. and Ermentrout, G. B. (1998). Models
for the length distributions of actin filaments: I. simple
polymerization and fragmentation. Bull. Math. Biol.,
60(3):449–475.
Emonet, T., Macal, C. M., North, M. J., Wickersham, C. E.,
and Cluzel, P. (2005). Agentcell: a digital single-
cell assay for bacterial chemotaxis. Bioinformatics,
21(11):2714–2721.
Fujiwara, I., Vavylonis, D., and Pollard, T. D. (2007). Poly-
merization kinetics of adp- and adp-pi-actin deter-
mined by fluorescence microscopy. Proc. Natl. Acad.
Sci. U. S. A., 104(21):8827–8832.
Galletta, B. J., Mooren, O. L., and Cooper, J. A. (2010).
Actin dynamics and endocytosis in yeast and mam-
mals. Curr. Opin. Biotechnol., in Press.
Gheorghe, M., Stamatopoulou, I., Holcombe, M., and Ke-
falas, P. (2005). Modelling dynamically organised
colonies of bio-entities. In Banˆatre, J.-P., Fradet,
P., Giavitto, J.-L., and Michel, O., editors, Uncon-
ventional Programming Paradigms, volume 3566 of
Lecture Notes in Computer Science, pages 207–224.
Springer Berlin / Heidelberg.
Grabe, N. and Neuber, K. (2005). A multicellular systems
biology model predicts epidermal morphology, kinet-
ics and ca2+ flow. Bioinformatics, 21(17):3541–3547.
Guo, K., Shillcock, J., and Lipowsky, R. (2009). Self-
assembly of actin monomers into long filaments:
Brownian dynamics simulations. J. Chem. Phys.,
131(1):015102.
Holcombe, M. (1988). X-machines as a basis for dynamic
system specification. Softw. Eng. J., 3(2):69–76.
Kiran, M., Coakley, S., Walkinshaw, N., McMinn, P., and
Holcombe, M. (2008). Validation and discovery from
computational biology models. Biosystems, 93(1-
2):141–150.
Matschegewski, C., Staehlke, S., Loeffler, R., Lange, R.,
Chai, F., Kern, D. P., Beck, U., and Nebe, B. J. (2010).
Cell architecture-cell function dependencies on tita-
nium arrays with regular geometry. Biomaterials,
31(22):5729–5740.
Merelli, E., Armano, G., Cannata, N., Corradini, F.,
d’Inverno, M., Doms, A., Lord, P., Martin, A., Mi-
lanesi, L., M¨oller, S., Schroeder, M., and Luck, M.
(2007). Agents in bioinformatics, computational and
systems biology. Brief. Bioinform., 8(1):45–59.
Mogilner, A. and Edelstein-Keshet, L. (2002). Regulation
of actin dynamics in rapidly moving cells: a quantita-
tive analysis. Biophys. J., 83(3):1237–1258.
Nebe, J. G. B., Luethen, F., Lange, R., and Beck, U. (2007).
Interface interactions of osteoblasts with structured ti-
tanium and the correlation between physicochemical
characteristics and cell biological parameters. Macro-
mol. Biosci., 7(5):567–578.
Oda, T., Iwasa, M., Aihara, T., Ma´eda, Y., and Narita, A.
(2009). The nature of the globular- to fibrous-actin
transition. Nature, 457(7228):441–445.
Pantaloni, D., Clainche, C. L., and Carlier, M. F.
(2001). Mechanism of actin-based motility. Science,
292(5521):1502–1506.
Pelham, R. J. and Chang, F. (2002). Actin dynamics in
the contractile ring during cytokinesis in fission yeast.
Nature, 419(6902):82–86.
Pogson, M., Holcombe, M., Smallwood, R., and Qwarn-
strom, E. (2008). Introducing spatial information into
predictive nf-kappab modelling–an agent-based ap-
proach. PLoS One, 3(6):e2367.
Pogson, M., Smallwood, R., Qwarnstrom, E., and Hol-
combe, M. (2006). Formal agent-based modelling
of intracellular chemical interactions. Biosystems,
85(1):37–45.
Pollard, T. D. and Cooper, J. A. (1986). Actin and actin-
binding proteins. a critical evaluation of mechanisms
and functions. Annu. Rev. Biochem., 55:987–1035.
Robinson, R. C., Turbedsky, K., Kaiser, D. A., Marchand,
J. B., Higgs, H. N., Choe, S., and Pollard, T. D.
(2001). Crystal structure of arp2/3 complex. Science,
294(5547):1679–1684.
Stossel, T. P., Fenteany, G., and Hartwig, J. H. (2006).
Cell surface actin remodeling. J. Cell Sci., 119(Pt
16):3261–3264.
AGENT-BASED SIMULATION OF MOLECULAR PROCESSES - An Application to Actin-polymerisation
281

S¨utterlin, T., Huber, S., Dickhaus, H., and Grabe, N. (2009).
Modeling multi-cellular behavior in epidermal tissue
homeostasis via finite state machines in multi-agent
systems. Bioinformatics, 25(16):2057–2063.
Sun, T., Adra, S., Smallwood, R., Holcombe, M., and Mac-
Neil, S. (2009). Exploring hypotheses of the actions of
tgf-beta1 in epidermal wound healing using a 3d com-
putational multiscale model of the human epidermis.
PLoS One, 4(12):e8515.
Thorne, B. C., Bailey, A. M., and Peirce, S. M. (2007).
Combining experiments with multi-cell agent-based
modeling to study biological tissue patterning. Brief.
Bioinform., 8(4):245–257.
Troisi, A., Wong, V., and Ratner, M. A. (2005). An
agent-based approach for modeling molecular self-
organization. Proc. Natl. Acad. Sci. USA, 102(2):255–
260.
Walker, D., Wood, S., Southgate, J., Holcombe, M.,
and Smallwood, R. (2006). An integrated agent-
mathematical model of the effect of intercellular sig-
nalling via the epidermal growth factor receptor on
cell proliferation. J. Theor. Biol., 242(3):774–789.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
282
