
A FUZZY-PI CONTROLLER FOR WIND TURBINE DRIVEN DFIG
OPTIMIZED USING GENETIC ALGORITHMS
Lawrence K. Letting
1
, Josiah L. Munda
1
and Yskandar Hamam
1,2
1
Tshwane University of Technology, Pretoria, South Africa
2
ESIEE-Paris, Paris-Est University, LISV, UVSQ, Paris, France
Keywords:
DFIG, Fuzzy-PI control, Optimization, Genetic algorithms.
Abstract:
This paper presents the design of optimal TSK-fuzzy PI controller for the rotor side converter (RSC) of a
doubly fed induction generator (DFIG) in a grid connected wind generation system. The optimization strategy
is based on binary genetic algorithms. The controller is used to regulate the active and reactive power and hence
extract maximum energy from the system under varying wind speeds. Pitch angle control is used to regulate
the rotor angular speed while the active and reactive power are controlled by the rotor voltage supplied by the
RSC. The stator flux oriented reference frame is adopted. A fuzzy-PI controller with a minimum rule base
of nine rules is realized. The controller is implemented in C code as a dynamic linked library and simulated
using LabVIEW. Simulation results are presented.
1 INTRODUCTION
Wind energy is the fastest growing and the most
promising renewable energy source in the world to-
day. It is non-polluting, free and economically vi-
able. In addition, there has been a rapid technological
development in wind turbine technology (Munteanu
et al., 2008). In the recent past there has been an in-
creased use of DFIG’s in small power plants due to
their unique capabilities (Abedi et al., 2010). The
special features of DFIG are: it can supply power
at constant voltage and frequency; the rotor can op-
erate in both sub-synchronous or super-synchronous
speeds; the rating of the power converter is approxi-
mately 30% of the rated wind turbine power and; the
generated active and reactive power can be indepen-
dently controlled (Abo-Khalil et al., 2007).
To ensure maximum utilization of wind energy
in variable speed power plants, the stator active and
reactive power are controlled separately by varying
the rotor current of the DFIG using a vector control
scheme. A power converteris used to control the rotor
voltage. The control of power converters connected to
the DFIG is traditionally accomplished using propor-
tional and integral (PI) controllers. However, wind
energy conversion systems (WECS) are highly non-
linear with time-varying system parameters such as
wind speed and reference power values. This makes
it difficult to design optimal PI-controller gains using
either modern or classical control theory (Abedi et al.,
2010).
Artificial intelligence based methods using ge-
netic algorithms, particle swarm optimization (PSO),
and fuzzy logic have been introduced in order to im-
prove controller performance in WECS (Elshafei and
Azzouz, 2011), (Lin et al., 2011), (Ren et al., 2009),
(Leite et al., 2009), (Vieira et al., 2008). (Lin et al.,
2011) presents a particle swarm optimized recurrent
fuzzy neural network used to track the maximum
wind energy with reference values obtained from an
adaptive model reference observer. In (Leite et al.,
2009) PI controller gains are tuned using PSO with
aim of improving DFIG performance under network
faults. (Vieira et al., 2008) optimizes the PI-controller
gains using genetic algorithms in order to improve
active power control and dc-link voltage regulation.
(Ren et al., 2009) presents a 49-rule fuzzy controller
used to control the rotor speed and is shown to give
better performance than PI-control. (Elshafei and Az-
zouz, 2011) reports the design of a 9-rule adaptive
fuzzy controller (AFLC) for regulating the dc-link
voltage. The AFLC is shown to give better perfor-
mance compared to a classical PI controller and a 9-
rule non-adaptive FLC. It has therefore been estab-
lished that fuzzy control offers a great potential in
control of WECS.
This paper proposes an automated strategy for
tuning two fuzzy controllers used in regulation of ac-
348
K. Letting L., L. Munda J. and Hamam Y..
A FUZZY-PI CONTROLLER FOR WIND TURBINE DRIVEN DFIG OPTIMIZED USING GENETIC ALGORITHMS.
DOI: 10.5220/0003601403480353
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
348-353
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

tive and reactive power in the rotor side converter of
WECS. The FLCs are based on the first order Takagi-
Sugeno-Kang (TSK) model with two inputs: error
and integral of error. This proposed method shows
that it is possible to optimize a fuzzy-PI controller and
meet the desired performance with a minimum rule
base of only 9 rules. An optimized fuzzy-PI controller
gives performance similar to a classical PI controller
with adaptive gains.
2 SYSTEM CONFIGURATION
The system is configured as shown in Fig. 1. The
stator of the induction machine is directly connected
to the three- phase grid while the rotor winding is
supplied through the back-to-back converters. The
system is implemented with PI control in LabVIEW
control design and simulation module (NI LabVIEW,
2009). A master controller is used to regulate the ro-
tor angular speed by varying the pitch angle in order
to the ensure operation is maintained at an optimal
tip-speed ratio. The generator controller uses PI con-
trollers to regulate the active and reactive power. Vec-
tor control scheme is applied using the stator flux ori-
ented reference frame (Pena et al., 1996). The dc-link
voltage is fixed while the rotor side converter is mod-
eled as a voltage source. Grid-side converter control
is therefore not considered.
(NI LabVIEW, 2009) presents a WECS control
system model where the rotor-side converter regulates
the the stator active and reactive power through rotor
voltage components V
qr
and V
dr
which are indepen-
dently controlled by PI controllers. In this paper the
same model is adopted and the PI controllers are re-
placed by two fuzzy-PI controllers as shown in Fig.
2. FLC1 controls the rotor d-axis voltage while FLC2
controls the q-axis voltage. The two fuzzy controller
outputs V
∗
dr
and V
∗
qr
are used as the reference values
for the PWM controller connected to the rotor side
converter.
Detailed modeling of the DFIG and the vector
control scheme is available in (Pena et al., 1996). The
modeling of the wind-turbine and calculation of the
maximum active power reference values can be found
in (NI LabVIEW, 2009).
3 fuzzyPI CONTROLLER
STRUCTURE
The structure of the fuzzy-PI controller is presented
in Fig. 3. It comprises of four parts: fuzzification,
Pitch angle
control
Pitch angle
control
Drive train
Wind
DFIG
DC
AC
AC
DC
Grid
Converter control
Rotor side
converter
Grid side
converter
Figure 1: DFIG wind turbine configuration.
Calculation of
rotor current
reference values
_ _
,
s ref s ref
P Q
s
V
,
s r
I I
_
rq ref
I
_
rd ref
I
qr
I
dr
I
+
−
+
−
FLC1
1 /
s
FLC2
1 /
s
+
+
+
+
'
dr
V
'
qr
V
qr
V
∆
dr
V
∆
*
dr
V
*
qr
V
e
e
Figure 2: DFIG vector control scheme using fuzzy logic.
knowledge base, inference engine, and defuzzifica-
tion. There are two input variables, error e(t
k
), and
the integral of error ie(t
k
) at the k
th
simulation step
defined as:
e(t
k
) = i
ref
(t
k
) − i(t
k
) (1)
ie(t
k
) = e(t
k−1
) +
t
k
Z
t
k−1
e(t)dt (2)
where i
ref
(t
k
) and i(t
k
) are the reference and actual
values of the rotor dq-currents respectively.
The fuzzy control algorithm was developed in
C++ based on first order TSK-inference system. The
TSK fuzzy model is more compact with a computa-
tionally efficient representation than a Mamdani sys-
tem (Bose, 2002). The input membership functions
are encoded as shown in Fig. 4 using trapezoidal
membership functions. Each input is fuzzified using
three membership functions: Negative (N), Zero (Z),
and Positive(P). The FLC has nine rules and the out-
put of each rule is given by (3).
v(t
k
) = K
P
· e(t
k
) + K
I
· ie(t
k
) + K
0
(3)
Where K
P
, K
I
, and K
0
are constants to be determined
for each output MF in the inference engine of Fig. 3.
A FUZZY-PI CONTROLLER FOR WIND TURBINE DRIVEN DFIG OPTIMIZED USING GENETIC ALGORITHMS
349

e(k)
Inputs
Knowledge base
Fuzzification
interface
Inference engine
(decision making logic)
Defuzzification
interface
Output
ie(k)
N
Z
N
Z
P
1
MF
ie
e
P
2
MF
3
MF
4
MF
5
MF
6
MF
7
MF
8
MF
9
MF
Figure 3: Structure of the fuzzy-PI controller.
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
error (or integral of error)
Degree of membership
N Z P
x
4
x
3
x
2
x
1
Figure 4: Encoding of input membership functions.
4 OPTIMIZATION OF fuzzyPI
CONTROLLER
The conventional design of membership functions
and rule base of a fuzzy inference system is based on
expert knowledge. However, expert knowledge alone
is not enough to design a robust fuzzy controller for a
complex system such as WECS. In this design a fixed
rule base size and and input MF type were selected as
explained in section 3. The total number of variables
that need to be optimized for each FLC are summa-
rized in Table 1. The variable limits were identified by
performing initial simulation runs in open-loop mode.
Each FLC has 35 optimization variables.
During optimization using GA, each FLC is mod-
eled as single chromosome with 35 genes where each
gene represents a parameter in Table 1. The initial
Table 1: Optimization variables.
No.of
Parameter variables Min. Max.
e 4 −30 30
ie 4 −10 10
K
P
9 −1 1
K
I
9 −1 1
K
0
9 −1 1
Table 2: GA parameters.
Parameter Value
Population 70
Number of iterations 50
No. of bits 8
Selection rate 0.5
Mutation rate 0.2
population is randomly generated using the param-
eters of Table 2. At the end of each iteration the
cost of each chromosome is evaluated and ranking is
done. An elitist strategy is adopted such that 50%
of the individuals with the least cost are selected to
form the next population. The remaining members
are reproduced through mating of the selected indi-
viduals. Parents for mating are selected using rank-
weighting and the offspring is generated using single-
point crossover. Random mutations are carried out on
the population with a mutation rate of 20%. Muta-
tions ensure that the entire cost surface is explored.
The best chromosome is not mutated due to elitism.
The mean-square-error (MSE) defined in (4) and
(5) is used as the fitness function for FLC1 and FLC2
respectively. Equations (4) and (5) measure the devia-
tion from the desired reactive(Q) and active power(P)
respectively. The optimization variables for the two
fuzzy-PI’s are encoded in one matrix where each row
represents the parameters of FLC1 and FLC2 which
are used to run the system during one iteration. The
fitness of each row of the population is given by the
sum of the cost obtained in (4) and (5). Optimization
is carried out off-line before the start of the next iter-
ation. The simulation steps are illustrated in the the
flowchart of Fig. 5.
J
d
=
1
T
Z
(Q
ref
(t)− Q(t))
2
dt (4)
J
q
=
1
T
Z
(P
ref
(t)− P(t))
2
dt (5)
5 SIMULATION RESULTS
Optimal parameters for the fuzzy controllers is ob-
tained from the best chromosome at the end of the
simulation. The optimized input MFs for FLC1 and
FLC2 are presented Fig. 6 and Fig. 7 respectively.
The rule surface for FLC1 and FLC2 are shown in
Fig. 8 and Fig. 9 respectively. The contour maps are
shown at the bottom of each surface plot. The perfor-
mance of the fuzzy-PI was tested using the wind pro-
file of Fig.10. It is observedin Fig. 11 and Fig. 13 that
the proposed controller is able to track the maximum
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
350
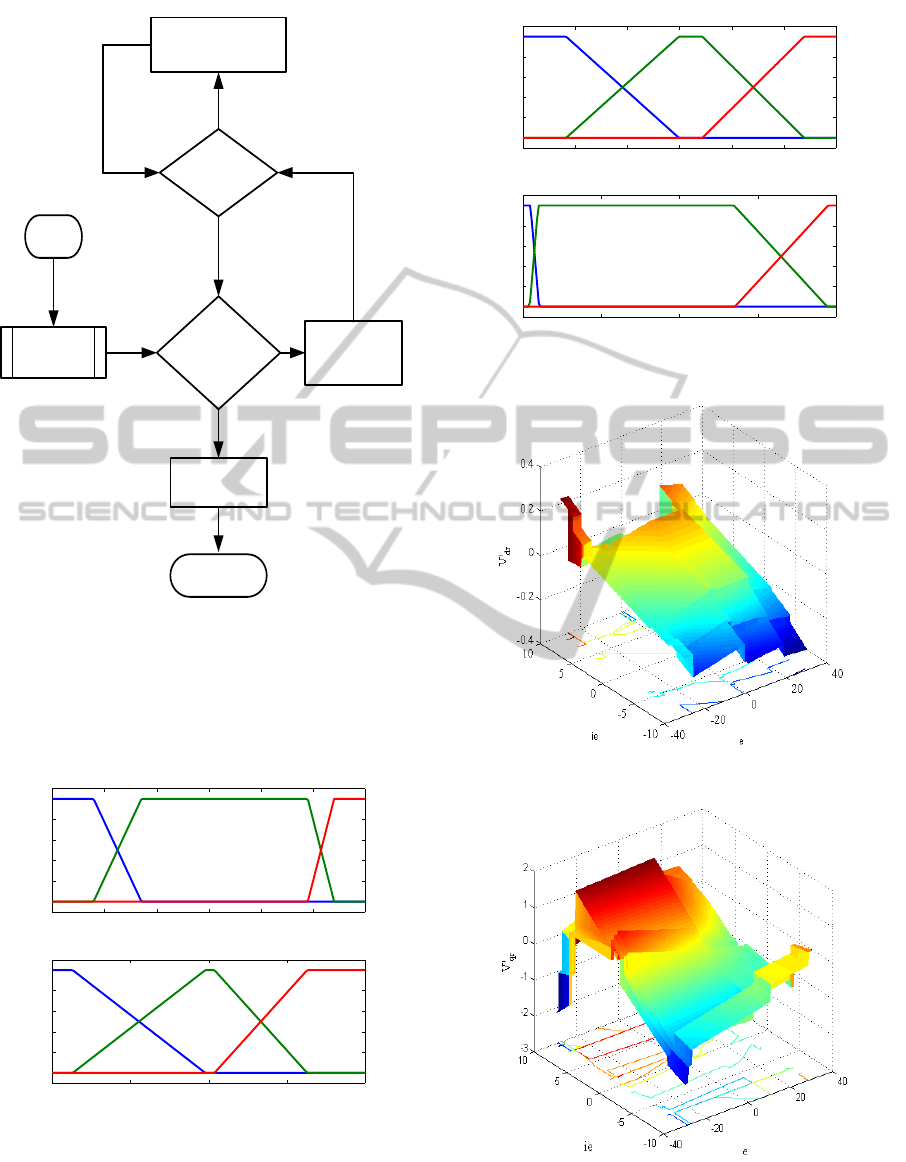
k>P?
(all FLCs
simulated?)
Simulate current FLC
and update cost,
Run genetic
algorithm
Max. no. of
iterations
reached?
Download results
to disk
Stop
Start
Initialization
Yes
No
Yes
No
Figure 5: Illustration of optimization procedure.
energy from the wind and maintain the stator reactive
power close to zero. The reference active power is
obtained from the rotor current q-axis reference com-
ponent (I
qr
ref
).
−30 −20 −10 0 10 20 30
0
0.2
0.4
0.6
0.8
1
e
Degree of membership
N Z P
−10 −5 0 5 10
0
0.2
0.4
0.6
0.8
1
ie
Degree of membership
N Z P
Figure 6: Optimized input MFs for FLC1.
−30 −20 −10 0 10 20 30
0
0.2
0.4
0.6
0.8
1
e
Degree of membership
N Z P
−10 −5 0 5 10
0
0.2
0.4
0.6
0.8
1
ie
Degree of membership
N Z P
Figure 7: Optimized input MFs for FLC2.
Figure 8: Optimized rule surface for FLC1.
Figure 9: Optimized rule surface for FLC2.
A FUZZY-PI CONTROLLER FOR WIND TURBINE DRIVEN DFIG OPTIMIZED USING GENETIC ALGORITHMS
351

Figure 10: Wind profile (base speed 12m/s).
Figure 11: DFIG active power (P
s
).
Figure 12: Control signal (V
′
q
).
Figure 13: DFIG reactive power (Q
s
).
6 CONCLUSIONS
In this paper an optimized fuzzy-PI controller for ac-
tive and reactive power control in the rotor side con-
Figure 14: Control signal (V
′
d
).
verter of a wind energy conversion system is pro-
posed. It is shown that it is possible to design and
optimize a fuzzy-PI controller with a minimum rule
base of nine rules using genetic algorithms. The ad-
vantage of the small rule base is that it requires less
memory space with faster execution speed. It is an
improvement from the standard fuzzy-PI controllers
with 49 rules. Comparison of the performance of the
proposed fuzzy-PI and other methods such as classi-
cal PI and PI with optimized gains is part of future
work.
REFERENCES
Abedi, A., Pishvaei, M., Madadi, A., and Kelk, H. M.
(2010). Analyzing vector control of a grid-connected
dfig under simultaneous changes of two inputs of con-
trol system. European Journal of Scientific Research,
45(2):221–231.
Abo-Khalil, A., Lee, D.-C., and Jang, J.-I. (2007). Con-
trol of back-to-back pwm converters for dfig wind tur-
bine systems under unbalanced grid voltage. In Indus-
trial Electronics, 2007. ISIE 2007. IEEE International
Symposium on, pages 2637 –2642.
Bose, B. K. (2002). Modern Power Electronics and AC
Drives. Prentice-Hall, Inc.
Elshafei, A. and Azzouz, M. (2011). Adaptive fuzzy regu-
lation of the dc-bus capacitor voltage in a wind energy
conversion system (wecs). Expert Systems with Appli-
cations, 38(5):5500 – 5506.
Leite, H., Barros, J., and Miranda, V. (2009). Evolutionary
algorithm epso helping doubly-fed induction genera-
tors in ride-through-fault. In PowerTech, 2009 IEEE
Bucharest, pages 1 –8.
Lin, W.-M., Hong, C.-M., and Cheng, F.-S. (2011). De-
sign of intelligent controllers for wind generation sys-
tem with sensorless maximum wind energy control.
Energy Conversion and Management, 52(2):1086 –
1096.
Munteanu, I., Bratcu, A. I., Cutululis, N.-A., and Ceangˇa,
E. (2008). Optimal Control of Wind Energy Systems,
Towards a Global Approach. Springer-Verlag, Lon-
don.
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
352

NI LabVIEW (2009). Designing controllers
for a doubly-fed wind power system.
http://zone.ni.com/devzone/cda/epd/p/id/6272.
Accessed: 1st April 2011:
http://zone.ni.com/devzone/cda/epd/p/id/6272.
Pena, R., Clare, J., and Asher, G. (1996). Doubly fed induc-
tion generator using back-to-back pwm converters and
its application to variable-speed wind-energy genera-
tion. Electric Power Applications, IEE Proceedings -,
143(3):231 –241.
Ren, Y., Li, H., Zhou, J., An, Z., Liu, J., Hu, H., and
Liu, H. (2009). Dynamic performance analysis of
grid-connected dfig based on fuzzy logic control. In
Mechatronics and Automation, 2009. ICMA 2009. In-
ternational Conference on, pages 719 –723.
Vieira, J., Nunes, M., and Bezerra, U. (2008). Design of
optimal pi controllers for doubly fed induction gen-
erators in wind turbines using genetic algorithm. In
Power and Energy Society General Meeting - Con-
version and Delivery of Electrical Energy in the 21st
Century, 2008 IEEE, pages 1 –7.
APPENDIX
The parameters of the DFIG are given in Table 3.
Table 3: DFIG Parameters.
Parameter Value
Power base 4.8MW
Frequency base 60Hz
Stator resistance 0.003068pu
Rotor resistance 0.006068pu
Rotor leakage inductance 0.05783pu
Stator leakage inductance 0.05783pu
Mutual inductance 1.85068pu
Gear box ratio 55
A FUZZY-PI CONTROLLER FOR WIND TURBINE DRIVEN DFIG OPTIMIZED USING GENETIC ALGORITHMS
353
