DGridSim: A REAL-TIME DATA GRID SIMULATOR WITH

HIERARCHICAL JOB AND DATA SCHEDULING

Safai Tandoğan

, Atakan Doğan

and Celal Murat Kandemir

C Tech, TUBITAK MAM TEKSEB, Kocaeli, Turkey

Department of Electrical and Electronics Engineering, Anadolu University, Eskisehir, Turkey

Department of Electrical and Electronics Engineering, Eskisehir Osmangazi University, Eskisehir, Turkey

Keywords: Discrete-event simulation, Modeling, Data Grid.

Abstract: In this study, DGridSim, a process oriented and discrete-event driven all-in-one Data Grid simulator, is

introduced, and some initial simulation results are reported to validate its operation. DGridSim has some

distinguishing features which make it unique among the Data Grid simulators available in the literature.

First of all, in order to provide the guaranteed service to real-time jobs running on the system, DGridSim

incorporates the advance reservation of all system resources, including computing, network, and storage.

Second, DGridSim supports a hierarchical real-time scheduling architecture for both jobs and jobs’ data.

Third, it allows the simulation of all related components of a Data Grid system which may have an impact

on the system’s real-time performance.

1 INTRODUCTION

In this study, a real-time Data Grid simulator,

namely DGridSim is presented. The main objective

in developing DGridSim is to provide an all-in-one

platform to study real-time job distribution, data

replication, and data dissemination algorithms for

Data Grids.

In the literature, a variety of simulators has been

proposed: Optorsim (Camaron, Millar, Nicholson,

Schiaffino, Zini and Stockinger, 2004), GridSim

(Buyya and Murshed, 2002, Sulistio, Cibej, Robic

and Buyya, 2008), SimGrid (Casanova, 2001). A

comparison study of a variety of simulators for the

Grid systems, including GridSim, Optorsim, and

SimGrid, was presented by Quetier and Cappello,

2005.

None of aforementioned simulators focuses on

the evaluation of the real-time performance of the

Grid systems. Furthermore, among these simulators,

DGridSim has some remarkable features, some of

which are as follows: (1) Hierarchical real-time job

scheduling algorithms can be simulated, where they

can run either online or offline mode. (2) Pull or

push based data replication algorithms can be

simulated. (3) A data dissemination algorithm can be

evaluated together with a data replication algorithm

and job scheduling algorithm, or vice versa. (4) The

network traffic model is based on the flows due to

the file transfers. All network resources are treated

as the first class entities similar to the computing and

storage resources. As a result, the network

connectivity is transformed into a scheduled service.

(5) Its design is modular, extensible and layered to

provide for the maximum flexibility in simulating

different Data Grid system scenarios.

2 DGridSim

DGridSim is written in C++ programming language

using C++SIM20 discrete-event simulator library by

Mesquite Software. The C++SIM20 library allows

the development of process-oriented discrete-event

simulation programs. A program using C++SIM20

library models a system as a collection of

C++SIM20 processes which interact with each other

by using the C++SIM20 structures. The C++SIM20

structures that are used in DGridSim are the

following: process, facility, and event.

DGridSim is a simulator that has been designed

to achieve modularity, extensibility, and layered

architecture. Specifically, the layered architecture

means that DGridSim is built in layers with respect

174

Tando

gan S., Do

gan A. and Murat Kandemir C..

DGridSim: A REAL-TIME DATA GRID SIMULATOR WITH HIERARCHICAL JOB AND DATA SCHEDULING.

DOI: 10.5220/0003601501740179

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages

174-179

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

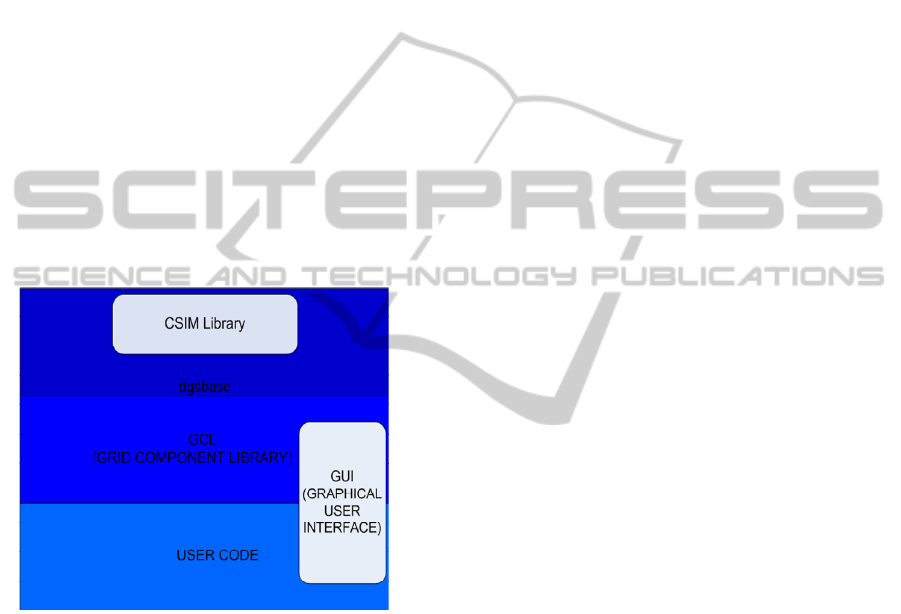
to the layered software architecture of real Grid

systems where the higher layers make use of the

functionalities provided by the lower layers.

DGridSim is composed of four layers: Basic Grid

Fabric, Communication, Main Grid Services, and

Applications. These layers as well as how advance

reservation mechanism is implemented for

computing, networking, and storage resources were

explained by Atanak, Tandogan and Doğan, 2010.

Note that without the advance reservation, it is

impossible to guarantee any form of quality of

service.

2.1 System Architecture

The system architecture of DGridSim is shown in

Figure 1. DGridSim is a layered software with a

well-defined object hierarchy. The hierarchy

between the objects is established using interfaces,

Abstract Base Classes in C++. This provides a

flexible and expandable environment for

researchers.

Figure 1: DGridSim system architecture.

At the bottom level, there exists CSIM. A Base

Layer containing low level simulation utilities, such

as registering events, advancing simulation time,

etc., has been developed using this CSIM

development kit. A Grid Component Library (GCL)

Layer defining interfaces and contracts for grid

services and grid models has been designed on this

Base Layer. The User Code Layer consists of the

standard and specialised implementations of the

interfaces defined in GCL Layer. A Graphical User

Interface Layer is planned for the future. The User

Code Layer is the layer for researchers to inject their

own implementations of different grid algorithms. If

predefined service contracts or grid models are not

adequate for the researcher, new interfaces should be

defined in GCL Layer. It is expected that no

intervention should be necessary to the Base Layer.

2.2 Service Architecture

Data Grid components can be divided into two main

groups, Resource Components and Service

Components. Resource Components do have

definite properties. For example, a Storage Element

can have properties such as storage space, read/write

bandwidth, and access latency, but do not have any

business logic (a Storage Element does not contain

any procedures). Since Resource Components are

passive components, Resource Managers are

required to perform necessary operations on them.

Following the CSIM terminology, Resource

Components are designed using facilities, and

Service Components are designed using processes.

Service Components can be based on three

different interfaces in DGridSim. Asynchronous

Service Base is designed to operate on a queue. This

queue can be a collection of grid jobs or data

transfer requests. Queue handling mechanism can be

triggered periodically or by a preconfigured event.

Scheduling Services are developed by extending

Asynchronous Service Base.

Synchronous Service Base provides its service

by simple function calls. Each function call can have

a cost which can be determined at run-time by

extending this base interface. Information Services

are usually developed on top of Synchronous

Service Base.

The third base is the combination of

Asynchronous and Synchronous Service Base and is

called as Hybrid Base. Hybrid Base controls a queue

and at the same time offers simple function calls.

Reservation Services are based on Hybrid Base

because they need to process the reservation requests

which are placed in a queue and also they need to

provide functions for committing or cancelling a

reservation request.

3 JOB SCHEDULING

DGridSim supports the simulation of hierarchical

Data Grid systems where a global scheduler (Grid

Scheduler) for the whole system and a local

scheduler (Site Scheduler) for each site are deployed

to manage the available computing resources.

3.1 Grid Scheduler

In DGridSim, all Grid schedulers are implemented



DGridSim: A REAL-TIME DATA GRID SIMULATOR WITH HIERARCHICAL JOB AND DATA SCHEDULING

175

as a part of Grid Scheduling Service (GSS). In order

to support the job scheduling activities, Grid

Scheduling Service interacts with some other global

services as follows:

1. Grid Job Submission Service (GJSS): GJSS

accepts the jobs submitted by the applications,

and invokes the scheduler.

2. Grid Job Dispatch Manager (GJDM): Once a

site has been determined for a job, GSS

informs GJDM for the submission of the job to

this site.

3. Grid Information Service (GIS): GIS provides

GSS (and Data Management Service) with all

sorts of static and dynamic information related

to the system.

4. Replica Location Service (RLS): RLS is

queried to find the physical location of all data

items available in the system.

3.1.1 Random

The Random algorithm is implemented as an online

algorithm in GSS as follows:

1. Once a new job is submitted to the system,

GJSS places it to a queue and invokes GSS.

2. GSS handles each job in the queue one by one.

For the current job, GSS randomly selects a

site and informs GJDM.

3. GJDM forwards the job to the selected site.

3.1.2 Earliest Deadline First

The Earliest Deadline First algorithm is realized as

an offline algorithm in GSS and it runs as follows:

1. Once a new job is submitted to the system,

GJSS places it to a queue. Then, different from

the online case, it invokes GSS periodically

with a predefined period.

2. Upon invoking, GSS handles all jobs in the

queue at the same time. GSS sorts the jobs in

the increasing value of deadline; randomly

selects a site in the sorted order for each job;

informs GJDM.

3. GJDM forwards the job to the selected site.

3.1.3 Minimum Completion Time First

The Minimum Completion Time First (MCTF)

algorithm is realized in GSS as follows:

1. When a new job is submitted to the system,

GJSS first places it to a queue. Then, it invokes

GSS immediately since MCTF is an online

algorithm.

2. GSS handles each job in the queue one by one.

For the current job, GSS sends an inquiry to

GIS to fetch p

(total computing power in

MIPS) and l

(average instantaneous computing

load in seconds) for all sites.

3. GSS computes the expected job finish times c

for each site, where c

= l

+ t

and t

is the

number of instructions of the current job.

4. GSS selects the site with minimum job

completion time and informs GJDM.

5. GJDM forwards the job to the selected site.

3.2 Site Scheduler

DGridSim realizes all site schedulers as a part of

Site Scheduling Service (SSS). In order for Site

Scheduling Service to carry out the job scheduling

activities, it cooperates with other local services as

follows:

1. Site Job Submission Service (SJSS): SJSS

accepts the jobs submitted by GJSS, and

invokes the site scheduler.

2. Site Job Invoke Manager (SJIM): Once a

scheduling decision has been made for a job,

SSS informs SJIM about this job as well as the

related information, such as the computing

element chosen, job start time and duration of

execution. SJIM simulates the execution of the

job by creating a CSIM process which uses the

CSIM facility for the chosen computing

element for the duration of execution starting

from the start time.

3. Local Reservation Service (LRS): LRS holds

all the advance reservations made for the

computing/storage/networking resources in the

site.

4. Local Data Manager (LDM): LDM is the

facade of Local Data Management Service,

which is explained in Section 4. Local Data

Management Service has the responsibility of

making data available for the jobs running in

the site. LDM can provide the requested data

from the local storage element, or from a

remote one with the help of global Data

Manager.

3.2.1 Real-time Min-max

DGridSim currently supports an online site

scheduling algorithm, namely real-time Min-max.

The operation of SSS with real-time Min-max is as

follows:

1. Once a new job is received by SJSS, SJSS

places it to a queue and invokes SSS.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

176

2. SSS handles each job in the queue one by one.

For the current job, SSS sends an inquiry to

LRS asking for a free time-slot on each

computing element, where the slot start time is

the current time and the slot finish time is the

task deadline.

3. Local Reservation Service returns the time slot

with the latest start time for each computing

machine. Thus, this is the max operation.

Among the time slots returned by LRS, SSS

selects the computing element with the earliest

start time, which is the min operation.

4. Once a deadline satisfying time-slot is found,

SSS submits a data transfer request for the

job’s data to Local Data Manager, where the

data request deadline is set to the start time of

the time-slot.

5. If LDMS guarantees that the requested data

will be copied into the site before the data

request deadline, SSS considers the job to be

satisfied, and invokes SJSS. Otherwise, SSS

drops the job from the queue.

6. Site Job Invoke Manager enables running the

job in the time-slot determined by the

scheduler on the chosen computing element.

4 DATA SCHEDULING

DGridSim realizes data scheduling in hierarchical

fashion similar to the job scheduling. That is, there is

a global Data Management Service (DMS) for the

whole system, and a Local Data Management

Service (LDMS) for each site.

4.1 Data Management Service

In the DGridSim, Data Management Service (DMS)

coordinates the transfer of data from one site to

another. In doing so, DMS cooperates with some

other services.

1. Data Manager (DM): DM is the service point

of DMS for all sites in the Grid. That is, all

Local Data Management Services use DM to

submit a site-to-site data transfer request to

DMS.

2. Reservation Service (RS): When DMS finds a

feasible path for a data transfer request by

means of a data dissemination algorithm, a

specific bandwidth value must be reserved on

all links of the path. Thus, DMS sends a

reservation request to RS so that RS can make

these bandwidth reservations on the respective

links.

3. File Transfer Service (FTS): After DMS is

informed by RS that all reservations are

successful, DMS starts FTS in order to copy a

data item from one site to another.

4.1.1 Minimum Delay Feasible Path First

Data Management Service runs a data dissemination

algorithm, namely Minimum Delay Feasible Path

First (MD/FPF), to find a feasible path for each data

request. A path is considered to be feasible if and

only if it has the sufficient bandwidth to deliver the

data to its destination at its deadline. DMS realizes

MD/FPF as follows.

1. Once a site-to-site data transfer request is

received by DM, DM puts it to a queue and

invokes DMS. Thus, DMS runs in online

mode.

2. DMS handles each request in the queue one by

one. For the current data request, DMS sends

an inquiry to Replica Location Service to find

out all source sites where the requested data

item is located.

3. DMS fetches the information about available

link bandwidths and network topology from

GIS.

4. DMS computes the required minimum

bandwidth value: bw = (file_size)/ (request _

deadline – current _ time). Based on the

undirected graph model of the system due to

the network topology, DMS deletes all links

with an available bandwidth value less than bw

from the graph.

5. In the modified graph, DMS runs the Dijkstra’s

shortest path algorithm to find out a minimum

delay feasible path.

6. After finding a path, DMS submits a

reservation request to Reservation Service

which includes all the links on the path,

reservation start (current time) and finish

(request deadline) times, and bandwidth value

(bw).

7. If all reservations are succeeded, DMS calls for

File Transfer Service to start the site-to-site

data transfer over the reserved path. Otherwise,

this request is deemed to be unsatisfiable. In

either case, Data Manager informs LDMS

accordingly.

4.2 Local Data Management Service

Local Data Management Service (LDMS) is

decoupled from Site Scheduling Service and it

coordinates the site’s data services as explained

DGridSim: A REAL-TIME DATA GRID SIMULATOR WITH HIERARCHICAL JOB AND DATA SCHEDULING

177

below.

1. While a job is being scheduled by SSS, SSS

places a data request to Local Data Manager,

which is the LDMS’s service point to SSS.

LDM puts this request in a queue and invokes

LDMS.

2. For the current data request, LDMS contacts

with Local Replica Location Service and learns

if the requested data item(s) can be locally

provided.

3. For the data items which are already available

in the site, LDMS submits a reservation request

to Local Reservation Service. This request

includes the all the links from a local storage

element to the chosen computing element,

reservation start (current time) and finish

(request deadline) times, and bandwidth value

(bw).

4. For the unfound data items, LDMS sends a

data request to Data Manager so that these

items can be copied from some remote site(s)

into this site.

5. If all local reservations are successfully made,

and/or LDMS is informed by Data Manager

that the requested data item(s) will be available

at the task start time, Local Data Manager

notifies SSS with either positive/negative

acknowledgement accordingly.

5 EXPERIMENTS

Using DGridSim, the three Grid scheduling

algorithms were evaluated. With the start of the

simulation, a Data Grid system was created. The

system was assumed to have the following

properties. It has ten sites each of which includes

thirty-two heterogeneous computing elements and a

single storage element. The computing elements

have MIPS rating of U~[7500, 12500], where U~

means uniformly distributed, and the storage

elements have storage capacity of U~[175000,

225000] Mbytes. Furthermore, every site is

equipped with a gateway router to which all

computing and storage elements are connected. The

links between computing and storage elements and

their gateway have bandwidth of U~[750, 1250]

Mbytes/sec and U~[1750, 2250] Mbytes/sec,

respectively. Ten gateway routers are interconnected

by a randomly generated network topology

composed of ten routers and twenty-five links whose

bandwidths with an average bandwidth of U~[750,

1250] Mbit/sec.

After the creation of a Data Grid system, jobs

were produced. The jobs were characterized with job

size, deadline, and the number of data items. In the

base set of simulation studies, job sizes are

U~[3750000, 7500000] MI (Million Instruction),

deadlines are U~[750, 1250] seconds, and the

number of data items needed in order for jobs to

start their execution is just one. During the

simulations, jobs were submitted to the system with

a rate of one job per five seconds.

Initially, all two-hundred different data items

were assumed to be stored in a single (Tier-0) site

without any computing elements. Thus, all data are

distributed from this Tier-0 site to all other sites with

computing capability. Moreover, jobs are randomly

associated with the data items whose sizes are

U~[750, 1250] Mbytes.

Using DGridSim, a base set of results was first

established for the following parameter values:

Number of Jobs=1000, Mean Job Size=5000000 MI,

Mean Job Deadline=100 sec, Mean Number of Data

Items=1 and Mean Link Bandwidth=125

Mbytes/sec. Later, these parameters are varied and

the effects are observed and reported in Tables 1-3.

Each data in Tables 1-3 denotes the average

satisfiability (the ratio of number of jobs finished

before their deadlines to total number of jobs) in

three simulation runs.

Table 1 shows the effect of changing the number

of jobs submitted to the system from 1000 to 3000

on the algorithms. According to Table 1, all three

algorithms maintain a relatively stable performance

on average. Furthermore, Random and EDF have

shown very similar performance, and they are

slightly better than MCTF.

Table 1: Performance of the three grid scheduling

algorithms when the number of jobs is increased.

Number of Jobs

1000 1500 2000 2500 3000

Random 0.94 0.96 0.96 0.97 0.98

EDF 0.94 0.96 0.96 0.97 0.98

MCTF 0.92 0.90 0.89 0.92 0.85

Table 2 shows the impact of increasing the mean

job size from 5000000 (5 M) MI to 1000000 (10 M)

MI on the algorithms. According to Table 2,

increasing job sizes significantly degrades the

performance of MCTF. On the other hand, it seems

that both Random and EDF keep its performance at

a top level.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

178

Table 2: Performance of the three grid scheduling

algorithms when the mean job size is increased.

Mean Job Size (MI)

5 M 6 M 7 M 8 M 10 M

Random 0.94 0.95 0.97 0.96 0.97

EDF 0.94 0.95 0.97 0.96 0.97

MCTF 0.92 0.90 0.67 0.50 0.33

Table 3 shows the impact of increasing the mean

job deadline from 600 sec to 1000 sec on the

algorithms. According to Table 3, increasing

deadline clearly helps MCTF to improve its

performance. On the other hand, neither Random nor

EDF has experienced a significant variation in their

performance.

Table 3: Performance of the three grid scheduling

algorithms when the mean deadline is increased.

Mean Job Deadline (sec)

600 700 800 900 1000

Random 0.96 0.97 0.98 0.98 0.97

EDF 0.96 0.97 0.97 0.98 0.97

MCTF 0.55 0.69 0.89 0.90 0.92

Because of the space constraints, the other

simulation results are not reported in detail here.

Yet, the following trends were observed in those

results. When the mean number of data items is

increased from 1 to 5, all three algorithms have

shown deteriorating performances. This is a

somewhat expected result. That is, jobs need more

than one data item to be copied to the sites where

they are scheduled. While keeping the network

resources at a fixed capacity, meeting the deadlines

of increasing number of data transfer requests under

stringent timing constraints is difficult to maintain.

When the mean link bandwidth is increased from

25 Mbytes/sec to 200 Mbytes/sec, all three

algorithms have shown increasing performances.

While keeping the deadlines close to some fixed

value, increasing the mean link bandwidths enables

that the data transfer times will get shorter. Thus,

jobs will get higher chance of meeting their

deadlines, as observed in the table.

6 CONCLUSIONS

This study presented a novel all-in-one real-time

Data Grid simulator supporting advance reservation

to test the real time performance of the job

scheduling and data dissemination algorithms in a

Data Grid system. The design of DGridSim provides

a flexible environment for researchers working on

real-time characteristics of Data Grid systems. It

should be emphasized that the presented results

prove the correct operation of DGridSim. The

development of DGridSim continues in several

avenues, including the support for centralized and

distributed Grid models, new heuristics for job and

data scheduling and data replication.

ACKNOWLEDGEMENTS

This material is based on work supported by

Institute of Scientific and Technological Research of

Turkey under Grant

No. 108E232.

REFERENCES

Camaron, D. G., Millar, A. P., Nicholson, C., Schiaffino,

R. C., Zini, F., Stockinger, K., 2004. Analysis of

Scheduling and Replica Optimisation Strategies for

Data Grids using OptorSim. Journal of Grid

Computing, 2(1), 57-69.

Buyya, R., Murshed, M., 2002. GridSim: A Toolkit for the

Modeling and Simulation of Distributed Resource

Management and Scheduling for Grid Computing. The

Journal of Concurrency and Computation: Practice

and Experience, 14, 13-15.

Sulistio, A., Cibej, U., Robic, B., Buyya, R., 2008. A

Tookit for Modeling and Simulation of Data Grids: An

Extension to GridSim. Concurrency and Computation:

Practice and Experience, 20(13), 1591-1609.

Casanova, H., 2001. SimGrid: A Toolkit for the

Simulation of Application Scheduling. IEEE Int’l

Symposium on Cluster Computing and the Grid, 430.

Quetier, B., Cappello, F., 2005. A Survey of Grid

Research Tools: Simulators, Emulators and Real Life

Platforms. 17th IMACS World Congress.

Atanak, M. M., Tandogan, S., Doğan., A., 2010. A

Unified Model for Real-time Data Grids Supporting

Hierarchical Scheduling of Jobs and Data. Int’l

Conference on Modelling, Simulation, and

Visualization Methods.

Mesquite Software, (n.d.). User’s Guide: CSIM20

Simulation Engine (C++ Version). Retrieved May 23,

2011, from http://www.mesquite.com.

DGridSim: A REAL-TIME DATA GRID SIMULATOR WITH HIERARCHICAL JOB AND DATA SCHEDULING

179